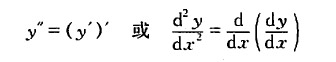粉丝日志

Posted:

Nov 16, 2014

Tags:

Comments:

R语言的导数计算

R的极客理想系列文章，涵盖了R的思想，使用，工具，创新等的一系列要点，以我个人的学习和体验去诠释R的强大。

R语言作为统计学一门语言，一直在小众领域闪耀着光芒。直到大数据的爆发，R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入，R语言的社区在迅速扩大成长。现在已不仅仅是统计领域，教育，银行，电商，互联网….都在使用R语言。

要成为有理想的极客，我们不能停留在语法上，要掌握牢固的数学，概率，统计知识，同时还要有创新精神，把R语言发挥到各个领域。让我们一起动起来吧，开始R的极客理想。

关于作者：

张丹(Conan), 程序员Java,R,PHP,Javascript
weibo：@Conan_Z
blog: http://blog.fens.me
email: bsspirit@gmail.com

转载请注明出处：
http://blog.fens.me/r-math-derivative/

$r-math-adv1$

前言

高等数学是每个大学生都要学习的一门数学基础课，同时也可能是考完试后最容易忘记的一门知识。
我在学习高数的时候绞尽脑汁，但始终都不知道为何而学。生活和工作基本用不到，就算是在计算机行业和金融行业，能直接用到高数的地方也少之又少，学术和实际应用真是相差太远了。

不过，R语言为我打开了一道高数应用的大门，R语言不仅能方便地实现高等数学的计算，还可以很容易地把一篇论文中的高数公式应用于产品的实践中。
因为R语言我重新学习了高数，让生活中充满数学，生活会变得更有意思。

本节并不是完整的高数计算手册，仅介绍了导数计算和偏导数计算的R语言实现。

导数计算
初等函数的导数公式
二阶导数计算
偏导数计算

1. 导数计算

导数(Derivative)是微分学的基本概念，用于计算函数的极值。导数的定义为，当函数y=f(x)在x0的某个领域内有定义，当自变量x在x0处取得增加Δx(点x0+Δx仍在该邻域内)时，相应的函数取得增量Δy=f(x0+Δx)-f(x0)；如果Δy与Δx之比当Δx趋于0时的极限存在，则称函数y=f(x)在点x0处可导，并称这个极限为函数y=f(x)在点x0处的导数，记为f`(x0)，即

也记作 y’|x=x0 ，dy/dx|x=x0 或 df(x)/dx|x=x0。

通过R语言可以使用deriv()函数直接进行导数的计算，比如要计算 y=x^3 的导数，根据导数计算公式，用于手动计算的变形结果为 y’=3x^2，当x=1时，y’=3,当x=2时，y’=12。

本节的系统环境

Win7 64bit
R: 3.1.1 x86_64-w64-mingw32/x64 (64-bit)

用R语言程序实现，代码如下。


> dx <- deriv(y ~ x^3, "x") ; dx  # 生成导数公式
expression({
    .value <- x^3
    .grad <- array(0, c(length(.value), 1L), list(NULL, c("x")))
    .grad[, "x"] <- 3 * x^2
    attr(.value, "gradient") <- .grad
    .value
})
> mode(dx)                        # 查看dx变量类型
[1] "expression"
> x<-1:2                          # 给自变量x赋值
> eval(dx)                        # 运行求导计算
[1] 1 8                           # 原函数的计算结果
attr(,"gradient")                 # 使用梯度下降法，导函数的计算结果
      x
[1,]  3                           # x=1,dx=3*1^2=3
[2,] 12                           # x=2,dx=3*2^2=12

用R语言程序计算的结果，与我们手动计算的结果是一致的。但计算过程其实是有很大区别的，我们手动计算时是通过给定的导数计算公式，变成后完成的计算。而用计算机程序计算时，是使用梯度下降法来计算一阶导数，是一种最优化的近似算法。对于手动计算导数时，如果函数比较复杂而且比较难应用可变形的公式，那么手动计算就会有非常大的困难，而计算机程序的方法是一般地导数计算方法，不会受到公式难于变形的影响。

我们使用deriv(expr, name)函数时通常要传2个参数，第一参数expr就是原函数公式，用~号来分隔公式的两边，第二参数name用于指定函数的自变量。deriv()函数会返回一个表达式expression类型变量，再用eval()函数运行这个表达式得到就可得到计算结果，如上面的代码实现。

如果希望以函数的形式调用计算公式，那么你还需要传第三个参数func，并让func参数为TRUE，参考下面的代码实现。

计算正弦函数y=sin(x)的导数，根据导数计算公式，用于手动计算的变形结果为 y’=cos(x)，当x=pi时，y’=-1，当x=4*pi时，y’=1，其中pi=π表示圆周率。


> dx <- deriv(y ~ sin(x), "x", func= TRUE) ; dx      # 生成导数公式的调用函数
function (x)
{
    .value <- sin(x)
    .grad <- array(0, c(length(.value), 1L), list(NULL, c("x")))
    .grad[, "x"] <- cos(x)
    attr(.value, "gradient") <- .grad
    .value
}
> mode(dx)                               # 检查dx的类型
[1] "function"
> dx(c(pi,4*pi))                         # 以参数作为自变量，进行函数调用
[1]  1.224606e-16 -4.898425e-16
attr(,"gradient")
      x                                  # 导函数的计算结果
[1,] -1                                  # x=pi,dx=cos(pi)=-1
[2,]  1                                  # x=4*pi,dx=cos(4*pi)=1

2. 初等函数的导数公式

对于基本的初等函数求导数，通过导数计算公式是可以直接手动完成计算的，下面为一元初等函数的导数计算公式。


函数          原函数            导函数
常数函数      y=C               y'=0
幂函数        y=x^n             y'=n*x^(n-1)
指数函数      y=a^x             y'=a^x*ln(a)
              y=exp(1)^x        y'=exp(1)^x
对数函数      y=log(x,base=a)   y'=1/(x*ln(a)) (a>0，且a!=1,x>0)
              y=ln(x)           y'=1/x
正弦函数      y=sin(x)          y'=cos(x)
余弦函数      y=cos(x)          y'=-sin(x)
正切函数      y=tan(x)          y'=sec(x)^2=1/cos(x)^2
余切函数      y=cot(x)          y'=-csc(x)^2=1/sin(x)^2
正割函数      y=sec(x)          y'=sec(x)*tan(x)
余割函数      y=csc(x)          y'=-csc(x)*cot(x)
反正弦函数    y=arcsin(x)       y'=1/sqrt(1-x^2)
反余弦函数    y=arccos(x)       y'=-1/sqrt(1-x^2)
反正切函数    y=arctan(x)       y'=1/(1+x^2)
反余切函数    y=arccot(x)       y'=-1/(1+x^2)
反正割函数    y=arcsec(x)       y'=1/abs(x)*(x^2-1)
反余割函数    y=arccsc(x)       y'=-1/abs(x)*(x^2-1)

公式的注释：

y是原函数，x是y函数的自变量，y’是y函数的导函数。
C,n,a为常数。
ln表示以自然常数e为底的对数
exp(1)表示自然常数e
log(x,base=a)表示，以常数a为底的对数
sqrt表示开平方
abs表示绝对值
正割函数sec，计算方法为 sec=1/cos(x)
余割函数csc，计算方法为 csc=1/sin(x)
余切函数cot，计算方法为 cot=1/tan(x)

注：以上公式不完全匹配于R语言函数

接下来，我们分别对这些一元初等函数进行一阶导数的计算。设y为原函数，x是y函数的自变量，且只有一个自变量。

常数函数

计算 y=3+10*x 函数的导数，根据导数计算公式，用于手动计算的变形结果为y’=0+10*x ，常数项3的导数为0，当x=1时，y’=10。


> dx<-deriv(y~ 3+10*x,"x",func = TRUE)  # 以函数形式生成导数公式
> dx(1)                                 # 传入自变量，并计算
[1] 13                                  # 原函数计算结果y=3+10*1=13
attr(,"gradient")
      x
[1,] 10         # 导函数计算结果y'=10*1=10

幂函数

计算 y=x^4 函数的导数，根据导数计算公式，用于手动计算的变形结果为y’=4*x^3，当x=2时，y’=32。


> dx<-deriv(y~x^4,"x",func = TRUE)
> dx(2)
[1] 16
attr(,"gradient")
      x
[1,] 32         # 导函数计算结果y'=4*x^3=4*2^3=32

指数函数

计算 y=4^x 函数的导数，根据导数计算公式，用于手动计算的变形结果为y’=4^x*ln(4)，当x=2时，y’=22.18071。


> dx<-deriv(y~4^x ,"x",func = TRUE)
> dx(2)
[1] 16
attr(,"gradient")
            x
[1,] 22.18071   # 导函数计算结果y'=4^x*log(4)=4*2^3=22.18071

计算 y=exp(1)^x 函数的导数，根据导数计算公式，用于手动计算的变形结果为y’=exp(1)^x，当x=2时，y’=y=7.389056。


> dx<-deriv(y~exp(1)^x ,"x",func = TRUE)
> dx(2)
[1] 7.389056
attr(,"gradient")
            x
[1,] 7.389056   # 导函数计算结果y'=exp(1)^x=exp(1)^2=7.389056

对数函数

计算 y=ln(x) 函数的导数，根据导数计算公式，用于手动计算的变形结果为y’=1/x，当x=2时，y’=0.5。


> dx<-deriv(y~log(x),"x",func = TRUE)
> dx(2)
[1] 0.6931472
attr(,"gradient")
       x
[1,] 0.5   # 导函数计算结果y'=1/x=1/2=0.5

计算 y=log2(x) 函数的导数，根据导数计算公式，用于手动计算的变形结果为y’=1/(x*log(2))，当x=3时，y’=0.4808983。

但用R语言编程时，只能计算以自然常数为底的对数的导数，对于原函数不是以自然常数为底的对数，首先要变换成以自然常数为底的对数再进行导数计算，根据对数的换底公式，把以2为底的对数转换为以自然常数为底的对数 y=log2(x)=log(x)/log(2)，


> dx<-deriv(y~log(x)/log(2),"x",func = TRUE)
> dx(3)
[1] 1.584963
attr(,"gradient")
             x
[1,] 0.4808983         # 导函数计算结果y'=1/(x*log(2)=1/(3*log(2)=0.4808983

正弦函数

计算 y=sin(x) 函数的导数，根据导数计算公式，用于手动计算的变形结果为y’=cos(x)，当x=pi时，y’=-1，其中pi=π表示圆周率。


> dx<-deriv(y~sin(x),"x",func = TRUE)
> dx(pi)
[1] 1.224606e-16
attr(,"gradient")
      x
[1,] -1   # 导函数计算结果y'=cos(x)=cos(pi)=-1

余弦函数

计算 y=cos(x) 函数的导数，根据导数计算公式，用于手动计算的变形结果为y’=-sin(x)，当x=pi/2时，y’=-1。


> dx<-deriv(y~cos(x),"x",func = TRUE)
> dx(pi/2)
[1] 6.123032e-17
attr(,"gradient")
      x
[1,] -1  # 导函数计算结果y'=-sin(x)=-sin(pi/2)=-1

正切函数

计算 y=tan(x) 函数的导数，根据导数计算公式，用于手动计算的变形结果为 y’=sec(x)^2=1/cos(x)^2，当x=pi/6时，y’=1.333333。


> dx<-deriv(y~tan(x),"x",func = TRUE)
> dx(pi/6)
[1] 0.5773503
attr(,"gradient")
            x
[1,] 1.333333  # 导函数计算结果y'=1/cos(x)^2=1/cos(pi/6)^2=1.333333

余切函数

计算 y=cot(x) 函数的导数，由于R语言没有cot()函数，所以根据三角公式我们动手变形原函数为y=cot(x)=1/tan(x)后再进行导数计算，根据导数计算公式，用于手动计算的变形结果为y’=-csc(x)^2=-1/sin(x)^2，当x=pi/6时，y’=-4。


> dx<-deriv(y~1/tan(x),"x",func = TRUE)
> dx(pi/6)
[1] 1.732051
attr(,"gradient")
      x
[1,] -4  # 导函数计算结果y'=-1/sin(x)^2=-1/sin(pi/6)^2=-4

反正弦函数

计算 y=asin(x) 函数的导数，根据导数计算公式，用于手动计算的变形结果为y’=1/sqrt(1-x^2)，当x=pi/6时，y’=1.173757。


> dx<-deriv(y~asin(x),"x",func = TRUE)
> dx(pi/6)
[1] 0.5510696
attr(,"gradient")
            x
[1,] 1.173757  # 导函数计算结果y'=1/sqrt(1-x^2)=1/sqrt(1-(pi/6)^2)=1.173757

反余弦函数

计算 y=acos(x) 函数的导数，根据导数计算公式，用于手动计算的变形结果为y’=-1/sqrt(1-x^2)，当x=pi/8时，y’=-1.08735。


> dx<-deriv(y~acos(x),"x",func = TRUE)
> dx(pi/8)
[1] 1.167232
attr(,"gradient")
            x
[1,] -1.08735    # 导函数计算结果y'=-1/sqrt(1-x^2)=-1/sqrt(1-(pi/8)^2)=-1.08735

反正切函数

计算 y=atan(x) 函数的导数，根据导数计算公式，用于手动计算的变形结果为y’=1/(1+x^2)，当x=pi/6时，y’=0.7848335。


> dx<-deriv(y~atan(x),"x",func = TRUE)
> dx(pi/6)
[1] 0.4823479
attr(,"gradient")
             x
[1,] 0.7848335   # 导函数计算结果y'= 1/(1+x^2) = 1/(1+(pi/6)^2)=0.7848335

3. 二阶导数计算

当我们对一个函数进行多次接连的求导计算，会形成高阶导数。
一般的，函数y=f(x)的导数y’=f'(x)仍然是x的函数，我们就把y’=f'(x)的导数叫做函数y=f(x)的二阶导数，记作y”，即

一阶导数的导数叫做二阶导数，二阶导数的导数叫做三阶导数，N-1阶导数的导数叫做N阶导数，习惯上把二阶以上的导数称之为高阶导数，

比如，计算 y=sin(a*x) 函数的二阶导数导数y”，其中a为常数，根据导数计算公式，用于手动计算的变形结果为一阶导数为y’=a*cos(a*x)，对y’再求导公式变形为，y”=-a^2*sin(a*x)

用R语言进行程序实现


> a<-2                 # 设置a的值
> dx<-deriv(y~sin(a*x),"x",func = TRUE) # 生成一阶导数公式
> dx(pi/3)                              # 计算一阶导数
[1] 0.8660254
attr(,"gradient")
      x
[1,] -1     # 导函数计算结果y'= a*cos(a*x)=2*cos(2*pi/3)=-1

> dx<-deriv(y~a*cos(a*x),"x",func = TRUE)    # 对一阶导函数求导
> dx(pi/3)
[1] -1
attr(,"gradient")
             x
[1,] -3.464102     # 导函数计算结果y'= -a^2*sin(a*x)=-2^2*sin(2*pi/3)=-3.464102

上面二阶导数的计算，我们是动手划分为两次求导进行计算的，利用deriv3()函数其实合并成一步计算。


> dx<-deriv3(y~sin(a*x),"x",func = TRUE)  # 生成二阶导数公式
> dx(pi/3)                                # 计算导数
[1] 0.8660254
attr(,"gradient")
      x
[1,] -1         # 一阶导数结果
attr(,"hessian")
, , x
             x
[1,] -3.464102  # 二阶导数结果

我们再计算另外一个二阶导数，计算y=a*x^4+b*x^3+x^2+x+c，其中a,b,c为常数a=2,b=1,c=3，
根据导数计算公式，用于手动计算的变形结果为一阶导数为y’=2*x^4+x^3+x^2+x+3=4*2*x^3+3*x^2+2*x+1,当x=2时，y’=81，
对y’再求导公式变形为，y”=3*4*2*x^2+2*3*x+2，当x=2时，y”=110。


> dx<-deriv3(y~a*x^4+b*x^3+x^2+x+c,"x",func=function(x,a=2,b=1,c=3){})  # 通过func参数，指定常数值
> dx(2)
[1] 49
attr(,"gradient")
      x
[1,] 81           # 一阶导数结果
attr(,"hessian")
, , x
       x
[1,] 110          # 二阶导数结果

这样就直接完成了二阶导数的计算，在R语言中二阶导数是可以直接求出的，想计算更高阶的导数就需要其他的数学工具包了。

4. 偏导数计算

在一元函数中，我们已经知道导数就是函数的变化率。对于二元函数我们同样要研究它的“变化率”。然而，由于自变量多了一个，情况就要复杂的多。在数学中，一个多变量的函数的偏导数，就是它关于其中一个变量的导数而保持其他变量恒定（相对于全导数，在其中所有变量都允许变化）。
偏导数的算子符号为:∂。记作∂f/∂x 或者 f’x。偏导数反映的是函数沿坐标轴正方向的变化率，在向量分析和微分几何中是很有用的。

在xOy平面内，当动点由P(x0,y0)沿不同方向变化时，函数f(x,y)的变化快慢一般说来是不同的，因此就需要研究f(x,y)在(x0,y0)点处沿不同方向的变化率。在这里我们只学习函数f(x,y)在x0y平面沿着平行于x0y轴和平行于y轴两个特殊方位变动时，f(x,y)的变化率。

x方向的偏导：
设有二元函数z=f(x,y)，点(x0,y0)是其定义域D内一点.把y固定在y0而让x在x0有增量△x，相应地函数z=f(x,y)有增量(称为对x的偏增量)△z=f(x0+△x,y0)-f(x0,y0)。如果△z与△x之比当△x→0时的极限存在，那么此极限值称为函数z=f(x,y)在(x0,y0)处对x的偏导数(partial derivative)。记作f’x(x0,y0)。

y方向的偏导：
函数z=f(x,y)在(x0,y0)处对x的偏导数，实际上就是把y固定在y0看成常数后，一元函数z=f(x,y0)在x0处的导数。同样，把x固定在x0,让y有增量△y,如果极限存在那么此极限称为函数z=(x,y)在(x0,y0)处对y的偏导数。记作f’y(x0,y0)

同样地，我们可以通过R语言的 deriv()函数进行偏导数的计算。下面我们计算一个二元函数f(x,y)=2*x^2+y+3*x*y^2的偏导数，由于二元函数曲面上每一点都有无穷多条切线，描述这个函数的导数就会相当困难。如果让其中的一个变量y取值为常数，那么就可以求出关于另一个自变量x的偏导数了，即∂f/∂x。

下面我们分别对x,y两个自变量求偏导数，设变量y为常数，计算x的偏导数∂f/∂x=4*x+3*y^2，当x=1,y=1时，x的偏导数∂f/∂x=4*x+3*y^2=7。设变量x为常数，计算y的偏导数∂f/∂y=1+6*x*y，当x=1,y=1时，y的偏导数∂f/∂x=1+6*x*y=7。

用R语言程序实现。


> fxy = expression(2*x^2+y+3*x*y^2)     # 二元函数公式
> dxy = deriv(fxy, c("x", "y"), func = TRUE)
> dxy
function (x, y)
{
    .expr4 <- 3 * x
    .expr5 <- y^2
    .value <- 2 * x^2 + y + .expr4 * .expr5
    .grad <- array(0, c(length(.value), 2L), list(NULL, c("x","y")))
    .grad[, "x"] <- 2 * (2 * x) + 3 * .expr5
    .grad[, "y"] <- 1 + .expr4 * (2 * y)
    attr(.value, "gradient") <- .grad
    .value
}
> dxy(1,1)                          # 设置自变量
[1] 6
attr(,"gradient")
     x y                            # 计算结果，x的偏导数为7，y的偏导数为7
[1,] 7 7

偏导数的程序计算结果与手动计算结果是一致的。下面我们再求一个复杂函数偏导数，计算一个二元函数f(x,y)=x^y + exp(x * y) + x^2 – 2 * x * y + y^3 + sin(x*y)在点(1,3)和点(0,0)的偏导数。

R语言程序实现。


> fxy = expression(x^y + exp(x * y) + x^2 - 2 * x * y + y^3 + sin(x*y))
> dxy = deriv(fxy, c("x", "y"), func = TRUE)
> dxy(1,3)        # 设置自变量
[1] 43.22666
attr(,"gradient")
            x        y
[1,] 56.28663 44.09554        # 计算结果，x的偏导数为56.28663，y的偏导数为 44.09554
> dxy(0,0)
[1] 2
attr(,"gradient")
       x    y
[1,] NaN -Inf                 # 计算结果，x的偏导数无意义，y的偏导数负无穷大

对于计算的结果，有异议的同学，可以尝试动手计算。

本文我们掌握了R语言对于高等数学的导数计算方法，真的是非常方便，这下更有动力学习高数了。

转载请注明出处：
http://blog.fens.me/r-math-derivative/

打赏作者

排行榜

Blog Archives

Posted:

Tags:

Comments:

R语言的导数计算

1. 导数计算

2. 初等函数的导数公式

3. 二阶导数计算

4. 偏导数计算

站内导航

最新文章

最新评论

最热文章