R的极客理想系列文章,涵盖了R的思想,使用,工具,创新等的一系列要点,以我个人的学习和体验去诠释R的强大。
R语言作为统计学一门语言,一直在小众领域闪耀着光芒。直到大数据的爆发,R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入,R语言的社区在迅速扩大成长。现在已不仅仅是统计领域,教育,银行,电商,互联网….都在使用R语言。
要成为有理想的极客,我们不能停留在语法上,要掌握牢固的数学,概率,统计知识,同时还要有创新精神,把R语言发挥到各个领域。让我们一起动起来吧,开始R的极客理想。
关于作者:
- 张丹,分析师/程序员/Quant: R,Java,Nodejs
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-kdtree/
前言
多维向量数据检索,在自然语言处理以及标签向量匹配等应用场景,越来越多的被使用到。提升匹配效率,就能使用体验有巨大的改善。本文从kd树的底层数据结构,和R语言算法实现的角度,介绍kdtree在多维度数据匹配过程中的应用。
目录
- KD Tree算法介绍
- 用R语言实现KD Tree
- 进行三维索引匹配
1. KD Tree算法介绍
k-D Tree(KDT , k-Dimension Tree) 是一种可以对K 维资料进行划分的资料结构,可以看成二元搜索树的一种延伸,不断的对空间中的维度做划分,利用搜索树剪枝的特性缩短时间复杂度,主要应用在多维空间搜寻,例如最近邻居搜索。在结点数 n 远大于 2^k 时,应用 k-D Tree 的时间效率很好。
k-D Tree 具有二叉搜索树的形态,二叉搜索树上的每个结点都对应 k 维空间内的一个点。其每个子树中的点都在一个 k 维的超长方体内,这个超长方体内的所有点也都在这个子树中。
假设我们已经知道了 k 维空间内的 n 个不同的点的坐标,要将其构建成一棵 k-D Tree,步骤如下:
- 若当前超长方体中只有一个点,返回这个点。
- 选择一个维度,将当前超长方体按照这个维度分成两个超长方体。
- 选择切割点:在选择的维度上选择一个点,这一维度上的值小于这个点的归入一个超长方体(左子树),其余的归入另一个超长方体(右子树)。
- 将选择的点作为这棵子树的根节点,递归对分出的两个超长方体构建左右子树,维护子树的信息。
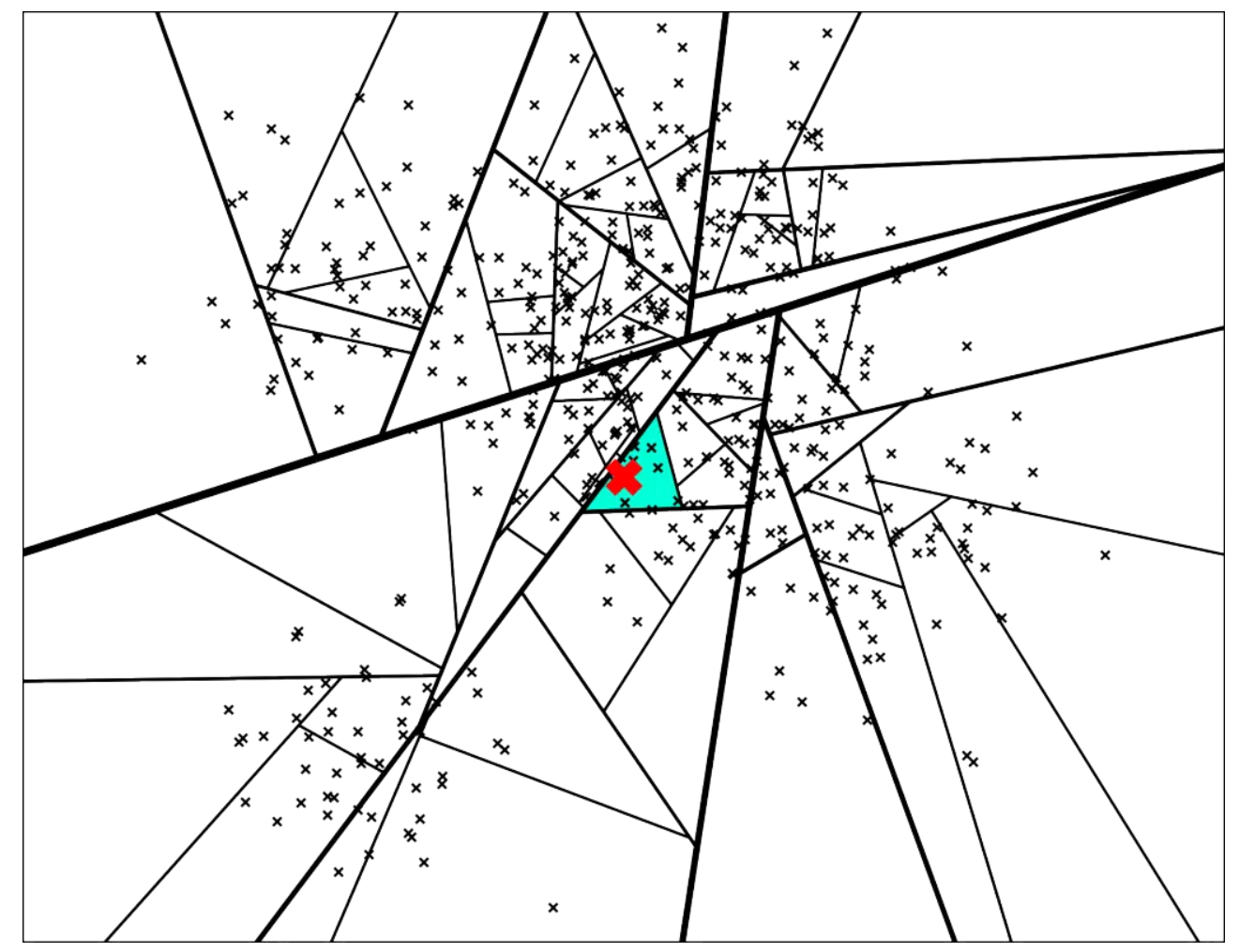
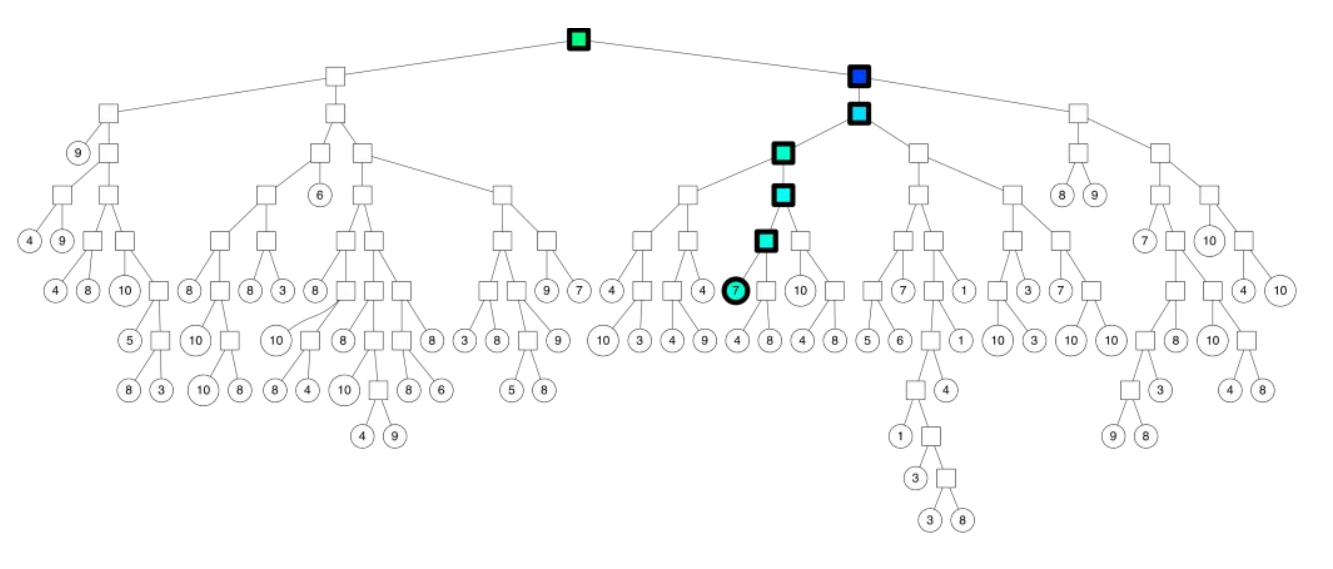
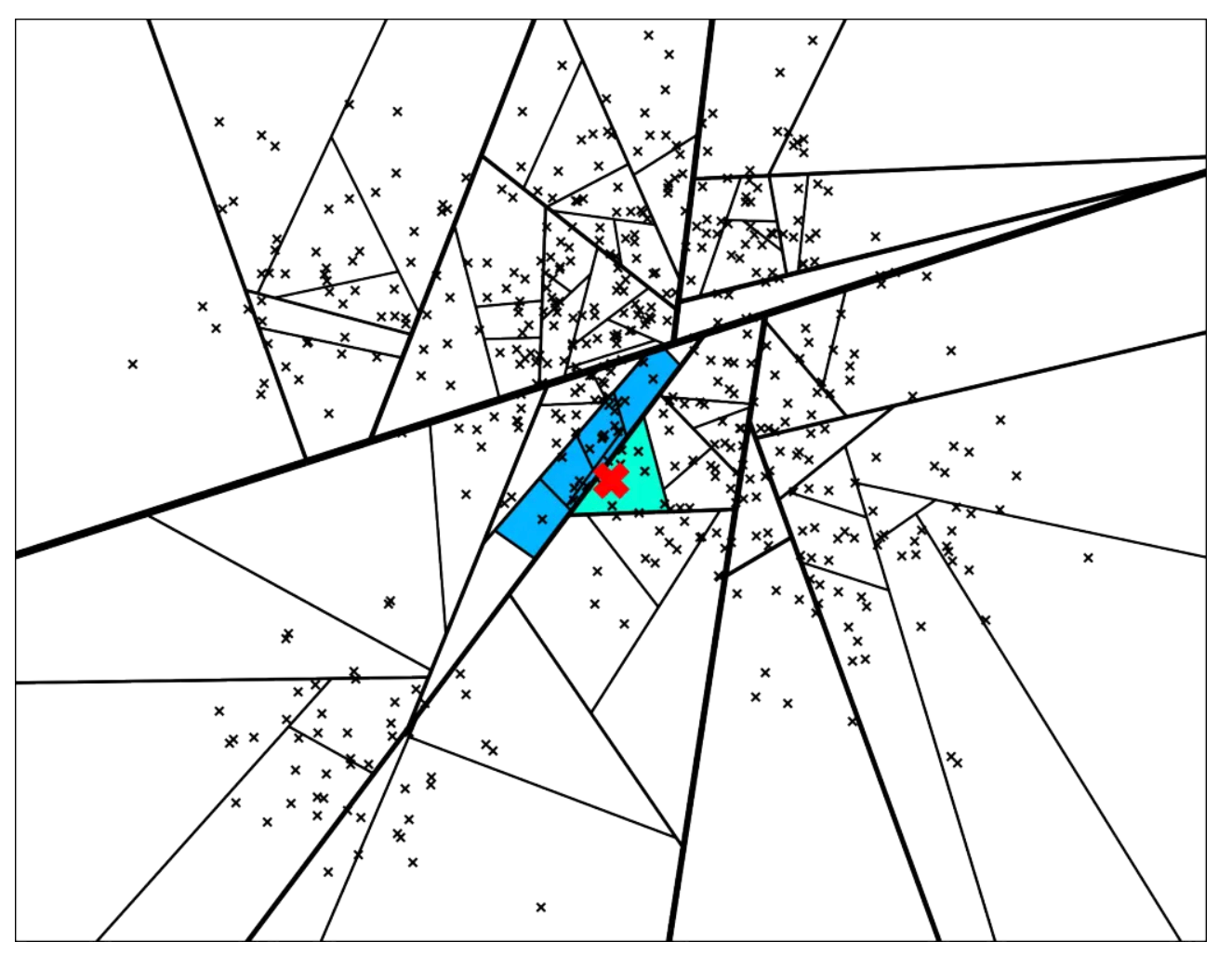
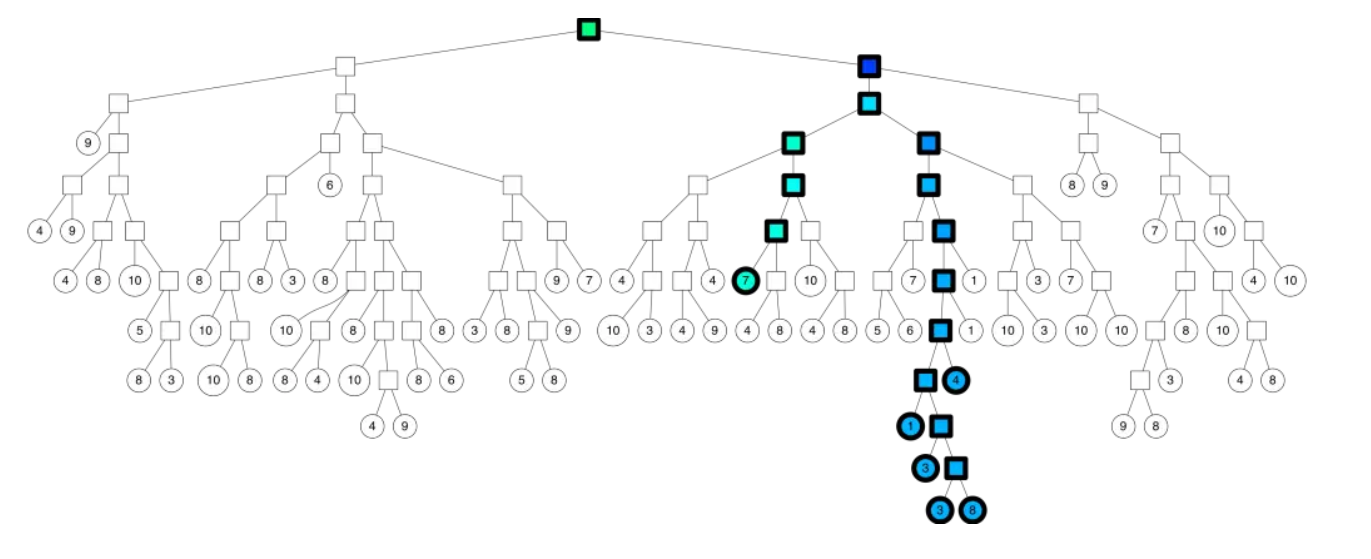
以k=2时举例
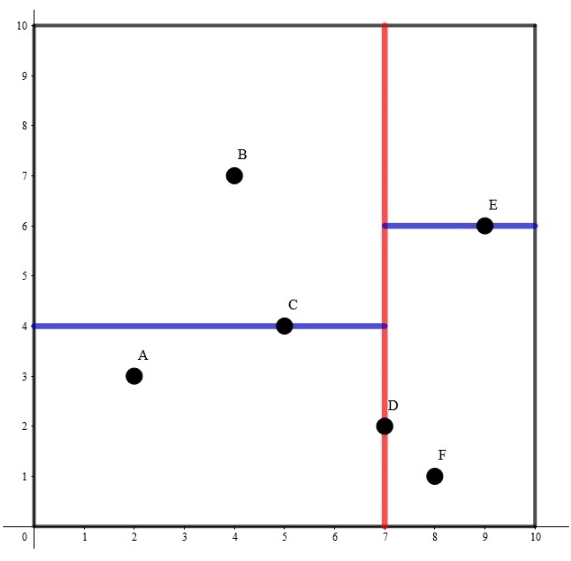
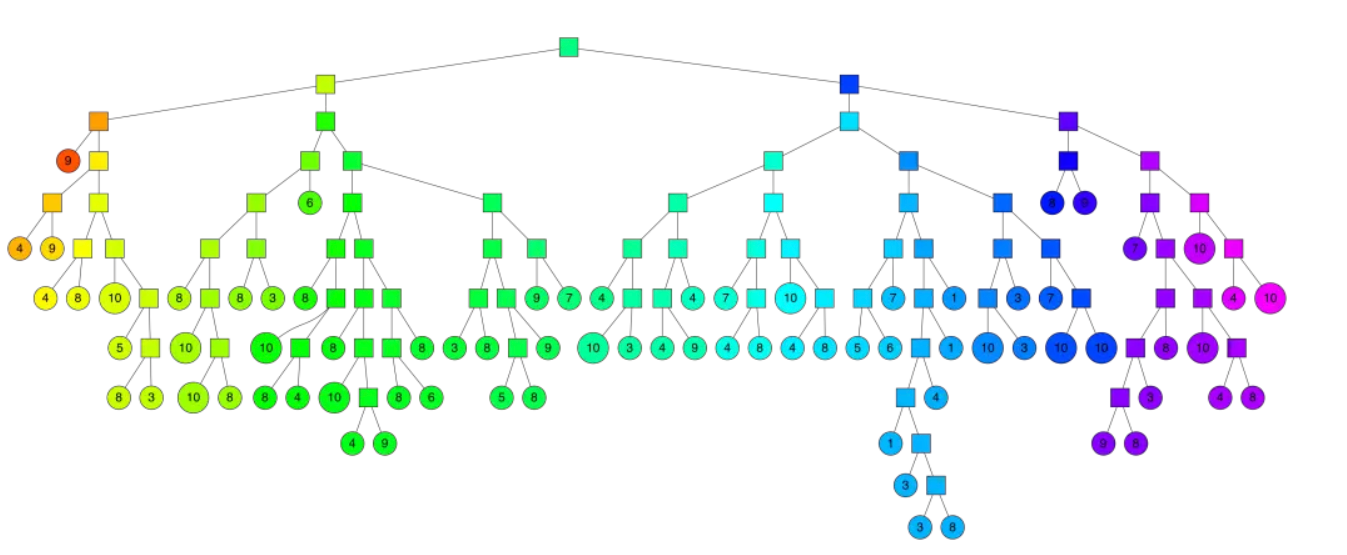
其构建出 k-D Tree 的形态可能是这样的:
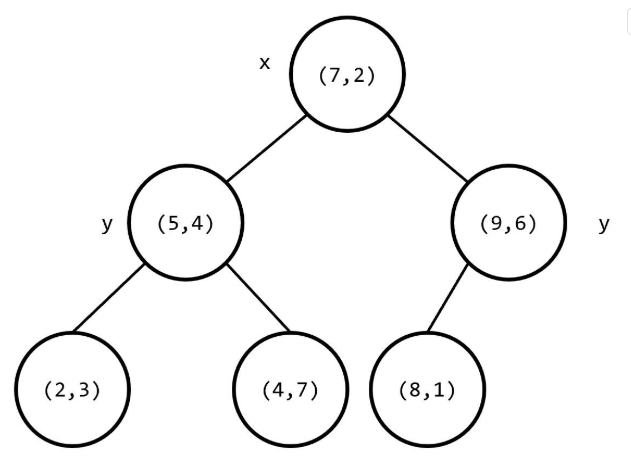
其中树上每个结点上的坐标是选择的分割点的坐标,非叶子结点旁的 x 或 y 是选择的切割维度。
这样的复杂度无法保证。对于 2,3 两步,我们提出两个优化:
- 轮流选择 k 个维度,以保证在任意连续 k 层里每个维度都被切割到。
- 每次在维度上选择切割点时选择该维度上的 中位数,这样可以保证每次分成的左右子树大小尽量相等。
可以发现,使用优化 2 后,构建出的 k-D Tree 的树高最多为 log(n)+O(1)。
现在,构建 k-D Tree 时间复杂度的瓶颈在于快速选出一个维度上的中位数,并将在该维度上的值小于该中位数的置于中位数的左边,其余置于右边。如果每次都使用 sort 函数对该维度进行排序,时间复杂度是 O(nlog^2(n)) 的。事实上,单次找出 n 个元素中的中位数并将中位数置于排序后正确的位置的复杂度可以达到 O(n)。
我们来回顾一下快速排序的思想。每次我们选出一个数,将小于该数的置于该数的左边,大于该数的置于该数的右边,保证该数在排好序后正确的位置上,然后递归排序左侧和右侧的值。这样的期望复杂度是 O(nlog(n)) 的。但是由于 k-D Tree 只要求要中位数在排序后正确的位置上,所以我们只需要递归排序包含中位数的 一侧。可以证明,这样的期望复杂度是 O(n) 的。借助这种思想,构建 k-D Tree 时间复杂度是 O(nlog(n)) 的。
参考文章:https://oi-wiki.org/ds/kdt/
2. 用R语言实现KD Tree
首先,安装less(Learning with Subset Stacking)包,less包中包含了多种的算法,DKTree就是集成的一种算法。
# 安装
> install.packages("less")
# 加载
> library(less)
选定数据集
# 选定数据集,以iris数据集为例,取前2例
> dat<-iris[,1:2]
# 查看数据内容
> head(dat)
Sepal.Length Sepal.Width
1 5.1 3.5
2 4.9 3.0
3 4.7 3.2
4 4.6 3.1
5 5.0 3.6
6 5.4 3.9
创建一个kdtree实例化对象kdt,kdt对象中一共3个函数,分别是clone,initialize,query。
# 创建
> kdt <- KDTree$new(dat)
# 查看数据结构
> kdt
Public:
clone: function (deep = FALSE)
initialize: function (X = NULL)
query: function (query_X = private$X, k = 1)
Private:
X: data.frame
接下来,我们生成一些与创建 kdtree 不同的查询点,用于查询。
> q_data <- iris[1:5,1:2] + array(rnorm(10)*0.1, dim=c(5,2))
> q_data
Sepal.Length Sepal.Width
1 5.067010 3.464073
2 4.913018 3.100844
3 4.678508 3.203468
4 4.634521 3.105371
5 4.948339 3.594034
把q_data输入kdt对象,用于kdtree查询。
# 查询k=2,为二维
> res<-kdt$query(query_X = q_data, k = 2)
> res
$nn.idx # 输出索引号
[,1] [,2]
[1,] 18 1
[2,] 10 35
[3,] 30 3
[4,] 4 48
[5,] 38 5
$nn.dists # 输出距离
[,1] [,2]
[1,] 0.04877580 0.04877580
[2,] 0.01304518 0.01304518
[3,] 0.02177005 0.02177005
[4,] 0.03493634 0.10072915
[5,] 0.04870594 0.05200411
通过索引号,还原的dat的原始数据中
> src<-matrix(col1=dat[res$nn.idx[,1],1],col2=dat[res$nn.idx[,2],2])
> src
col1 col2
1 5.1 3.5
2 4.9 3.1
3 4.7 3.2
4 4.6 3.2
5 4.9 3.6
3. 进行三维索引匹配
接下来,我们再尝试一下三维索引的匹配。
> # 三维数据集
> dat<-iris[,1:3]
> head(dat)
Sepal.Length Sepal.Width Petal.Length
1 5.1 3.5 1.4
2 4.9 3.0 1.4
3 4.7 3.2 1.3
4 4.6 3.1 1.5
5 5.0 3.6 1.4
6 5.4 3.9 1.7
# 建树
> kdt <- KDTree$new(dat)
# 生成三维测试数据
> q_data <- iris[1:5,1:3] + array(rnorm(10)*0.3, dim=c(5,2))
> q_data
Sepal.Length Sepal.Width Petal.Length
1 5.193700 3.404217 1.493700
2 5.078012 3.019615 1.578012
3 4.914997 3.498524 1.514997
4 4.593170 2.982210 1.493170
5 5.094704 3.149830 1.494704
# 获得匹配结果
> res<-kdt$query(query_X = q_data, k = 3)
> res
$nn.idx
[,1] [,2] [,3]
[1,] 40 29 28
[2,] 26 35 10
[3,] 44 8 38
[4,] 4 46 13
[5,] 10 35 50
$nn.dists
[,1] [,2] [,3]
[1,] 0.09400598 0.09400598 0.09619658
[2,] 0.08339090 0.21032310 0.21032310
[3,] 0.12022173 0.13098663 0.15409891
[4,] 0.11818578 0.22754310 0.22754310
[5,] 0.20104879 0.20104879 0.20121780
通过KDTree的,能快速的让我们从多维数据中,找到最紧邻的点,进行数据搜索。
本文的代码已上传到github:https://github.com/bsspirit/r-string-match/blob/main/kdtree.r
转载请注明出处:
http://blog.fens.me/r-kdtree/