Blog Archives

Prolog语言知识推理系列文章，不同编程语言有着不同编程视角，JAVA是面向对象，Nodejs是异步回调，R语言是统计算法，Prolog就是知识推理。每种语言都是独特的，如果想把一门语言学好用好，关键是利用语言的特点，做对的事情。

本系列文章主要介绍Prolog语言，从入门安装到知识推理。Prolog是完全不一样的，他没有复杂的程序结构，也不是为了解决算法问题，而是专注于逻辑推理，擅长解决抽象的问题。

关于作者：

• 张丹，分析师/程序员/Quant: R,Java,Nodejs
• blog: http://fens.me
• email: bsspirit@gmail.com

转载请注明出处：
http://blog.fens.me/prolog-recursion/

前言

Prolog有简单的语法结构，用来进行事实描述非常容易，在实际编程时，除了有明确的事实定义，还有很多逻辑推理的算法需要来解决，比如递归的程序涉设计。

用prolog的语法，在思考逻辑和程序写法上，与其他高级编程语言有非常大的跨度，需要我们切换大脑思路。我就在尝试中，消耗大量脑细胞，也还是没有完全掌握。

目录

1. 什么是递归？
2. 两个数比大小
3. 循环语句实现
4. factorial阶乘计算
5. hanoi游戏推理

1. 什么是递归？

什么是递归？递归是指一种通过重复，将问题分解为同类的子问题，而解决问题的方法。函数直接或间接调用自身的过程称为递归，而相应的函数称为递归函数。使用递归算法，可以很容易地解决某些问题。此类问题的示例包括：汉诺塔（hanoi），树的遍历，图的图的深度优先搜索等。

Prolog的递归实现很奇怪，真的是每种编程语言都有自己的特点，要理解语言的特性并不容易，那么下面就以递归来做举例，让大家也来了解一下，如何用prolog实现递归的逻辑推理过程。

2. 两个数比大小

在recursion.pl文件中，定义bigger()规则，用于比较进行两数比较大操作，返回更大的数字。按照prolog的编程逻辑，我们给bigger规则定义三个参数bigger(A, B, C)。

• 参数1，用于接收第1个数字。
• 参数2，用于接收第2个数字。
• 参数3，用于返回最大的数字。

% 两个数比大小
bigger(X, Y, X) :- X >= Y,!.
bigger(X, Y, Y) .

我们还需要定义，比较大小的规则，设定2条规则。

• 第1行，用于定义X >= Y时，返回X，最后的!表示不继续向下执行。
• 第2行，用于定义不满足第1行的条件时，返回Y。

脚本执行：

% X=3, Y=5，则返回X=5
3 ?- bigger(3,5,X).
X = 5.

% X=5, Y=3，则返回X=5
4 ?- bigger(5,3,X). 
X = 5.

好诡异！！我们跟踪一下prolog的程序逻辑，使用trace.命令，按c执行每一步，跳出正在执行的规则按s，完成整个规则计算按n。

% 启动跟踪日志
5 ?- trace.
true.

% 执行语句
[trace] 5 ?- bigger(3,5,X).
   Call: (10) bigger(3, 5, _8002) ? creep   % 进入 bigger(X, Y, X) 规则
   Call: (11) 3>5 ? creep                % 进行 X >= Y 判断
   Fail: (11) 3>5 ? creep                % 进行 X >= Y 判断失败
   Redo: (10) bigger(3, 5, _8002) ? creep   % 继续执行，进入 bigger(X, Y, Y)规则
   Exit: (10) bigger(3, 5, 5) ? creep       % 结束返回
X = 5.

从运行过程跟踪情况来看，2个规则会按顺序执行，第1个规则不满足，则执行第2个规则。

接下来，再执行一下第二语句，让第一个参数为5，第二个参数为3，bigger(5,3,X). 。

% 执行语句
[trace] 6 ?- bigger(5,3,X).                 % 进入 bigger(X, Y, X) 规则
   Call: (10) bigger(5, 3, _90) ? creep     % 进行 X >= Y 判断
   Call: (11) 5>3 ? creep                % 进行 X >= Y 判断成功
   Exit: (11) 5>3 ? creep
   Exit: (10) bigger(5, 3, 5) ? creep       % 结束返回
X = 5.

从运行过程跟踪情况来看，第1个规则满足条件，由于设置了!号，就不进行行第2个规则的执行了。

3. 循环语句实现

在recursion.pl文件中，继续定义loop()规则，用于实现一个循环操作，不需要返回值，实现输入一个数字，倒叙打印出从输入的数字到1的所有连续整数，只有1个参数用于接收输入的数字。

% 循环语句实现
loop(0).  
loop(N) :- 
    N>0, write(N), nl,
    S is N-1, loop(S).  

规则定义：

• 第1行，当参数为0时，程序结束。
• 第2行，当参数大于0时，输入当前参数，让参数减一，再递归调用loop()规则

脚本执行：

10 ?- loop(3).  
3
2
1
true .

我们使用trace.命令进行程序跟踪。

% 启动跟踪日志
11 ?- trace.
true.

% 执行语句
[trace] 12 ?- loop(3).              
   Call: (10) loop(3) ? creep        % 进入 loop(N) 规则   
   Call: (11) 3>0 ? creep         % 判断 N>0
   Exit: (11) 3>0 ? creep
   Call: (11) write(3) ? creep       % 输出N
3
   Exit: (11) write(3) ? creep
   Call: (11) nl ? creep

   Exit: (11) nl ? creep
   Call: (11) _7946 is 3+ -1 ? creep   % 执行S=N-1=3-1=2
   Exit: (11) 2 is 3+ -1 ? creep
   Call: (11) loop(2) ? creep          % 进行loop(2)规则
   Call: (12) 2>0 ? creep           
   Exit: (12) 2>0 ? creep
   Call: (12) write(2) ? creep         % 输出2
2
   Exit: (12) write(2) ? creep
   Call: (12) nl ? creep

   Exit: (12) nl ? creep
   Call: (12) _8348 is 2+ -1 ? creep   % 执行S=N-1=2-1=1
   Exit: (12) 1 is 2+ -1 ? creep
   Call: (12) loop(1) ? creep          % 进行loop(1)规则
   Call: (13) 1>0 ? creep
   Exit: (13) 1>0 ? creep
   Call: (13) write(1) ? creep
1                                      % 输出1
   Exit: (13) write(1) ? creep
   Call: (13) nl ? creep

   Exit: (13) nl ? creep
   Call: (13) _8750 is 1+ -1 ? creep    % 执行S=N-1=1-1=0
   Exit: (13) 0 is 1+ -1 ? creep        % 判断 N>0 失败
   Call: (13) loop(0) ? creep           % 进入 loop(0) 规则   
   Exit: (13) loop(0) ? creep           % 结束返回
   Exit: (12) loop(1) ? creep
   Exit: (11) loop(2) ? creep
   Exit: (10) loop(3) ? creep           
true .

这个循环的程序中，我们就用到了递归计算，

4. factorial阶乘计算

factorial阶乘计算这个例子，在我们学习每一种语言时，都会这个问题的求解，而且都是用递归来实现的，那么对于prolog编程来说，我们也来试怎么实现。

在recursion.pl文件中，继续定义factorial()规则，用于实现数字阶乘计算，需要返回值。实现输入一个数字，计算从1到这个数字阶乘结果，并返回。

我们需要定义2个参数，

• 参数1，用于接收数字。
• 参数2，用于返回阶乘的计算结果。

% factorial阶乘计算
factorial(0,1).   
factorial(N,F) :-    
    N>0,   
    N1 is N-1,   
    factorial(N1,F1),   
    F is N * F1.  

规则定义：

• 第1行，当第一个参数 输入数字为0时，直接返回1。
• 第2行，当第一个参数 N 输入数字大于0时，把输入数字减一，递归调用factorial()规则，获得递归的结果保存在第二个参数F中

脚本执行：

% 计算3的阶乘，返回值为X=6
19 ?- factorial(3,X).
X = 6 .

程序跟踪

[trace] 19 ?- factorial(3,X).
   Call: (10) factorial(3, _3310) ? creep     % 进入 factorial(3,F) 规则
   Call: (11) 3>0 ? creep
   Exit: (11) 3>0 ? creep
   Call: (11) _3834 is 3+ -1 ? creep
   Exit: (11) 2 is 3+ -1 ? creep
   Call: (11) factorial(2, _3924) ? creep     % 进入 factorial(2,F) 规则
   Call: (12) 2>0 ? creep
   Exit: (12) 2>0 ? creep
   Call: (12) _4060 is 2+ -1 ? creep
   Exit: (12) 1 is 2+ -1 ? creep
   Call: (12) factorial(1, _4150) ? creep     % 进入 factorial(1,F) 规则
   Call: (13) 1>0 ? creep
   Exit: (13) 1>0 ? creep
   Call: (13) _4286 is 1+ -1 ? creep
   Exit: (13) 0 is 1+ -1 ? creep
   Call: (13) factorial(0, _4376) ? creep    
   Exit: (13) factorial(0, 1) ? creep         % 进入 factorial(0,1) 规则
   Call: (13) _4468 is 1*1 ? creep            
   Exit: (13) 1 is 1*1 ? creep
   Exit: (12) factorial(1, 1) ? creep         % F返回1= 1*1
   Call: (12) _4606 is 2*1 ? creep            
   Exit: (12) 2 is 2*1 ? creep                % F返回2 = 2*1
   Exit: (11) factorial(2, 2) ? creep
   Call: (11) _3310 is 3*2 ? creep            
   Exit: (11) 6 is 3*2 ? creep                % F返回6= 3*2
   Exit: (10) factorial(3, 6) ? creep
X = 6 .                                       % F返回6

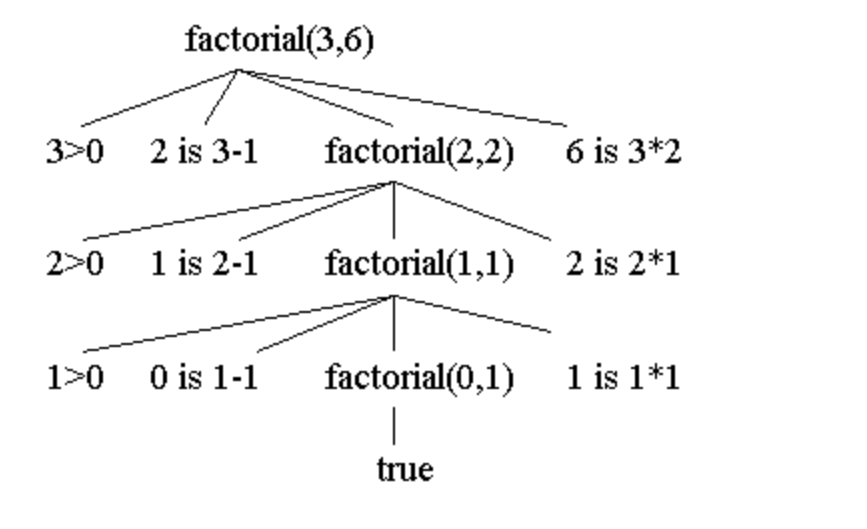
根据程序追踪的递归调用过程，我们也可以用一个图来表达程序在执行过程中的调用关系。

这个计算过程，我们需要用到递归的调用方法，同时需要存储递归返回的结果，用于累计每次计算的值。

5. hanoi游戏推理

汉诺塔（hanoi）一个是数学游戏，它由三根杆和许多不同大小的圆盘组成，可以滑到任何杆上。要求圆盘在一个杆上的排列顺序整齐，大小按升序排列，顶部最小，从而形成圆锥形。

我要解决如何让所有的圆盘，从一个杆按顺序移动到另一个杆，规则：

• 一次只能移动一个盘子。
• 每一次操作，取出一个杆子最上面的盘子，并将其放在另一个杆子的顶部或空杆上。
• 只能将小盘子放在大盘子上面

对于4个盘子的解密过程，可以参考下图。

在recursion.pl文件中，继续定义hanoi()规则，用于实现上面的解密过程，并输出操作步骤。我们定义3个规则。

• hanoi()，用于启动游戏
• move()，用于盘子的移动操作
• inform()，用于输出操作日志

% hanoi游戏推理
hanoi(N) :- 
    move(N, left,  right, centre).

move(0, _, _, _) :- !.
move(N, A, B, C) :-
    M is N-1,
    move(M, A, C, B), print(A, B), move(M, C, B, A).

print(X, Y) :-
    write("move disc from "), write(X), write(" to ") ,write(Y),
    nl.    

脚本执行：

32 ?- hanoi(4).     
move disc from left to centre
move disc from left to right
move disc from centre to right
move disc from left to centre
move disc from right to left
move disc from right to centre
move disc from left to centre
move disc from left to right
move disc from centre to right
move disc from centre to left
move disc from right to left
move disc from centre to right
move disc from left to centre
move disc from left to right
move disc from centre to right
true.

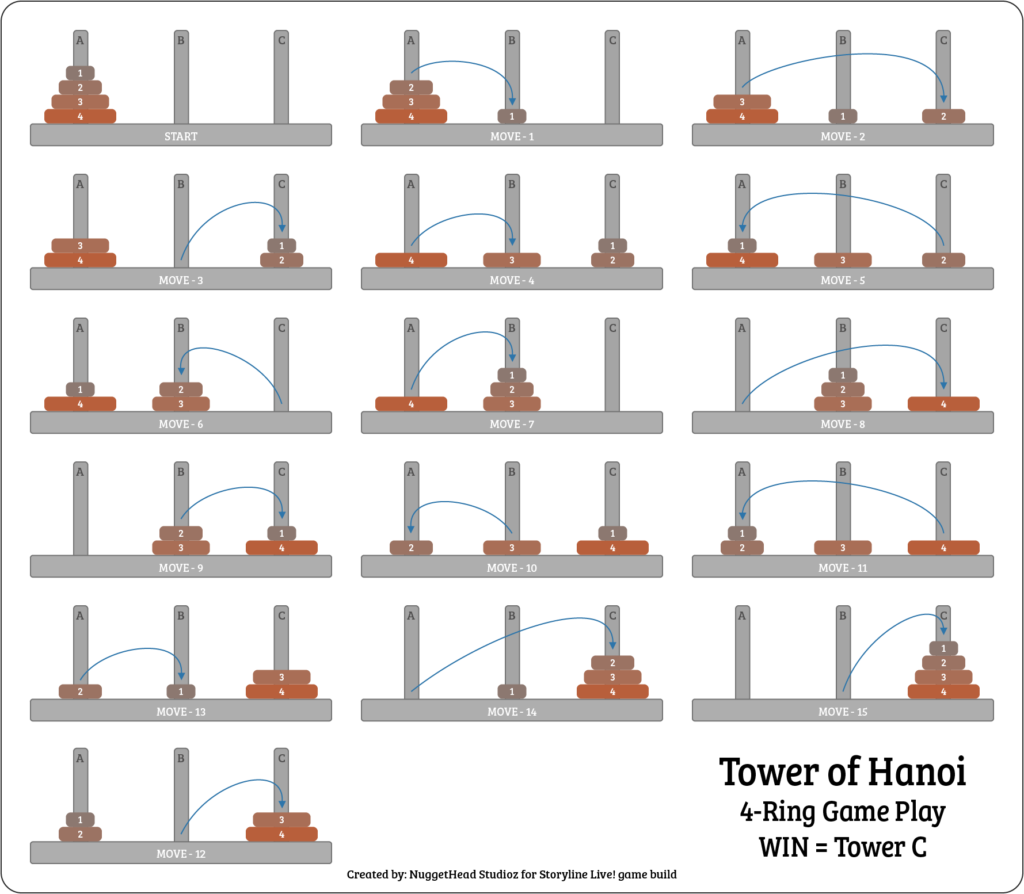
操作日志的过程，就与上面图中手动移动过程是一致的，大家可以用trace.自己跟踪一下程序的运行过程。通过4个小例子，让我快速熟悉一下prolog的编程思路，确实与其他语言都不一样的！有意思！

本文的完整代码，可以在github上找到：https://github.com/bsspirit/prolog-learning/tree/main/04 recursion

同样，本文还是对于prolog的初探，进行逻辑推理，从浅入入深的过程，希望本文能让所有的prolog新手快速上手。

转载请注明出处：
http://blog.fens.me/prolog-recursion/