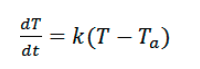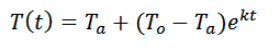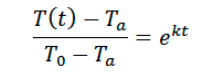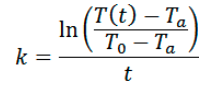R的极客理想系列文章,涵盖了R的思想,使用,工具,创新等的一系列要点,以我个人的学习和体验去诠释R的强大。
R语言作为统计学一门语言,一直在小众领域闪耀着光芒。直到大数据的爆发,R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入,R语言的社区在迅速扩大成长。现在已不仅仅是统计领域,教育,银行,电商,互联网….都在使用R语言。
要成为有理想的极客,我们不能停留在语法上,要掌握牢固的数学,概率,统计知识,同时还要有创新精神,把R语言发挥到各个领域。让我们一起动起来吧,开始R的极客理想。
关于作者:
- 张丹(Conan), 程序员/Quant: Java,R,Nodejs
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-newton-cooling
前言
牛顿冷却定律是经典的热力学模型,描述了温度与时间之间的指数衰减函数。我们通过对基础科学的研究,可以极大地开阔思路,并形成跨学科的解决方案,引用新的思考维度,解决现有场景的难题。站在物理学的制高点,推进数据科学的发展。
目录
- 牛顿冷却定律
- 数据集
- 程序实现
1. 牛顿冷却定律
牛顿冷却定律,是一个热力学的基本定律,指物体所损失的热的速率与物体和其周围环境间的温度差是成比例的。当物体表面与周围存在温度差时,单位时间从单位面积散失的热量与温度差成正比,比例系数称为热传递系数。牛顿冷却定律,是由英国物理学家艾萨克·牛顿爵士所提出的,是一个经验发现的规律。
当物体处于与周围环境不同的温度时,它将逐渐冷却或加热直至温度相等。我们每个人都在生活中遇到过,比如煮水沏茶的过程,把凉水烧热到100度的高温,然后沏茶,再等一会儿,到达可以喝的温度。水从100度的高温,自然到达可以喝的温度,就是冷却的过程,即物体温度与周围环境温度热交换的过程。
公式:
公式解释:
- T: 温度
- t: 时间
- T(t):t时刻的温度
- Ta:代表室温,T(t)-Ta就是当前温度与室温之间的温差。当前温度高于室温时,T(t)-Ta > 0。
- T0:初始温度
- k:传热系数,常数,表示室温与降温速率之间的比例关系
- dT/dt:温度和时间的微分形式,表示物体的温度随时间下降的速度
把上面微分方程进行数学变型,产生可以下面等式。
经过数学变型后,就容易进行计算了。由于k是一个常数,所以我们需要先计算出k值,再用k值计算出每一时刻的模型值,最后用模型值和测试值进行对比。
进行k值的公式变型:
2. 数据集
用数据说话,我们通过一个实验来验证牛顿冷去定律,把牛顿冷却定律计算的数值与真实数据的测量值进行拟合。实验数据来源:Newton’s Law of Cooling An Experimental Investigation
实验开始,准备3个烧杯加热至沸腾,让3个烧杯中的水自然冷却,记录60分钟每分钟3个烧杯中水的温度。3个烧杯水中水量不同,第一个烧杯放入100毫升水,第二个烧杯放入300毫升水,第三个烧杯放入800毫升水。每个烧杯都有自己的温度计,温度计在测量之间保持在烧杯中,确保不会出现温度滞后。每分钟测量每个烧杯中水的温度,环境温度为23°C。
开发环境所使用的系统环境
- Win10 64bit
- R: 3.6.1 x86_64-w64-mingw32/x64 b4bit
记录3个烧杯温度的数据集,共4列,保存文件为Temperature.csv。
- time_min:分钟,冷却时间,从0分钟到60分钟
- temp_100ml:温度(摄氏度),100ml水随时间变化的温度
- temp_300ml:温度(摄氏度),300ml水随时间变化的温度
- temp_800ml:温度(摄氏度),800ml水随时间变化的温度
> dat
time_min temp_100ml temp_300ml temp_800ml
1 0 100 100 100
2 1 95 95 96
3 2 82 91 95
4 3 79 87 92
5 4 74 84 90
6 5 70 81 88
7 6 67 78 85
8 7 65 76 83
9 8 61 73 80
10 9 59 71 78
11 10 57 70 76
12 11 56 68 75
13 12 54 66 74
14 13 52 64 73
15 14 51 63 71
16 15 50 61 70
17 16 49 60 68
18 17 48 58 66
19 18 47 58 66
20 19 45 56 65
21 20 45 55 63
22 21 44 55 62
23 22 43 54 61
24 23 42 53 60
25 24 42 52 60
26 25 41 51 59
27 26 41 50 58
28 27 40 49 56
29 28 39 48 56
30 29 38 48 55
31 30 38 47 54
32 31 38 46 53
33 32 38 46 52
34 33 37 45 52
35 34 36 45 51
36 35 36 45 50
37 40 34 42 47
38 45 33 40 45
39 50 31 38 43
40 55 30 37 41
41 60 29 36 40
观察数据集,用散点图画出的测试值的3种情况。
# 加载数据集
> dat<-read.csv("Temperature.csv")
# 以散点图观察数据
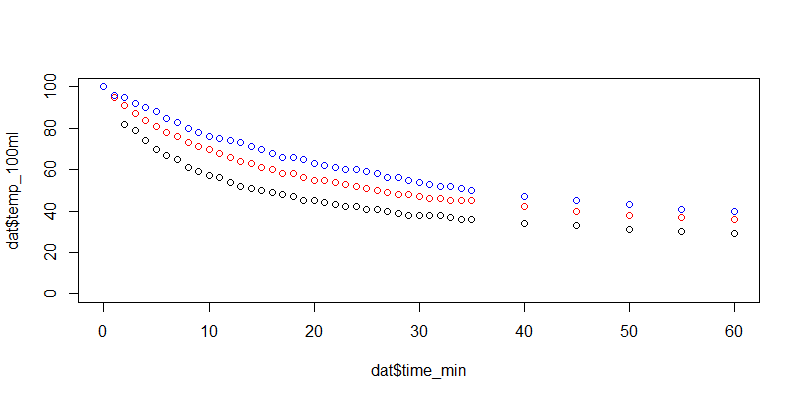
> plot(dat$time_min,dat$temp_100ml)
> points(dat$time_min,dat$temp_300ml,col="red")
> points(dat$time_min,dat$temp_800ml,col="blue")
- x轴为时间
- y轴为维度
- 黑色散点,100毫升水的温度变化
- 红色散点,300毫升水的温度变化
- 蓝色散点,800毫升水的温度变化
初步观察,3个烧杯水开始温度重合,都是100度。100毫升水随时间变化快,800毫升水随时间变化慢。
3. 程序实现
接下来,分别计算出3种情况下的水温冷却的理论值,通过牛顿冷却定律,并验证理论值与观测值之差的差别,是否能通过理论值来描述测量值。
3.1 用牛顿冷却定律计算100毫升水的温度
计算步骤:
- 计算1分钟内的k值
- 计算每个统计时间的k值,并求平均k值
- 根据平均k值,计算每个统计时间温度
- 对比理论值和测量值,进行可视化
- 计算理论值和测量值的均方根误差
- 进行理论值和测量值的统计检验
- 得出结论
第一步,计算1分钟内的k值。
# 室温 23度
> Ta <- 23
# 根据公式计算k值, k = ln((T(1)-Ta)/(T(0)-Ta))/t1
> k = log((dat$temp_100ml[2]-Ta)/(dat$temp_100ml[1]-Ta)) / dat$time_min[2]
> k
[1] -0.0671393
当t=1时(1分钟),传热系数k值为-0.0671393。
第二步,计算每个统计时间的k值,并求平均k值
# 每个统计时候的k值
> kv = log((dat$temp_100ml[-1]-Ta)/(dat$temp_100ml[1]-Ta)) / dat$time_min[-1]
> kv
[1] -0.06713930 -0.13313399 -0.10615124 -0.10299495 -0.09873156 -0.09326930 -0.08659083
[8] -0.08827741 -0.08447628 -0.08174449 -0.07702708 -0.07581818 -0.07511612 -0.07225721
[15] -0.06986457 -0.06785681 -0.06617233 -0.06476398 -0.06593489 -0.06263815 -0.06187062
[22] -0.06127605 -0.06084202 -0.05830694 -0.05813735 -0.05590129 -0.05594785 -0.05611488
[29] -0.05640535 -0.05452517 -0.05276630 -0.05111735 -0.05165903 -0.05231930 -0.05082446
[36] -0.04864775 -0.04536045 -0.04528728 -0.04359810 -0.04253410
# k平均值
> k<-mean(kv);k
[1] -0.06758501
第三步,根据平均k值,计算每个统计时间温度
# 计算理论温度
> Tt<- Ta + (dat$temp_100ml[1] - Ta)*exp(k*dat$time_min[-1])
> Tt
[1] 94.96792 90.26469 85.86882 81.76024 77.92015 74.33103 70.97645 67.84111 64.91067 62.17173
[11] 59.61179 57.21915 54.98287 52.89273 50.93919 49.11331 47.40676 45.81174 44.32095 42.92759
[21] 41.62529 40.40809 39.27044 38.20714 37.21333 36.28446 35.41630 34.60487 33.84648 33.13764
[31] 32.47513 31.85591 31.27716 30.73624 30.23066 28.15726 26.67841 25.62362 24.87129 24.33470
第四步,对比理论值和测量值,进行可视化
# 把100ml的理论值和测量值合并数据框
> df100<-data.frame(dat[,1:2],Tt=c(100,Tt))
# 进行可视化,测试值为黑色点,理论值为红色线
> plot(df100$time_min,df100$temp_100ml,ylim=c(0,100))
> lines(df100$time_min,df100$Tt,col="red")
第五步,计算理论值和测量值的均方根误差
> sqrt(sum((df100$Tt - df100$temp_100ml)^2)/nrow(df100))
[1] 4.800323
第六步,进行理论值和测量值的统计检验。
对观测值和理论分别进行正常分步的检验,判断是否属于正态分布。
# 观测值检验
> shapiro.test(df100[,2])
Shapiro-Wilk normality test
data: df100[, 2]
W = 0.88026, p-value = 0.0004557
# 理论值检验
> shapiro.test(df100[,3])
Shapiro-Wilk normality test
data: df100[, 3]
W = 0.90219, p-value = 0.001925
通过shapiro-wilk检验,以0.05为显著性水平,p-value都小于0.05,所以拒绝原假设,观测值和预测值都不符合正态分布,也就不能使用T检验和F检验,对数据集是分析了。
卡方检验,用于检验2个独立样本的观测值与期望值的差距。
# 卡方检验
> x <- matrix(c(df100[,2],df100[,3]), ncol = 2)
> chisq.test(x)
Pearson's Chi-squared test
data: x
X-squared = 10.266, df = 40, p-value = 1
以0.05为显著性水平,p-value=1都大于0.05,所以不能拒绝原假设,观测值和理论值没有明显的差异性,用理论值来近似观测值的方法是合理的。
第七步,得出结论,使用牛顿冷却定律进行理论值计算与实际观测值没有明显的差异性,用理论值来近似观测值的方法是合理的,根绝牛顿冷却定律得出的理论值可以作为有效的热传递的计算方法。
再分别计算300毫升水和800毫升水的理论值和观测值之间的关系。
3.2 用牛顿冷却定律计算300毫升水的温度
300毫升水,计算理论值。
# 300毫升水
> kv = log((dat$temp_300ml[-1]-Ta)/(dat$temp_300ml[1]-Ta)) / dat$time_min[-1]
# k均值
> k<-mean(kv);k
[1] -0.0447057
# 计算每个统计时间的温度
> Tt<- Ta + (dat$temp_300ml[1] - Ta)*exp(k*dat$time_min[-1]);Tt
[1] 96.63347 93.41413 90.33555 87.39156 84.57629 81.88411 79.30963 76.84771 74.49342 72.24207
[11] 70.08915 68.03036 66.06159 64.17888 62.37850 60.65682 59.01043 57.43601 55.93043 54.49067
[21] 53.11386 51.79725 50.53820 49.33420 48.18284 47.08182 46.02894 45.02208 44.05925 43.13852
[31] 42.25804 41.41606 40.61089 39.84092 39.10461 35.87873 33.29902 31.23605 29.58630 28.26701
# 合并理论值和观测值
> df300<-data.frame(dat[,c('time_min',"temp_300ml")],Tt=c(100,Tt))
# 均方根误差
> sqrt(sum((df300$Tt - df300$temp_300ml)^2)/nrow(df300))
[1] 3.711398
# 可视化
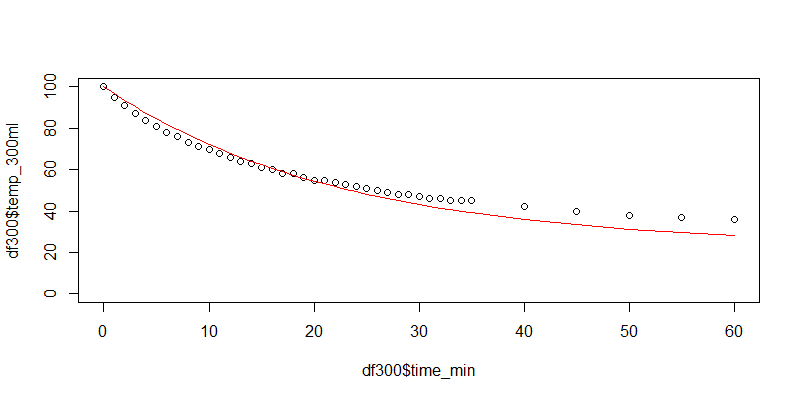
> plot(df300$time_min,df300$temp_300ml,ylim=c(0,100))
> lines(df300$time_min,df300$Tt,col="red")
3.3 用牛顿冷却定律计算800毫升水的温度
800毫升水,计算理论值
> kv = log((dat$temp_800ml[-1]-Ta)/(dat$temp_800ml[1]-Ta)) / dat$time_min[-1]
# k均值
> k<-mean(kv);k
[1] -0.03266545
# 计算每个统计时间的温度
> Tt<- Ta + (dat$temp_800ml[1] - Ta)*exp(k*dat$time_min[-1]);Tt
[1] 97.52540 95.13032 92.81222 90.56862 88.39712 86.29540 84.26123 82.29244 80.38692 78.54263
[11] 76.75762 75.02998 73.35785 71.73947 70.17309 68.65706 67.18974 65.76959 64.39507 63.06473
[21] 61.77714 60.53093 59.32478 58.15738 57.02750 55.93394 54.87552 53.85111 52.85963 51.90001
[31] 50.97123 50.07230 49.20226 48.36018 47.54516 43.84653 40.70523 38.03729 35.77137 33.84689
# 合并理论值和观测值
> df800<-data.frame(dat[,c('time_min',"temp_800ml")],Tt=c(100,Tt))
# 均方根误差
> sqrt(sum((df800$Tt - df800$temp_800ml)^2)/nrow(df800))
[1] 2.237821
# 可视化
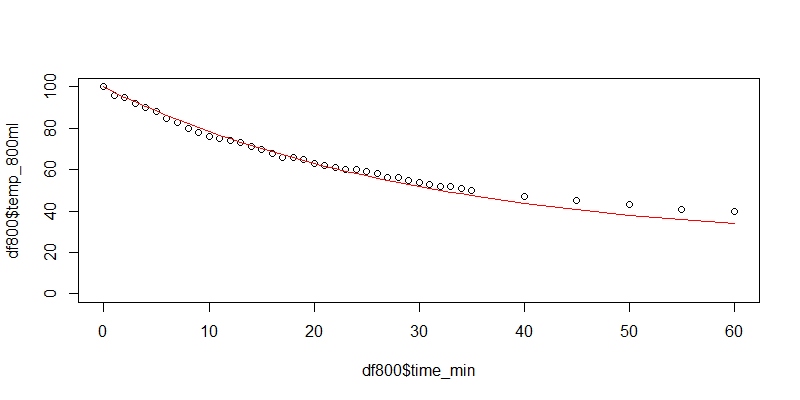
plot(df800$time_min,df800$temp_800ml,ylim=c(0,100))
lines(df800$time_min,df800$Tt,col="red")
3.4 总结
最后,把3种情况的评价指标整理到一起,形成一个表格。
| 水量 | k平均值 | 均方根误差 |
| 100ml | -0.06758501 | 4.800323 |
| 300ml | -0.0447057 | 3.711398 |
| 800ml | -0.03266545 | 2.237821 |
800ml的烧瓶的水,均方根误差最小,理论值与观测值拟合最好;同时,传热系数k值最小,说明水量越多传热越慢。100ml的烧杯的水,均方根误差最大,理论值与观测值拟合最差;同时,传热系数k值最大,说明水量越少传热越快。
牛顿冷却定律是一种热力学模型,通过温度与时间之间的函数关系,构建出了一个指数衰减的过程,这种衰减过程不仅能表达热传导的关系,还被应用到了如新闻热度排名领域。对基础科学的公理和定理的研究,可以极大地开阔研究数据的思路,形成跨学科的解决方案,下篇文章我将介绍牛顿冷却定律在基于用户投票的排名算法场景中的应用。
转载请注明出处:
http://blog.fens.me/r-newton-cooling