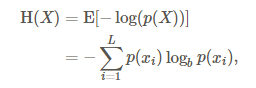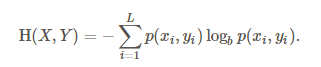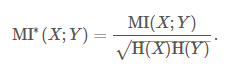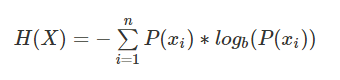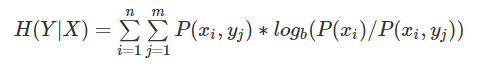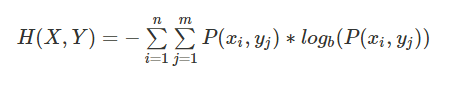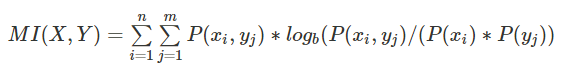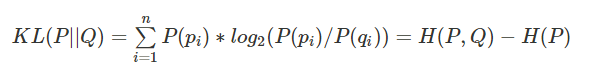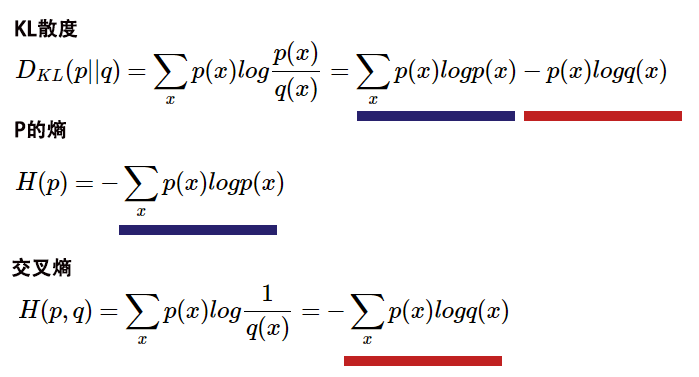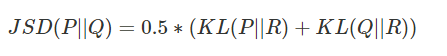R的极客理想系列文章,涵盖了R的思想,使用,工具,创新等的一系列要点,以我个人的学习和体验去诠释R的强大。
R语言作为统计学一门语言,一直在小众领域闪耀着光芒。直到大数据的爆发,R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入,R语言的社区在迅速扩大成长。现在已不仅仅是统计领域,教育,银行,电商,互联网….都在使用R语言。
要成为有理想的极客,我们不能停留在语法上,要掌握牢固的数学,概率,统计知识,同时还要有创新精神,把R语言发挥到各个领域。让我们一起动起来吧,开始R的极客理想。
关于作者:
- 张丹(Conan), 程序员/Quant: Java,R,Nodejs
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-entropy-muti
前言
信息熵作为信息度量的基础,被广泛的算法模型所使用,比如决策树,熵值法等,基于信息熵的扩展我们可以做很多的事情。
本文将给大家介绍一个新模型思路,用信息熵来衡量具有时间特征的两随机变量的信息差。由Mark D. Scheuerell教授开发,所属美国西雅图西雅图国家海洋和大气管理局,国家海洋渔业局西北渔业科学中心,鱼类生态学部。
目录
- muti包介绍
- muti包函数定义
- muti包使用
- 实战案例
1. muti包介绍
muti包是用于计算两个离散随机变量之间的互信息(MI)的R包。 muti包设计目标,是考虑时间序列分析的情况下开发的,但没有任何方法可以将方法与时间索引本身联系起来。
muti项目的主页:https://mdscheuerell.github.io/muti/
熵是用来含量信息的单位,我在文章 用R语言实现信息度量 中已有详细介绍。那么,通过计算两随机变量的互信息,来估计一个变量中包含的另一个变量的信息量,可以理解为是两个变量之间协方差的非参数度量。
muti包中用来计算互信息的计算过程,包括以下几步:
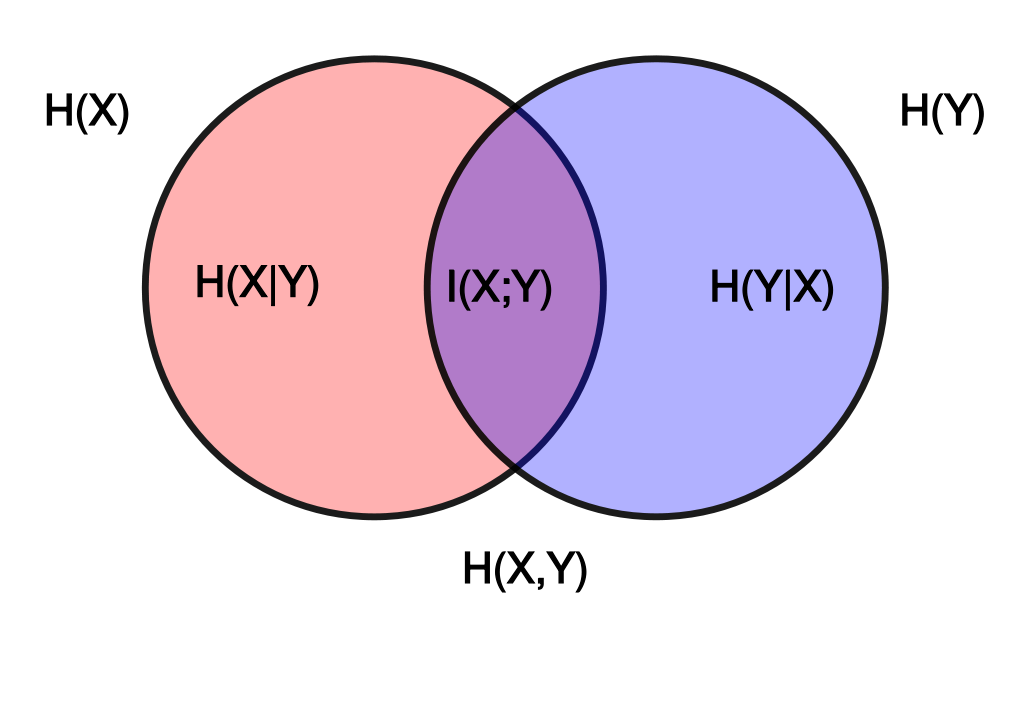
第一步,计算信息熵H(x),H(y):
第二步,计算联合熵H(x,y):
第三步,计算互信息MI(x;y):
第四步,标准化互信息,映射到[0,1]区间:
开发环境所使用的系统环境
- Win10 64bit
- R: 3.4.2 x86_64-w64-mingw32/x64 b4bit
muti目前还没有发布到CRAN上面,需要通过devtools包从github上进行安装。安装操作如下。
> if(!require("devtools")) {
> install.packages("devtools")
> library("devtools")
> }
> devtools::install_github("mdscheuerell/muti")
2. muti包函数定义
muti包,有很强的专业性,没有太多的函数定义,函数都是为了实现模型的算法。
- muti(),主函数,用于计算两个向量的互信息并画图输出
- mutual_info(),计算互信息
- newZ(),基于原始数据的重新采样创建新矢量。
- symbolize(),将数字向量转换为符号向量。
- transM(),估计用于计算互信息上的临界阈值的转换矩阵。
- plotMI(),画图输出
2.1 muti()函数:
主函数,用于计算两个向量的互信息并画图输出。
函数定义:
muti(x, y, sym = TRUE, n_bins = NULL, normal = FALSE, lags = seq(-4, 4), mc = 100, alpha = 0.05)
参数列表:
- x, 向量
- y, 向量
- sym,是否转换成符号向量,默认TRUE,
- n_bins, 离散化方法,当sym=FALSE时, n_bins = ceiling(2 * length(x)^(1/3))
- normal, 是否标准化,默认FALSE
- lags, 滞后周期,默认为seq(-4, 4)
- mc, 用于估计互信息的临界阈值的蒙特卡洛数量的模拟,默认100,
- alpha, 用于定义临界阈值的取值点0.05
2.2 mutual_info()函数:
计算互信息,源函数的定义过于复杂,我重新进行的优化,使得结构简单易懂。
# 源函数
mutual_info <- function(su,normal) {
## function to calculate mutual information between 2 time series
## need to remove obs with NA's b/c they don't contribute to info
su <- su[!apply(apply(su,1,is.na),2,any),]
## get number of bins
bb <- max(su)
## get ts length
TT <- dim(su)[1]
## init entropies
H_s <- H_u <- H_su <- 0
for(i in 1:bb) {
## calculate entropy for 1st series
p_s <- sum(su[,1] == i)/TT
if(p_s != 0) { H_s <- H_s - p_s*log(p_s, 2) }
## calculate entropy for 2nd series
p_u <- sum(su[,2] == i)/TT
if(p_u != 0) { H_u <- H_u - p_u*log(p_u, 2) }
for(j in 1:bb) {
## calculate joint entropy
p_su <- sum(su[,1]==i & su[,2]==j)/TT
if(p_su != 0) { H_su <- H_su - p_su*log(p_su, 2) }
} ## end j loop
} ## end i loop
## calc mutual info
MI <- H_s + H_u - H_su
if(!normal) { return(MI) } else { return(MI/sqrt(H_s*H_u)) }
}
# 修改后的函数
library(philentropy)
mutual_info <- function(su,normal){
n<-nrow(su)
px<-table(su[,1])/n
py<-table(su[,2])/n
hX<-H(px)
hY<-H(py)
tf<-table(su[,1],su[,2])
pXY<-prop.table(tf)
hXY<-JE(pXY)
MI<-hX+hY-hXY
if(normal){
return(MI/sqrt(hX * hY))
}else{
return(MI)
}
}
2.3 symbolize()函数:
将数字向量转换为符号向量,同样源函数定义过于复杂,我重写了一下。
# 源函数
symbolize <- function(xy) {
## of interest and converts them from numeric to symbolic.
## check input for errors
if(dim(xy)[2] != 2) {
stop("xy must be an [n x 2] matrix \n\n", call.=FALSE)
}
## get ts length
TT <- dim(xy)[1]
## init su matrix
su <- matrix(NA, TT, 2)
## convert to symbols
## loop over 2 vars
for(i in 1:2) {
for(t in 2:(TT-1)) {
## if xy NA, also assign NA to su
if(any(is.na(xy[(t-1):(t+1),i]))) { su[t,i] <- NA }
## else get correct symbol
else {
if(xy[t,i] == xy[t-1,i] & xy[t,i] == xy[t+1,i]) {
## same
su[t,i] <- 3
}
if(xy[t,i] > xy[t-1,i]) {
## peak
if(xy[t,i] > xy[t+1,i]) { su[t,i] <- 5 }
## increase
else { su[t,i] <- 4 }
}
if(xy[t,i] < xy[t-1,i]) {
## trough
if(xy[t,i] < xy[t+1,i]) { su[t,i] <- 1 }
## decrease
else { su[t,i] <- 2 }
}
} ## end else
} ## end t loop
} ## end i loop
## return su matrix
return(su)
}
# 优化后的函数
symbolize<-function(xy){
if(ncol(xy)!=2) {
stop("xy must be an [n x 2] matrix \n\n", call. = FALSE)
}
idx<-2:(nrow(xy)-1)
apply(xy,2,function(row){
na<-which(is.na(row[idx]+row[idx-1]+row[idx+1]))
n3<-which(row[idx]==row[idx-1] & row[idx]==row[idx+1])
n5<-which(row[idx]>row[idx-1] & row[idx]>row[idx+1])
n4<-which(row[idx]>row[idx-1] & row[idx]<=row[idx+1])
n1<-which(row[idx]<row[idx-1] & row[idx]<row[idx+1])
n2<-which(row[idx]<row[idx-1] & row[idx]>=row[idx+1])
line<-rep(0,length(idx))
line[na]<-NA
line[n1]<-1
line[n2]<-2
line[n3]<-3
line[n4]<-4
line[n5]<-5
c(NA,line,NA)
})
}
2.4 transM()函数:
估计用于计算互信息上的临界阈值的转换矩阵,同样源函数定义过于复杂,我重写了一下。
# 源函数
transM <- function(x,n_bins) {
## helper function for estimating transition matrix used in
## creating resampled ts for the CI on mutual info
## replace NA with runif()
x[is.na(x)] <- runif(length(x[is.na(x)]),min(x,na.rm=TRUE),max(x,na.rm=TRUE))
## length of ts
tt <- length(x)
## get bins via slightly extended range
bins <- seq(min(x)-0.001,max(x),length.out=n_bins+1)
## discretize ts
hin <- vector("numeric",tt)
for(b in 1:n_bins) {
hin[x > bins[b] & x <= bins[b+1]] <- b
}
## matrix of raw-x & discrete-x
xn <- cbind(x,hin)
## transition matrix from bin-i to bin-j
MM <- matrix(0,n_bins,n_bins)
for(i in 1:n_bins) {
for(j in 1:n_bins) {
MM[i,j] <- sum(hin[-tt]==i & hin[-1]==j)
}
if(sum(MM[i,])>0) { MM[i,] <- MM[i,]/sum(MM[i,]) }
else { MM[i,] <- 1/n_bins }
}
return(list(xn=xn,MM=MM))
} ## end function
# 优化后的函数
transM <- function(x,n_bins){
x[is.na(x)] <- runif(length(x[is.na(x)]), min(x, na.rm = TRUE),max(x, na.rm = TRUE))
n<-length(x)
xn<-cbind(x,hin=cut(x,7))
hin<-xn[,2]
a<-data.frame(id=1:(n-1),a=hin[1:(n-1)])
b<-data.frame(id=1:(n-1),b=hin[2:n])
ab<-merge(a,b,by="id",all=TRUE)
ab$v<-1
abm<-aggregate(v~a+b,data=ab,sum)
MM <- matrix(0, n_bins, n_bins)
apply(abm,1,function(row){
MM[row[1],row[2]]<<-row[3]
invisible()
})
MN<-apply(MM,1,function(row){
s<-sum(row)
if(s>0){
row/s
}else{
rep(1/n_bins,n_bins)
}
})
MN<-t(MN)
return(list(xn = xn, MM = MN))
}
由于作者的代码,是以it的逻辑写的,其实并不太符合数据计算的逻辑,我用向量化代码对源代码进行了优化,使用算法逻辑更清晰一下,同时我也上传到了github:https://github.com/bsspirit/muti
3. muti包使用
接下来,就是对muti包的使用了,作者提供了一个实例给我们做参考。
3.1 数据的输入和输出
muti()函数,是muti包的主函数,调用muti()就完成了这个包的全部功能。
- 输入,要求是2个数字型向量。
- 输出,包括了2个部分,1.数据计算结果,2.可视化的结果。
新建一个程序
> set.seed(123)
> TT <- 30
# 创建两个数字型向量
> x1 <- rnorm(TT)
> y1 <- x1 + rnorm(TT)
# 计算互信息
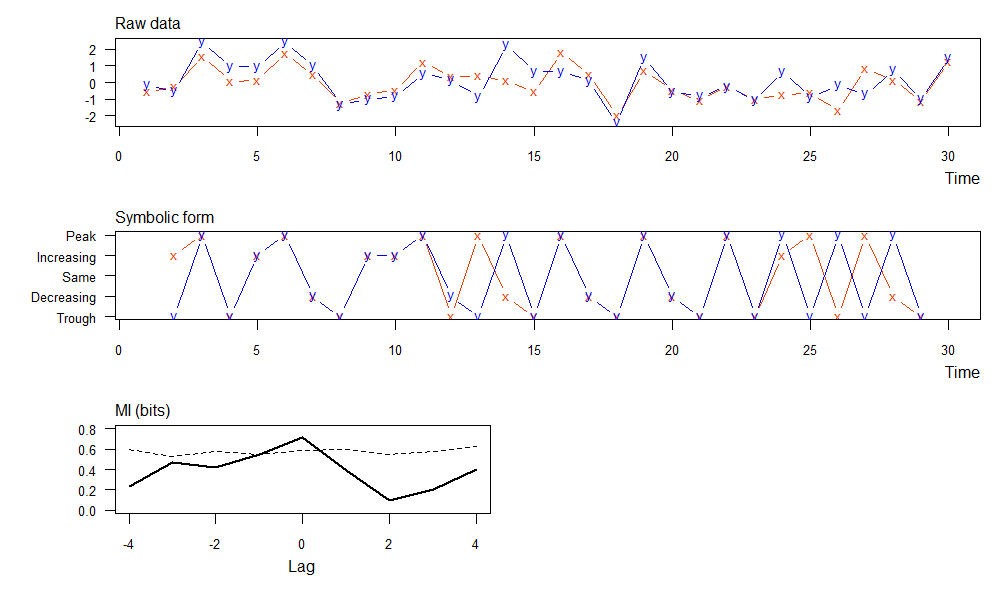
> muti(x1, y1)
lag MI_xy MI_tv
1 -4 0.238 0.595
2 -3 0.473 0.532
3 -2 0.420 0.577
4 -1 0.545 0.543
5 0 0.712 0.584
6 1 0.393 0.602
7 2 0.096 0.546
8 3 0.206 0.573
9 4 0.403 0.625
数据计算结果,包括3列:
- lag: 滞后期,当lag=-1,length(x)=length(y)=26时,x取值[1:25],y取值[2:26];当lag=1,length(x)=length(y)=26时,x取值[2:26],y取值[1:25];
- MI_xy: 互信息
- MI_tv: 相应显着性阈值,用蒙特卡洛方法生成互信息,按从大到小排序后取1-alpha位置的值。
- 上图,原始数据的x,y两个变量
- 中图,符号转型后的x,y两个变量,把原始数据离散化为5个值,差异化更大
- 下图,滞后期的互信息(实线)和相应显着性阈值(虚线),同数据计算结果的输出。
3.2 离散化处理
在计算信息熵时,muti包是将源数据进行了离散化处理,通过离散化进行分组,计算不同分组的概率矩阵,从而得出互信息。
muti包提供了2种离散化。
- 符号化: 把连续型的数据,映射到5个值的上,分别对应peak(峰值), increasing(增加), same(没变),decreasing(减少),trough(低谷)。比如,向量c(1.1,2.1,3.3,1.2,3.1),不计算第一个值和最后一个值,第二个值2.1>第一个值1.1,第二个值2.1<第三个值3.3时,第二个值为增加。第2,3,4值,分别为c(“增加”,“峰值”,“低谷”)。
- 分箱法: 等宽分箱,如果没有指定箱数,则根据莱斯规则计算,其中n = ceiling(2*length(x)^(1/3))。
4. 实战案例
利用muti的模型特点,我们取一组金融市场的数据进行分析,满足x和y是两个连续型变量,同时x和y之间有一些在金融市场上有一定的关系,通过分析x对y的确定性的贡献度来解释互信息值的合理性。
我们取中国A股市场上证综指(000001.SH)和工商银行(601398.SH)的每日收盘价的向前复权的数据,从2014-10-21到2018-12-31。工商银行是上证综指的权重股,所以让x=工商银行,y=上证综指,通过计算互信息来验证工商银行能够给上证综指带来多少确定性的信息增益。
整个案例部分的代码,有多处省略,并不影响阅读和分析。如果需要代码的朋友,请扫文章下面的二维码,请作者喝杯咖啡。
整理来xts类型的时间序列数据,数据格式如下:
// 省略部分代码
> head(stock,20)
date X601398 X000001
1 2014-10-21 2.92 2339.66
2 2014-10-22 2.91 2326.55
3 2014-10-23 2.92 2302.42
4 2014-10-24 2.92 2302.28
5 2014-10-27 2.90 2290.44
6 2014-10-28 2.92 2337.87
7 2014-10-29 2.94 2373.03
8 2014-10-30 2.98 2391.08
9 2014-10-31 3.04 2420.18
10 2014-11-03 3.01 2430.03
11 2014-11-04 3.02 2430.68
12 2014-11-05 2.97 2419.25
13 2014-11-06 2.97 2425.86
14 2014-11-07 2.97 2418.17
15 2014-11-10 3.05 2473.67
16 2014-11-11 3.16 2469.67
17 2014-11-12 3.12 2494.48
18 2014-11-13 3.12 2485.61
19 2014-11-14 3.14 2478.82
20 2014-11-17 3.11 2474.01
3列数据,第一列是时间列,第二列是X601398人收盘价,第三列是X000001收盘价。从价格上看,2个数据集并不在同一个度量内,我们转化度量单位为每日收益率。
数据变型后,每日收益率结果如下:
> head(ret,20)
X601398 X000001
2014-10-21 NA NA
2014-10-22 -0.003424658 -5.603378e-03
2014-10-23 0.003436426 -1.037158e-02
2014-10-24 0.000000000 -6.080559e-05
2014-10-27 -0.006849315 -5.142728e-03
2014-10-28 0.006896552 2.070781e-02
2014-10-29 0.006849315 1.503933e-02
2014-10-30 0.013605442 7.606309e-03
2014-10-31 0.020134228 1.217023e-02
2014-11-03 -0.009868421 4.069945e-03
2014-11-04 0.003322259 2.674864e-04
2014-11-05 -0.016556291 -4.702388e-03
2014-11-06 0.000000000 2.732252e-03
2014-11-07 0.000000000 -3.170010e-03
2014-11-10 0.026936027 2.295124e-02
2014-11-11 0.036065574 -1.617031e-03
2014-11-12 -0.012658228 1.004588e-02
2014-11-13 0.000000000 -3.555851e-03
2014-11-14 0.006410256 -2.731724e-03
2014-11-17 -0.009554140 -1.940439e-03
然后,我们把每日收益率转换为累积收益率,让收益曲线为连续值,这样就构建好了,muti模型需要的输入数据。
> head(rdf,20)
X601398 X000001
2014-10-22 -0.003424658 -0.0056033783
2014-10-23 0.000000000 -0.0159168426
2014-10-24 0.000000000 -0.0159766804
2014-10-27 -0.006849315 -0.0210372447
2014-10-28 0.000000000 -0.0007650684
2014-10-29 0.006849315 0.0142627561
2014-10-30 0.020547945 0.0219775523
2014-10-31 0.041095890 0.0344152569
2014-11-03 0.030821918 0.0386252703
2014-11-04 0.034246575 0.0389030885
2014-11-05 0.017123288 0.0340177633
2014-11-06 0.017123288 0.0368429601
2014-11-07 0.017123288 0.0335561577
2014-11-10 0.044520548 0.0572775531
2014-11-11 0.082191781 0.0555679030
2014-11-12 0.068493151 0.0661720079
2014-11-13 0.068493151 0.0623808588
2014-11-14 0.075342466 0.0594787277
2014-11-17 0.065068493 0.0574228734
2014-11-18 0.058219178 0.0498833164
取前50个点,把x和y带入muti()函数。
> x<-rdf$X601398
> y<-rdf$X000001
> result<-muti(x,y)
> result
lag MI_xy MI_tv
1 -4 0.148 0.534
2 -3 0.158 0.464
3 -2 0.190 0.385
4 -1 0.351 0.425
5 0 0.646 0.398
6 1 0.528 0.340
7 2 0.262 0.461
8 3 0.207 0.437
9 4 0.260 0.518
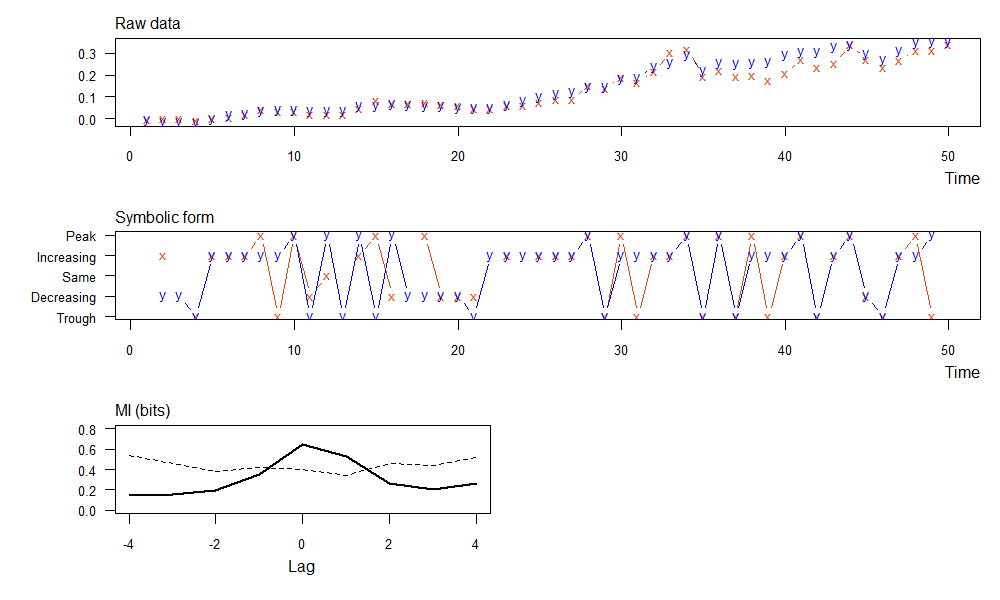
- 上图,为原始数据的x(上证综指)和y(工商银行)的累积收益率曲线。
- 中图,为符号转型后的x(上证综指)和y(工商银行)的累积收益率曲线。
- 下图,符号转型后的数据,滞后期从-4到4的9个的互信息(实线)和和相应显着性阈值(虚线)。
当滞后期为lag=0时,MI互信息最大为0.646,表示工商银行给上证综指带来的信息是最确定的。而当有不同的滞后期时,MI互信息都为小,表示工商银行给上证综指的信息确定性变小了。
这个结果是符合金融市场的业务规则的。工商银行是上证综指的权重股,工商银行的当天股价的走势是会影响当天的上证综指的走势的,但是并不会影响上证综指前一天或第二天的走势,所以得到的结果是符合逻辑的。
另外,我们再引入一个统计变量进行验证。假设越2组数据越确定,那么2组数据的差值的标准差应该是越小,差异越大则标准差越大,然后再进行验证。
输出数据集为4列,最后一列增加了标准差(sd)。
// 省略部分代码
> rsdf
lag MI_xy MI_tv sd
1 -4 0.148 0.534 1.991886
2 -3 0.158 0.464 2.400721
3 -2 0.190 0.385 2.107189
4 -1 0.351 0.425 2.378768
5 0 0.646 0.398 1.477030
6 1 0.528 0.340 2.342482
7 2 0.262 0.461 1.997676
8 3 0.207 0.437 2.267211
9 4 0.260 0.518 2.116934
从数据可以看出,第5行当lag=0时,sd=1.477是最小的,说明这个时候,2组数据的差异是最小的,而其他的时候sd都比较大。我们再有可视化进行输出。
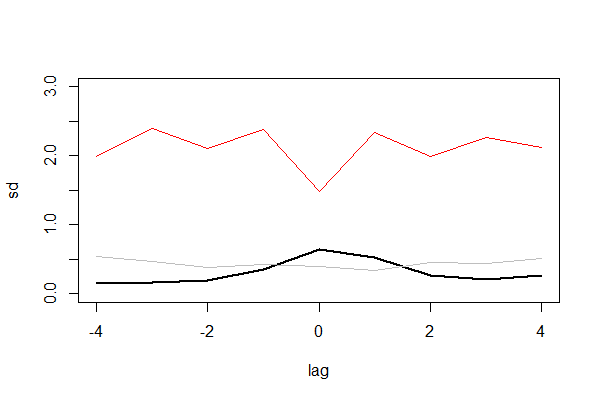
图中有3条线,黑实线为互信息,灰色线为阈值,红色线为标准差。这样就更直观地看出,标准化的曲线和互信息的曲线刚好相反。当差异越小时,标准差越小,互信息越大,x对y的确定性越大。这样就证明了,muti包也是适合用在金融市场的模型。
虽然本案例没有使用模型构建策略生成交易信号,但论证了模型的可行性和正确性。大家可以基于文章的思路,找到适合的场景进行策略应用,比如跨期套利或跨品种套利时,2种不同合约之间的确定性的依赖程度,来形成交易策略。
我们完成对muti包的解读,使用,测试,验证的全过程。通过新的模型思路,获得新的知识,才能在金融市场上有更多的机会,从而突破信息相同,技术工具相同等的白热化竞争环境。
整个案例部分的代码,有多处省略,并不影响阅读和分析。如果需要代码的朋友,请扫文章下面的二维码,请作者喝杯咖啡。
转载请注明出处:
http://blog.fens.me/r-entropy-muti