R的极客理想系列文章,涵盖了R的思想,使用,工具,创新等的一系列要点,以我个人的学习和体验去诠释R的强大。
R语言作为统计学一门语言,一直在小众领域闪耀着光芒。直到大数据的爆发,R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入,R语言的社区在迅速扩大成长。现在已不仅仅是统计领域,教育,银行,电商,互联网….都在使用R语言。
要成为有理想的极客,我们不能停留在语法上,要掌握牢固的数学,概率,统计知识,同时还要有创新精神,把R语言发挥到各个领域。让我们一起动起来吧,开始R的极客理想。
关于作者:
- 张丹(Conan), 程序员/Quant: Java,R,Nodejs
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-cluster-kmeans
前言
聚类属于无监督学习中的一种方法,k-means作为数据挖掘的十大算法之一,是一种最广泛使用的聚类算法。我们使用聚类算法将数据集的点,分到特定的组中,同一组的数据点具有相似的特征,而不同类中的数据点特征差异很大。PAM是对k-means的一种改进算法,能降低异常值对于聚类效果的影响。
聚类可以帮助我们认识未知的数据,发现新的规律。
目录
- k-means实现
- PAM实现
- 可视化和段剖面图
1. k-means实现
k-means算法,是一种最广泛使用的聚类算法。k-means以k作为参数,把数据分为k个组,通过迭代计算过程,将各个分组内的所有数据样本的均值作为该类的中心点,使得组内数据具有较高的相似度,而组间的相似度最低。
k-means工作原理:
- 初始化数据,选择k个对象作为中心点。
- 遍历整个数据集,计算每个点与每个中心点的距离,将它分配给距离中心最近的组。
- 重新计算每个组的平均值,作为新的聚类中心。
- 上面2-3步,过程不断重复,直到函数收敛,不再新的分组情况出现。
k-means聚类,适用于连续型数据集。在计算数据样本之间的距离时,通常使用欧式距离作为相似性度量。k-means支持多种距离计算,还包括maximum, manhattan, pearson, correlation, spearman, kendall等。各种的距离算法的介绍,请参考文章R语言实现46种距离算法
1.1 kmeans()函数实现
在R语言中,我们可以直接调用系统中自带的kmeans()函数,就可以实现k-means的聚类。同时,有很多第三方算法包也提供了k-means的计算函数。当我们需要使用kmeans算法,可以使用第三方扩展的包,比如flexclust, amap等包。
本文的系统环境为:
- Win10 64bit
- R: 3.4.4 x86_64-w64-mingw32
接下来,让我们做一个k-means聚类的例子。首先,创建数据集。
# 创建数据集
> set.seed(0)
> df <- rbind(matrix(rnorm(100, 0.5, 4.5), ncol = 2),
+ matrix(rnorm(100, 0.5, 0.1), ncol = 2))
> colnames(df) <- c("x", "y")
> head(df)
x y
[1,] 6.1832943 1.6976181
[2,] -0.9680501 -1.1951622
[3,] 6.4840967 11.4861408
[4,] 6.2259319 -3.0790260
[5,] 2.3658865 0.2530514
[6,] -6.4297752 1.6256360
使用stats::kmeans()函数,进行聚类。
> cl <- kmeans(df,2); cl
K-means clustering with 2 clusters of sizes 14, 86
Cluster means: # 中心点坐标
x y
1 5.821526 2.7343127
2 -0.315946 0.1992429
Clustering vector: # 分组的索引
[1] 1 2 1 1 2 2 2 2 2 1 1 2 2 2 2 2 2 2 2 2 2 2 2 1 2 1 1 2 2 2 2 2 2 2 2 1 1 2 1 2 1 2 2 2 2 2 2 1 1 2
[51] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
Within cluster sum of squares by cluster:
[1] 316.0216 716.4009 # withinss,分组内平方和
(between_SS / total_SS = 34.0 %) # 组间的平方和/总平方和,用于衡量点聚集程度
Available components: # 对象属性
[1] "cluster" "centers" "totss" "withinss" "tot.withinss" "betweenss"
[7] "size" "iter" "ifault"
# 查看数据分组情况,第1组86个,第2组14个
> cl$size
[1] 86 14
对象属性解读:
- cluster,每个点的分组
- centers,聚类的中心点坐标
- totss,总平方和
- withinss,每个分组内的平方和
- tot.withinss,分组总和,sum(withinss)
- betweenss,组间的平方和,totss – tot.withinss
- size,每个组中的数据点数量
- iter,迭代次数。
- ifault,可能有问题的指标
1.2 kcca()函数实现
我们再使用flexclust::kcca()函数,进行聚类。
# 安装flexclust包
> # install.packages("flexclust")
> library(flexclust)
# 进行聚类
> clk<-kcca(df,k=2);clk
kcca object of family ‘kmeans’
call:
kcca(x = df, k = 2)
cluster sizes: # 聚类的分组大小
1 2
84 16
# 聚类的中心
> clk@centers
x y
[1,] -0.3976465 0.2015319
[2,] 5.4832702 2.4054118
# 查看聚类的概览信息
> summary(clk)
kcca object of family ‘kmeans’
call:
kcca(x = df, k = 2)
cluster info: # 每个组的基本信息,包括分组数量,平均距离、最大距离、分割值
size av_dist max_dist separation
1 84 2.102458 9.748136 3.368939
2 16 3.972920 9.576635 3.189891
convergence after 5 iterations # 5次迭代
sum of within cluster distances: 240.1732 # 聚类距离之和
我们比较2个不同包的k-means算法,所得到的分组数据都是一样的,中心点位置略有一点偏差。接下来,我们可以把聚类画图。
> plot(df, col = cl$cluster, main="Kmeans Cluster")
> points(cl$centers, col = 1:3, pch = 10, cex = 4) # 画出kmeans()函数效果
从上图中看到k-means的总分2组,每个组的中心点分别用红色十字圆圈和黑色十字圆圈表示,为组内的所有数据样本的均值。再叠加上kcca()函数聚类后的中心点画图。
> points(clk@centers, col = 3:4, pch = 10, cex = 4) # 画出kcca()函数效果
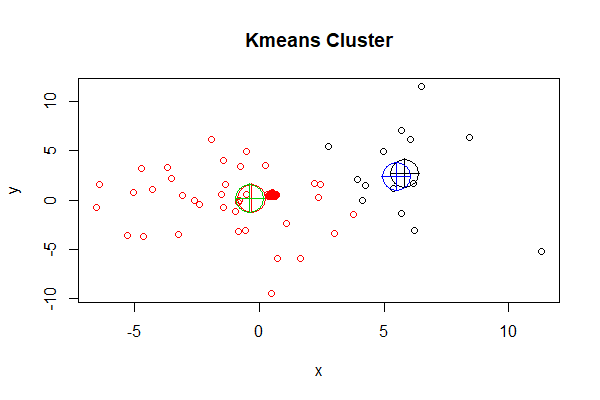
新的中心点,分别用别用绿色十字圆圈和蓝色十字圆圈表示。虽然我们使用了相同的算法,分组个数也相同,但中心点还有一些不同的。
这里其实就要对聚类的稳定性进行判断了,有可能是聚类迭代次数过少,就会出现不同的聚类结果,就需要增加迭代次数,达到每次计算结果是一致的。也有可能是因为不同的包,实现的代码有所区别导致的。
k-means算法,也有一些缺点就是对于孤立点是敏感的,会被一些极端值影响聚类的效果。一种改进的算法是PAM,用于解决这个问题。PAM不使用分组平均值作为计算的参照点,而是直接使用每个组内最中心的对象作为中心点。
2. PAM实现
PAM(Partitioning Around Medoids),又叫k-medoids,它可以将数据分组为k个组,k为数量是要事前定义的。PAM与k-means一样,找到距离中心点最小点组成同一类。PAM对噪声和异常值更具鲁棒性,该算法的目标是最小化对象与其最接近的所选对象的平均差异。PAM可以支持混合的数据类型,不仅限于连续变量。
PAM算法分为两个阶段:
- 第1阶段BUILD,为初始集合S选择k个对象的集合。
- 第2阶段SWAP,尝试用未选择的对象,交换选定的中心点,来提高聚类的质量。
PAM的工作原理:
- 初始化数据集,选择k个对象作为中心。
- 遍历数据点,把每个数据点关联到最近中心点m。
- 随机选择一个非中心对象,与中心对象交换,计算交换后的距离成本
- 如果总成本增加,则撤销交换的动作。
- 上面2-4步,过程不断重复,直到函数收敛,中心不再改变为止。
优点与缺点:
- 消除了k-means算法对于孤立点的敏感性。
- 比k-means的计算的复杂度要高。
- 与k-means一样,必须设置k的值。
- 对小的数据集非常有效,对大数据集效率不高。
在R语言中,我们可以通过cluster包来使用pam算法函数。cluster包的安装很简单,一条命令就安装完了。
> install.packages("cluster")
> library(cluster)
pam()函数定义:
pam(x, k, diss = inherits(x, "dist"), metric = "euclidean",
medoids = NULL, stand = FALSE, cluster.only = FALSE,
do.swap = TRUE,
keep.diss = !diss && !cluster.only && n < 100,
keep.data = !diss && !cluster.only,
pamonce = FALSE, trace.lev = 0)
参数列表:
- x,数据框或矩阵,允许有空值(NA)
- k,设置分组数量
- diss,为TRUE时,x为距离矩阵;为FALSE时,x是变量矩阵。默认为FALSE
- metric,设置距离算法,默认为euclidean,距离矩阵忽略此项
- medoids,指定初始的中心,默认为不指定。
- stand,为TRUE时进行标准化,距离矩阵忽略此项。
- cluster.only,为TRUE时,仅计算聚类结果,默认为FALSE
- do.swap,是否进行中心点交换,默认为TRUE;对于超大的数据集,可以不进行交换。
- keep.diss,是否保存距离矩阵数据
- keep.data,是否保存原始数据
- pamonce,一种加速算法,接受值为TRUE,FALSE,0,1,2
- trace.lev,日志打印,默认为0,不打印
我们使用上面已创建好的数据集df,进行pam聚类,设置k=2。
> kclus <- pam(df,2)
# 查看kclus对象
> kclus
Medoids: # 中心点
ID x y
[1,] 27 5.3859621 1.1469717
[2,] 89 0.4130217 0.4798659
Clustering vector: # 分组
[1] 1 2 1 1 2 2 2 2 2 1 1 2 2 2 2 2 2 2 2 2 2 2 2 1 2 1 1 2 2 2 2 2 2 2 1 1 1 2 1 2 1 2 2 2 2 2 2 1 1 2
[51] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
Objective function: # 目标函数的局部最小值
build swap
2.126918 2.124185
Available components: # 聚类对象的属性
[1] "medoids" "id.med" "clustering" "objective" "isolation" "clusinfo" "silinfo"
[8] "diss" "call" "data"
> kclus$clusinfo # 聚类的分组数量,每个组的平均距离、最大距离、分割值
size max_diss av_diss diameter separation
[1,] 15 10.397323 4.033095 17.35984 1.556862
[2,] 85 9.987604 1.787318 15.83646 1.556862
属性解读:
- medoids,中心点的数据值
- id.med,中心点的索引
- clustering,每个点的分组
- objective,目标函数的局部最小值
- isolation,孤立的聚类(用L或L*表示)
- clusinfo,每个组的基本信息
- silinfo,存储各观测所属的类、其邻居类以及轮宽(silhouette)值
- diss,不相似度
- call,执行函数和参数
- data,原始数据集
把聚类画图输出。
# 画图
> plot(df, col = kclus$clustering, main="Kmedoids Cluster")
> points(kclus$medoids, col = 1:3, pch = 10, cex = 4)
图中,PAM聚类后分为2组,红色一组,黑色一组,用十字圆圈表示2个中心点,可以清晰地看到中心点就是数据点。
我们可以在开始计算时,设置聚类的中心点,为索引1,2坐标点,打印聚类的日志,查看计算过程。
# 设置聚类的中心为1,2
> kclus2<-pam(df,2,medoids=c(1,2),trace.lev=20)
C pam(): computing 4951 dissimilarities from 100 x 2 matrix: [Ok]
pam()'s bswap(*, s=21.837, pamonce=0): medoids given
after build: medoids are 1 2
and min.dist dysma[1:n] are
0 0 9.79 4.78 3.63 6.15 5.23 0.929 8.44 8.59
2.29 2.69 4.48 1.19 1.98 2.81 5.39 4.2 3.72 4.56
1.84 3.99 2.4 2.7 4.84 5.08 0.969 2.01 4.94 5.06
1.94 7.4 5.19 1.62 3.94 3.12 3.51 0.65 4.46 4.61
5.16 4.57 1.82 3.21 5.79 4.01 5.59 5.38 1.95 6.2
2.41 2.09 2.2 2.43 2.24 2.26 2.09 2.39 2.21 2.33
2.24 2.14 2.45 2.37 2.2 2.37 2.13 2.33 2.25 2.18
2.38 2.19 2.15 2.14 2.1 2.39 2.24 2.24 2.12 2.14
2.34 2.18 2.25 2.26 2.33 2.17 2.18 2.12 2.17 2.27
2.29 2.26 2.38 2.12 2.25 2.33 2.09 2.21 2.24 2.13
swp new 89 <-> 2 old; decreasing diss. 306.742 by -93.214
swp new 27 <-> 1 old; decreasing diss. 213.528 by -1.10916
end{bswap()}, end{cstat()}
# 查看中心
> kclus2$id.med
[1] 27 89
通过日志查看,我们可以清楚地看到,2个中心的选择过程,分别用89替换1,距离成本减少93.214,用27替换2,距离成本减少1.1。
PAM作为k-means的一种改进算法,到底结果是否更合理,还要看最终哪种结果能够准确地表达业务的含义,被业务人员所认可,就需要不断地和业务人员来沟通。
3. 可视化和段剖面图
我们实现了聚类计算后,通常需要把复杂的数据逻辑,用简单的语言和图形来解释给业务人员,聚类的可视化就很重要的。如果数据量不太大,参与聚类的指标维度不太多的时候,我们可以用2维散点图,把指标两两画出来。
我们对iris数据集,进行k-means聚类分成3组,画出聚类后的2维散点图结果。
> res <- kmeans(iris[,1:4], centers=3)
> pairs(iris, col = res$cluster + 1)
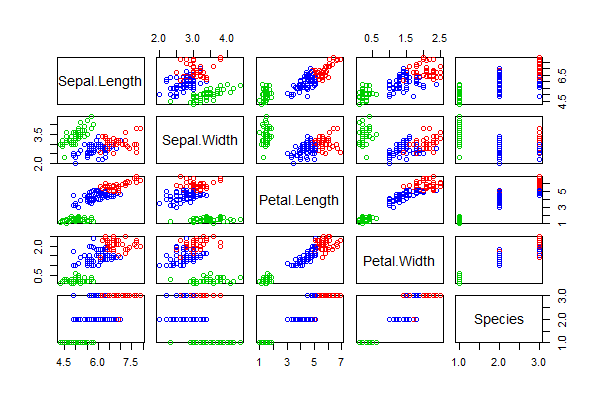
每2个维度就会生成一张图, 我们可以全面直观的看到聚类的效果。
高级画图工具,使用GGally包中的ggpairs()函数。
> library(GGally)
> ggpairs(iris,columns = 1:5,mapping=aes(colour=as.character(res$cluster)))
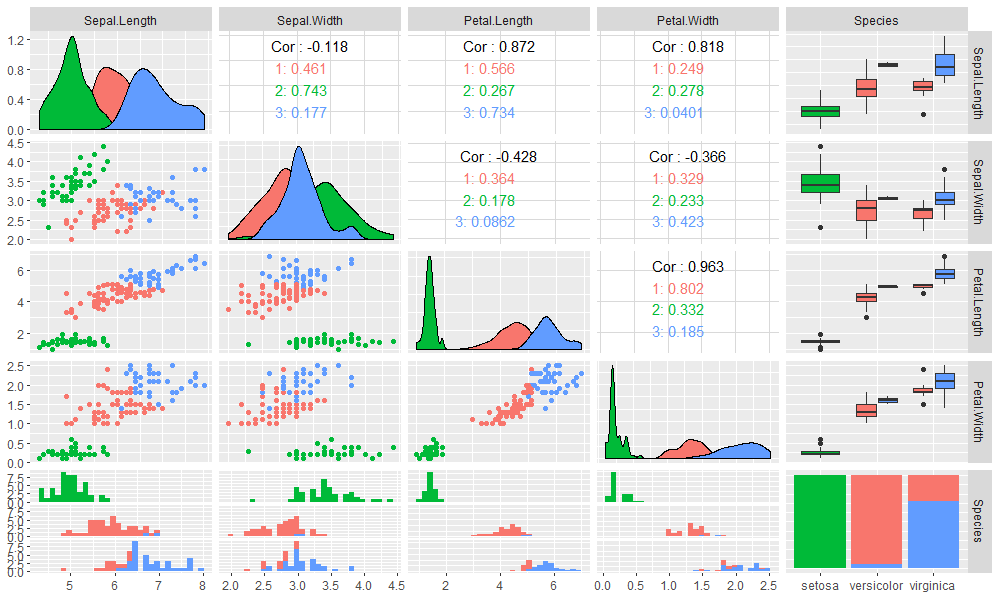
图更漂亮了而且包含更多的信息,除了2维散点图,还包括了相关性检查,分布图,分箱图,频率图等。用这样的可视化效果图与业务人员沟通,一定会非常愉快的。
但是如果数据维度,不止3个而是30个,数据量也不是几百个点,而是几百万个点,再用2维散点图画出来就会很难看了,而且也表达不清,还会失去重点,计算的复杂度也是非常的高。
当数据量和数据维度多起来,我们就需要用段剖面图来做展示了,放弃个体特征,反应的群体特征和规律。
使用flexclust包中的barchart()函数,画出段剖面图,我们还是用iris数据集进行举例。
> library(flexclust)
> clk2 <- cclust(iris[,-5], k=3);clk2
kcca object of family ‘kmeans’
call:
cclust(x = iris[, -5], k = 3)
cluster sizes:
1 2 3
39 61 50
# 画出段剖面图
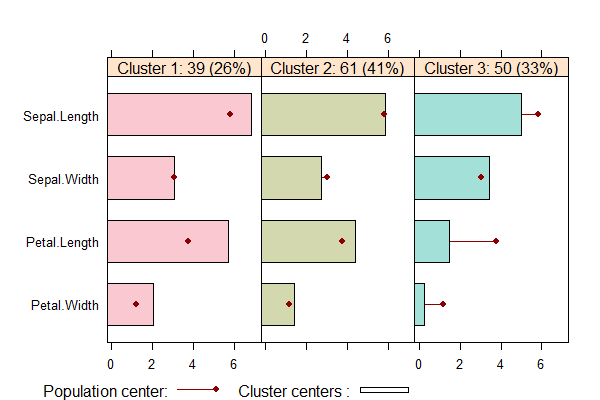
> barchart(clk2,legend=TRUE)
如上图所示,每一区块是一个类别,每行是不同的指标。红点表示均值,柱状是这个类别每个指标的情况,透明色表示不重要指标。
查看段剖面图,可以清楚的看到,每个分组中特征是非常明显的。
- Cluster1中,有39个数据点占26%,Sepal.Width指标在均值附近,其他指标都大于均值。
- Cluster2中,有61个数据点占41%,Sepal.Width指标略小于均值,其他指标在均值附近。
- Cluster3中,有50个数据点占33%,Sepal.Width略大于均值,其他指标都小于均值。
从段剖面图,我们可以一眼就能直观地发现数据聚类后的每个分组的总体特征,而不是每个分组中数据的个体特征,对于数据的解读是非常有帮助的。
对于段剖面图,原来我并不知道是什么效果。在和业务人员沟通中,发现他们使用SAS软件做出了很漂亮的段剖面图,而且他们都能理解,后来我发现R语言也有这个工具函数,图确实能极大地帮助进行数据解读,所以写了这篇文章记录一下。
本文介绍了k-means的聚类计算方法和具体的使用方法,也是对最近做了一个聚类模型的总结。作为数据分析师,我们不仅自己能发现数据的规律,还要让业务人员看明白你的思路,看懂数据的价值,这也是算法本身的价值。
转载请注明出处:
http://blog.fens.me/r-cluster-kmeans