算法为王系列文章,涵盖了计算机算法,数据挖掘(机器学习)算法,统计算法,金融算法等的多种跨学科算法组合。在大数据时代的背景下,算法已经成为了金字塔顶的明星。一个好的算法可以创造一个伟大帝国,就像Google。
算法为王的时代正式到来….
关于作者:
- 张丹, 分析师/程序员/Quant: R,Java,Nodejs
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-graph-shortest-path-bellman-ford/
前言
最短路径是图算法中的基本算法,被普遍应用于多种场景中,如企业生产经营的场景中,现金流的生产和交换的过程,会产生正向的现金流比如经营收入所得,也会产生负向的现金流比如借款、支出等。如果我们以企业作为节点,以现金流做为边时,由于出现了负向的现金流的边,这样构成负权重的网络图谱,就需要用Bellman-Ford算法来实现。
常用的最短路径算法包括:Dijkstra算法,A star算法,Bellman-Ford算法,SPFA算法(Bellman-Ford算法的改进版本),Floyd-Warshall算法,Johnson算法以及Bi-direction BFS算法。
目录
- Bellman-Ford算法介绍
- R语言调用Bellman-Ford算法
- 自己手写Bellman-Ford算法
- 算一个复杂点的网络关系图
1. Bellman-Ford算法介绍
Bellman Ford算法最初于1955年被Alfonso Shimbel提出,但最终基于1958和1956年发表论文的 Richard Bellman和Lester Ford, Jr.二人命名。Edward F. Moore于1957年也提出了该算法,因此该算法有时也称作是Bellman Ford Moore算法。
Bellman-Ford算法与Dijkstra算法一样,解决的是单源最短路径问题。两者不同之处在于,Dijkstra只适用于无负权边的图,而Bellman-Ford算法无此限制:无论是否有向,无论是否有负权边,只要图中没有负权环,则该算法可以正确地给出起点到其余各点的最短路径,否则报告负权环的存在。
Bellman-Ford 算法采用动态规划进行设计,实现的时间复杂度为 O(V*E),其中 V 为顶点数量,E 为边的数量。每次松弛操作实际上是对相邻节点的访问(相当于广度优先搜索),第n次松弛操作保证了所有深度为n的路径最短。由于图的最短路径最长不会经过超过|V| – 1条边,所以可知贝尔曼-福特算法所得为最短路径,也可只时间复杂度为O(VE)。
Bellman-Ford 算法描述:
- 创建源顶点 v 到图中所有顶点的距离的集合 distSet,为图中的所有顶点指定一个距离值,初始均为 Infinite,源顶点距离为 0;
- 计算最短路径,执行 V – 1 次遍历;
- 对于图中的每条边:如果起点 u 的距离 d 加上边的权值 w 小于终点 v 的距离 d,则更新终点 v 的距离值 d;
- 检测图中是否有负权边形成了环,遍历图中的所有边,计算 u 至 v 的距离,如果对于 v 存在更小的距离,则说明存在环;
下面,我们来举例说明一下算法,创建一个带负权重的有向图,来描述对最短路径
开始点为A,数组U为开始列,数组S为上层节点列。通过6次遍历,找到从A到G的最短路径。
通过4次遍历,其实就能获得从A到D的最短路径。
2. R语言调用Bellman-Ford算法
接下来,我们可以继续使用R语言的igraph包来进行实现。新建数据集,如上面例子所示。
# 加载igraph库
> library(igraph)
# 新建图数据
> df<-data.frame(
+ from=c("A","A","B","B","B","D","D","E"),
+ to=c("B","C","C","D","E","B","C","D"),
+ weight=c(-1,4,3,2,2,1,5,-3)
+ )
# 用igraph画图
> a<-graph_from_data_frame(df, directed = TRUE)
> E(a)$arrow.size<-1
> E(a)$arrow.width<-0.2
> E(a)$label<-df$weight
# layout需要设置一下,不然图的展示会很不好看
> plot(a,layout=layout.gem)
layout需要设置一下,不然图的展示会节点叠加在一起,就看不出来图的样子了,我这里选择layout.gem类型。
然后,使用shortest.paths()函数,进行bellman-ford算法计算最短路径的时候,就报错了。错误提示,图形成负权重的环路。
# 使用bellman-ford算法
> shortest.paths(a,"A", algorithm = "bellman-ford")
Error in shortest.paths(a, "A", algorithm = "bellman-ford") :
At core/paths/bellman_ford.c:157 : cannot run Bellman-Ford algorithm, Negative loop detected while calculating shortest paths
尝试了多种数据集,只要是有负值shortest.paths()函数都会报错,无论是否有负权重的环路,我也尝试找了几个的其他的R包,竟然没有发现Bellman-Ford算法的实现,因此只好自己手动写一个了。
3. 自已手写Bellman-Ford算法
于是,我就自己实现bellman-ford算法函数。写了2个小时,好像不练习了,可能还是会有bug吧。
在实现过程中,我们没有做“环”的判断,可能会导致计算逻辑出现问题。我假设了节点的寻路的过程是排序好的,不会出现对于一节点的反复寻路,当然这个假设条件,在某些复杂的场景中是不靠谱的,所以大家在使用的我的代码的时候,当一个基本版参考和学习用,不要直接用于自己的生产环境。
# bellman-ford 最短距离算法
# @param df数据集
# @param start开始节点
bellman_ford<-function(df,start="A"){
# 初始化结果数据集
rs<-data.frame(from=start,to=start,weight=0)
# 初始化结束节点
finishnode<-c()
# 初始化开始节点
nodes<-rs
# 当开始节点数量<结束节点数量时,继续循环计算
while(length(finishnode)<length(rs$to)){
# 过滤已计算过的结束节点
if(length(finishnode)>0){
nodes<-rs[-which(rs$to %in% finishnode),]
}
# 对原始数据进行循环,遍历每一行
for(i in 1:nrow(df)){
row<-df[i,];row
# 对结束节点进行循环,遍历每一个结束节点
for(j in nodes$to){
if(row$from==j){
# 把之前结束节点的权重叠加本次计算中
row$weight<-row$weight+rs$weight[which(rs$to==j)]
# 把结束节点加入到结果数据集
rs<-rbind(rs,row)
}
}
}
# 保留最短的唯一结束节点
rs2<-rs[order(rs$weight),]
n<-which(duplicated(rs2$to))
if(length(n)<0){
rs2<-rs2[-n,]
rs<-rs2[order(as.numeric(row.names(rs2))),]
}
# 更新已经完成的结束节点
finishnode<-c(finishnode,nodes$to)
}
return(rs)
}
执行计算,计算A点其他所有节点的距离。
> rs<-bellman_ford(df,"A")
> rs
from to weight
1 A A 0
2 A B -1
3 B C 2
5 B E 1
8 E D -2
结果数据集中,to 表示从开始点A到节点的距离,每一行from 到 to 表示,最短路径的顺序。
# 计算2点间的最短路径
# @param rs 结果数据集
# @param start 开始节点
# @param end 结束节点
get_shortest_path<-function(rs,start,end){
# 初始化节点
q<-c(start)
idx<-which(rs$from==start)
# 判断有几个分支
if(length(idx)>0){
for(i in idx){
# 递归计算
q2<-get_shortest_path(rs,rs$to[i],end)
if(tail(q2,1)==end){
q<-c(q,q2)
}
}
}
# 查看队列状态
# print(q)
# 当找到结束节点,程序停止
if(tail(q,1)==end){
return(q)
}
return(q)
}
# 计算从开始节点到结束节点的路径
> path<-get_shortest_path(rs[-1,],"A","D")
> path
[1] "A" "B" "E" "D"
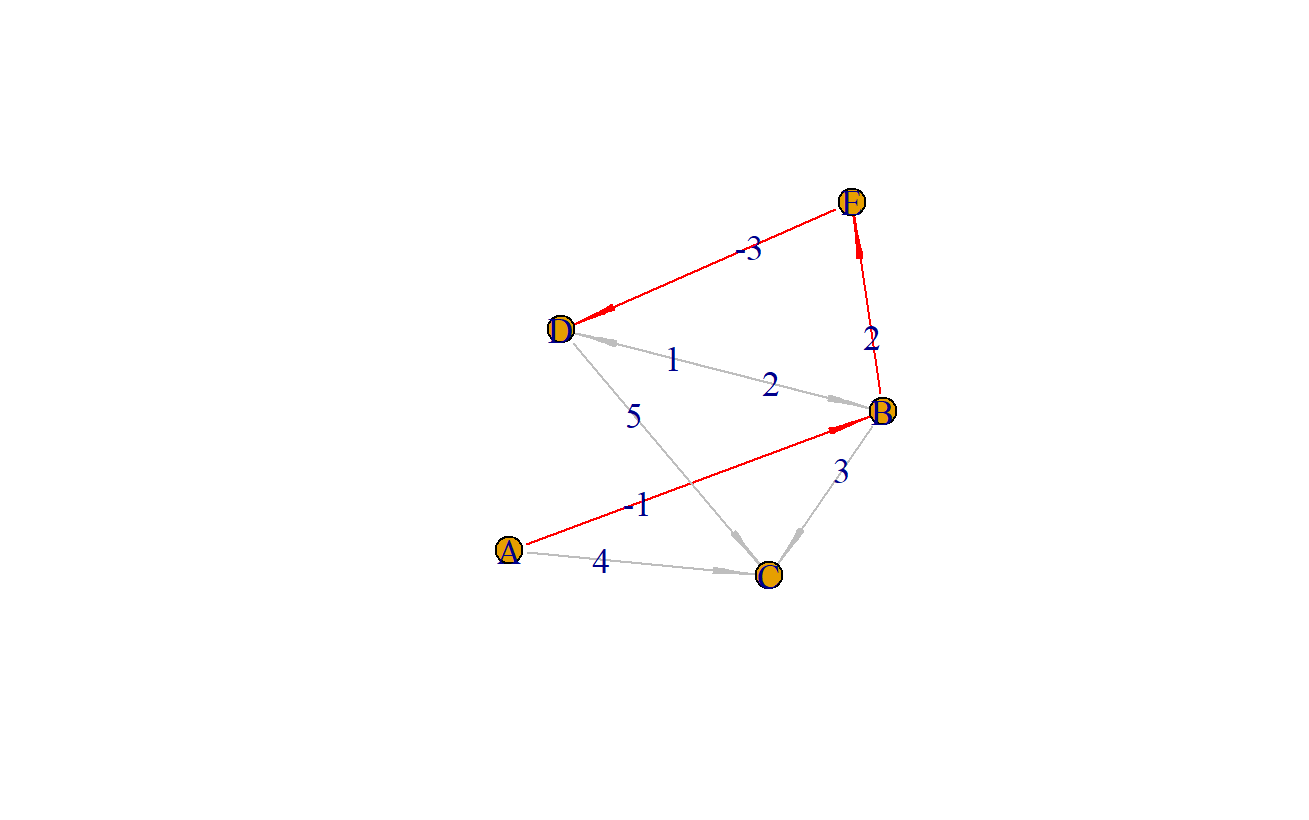
最后,我们把从A点到D的最短路径涂上颜色,来出来。
# 把路径合并成data.frame
> path2<-data.frame(from=path[-length(path)],to=path[-1])
# 找到最短路径的索引
> idx<-which(paste0(df$from,"-",df$to) %in% paste0(path2$from,"-",path2$to))
# 涂色
> df$color<-"gray"
> df$color[idx]<-"red"
> E(a)$color<-df$color
> plot(a,layout=layout.gem)
红色路径就表示从A到D点的最短路径,看上去结果也是对的。在实现过程中,我们没有做“环”的判断,可能会导致计算逻辑出现问题。自己用写了一段算法,用R语言写算法,感觉比起C或者JAVA还要是简单很多的,因为大量基础函数提供了很多的功能和数据结构支持,不用像底层语言什么结构都需要自己从头写起。
4. 算一个复杂点的网路关系图
生成新数据集,共11个节点。
> df2<-data.frame(
+ from=c("A","B","C","D","C","F","B","B","F","G","H","F","E"),
+ to= c("B","C","D","C","E","E","F","G","G","H","I","I","J"),
+ weight=c(5,20,10,-5,75,25,30,60,5,-50,-10,50,100)
+ )
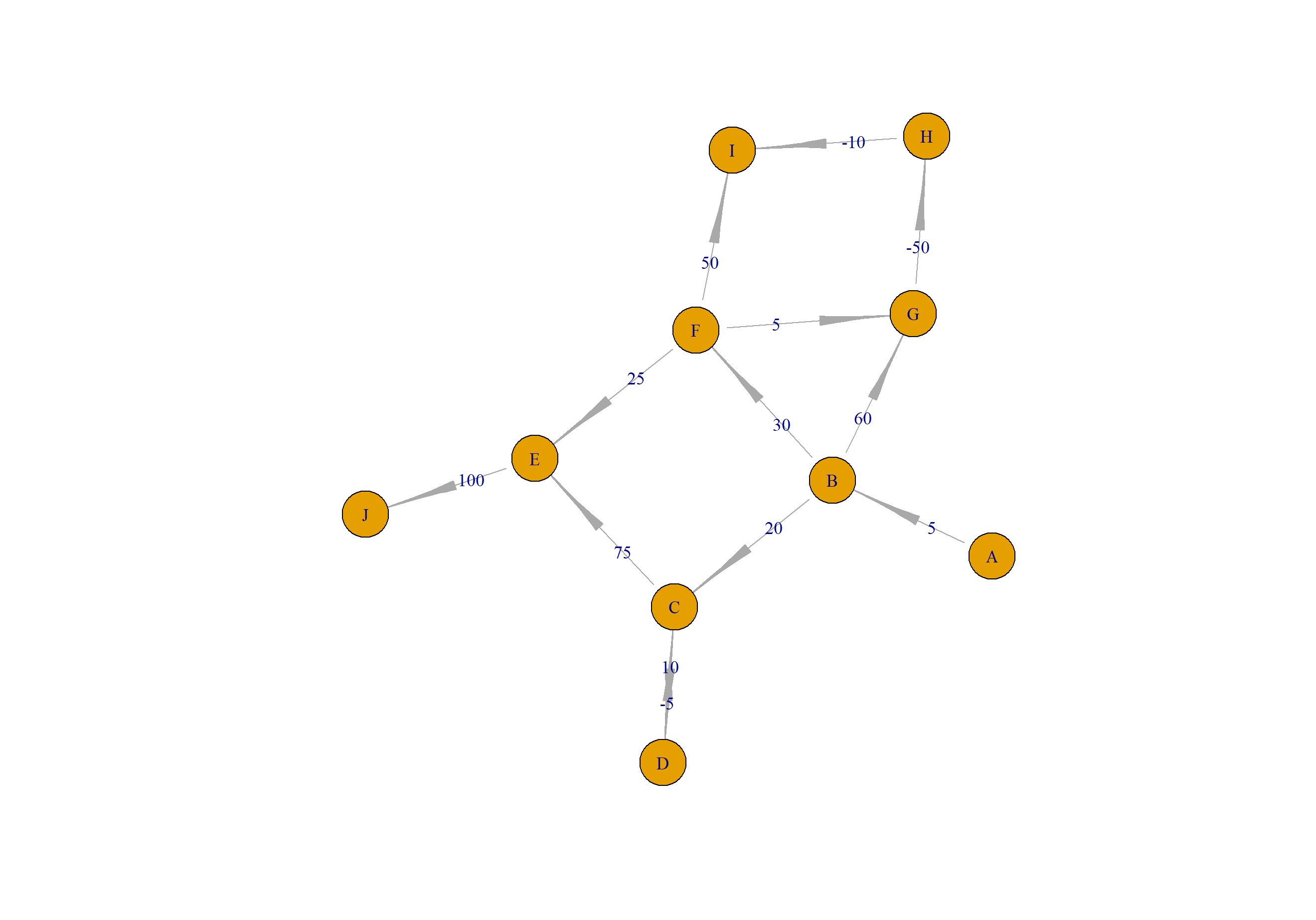
用igraph进行画图展示。
> a2<-graph_from_data_frame(df2, directed = TRUE)
> E(a2)$arrow.size<-1
> E(a2)$arrow.width<-0.2
> E(a2)$label<-df2$weight
> plot(a2,layout=layout.gem)
计算A开始到所有节点的最短路径。
> rs<-bellman_ford(df2,"A")
> rs
from to weight
1 A A 0
2 A B 5
3 C D 35
6 F E 60
7 B F 35
9 F G 40
10 G H -10
11 H I -20
13 E J 160
21 B C 25
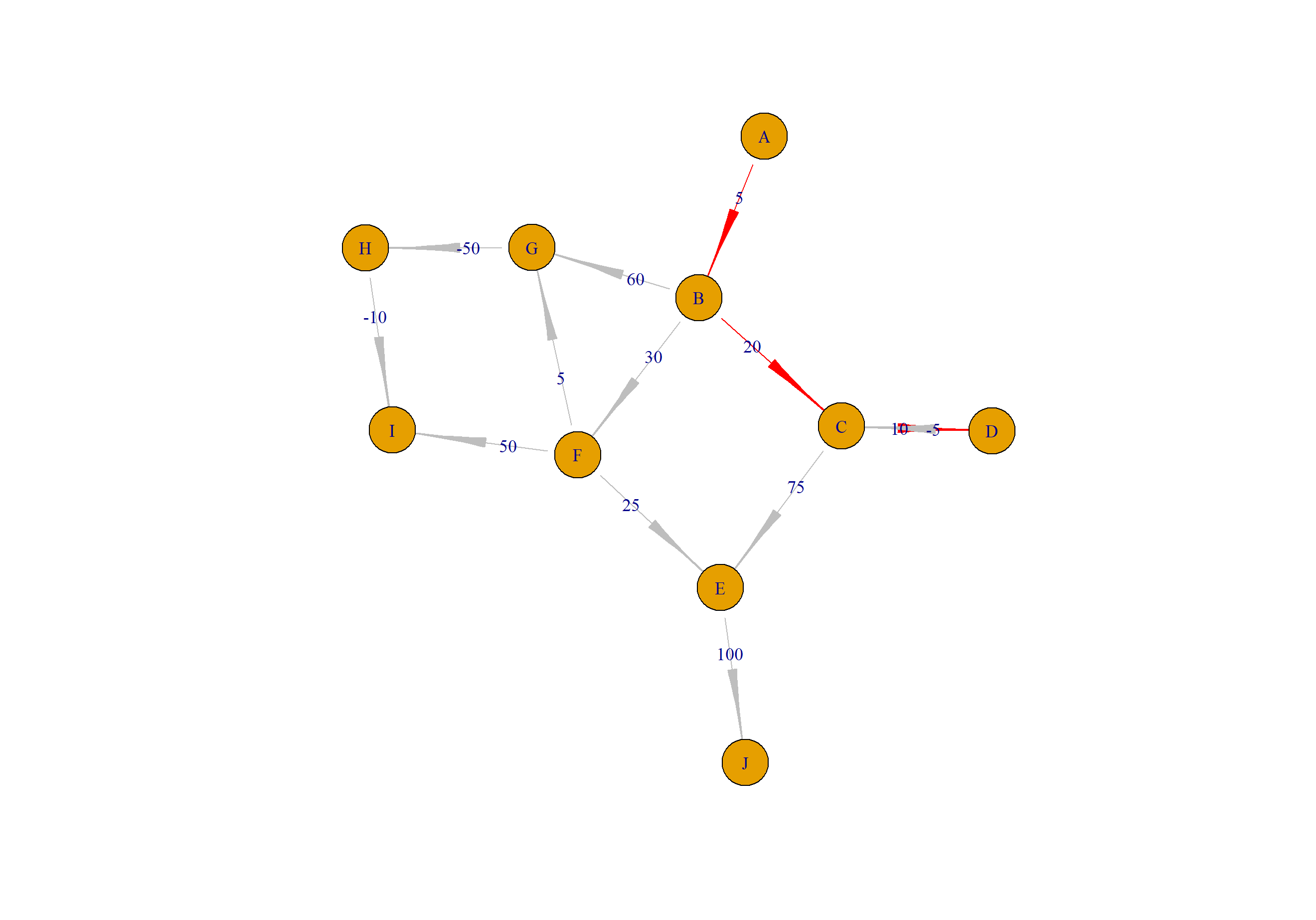
计算A到D的最短路径路线,并画科展示。
# 计算 A 到 D的最短路径
> path<-get_shortest_path(rs[-1,],"A","D")
> path
[1] "A" "B" "C" "D"
# 画图
> path2<-data.frame(from=path[-length(path)],to=path[-1])
> idx<-which(paste0(df2$from,"-",df2$to) %in% paste0(path2$from,"-",path2$to))
> df2$color<-"gray"
> df2$color[idx]<-"red"
> E(a2)$arrow.size<-1
> E(a2)$arrow.width<-0.2
> E(a2)$color<-df2$color
> plot(a2,layout=layout.gem)
计算A到I的最短路径路线,并画科展示。
# 计算 A 到 I的最短路径
> path<-get_shortest_path(rs[-1,],"A","I")
> path
[1] "A" "B" "F" "G" "H" "I"
# 画图
> path2<-data.frame(from=path[-length(path)],to=path[-1])
> idx<-which(paste0(df2$from,"-",df2$to) %in% paste0(path2$from,"-",path2$to))
> df2$color<-"gray"
> df2$color[idx]<-"red"
> E(a2)$arrow.size<-1
> E(a2)$arrow.width<-0.2
> E(a2)$color<-df2$color
> plot(a2,layout=layout.gem)
算法和数据结构还是很重要的,图论算法原来仅在计算领域有应用,随着知识图谱的应用普及,相信未来会有更广阔的应用前景,把原来藏在背后的知识,扩展到前台形成新的模型思路。
努力吧,曾经的少年。
本文算法代码已上传到github: https://github.com/bsspirit/graph/blob/main/Bellman-Ford.r
转载请注明出处:
http://blog.fens.me/r-graph-shortest-path-bellman-ford/






[…] 常用的最短路径算法包括:Dijkstra算法,A star算法,Bellman-Ford算法,SPFA算法(Bellman-Ford算法的改进版本),Floyd-Warshall算法,Johnson算法以及Bi-direction BFS算法。 […]