R的极客理想系列文章,涵盖了R的思想,使用,工具,创新等的一系列要点,以我个人的学习和体验去诠释R的强大。
R语言作为统计学一门语言,一直在小众领域闪耀着光芒。直到大数据的爆发,R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入,R语言的社区在迅速扩大成长。现在已不仅仅是统计领域,教育,银行,电商,互联网….都在使用R语言。
要成为有理想的极客,我们不能停留在语法上,要掌握牢固的数学,概率,统计知识,同时还要有创新精神,把R语言发挥到各个领域。让我们一起动起来吧,开始R的极客理想。
关于作者:
- 张丹,分析师/程序员/Quant: R,Java,Nodejs
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-levenshtein-distance/
前言
文字模糊匹配,是在文字处理时,要常用到的一种功能。比如英文,差一个字母,字母的顺序写反了。要实现对文字的模糊匹配,就可以用到莱文斯坦距离的思路,将一个字符串变为另一个字符串需要进行编辑操作最少的次数。
输入法的拼写检查,纠正用户输入的拼写错误,就是使用到了莱文斯坦距离。
目录
- 莱文斯坦距离介绍
- 算法原理
- R语言代码实现
- adist()函数调用
1. 莱文斯坦距离介绍 Levenshtein Distance
Levenshtein Distance莱文斯坦距离,属于编辑距离的一种,主要用于衡量两个字符串之间的差异。由苏联数学家Vladimir Levenshtein于1965年提出,被广泛应用于拼写纠错检查、DNA分析、语音识别等领域。
两个字符串之间的Levenshtein Distance莱文斯坦距离指的是,将一个字符串变为另一个字符串需要进行编辑操作最少的次数。其中,允许的编辑操作有以下三种,替换、插入、删除。
- 「替换」:将一个字符替换成另一个字符
- 「插入」:插入一个字符
- 「删除」:删除一个字符
例如,计算 house 到 rose 的莱文斯坦距离。
第一步:house 把第一位 h 替换为 r,得到rouse。
第二步:rouse 把第三位 u 删除,得到rose
即完成了计算,莱文斯坦距离为2.
2. 算法原理
对于两个字符串A、B而言,字符串A的前i个字符和字符串B的前j个字符的莱文斯坦距离符合如下公式。
在数学上,两个字符串a,b的莱文斯坦距离:
计算公式:
表示内容:
2.1 第一种情况:当至少存在一个字符串为空串
若字符串A是一个长度为0的空字符串时,则其变为长度为n的字符串B。只需对字符串A进行n次插入操作即可。
例如:
A="",B="abc"时
lev距离 = max(length(A),length(B)) = max(0,3) = 3
同理,若字符串A是一个长度为n的字符串时,则其变为长度为0的空字符串B。则只需对字符串A进行n次删除操作即可。
例如:
A="abcd",B=""时
lev距离 = max(length(A),length(B)) = max(4,0) = 4
故在上述公式中,可将这两种情况统一为: 当两个字符串的长度最小值为0时,则说明有一个字符串为空串。则这二者之间的莱文斯坦距离为两个字符串长度的最大值。
2.2 第二种情况:两个字符串均不为空串
当两个字符串均不为空串时,这里假设字符串A为horse、字符串B为ros。由于替换/插入/删除,三种操作不会改变字符串中各字符的相对顺序。因此,可以每次仅对字符串A进行操作,即只考虑
字符串A的前i个字符 和 字符串B的前j个字符 的莱文斯坦距离,让i和j都从1开始计数。字符串A的前5个字符 和 字符串B的前3个字符 的莱文斯坦距离lev(5,3),就是最终我们所求的字符串A、字符串B之间的莱文斯坦距离3。
【插入】假设我们把 horse 变为 ro 的莱文斯坦距离记为u,即:
# 字符串A的前5个字符 和 字符串B的前3个字符 的莱文斯坦距离为 u
lev(5,2) = u
则 horse 期望变为 ros,其所需的编辑次数不会超过 u+1。因为 horse 只需先经过u次编辑操作变为 ro,然后在尾部插入s字符即可变为 ros
【删除】假设我们把 hors 变为 ros 的莱文斯坦距离记为v,即:
# 字符串A的前4个字符 和 字符串B的前3个字符 的莱文斯坦距离为 v
lev(4,3) = v
则 horse 期望变为 ros,其所需的编辑次数不会超过 v+1。因为 horse 只需先进行一次删除操作变为 hors,再经过v次编辑操作即可变为 ros
【替换】假设我们把 hors 变为 ro 的莱文斯坦距离记为w,即
# 字符串A的前4个字符 和 字符串B的前2个字符 的莱文斯坦距离为 w
lev(4,2) = w
则 horse 期望变为 ros,其所需的编辑次数不会超过 w+1。因为 horse 只经过w次编辑操作即可变为 roe,然后通过一次替换操作,将尾部的e字符替换为s字符即可。
得出莱文斯坦距离满足如下的递推公式
lev(horse, ros) = lev(5,3)
= min( lev(5,2)+1, lev(4,3)+1, lev(4,2)+1 )
= min(u+1, v+1, w+1)
如果 某字符串A的第i个字符 与 某字符串B的第j个字符 完全相同,则其所需的编辑次数肯定不会超过 lev(i-1, j-1)。因为无需进行替换,可跳过该步骤。
通过上面的分析过程,我们其实不难看出。如果期望 字符串A的前i个字符 与 字符串B的前j个字符 完全相同。可以有如下三种途径操作方式进行实现。而最终的莱文斯坦距离就是下面三种实现方式中次数最小的一个。
- 在 字符串A的前i个字符 与 字符串B的前j-1个字符 完全相同的基础上,进行一次「插入」操作
- 在 字符串A的前i-1个字符 与 字符串B的前j个字符 完全相同的基础上,进行一次「删除」操作
- 在 字符串A的前i-1个字符 与 字符串B的前j-1个字符 完全相同的基础上,如果字符串A的第i个字符与字符串B的第j个字符不同,则需要进行一次「替换」操作;如果字符串A的第i个字符与字符串B的第j个字符相同,则无需进行任何操作。
参考文章:https://zhuanlan.zhihu.com/p/507830576
3. R语言代码实现
构建lev_dist()函数,实现莱文斯坦距离,使用递归方法进行实现。想了一种简单的实现方法,但效率太低,看看就好,千万不要用到实际的算法中。等有时间,我再换个思路实现一下。
#######################################
# Levenshtein 莱文斯坦距离,递归实现(效率很低)
######################################
> lev_dist<-function(txt1,txt2){
+ len1<-nchar(txt1)
+ len2<-nchar(txt2)
+
+ if(len1==0) return(len2)
+ if(len2==0) return(len1)
+
+ # 插入消耗
+ insert_cost <- lev_dist(txt1, substring(txt2,1,len2-1)) + 1;
+
+ # 删除消耗
+ delete_cost <- lev_dist(substring(txt1,1,len1-1), txt2) + 1;
+
+ # 替换消耗
+ cost<-ifelse(substring(txt1,len1,len1) == substring(txt2,len2,len2),0,1)
+ replaces_cost <- lev_dist(substring(txt1,1,len1-1), substring(txt2,1,len2-1)) + cost;
+
+ rs<-min(insert_cost,delete_cost,replaces_cost)
+ print(paste("txt1:",txt1,"txt2:",txt2,"insert:",insert_cost,"delete:",delete_cost,"replaces:",replaces_cost))
+ return(rs)
+ }
对结果进行测试
# 测试ab和a的情况
> lev_dist("ab","a")
[1] "txt1: a txt2: a insert: 2 delete: 2 replaces: 0"
[1] "txt1: ab txt2: a insert: 3 delete: 1 replaces: 2"
[1] 1
# 测试ab和abc的情况
> lev_dist("ab","abc")
[1] "txt1: a txt2: a insert: 2 delete: 2 replaces: 0"
[1] "txt1: ab txt2: a insert: 3 delete: 1 replaces: 2"
[1] "txt1: a txt2: a insert: 2 delete: 2 replaces: 0"
[1] "txt1: a txt2: ab insert: 1 delete: 3 replaces: 2"
[1] "txt1: a txt2: a insert: 2 delete: 2 replaces: 0"
[1] "txt1: ab txt2: ab insert: 2 delete: 2 replaces: 0"
[1] "txt1: a txt2: a insert: 2 delete: 2 replaces: 0"
[1] "txt1: a txt2: ab insert: 1 delete: 3 replaces: 2"
[1] "txt1: a txt2: abc insert: 2 delete: 4 replaces: 3"
[1] "txt1: a txt2: a insert: 2 delete: 2 replaces: 0"
[1] "txt1: a txt2: ab insert: 1 delete: 3 replaces: 2"
[1] "txt1: ab txt2: abc insert: 1 delete: 3 replaces: 2"
[1] 1
让单词变长,虽然莱文斯坦距离并不大,但是计算次数是相当的多,效率非常低。
> lev_dist("kitten","sitting")
....
....
// 省略
3
用递归的方式,虽然比较容易实现,但是效率太低,没有办法是应用中使用。
4. adist()函数
在R的基础包utils中,找到了 adist()函数,就实现了莱文斯坦距离,我们可以直接使用adist()来完成,莱文斯坦距离的计算。还是R语言原生的程序效率高!!
分别测试 house 到 rose,horse 到 ros的 莱文斯坦距离。
#
> adist("house","rose")
[,1]
[1,] 2
> adist("horse","ros")
[,1]
[1,] 3
查看替换sub 、插入ins 、删除del ,分别使用了几次。
> drop(attr(adist("horse", "rose", counts = TRUE), "counts"))
ins del sub
0 1 1
按顺序查看替换、插入、删除的操作步骤,S=替换,M为跳过,D为删除,I为插入
> attr(adist("horse", "rosxeee", counts = TRUE), "trafos")
[,1]
[1,] "SMDMIIIM"
本文我们了解了莱文斯坦距离的原理和实现,后面我们就可以利用莱文斯坦距离的特性,对文字进行相似度的距离计算,从而实现文本的模糊匹配。本文代码:https://github.com/bsspirit/r-string-match/blob/main/levenshtein.r
转载请注明出处:
http://blog.fens.me/r-levenshtein-distance/


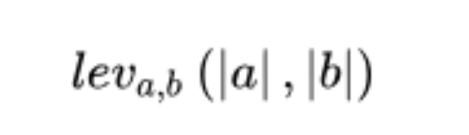
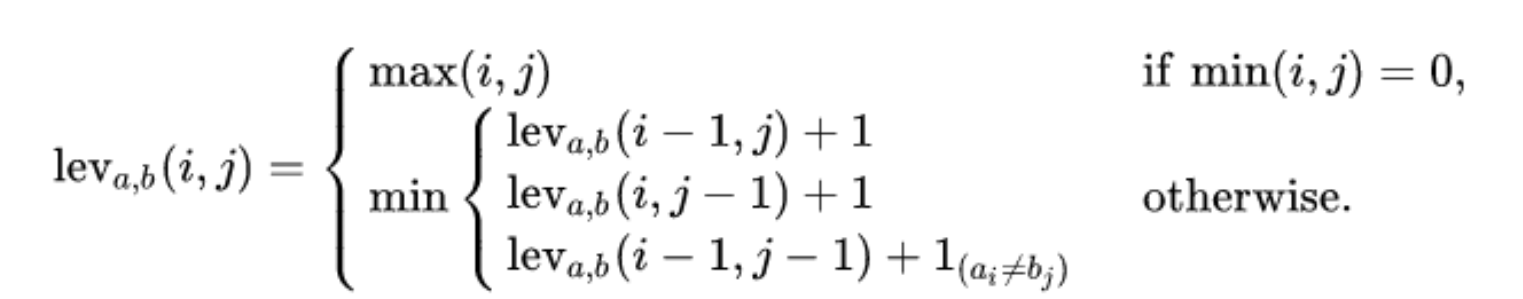

[…] Hamming Distance汉明距离,是以理查德·卫斯里·汉明的名字命名的。在信息论中,两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。换句话说,它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。汉明距离的计算思路与莱文斯坦距离算法有类似之处,参考文章R语言莱文斯坦距离算法Levenshtein Distance […]