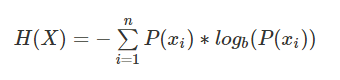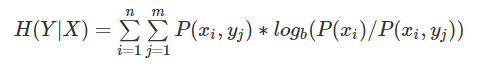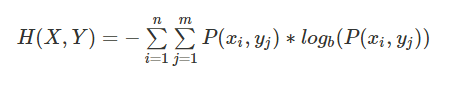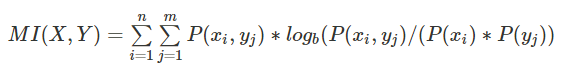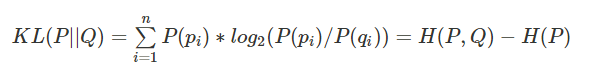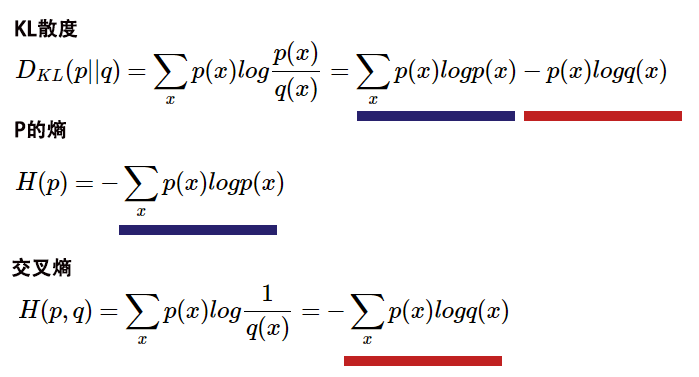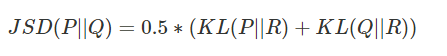R的极客理想系列文章,涵盖了R的思想,使用,工具,创新等的一系列要点,以我个人的学习和体验去诠释R的强大。
R语言作为统计学一门语言,一直在小众领域闪耀着光芒。直到大数据的爆发,R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入,R语言的社区在迅速扩大成长。现在已不仅仅是统计领域,教育,银行,电商,互联网….都在使用R语言。
要成为有理想的极客,我们不能停留在语法上,要掌握牢固的数学,概率,统计知识,同时还要有创新精神,把R语言发挥到各个领域。让我们一起动起来吧,开始R的极客理想。
关于作者:
- 张丹(Conan), 程序员/Quant: Java,R,Nodejs
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-entropy
前言
香农的《通信的数学理论》是20世纪非常伟大的著作,被认为是现代信息论研究的开端。信息论定义了信息熵,用于把信息进行度量,以比特(bit)作为量纲单位,为如今发达的信息产业和互联网产业奠定了基础。本文接上一篇文章R语言实现46种距离算法,继续philentropy包的介绍,包括信息度量函数的使用。
目录
- 信息熵介绍
- 关键概念
- 信息度量函数
- 应用举例
1.信息熵介绍
信息论(Information Theory)是概率论与数理统计的一个分枝,用于研究信息处理、信息熵、通信系统、数据传输、率失真理论、密码学、信噪比、数据压缩等问题的应用数学学科。信息论将信息的传递作为一种统计现象来考虑,给出了估算通信信道容量的方法。信息传输和信息压缩是信息论研究中的两大领域。
香农被称为是“信息论之父”,香农于1948年10月发表的A Mathematical Theory of Communication,通信的数学理论(中文版),通常被认为是现代信息论研究的开端。
信息熵,是对信息随机性的量度,又指信息能被压缩的极限,用bit作为衡量信息的最小单位。一切信息所包含的信息量,都是1bit的正整数倍。计算机系统中常采用二进制编码,一个0或1就是1bit。
举例来说明一下信息熵的计算原理,假设小明最喜欢5种水果,苹果、香蕉、西瓜、草莓、樱桃中的一种,如果小明没有偏爱,选择每种水果的概率都是20%,那么这一信息的信息熵为
H(A) = -1*(0.2*log2(0.2)*5)
= 2.321928 bits如果小明偏爱香蕉,选择这5种水果的概率分别是10%,20%,45%,15%,10%,那么这一信息信息熵为
H(B)=-1*(0.1*log2(0.1)+0.2*log2(0.2)+0.45*log2(0.45)+0.15*log2(0.15)+0.1*log2(0.1))
= 2.057717 bits
从结果得到H(A)大于H(B),信息熵越大表示越不确定。对于B的情况,对某一种水果的偏好,比A增加了确定性的因素,所以H(B)小于H(A)是符合对于信息熵的定义的。
2. 关键概念
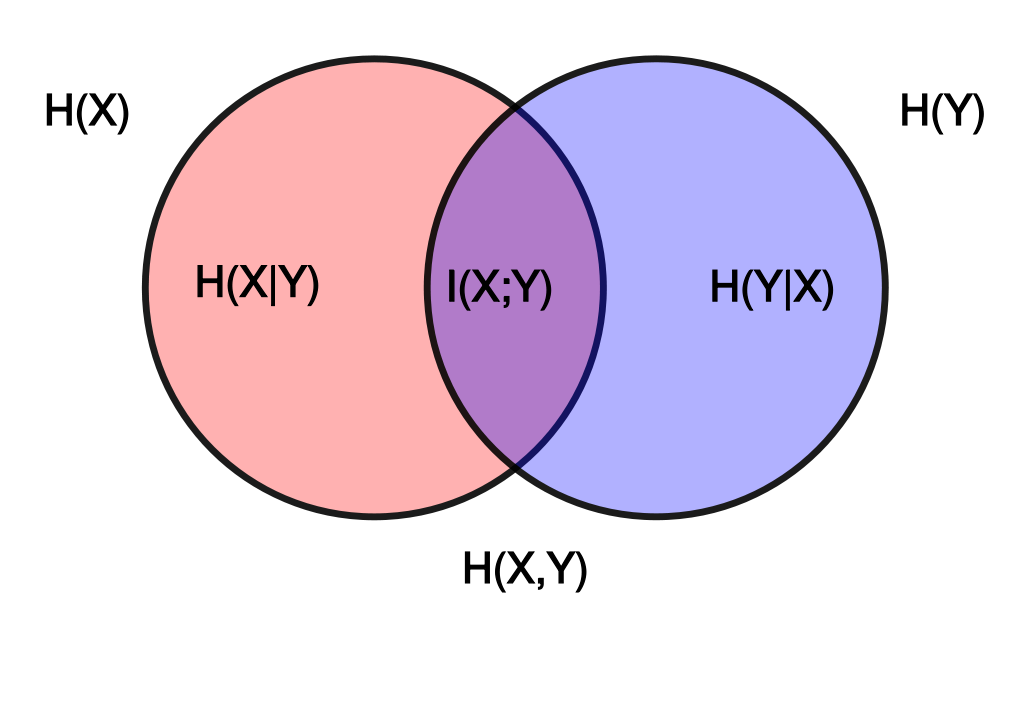
我们从一幅图来认识信息熵,图中显示了随机变量X和Y的2个集合,在信息熵的概念里的所有可能逻辑关系。两个圆所包含的面积为联合熵H(X,Y), 左边的整个圆表示X的熵H(X),左边半圆是条件熵H(X|Y)。 右边的整个圆表示Y的熵H(Y),右边半圆条件熵H(Y|X),中间交集的部分是互信息I(X; Y)。
信息熵(Entropy):是对信息随机性的量度,用于计算信息能被压缩的极限。对随机变量X,不确定性越大,X的信息熵H(X)也就越大。
公式定义:
H(x)的取值范围,0<=H(x)<=log(n), 其中n是随机变量x取值的种类数。需要注意的是,熵只依赖于随机变量的分布,与随机变量取值无关。
条件熵(Conditional Entropy):表示两个随机变量X和Y,在已知Y的情况下对随机变量X的不确定性,称之为条件熵H(X|Y),
公式定义:
联合熵(Joint Entropy):表示为两个随机事件X和Y的熵的并集,联合熵解决将一维随机变量分布推广到多维随机变量分布。
公式定义:
互信息(Mutual Information, 信息增益):两个随机变量X和Y,Y对X的互信息,为后验概率与先验概率比值的对数,即原始的熵H(X)和已知Y的情况下的条件熵H(X|Y)的比值的对数,信息增益越大表示条件Y对于确定性的贡献越大。互信息,也可以用来衡量相似性。
公式定义:
当MI(X,Y)=0时,表示两个事件X和Y完全不相关。决策树ID3算法就是使用信息增益来划分特征,信息增益大时,说明对数据划分帮助很大,优先选择该特征进行决策树的划分。
信息增益比率:是信息增益与该特征的信息熵之比,用于解决信息增益对多维度特征的选择,决策树C4.5算法使用信息增益比率进行特征划分。
KL散度(Kullback–Leibler Divergence, 相对熵):随机变量x取值的两个概率分布p和q,用来衡量这2个分布的差异,通常用p表示真实分布,用q表示预测分布。
公式定义:
n为事件的所有可能性,如果两个分布完全相同,那么它们的相关熵为0。如果相对熵KL越大,说明它们之间的差异越大,反之相对熵KL越小,说明它们之间的差异越小。
交叉熵(Cross Entropy):是对KL散度的一种变型,把KL散度log(p(x)/q(x))进行拆分,前面部分就是p的熵H(p),后面就是交叉熵H(p,q)。
公式定义:
交叉熵可以用来计算学习模型分布与训练分布之间的差异,一般在机器学习中直接用交叉熵做损失函数,用于评估模型。
信息论是通信理论的基础,也是xx的基础,关于信息论的理论,等后面有时时间再做分享,本文重要研究信息熵的函数计算问题。
3. 信息度量函数
philentropy包的函数,主要分为3种类别的函数,第一类是距离测量的函数,第二类是相关性分析,第三类是信息度量函数,本文重点介绍这些信息度量的函数。有关于距离测量函数和相关性分析函数,请参考文章R语言实现46种距离算法
我们来看一下,philentropy包里信息度量的函数:
- H(): 香农熵, Shannon’s Entropy H(X)
- JE() : 联合熵, Joint-Entropy H(X,Y)
- CE() : 条件熵, Conditional-Entropy H(X|Y)
- MI() : 互信息, Shannon’s Mutual Information I(X,Y)
- KL() : KL散度, Kullback–Leibler Divergence
- JSD() : JS散度,Jensen-Shannon Divergence
- gJSD() : 通用JS散度,Generalized Jensen-Shannon Divergence
本文的系统环境为:
- Win10 64bit
- R: 3.4.2 x86_64-w64-mingw32
3.1 H()香农熵
H()函数,可用于快速计算任何给定概率向量的香农熵。
H()函数定义:
H (x, unit = "log2")
参数列表:
- x, 概率向量
- unit,对数化的单位,默认为log2
函数使用:
# 创建数据x
> x<-1:10;x
[1] 1 2 3 4 5 6 7 8 9 10
> px<-x/sum(x);x1
[1] 0.01818182 0.03636364 0.05454545 0.07272727
[5] 0.09090909 0.10909091 0.12727273 0.14545455
[9] 0.16363636 0.18181818
# 计算香农熵
> H(px)
[1] 3.103643
同样地,我们也可以用程序实现公式自己算一下。
# 创建数据x
> x<-1:10
#计算x的概率密度px
> px<-x/sum(x)
# 根据公式计算香农熵
> -1*sum(px*log2(px))
[1] 3.103643
我们动手的计算结果,用于H()函数的计算结果是一致的。
3.2 CE()条件熵
CE()函数,基于给定的联合概率向量P(X,Y)和概率向量P(Y),根据公式 H(X|Y)= H(X,Y)-H(Y)计算香农的条件熵。
函数定义:
CE(xy, y, unit = "log2")参数列表:
- xy, 联合概率向量
- y, 概率向量,必须是随机变量y的概率分布
- unit,对数化的单位,默认为log2
函数使用:
> x3<- 1:10/sum(1:10)
> y3<- 30:40/sum(30:40)
# 计算条件熵
> CE(x3, y3)
[1] -0.3498852
3.3 JE()联合熵
JE()函数,基于给定的联合概率向量P(X,Y)计算香农的联合熵H(X,Y)。
JE()函数定义:
JE (x, unit = "log2")
参数列表:
- x, 联合概率向量
- unit,对数化的单位,默认为log2
函数使用:
# 创建数据x
> x2 <- 1:100/sum(1:100)
# 联合熵
> JE(x2)
[1] 6.372236
3.4 MI()互信息
MI()函数,根据给定联合概率向量P(X,Y)、概率向量P(X)和概率向量P(X),按公式I(X,Y)= H(X)+ H(Y)-H(X,Y)计算。
函数定义:
MI(x, y, xy, unit = "log2")参数列表:
- x, 概率向量
- x, 概率向量
- xy, 联合概率向量
- unit,对数化的单位,默认为log2
函数使用:
# 创建数据集
> x3 <- 1:10/sum(1:10)
> y3<- 20:29/sum(20:29)
> xy3 <- 1:10/sum(1:10)
# 计算互信息
> MI(x3, y3, xy3)
[1] 3.311973
3.5 KL()散度
KL()函数,计算两个概率分布P和Q的Kullback-Leibler散度。
函数定义:
KL(x, test.na = TRUE, unit = "log2", est.prob = NULL)参数列表:
- x, 概率向量或数据框
- test.na, 是否检查NA值
- unit,对数化的单位,默认为log2
- est.prob, 用计数向量估计概率的方法,默认值NULL。
函数使用:
# 创建数据集
> df4 <- rbind(x3,y3);df4
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9]
x3 0.01818182 0.03636364 0.05454545 0.07272727 0.09090909 0.1090909 0.1272727 0.1454545 0.1636364
y3 0.08163265 0.08571429 0.08979592 0.09387755 0.09795918 0.1020408 0.1061224 0.1102041 0.1142857
[,10]
x3 0.1818182
y3 0.1183673
# 计算KL散度
> KL(df4, unit = "log2") # Default
kullback-leibler
0.1392629
> KL(df4, unit = "log10")
kullback-leibler
0.0419223
> KL(df4, unit = "log")
kullback-leibler
0.09652967
3.5 JSD()散度
JSD()函数,基于具有相等权重的Jensen-Shannon散度,计算距离矩阵或距离值。
公式定义:
函数定义:
JSD(x, test.na = TRUE, unit = "log2", est.prob = NULL)参数列表:
- x, 概率向量或数据框
- test.na, 是否检查NA值
- unit, 对数化的单位,默认为log2
- est.prob, 用计数向量估计概率的方法,默认值NULL。
# 创建数据
> x5 <- 1:10
> y5 <- 20:29
> df5 <- rbind(x5,y5)
# 计算JSD
> JSD(df5,unit='log2')
jensen-shannon
50.11323
> JSD(df5,unit='log')
jensen-shannon
34.73585
> JSD(df5,unit='log10')
jensen-shannon
15.08559
# 计算JSD,满足est.prob
> JSD(df5, est.prob = "empirical")
jensen-shannon
0.03792749
3.6 gJSD()散度
gJSD()函数,计算概率矩阵的广义Jensen-Shannon散度。
公式定义:
函数定义:
gJSD(x, unit = "log2", weights = NULL)参数列表:
- x, 概率矩阵
- unit, 对数化的单位,默认为log2
- weights, 指定x中每个值的权重,默认值NULL。
# 创建数据
> Prob <- rbind(1:10/sum(1:10), 20:29/sum(20:29), 30:39/sum(30:39))
# 计算gJSD
> gJSD(Prob)
[1] 0.023325
4. 应用举例
在我们了解了熵的公式原理和使用方法后,我们就可以做一个案例来试一下。我们定义一个场景的目标:通过用户的看书行为,预测用户是否爱玩游戏。通过我们一步一步地推倒,我们计算出熵,条件熵,联合熵,互信息等指标。
第一步,创建数据集为2列,X列用户看书的类型,包括旅游(Tourism)、美食(Food)、IT技术(IT),Y列用户是否喜欢打游戏,喜欢(Y),不喜欢(N)。
X,Y
Tourism,Y
Food,N
IT,Y
Tourism,N
Tourism,N
IT,Y
Food,N
Tourism,Y
第二步,建立联合概率矩阵,分别计算H(X),Y(X)。
| X | Y | N | p(X) |
| Tourism | 2/8=0.25 | 2/8=0.25 | 0.25+0.25=0.5 |
| Food | 0/8=0 | 2/8=0.25 | 0+0.25=0.25 |
| IT | 2/8=0.25 | 0/8=0 | 0.25+0=0.25 |
| p(Y) | 0.25+0+0.25=0.5 | 0.25+0.25+0=0.5 |
计算过程
# 分别计算每种情况的概率
p(X=Tourism) = 2/8 + 2/8 = 0.5
p(X=Food) = 2/8 + 0/8 = 0.25
p(X=IT) = 0/8 + 2/8 = 0.25
p(Y=Y) = 4/8 = 0.5
p(Y=N) = 4/8 = 0.5
# 计算H(X)
H(X) = -∑p(xi)*log2(p(xi))
= -p(X=Tourism)*log2(p(X=Tourism) ) -p(X=Food)*log2(p(X=Food) ) -p(X=IT)*log2(p(X=IT) )
= -0.5*log(0.5) -0.25*log(0.25) - 0.25*log(0.25)
= 1.5
# 计算H(Y)
H(Y) = -∑p(yi)*log2(p(yi))
= -p(Y=Y)*log2(p(Y=Y)) -p(Y=N)*log2(p(Y=N))
= -0.5*log(0.5) -0.5*log(0.5)
= 1
第三步,计算每一项的条件熵,H(Y|X=Tourism),H(Y|X=Food),H(Y|X=IT)。
H(Y|X=Tourism) = -p(Y|X=Tourism)*log(p(Y|X=Tourism)) - p(N|X=Tourism)*log(p(N|X=Tourism))
= -0.5*log(0.5) -0.5*log(0.5)
= 1
H(Y|X=Food) = -p(Y|X=Food)*log(p(Y|X=Food)) -p(N|X=Food)*log(p(N|X=Food))
= -0*log(0) -1*log(1)
= 0
H(Y|X=IT) = -p(Y|X=IT)*log(p(Y|X=IT)) -p(N|X=IT)*log(p(N|X=IT))
= -1*log(1) -0*log(0)
= 0
第四步,计算条件熵H(Y|X)
H(Y|X) = ∑p(xi)*H(Y|xi)
= p(X=Tourism)*H(Y|X=Tourism) + p(X=Food)*H(Y|X=Food) + p(X=IT)*H(Y|X=IT)
= 0.5*1 + 0.25*0 + 0.25*0
= 0.5
第五步,计算联合熵H(X,Y)
H(X,Y) = −∑p(x,y)log(p(x,y))
= H(X) + H(Y|X)
= 1.5 + 0.5
= 2
第六步,计算互信息I(X;Y)
I(X;Y) = H(Y) - H(Y|X) = 1 - 0.5 = 0.5
= H(X) + H(Y) - H(X,Y) = 1.5 + 1 - 2 = 0.5
我们把上面的推到过程,用程序来实现一下。
# 创建数据集
> X<-c('Tourism','Food','IT','Tourism','Tourism','IT','Food','Tourism')
> Y<-c('Y','N','Y','N','N','Y','N','Y')
> df<-cbind(X,Y);df
X Y
[1,] "Tourism" "Y"
[2,] "Food" "N"
[3,] "IT" "Y"
[4,] "Tourism" "N"
[5,] "Tourism" "N"
[6,] "IT" "Y"
[7,] "Food" "N"
[8,] "Tourism" "Y
变型为频率矩阵
> tf<-table(df[,1],df[,2]);tf
N Y
Food 2 0
IT 0 2
Tourism 2 2
计算概率矩阵
> pX<-margin.table(tf,1)/margin.table(tf);pX
Tourism Food IT
0.50 0.25 0.25
> pY<-margin.table(tf,2)/margin.table(tf);pY
Y N
0.5 0.5
> pXY<-prop.table(tf);pXY
Y N
Tourism 0.25 0.25
Food 0.00 0.25
IT 0.25 0.00
计算熵
> H(pX)
[1] 1.5
> H(pY)
[1] 1
# 条件熵
> CE(pX,pY)
[1] 0.5
# 联合熵
> JE(pXY)
[1] 2
# 互信息
> MI(pX,pY,pXY)
[1] 0.5
计算原理是复杂的,用R语言的程序实现却是很简单的,几行代码就搞定了,
本文只是对的信息论的初探,重点还是在信息度量方法的R语言实现。信息熵作为信息度量的基本方法,对各种主流的机器学习的算法都有支撑,是我们必须要掌握的知识。了解本质才能发挥数据科学的潜力,学习的路上不断积累和前进。
转载请注明出处:
http://blog.fens.me/r-entropy