R的极客理想系列文章,涵盖了R的思想,使用,工具,创新等的一系列要点,以我个人的学习和体验去诠释R的强大。
R语言作为统计学一门语言,一直在小众领域闪耀着光芒。直到大数据的爆发,R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入,R语言的社区在迅速扩大成长。现在已不仅仅是统计领域,教育,银行,电商,互联网….都在使用R语言。
要成为有理想的极客,我们不能停留在语法上,要掌握牢固的数学,概率,统计知识,同时还要有创新精神,把R语言发挥到各个领域。让我们一起动起来吧,开始R的极客理想。
关于作者:
- 张丹,分析师/程序员/Quant: R,Java,Nodejs
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-kmp/
前言
文字匹配是字符符处理操作时,最常用到的一种方法。比如我们想从一段长文本中,找到是否有我想要的词,可以用于在图书中用关键词进行搜索,这样就可以定位到具体的位置。当文本长度巨大,且匹配字符串长度过长时,这种匹配就会有效率问题,很变的很慢。
那么我们可以用KMP的算法思路,在提升文字精确匹配的效率。本文代码:https://github.com/bsspirit/r-string-match
目录
- 字符串匹配:暴力破解法
- KMP算法解释和实现
- KMP和暴力破解算法对比
1. 字符串匹配:暴力破解法
一般的字符串匹配算法,是将 2个字符串每个字符挨个进行比较,相当于是把每个字符都比较了一遍,做了对所有字符的组合,这样操作导致的时间复杂度是O(m*n),也就是 2 个字符串长度的积,俗称暴力解法。
我们设定原始字符串为:ABDABDZ ABCED,匹配字符串为:ABC。直接使用暴力法进行字符串匹配。
首先,建立暴力破解的字符串匹配函数bad_match(),包括4个参数。
- txt,原始文本的字符串
- pattern,匹配的字符串
- n,用于取匹配前几个,默认为0,表示全匹配
- LOGGER,用于显示日志
# 清空环境变量
> rm(list=ls())
# 设置运行目录
> setwd("C:/work/R/text")
# 建立字符串匹配函数:暴力破解法
> # 暴力破解法
> baoli_match<-function(txt,pattern,n=0,LOGGER=FALSE){
+ rs<-data.frame(start=0,end=0) # 默认返回值
+ start<-0 # 命中后在原始字符串的开始位置
+
+ n1<-nchar(txt) # 原始字符串长度
+ n2<-nchar(pattern) # 匹配的字符串长度
+
+ # 如果匹配的字符串为空,则返回
+ if(n2==0) return(r2)
+
+ # 初始化变量索引,i用于原始字符串,j用于匹配字符串
+ i<-j<-1
+ # 用于计数,循环了多少次
+ k<-0
+
+ # 循环计算
+ while(i < n1){
+
+ # 打印日志
+ if(LOGGER){
+ print(paste(i,j,substr(txt, i, i),substr(pattern, j, j),sep=","))
+ k<-k+1
+ }
+
+ # 匹配成功,同时移动
+ if(substr(txt,i,i) == substr(pattern,j,j)){
+ i<-i+1
+ j<-j+1
+ } else { # 匹配不成功,回到开始匹配的位置,重置i,j的索引
+ i<-i-(j-1)
+ i<-i+1
+ j<-1
+ }
+
+ # 把匹配到的,所有结果存到变量
+ if(j==(n2+1)) {
+ start<-append(start,i-n2)
+ j<-1
+
+ # 只取前面n个结果返回
+ if(n > 0 && n==length(start)-1){
+ break;
+ }
+ }
+ }
+
+ # 打印日志,输出循环了多少次
+ if(LOGGER){
+ print(paste("k",k,sep="="))
+ }
+
+ # 拼接返回值,为data.frame
+ if(length(start) > 1) {
+ start<-start[-1]
+ rs<-data.frame(start=start,end=start+n2-1)
+ }
+ return(rs)
+ }输出字符串,运行结果。
# 原始字符串
> txt<-"ABCCADZABCCABBC"
# 匹配字符串
> pattern<-"ABCCABB"
# 暴力匹配
> baoli_match(txt,pattern,LOGGER=TRUE)
[1] "1,1,A,A"
[1] "2,2,B,B"
[1] "3,3,C,C"
[1] "4,4,C,C"
[1] "5,5,A,A"
[1] "6,6,D,B"
[1] "2,1,B,A"
[1] "3,1,C,A"
[1] "4,1,C,A"
[1] "5,1,A,A"
[1] "6,2,D,B"
[1] "6,1,D,A"
[1] "7,1,Z,A"
[1] "8,1,A,A"
[1] "9,2,B,B"
[1] "10,3,C,C"
[1] "11,4,C,C"
[1] "12,5,A,A"
[1] "13,6,B,B"
[1] "14,7,B,B"
# 循环共20次
[1] "k=20"
# 匹配到1个结果,对应用到原始字符串的开始位置和结束位置
start end
1 8 14
2. KMP算法介绍
KMP 算法是一种改进的字符串匹配算法,由 D.E.Knuth,J.H.Morris 和 V.R.Pratt 提出的,因此人们称它为 Knuth-Morris-Pratt算法(简称KMP)。KMP 算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是通过一个 kmp_next () 函数实现,函数本身包含了模式串的局部匹配信息。KMP 算法的时间复杂度O(m+n)。
建立kmp_next() 函数,匹配字符串的最长公串。
# 建立匹配字符串的最长公串
> kmp_next <- function(patten,LOGGER=FALSE) {
+ n <- nchar(patten)
+ nxt <- rep(0, n)
+ i <- 2
+ j <- 1
+ while (i < n) {
+ if(LOGGER){
+ print(paste(i,j,substr(patten, i, i),substr(patten, j, j),sep=","))
+ }
+ if (substr(patten, i, i) == substr(patten, j, j)) {
+ nxt[i] <- j
+ i = i + 1
+ j = j + 1
+ } else{
+ if (j > 1) {
+ j = nxt[j - 1]
+ }
+ else{
+ nxt[i] = 0
+ i = i + 1
+ }
+ }
+ }
+ nxt
+ }
运行计算结果,ABC的最长公串为0,ABCCABB最长公串,为1和2。
> kmp_next("ABC")
[1] 0 0 0
> kmp_next("ABCCABB")
[1] 0 0 0 0 1 2 0
建立KMP算法函数,使用kmp_next()最长公串的结果,减少循环的次数。
> kmp_match<-function(txt, patten, n=0, LOGGER=FALSE) {
+ rs<-data.frame(start=0,end=0) # 默认返回值
+ start<-0 # 命中后在原始字符串的开始位置
+ n1<-nchar(txt) # 原始字符串长度
+ n2<-nchar(pattern) # 匹配的字符串长度
+
+ # 如果匹配的字符串为空,则返回
+ if(n2==0) return(rs)
+
+ nxt<-kmp_next(patten) #获取next最长公串
+
+ # 初始化变量索引,i用于原始字符串,j用于匹配字符串
+ i<-j<-1
+ # 用于计数,循环了多少次
+ k<-0
+
+ # 循环计算
+ while(i1) j<-nxt[j-1]+1
+ else i<-i+1
+ }
+
+ if(j==(n2+1)) {
+ start<-append(start,i-n2)
+ j<-1
+
+ if(n>0 && n==length(start)-1){
+ break;
+ }
+ }
+ }
+
+ # 打印日志,输出循环了多少次
+ if(LOGGER){
+ print(paste("k",k,sep="="))
+ }
+
+ # 拼接返回值,为data.frame
+ if(length(start)>1) {
+ start<-start[-1]
+ rs<-data.frame(start=start,end=start+n2-1)
+ }
+ return(rs)
+ }
运行KMP算法,使用暴力破解法同样的参数,发现循环计算只运行了14次,比暴力破解法少了2次。
> txt<-"ABCCADZABCCABBC"
> pattern<-"ABCCABB"
> kmp_match(txt,pattern,LOGGER=TRUE)
[1] "pattern:ABCCABB,next:0000120"
[1] "1,1,A,A"
[1] "2,2,B,B"
[1] "3,3,C,C"
[1] "4,4,C,C"
[1] "5,5,A,A"
[1] "6,6,D,B"
[1] "6,2,D,B"
[1] "6,1,D,A"
[1] "7,1,Z,A"
[1] "8,1,A,A"
[1] "9,2,B,B"
[1] "10,3,C,C"
[1] "11,4,C,C"
[1] "12,5,A,A"
[1] "13,6,B,B"
[1] "14,7,B,B"
# 循环共16次
[1] "k=16"
# 匹配到1个结果,对应用到原始字符串的开始位置和结束位置
start end
1 8 14
3. KMP和暴力破解算法对比
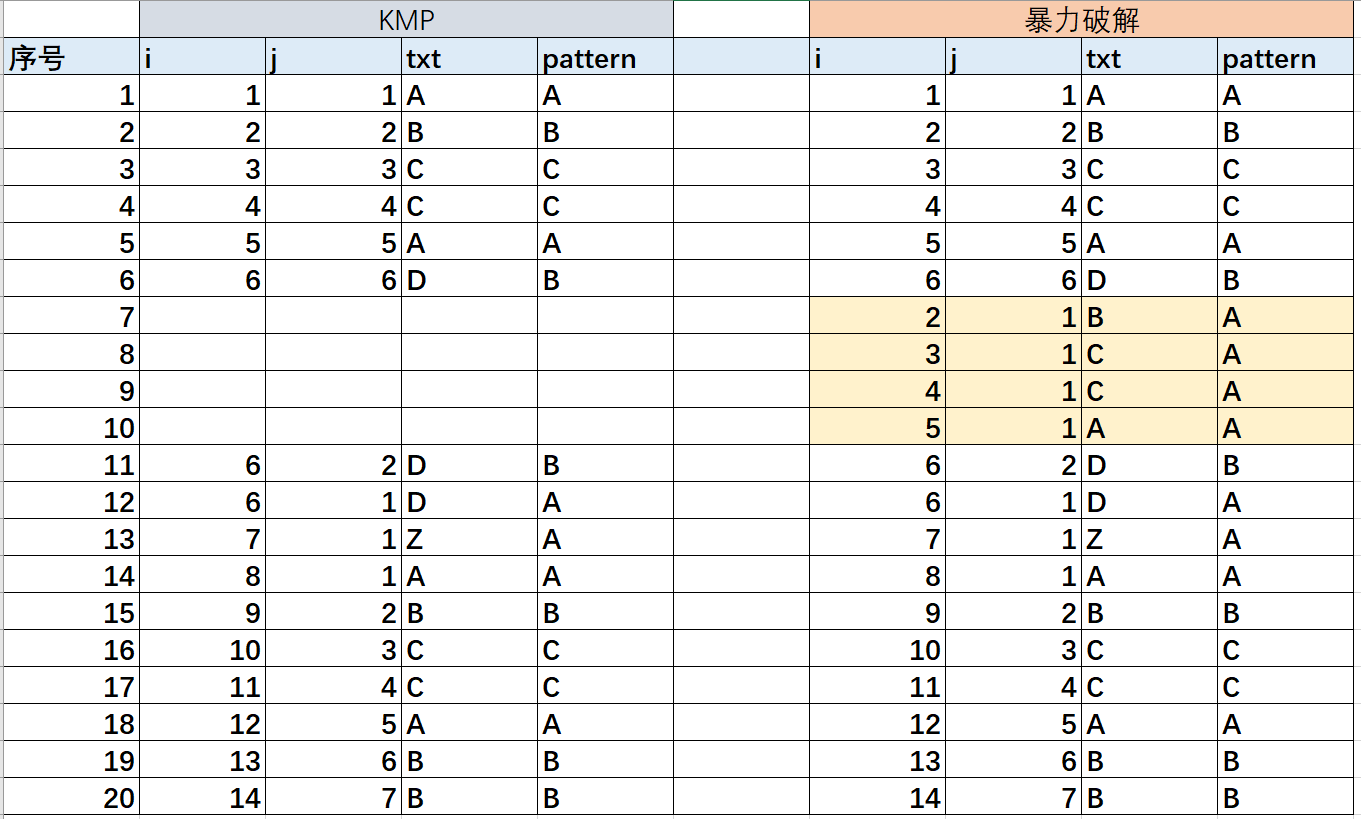
我们对比一下暴力破解法 和 KMP算法,具体的差异在什么问题,为什么能少算4次。
从下面循环对比的图中,我们可以明确的看到KMP算法,少的原因在于出现的匹配不一致时,暴力匹配是让匹配字符串回到1重新开始匹配,而KMP算法则是利用了next的最大公共串,找到上一个公共串的位置,这样就可以大幅提升遍历的效率。
KMP算法的原理的参考文献:阮一峰:字符串匹配的KMP算法
虽然R语言不擅长写算法,且while循环的性能也不高,但是如果能大幅减少循环的计算次数,也是一种不错的解决方案。自己写了一套字符串匹配的代码已经放到了github:https://github.com/bsspirit/r-string-match
一点一点的优化,从算法层搞起。
转载请注明出处:
http://blog.fens.me/r-kmp/