算法为王系列文章,涵盖了计算机算法,数据挖掘(机器学习)算法,统计算法,金融算法等的多种跨学科算法组合。在大数据时代的背景下,算法已经成为了金字塔顶的明星。一个好的算法可以创造一个伟大帝国,就像Google。
算法为王的时代正式到来….
关于作者:
- 张丹, 分析师/程序员/Quant: R,Java,Nodejs
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-graph-shortest-path-dijkstra/
前言
最短路径是图算法中的基本算法,被普遍应用于多种场景中,比如在实际生活中的路径规划、地图导航,建立道路交通网、物流运输网络、计算机网络等,这时就可以使用最短路径算法。
常用的最短路径算法包括:Dijkstra算法,A star算法,Bellman-Ford算法,SPFA算法(Bellman-Ford算法的改进版本),Floyd-Warshall算法,Johnson算法以及Bi-direction BFS算法。
目录
- 最短路径算法介绍
- Dijkstra 算法原理
- 用R语言调用 Dijkstra 算法
1. 最短路径算法介绍
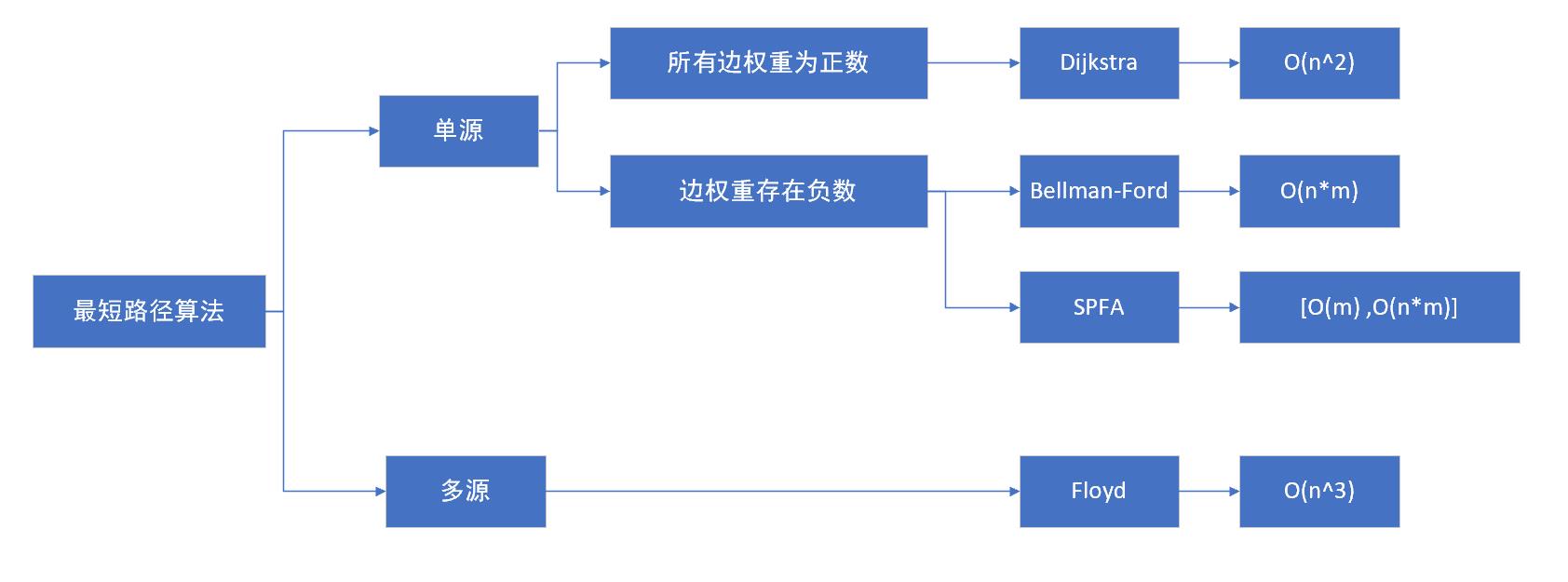
最短路径问题是图论研究中一个经典算法问题,旨在寻找图中两节点或单个节点到其他节点之间的最短路径。根据问题的不同,算法的具体形式包括:
- 确定起点的最短路径问题,即给定起始节点,求该节点到其他剩余节点的最短路径,适合使用Dijkstra算法
- 确定终点的最短路径问题,即给定终点,求其他节点到该终点的最短路径。在无向图中,该问题与确定起点的问题等价;在有向图中,问题等价于把所有路径方向反转的确定起点的问题;
- 确定起点终点的最短路径问题,即给定起点和终点,求两节点之间的最短路径;
- 全局最短路径问题,即求图中所有节点之间的最短路径,适合使用Floyd-Warshall算法。
| 最短路径算法 | 描 述 |
|---|---|
| 迪杰斯特拉算法 (Dijkstra) | 寻找某个特定顶点到其它所有顶点的最短路径,该算法要求所有路径的权值为非负数。 |
| 贝尔曼福特算法 (Bellman-Ford) | 寻找某个特定顶点到其它所有顶点的最短路径,该算法允许路径的权值为负数。 |
| 弗洛伊德算法 (Floyd-Warshall) | 寻找各个顶点之间的最短路径,允许非环路的路径权值为负数,该算法不仅适用于稀疏图,在稠密图(路径数量多的图)中寻找最短路径的效率也很高。 |
| 约翰逊算法 (Johnson) | 寻找各个顶点之间的最短路径,允许非环路的路径权值为负数,该算法更适用于稀疏图(路径数量少的图)。 |
2. Dijkstra 算法原理
Dijkstra算法,于1956年由荷兰计算机科学家艾兹赫尔.戴克斯特拉提出,用于解决赋权有向图的单源最短路径问题。所谓单源最短路径问题是指确定起点,寻找该节点到图中任意节点的最短路径,算法可用于寻找两个城市中的最短路径或是解决著名的旅行商问题。
基本思想
- 通过Dijkstra计算图中的最短路径时,需要指定一个起点A。
- 简历两个数组S和U,S用于记录已求出最短路径的顶点(以及相应的最短路径长度),U用于记录还未求出最短路径的顶点(以及该顶点到起点A的距离)。
- 初始时,数组S中只有起点A;数组U中是除起点A之外的顶点,并且数组U中记录各顶点到起点A的距离。如果顶点与起点A不相邻,距离为无穷大INF。
- 从数组U中找出路径最短的点X,并将其加入到数组S中;同时,从数组U中移除顶点X。接着,更新数组U中的各顶点到起点A的距离。
- 重复第4步操作,直到遍历完所有顶点。
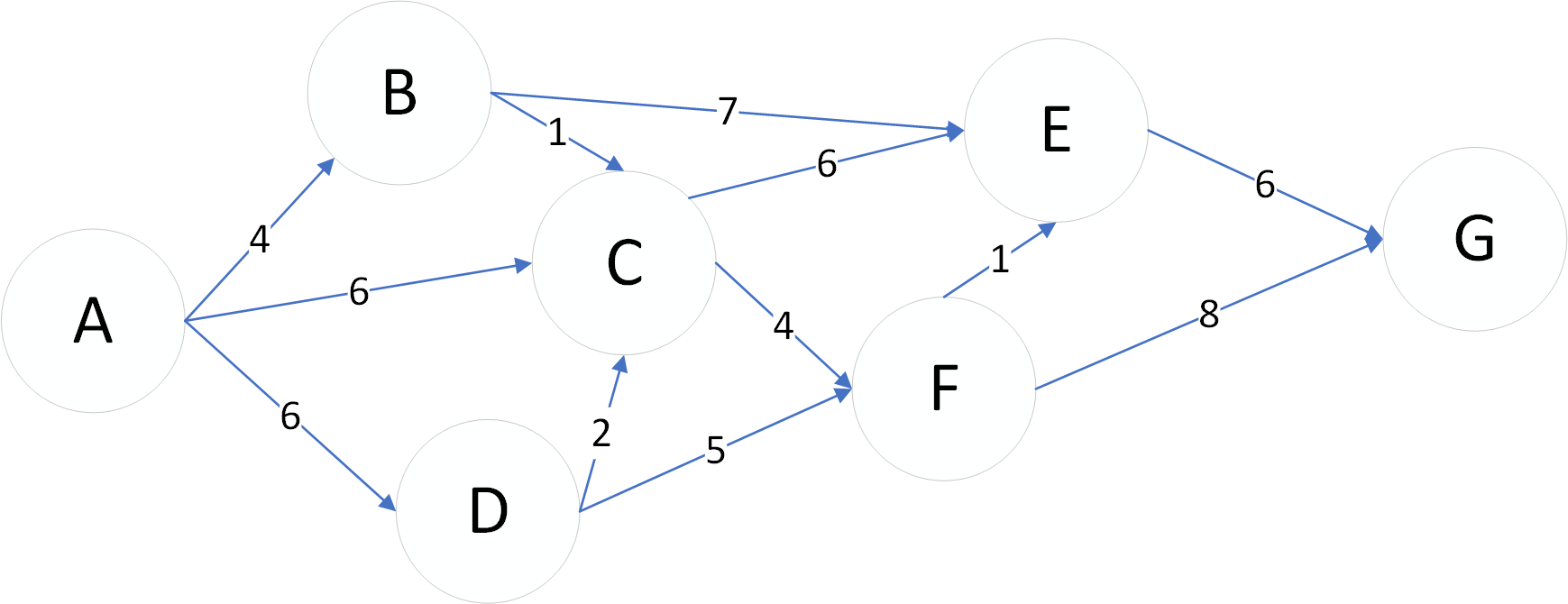
下面,我们来举例说明一下算法,创建一个带权重的有向图,来描述对最短路径。
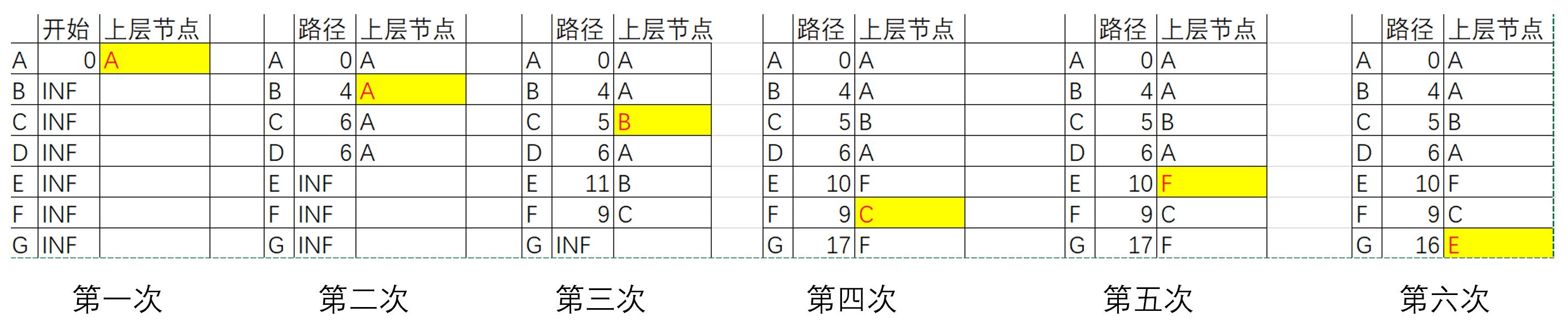
开始点为A,数组U为开始列,数组S为上层节点列。通过6次遍历,找到从A到G的最短路径。
3. 用R语言调用 Dijkstra 算法
我们用R语言中,igraph包已经实现了Dijkstra算法,我们可以直接调用igraph包的shortest.pahs()函数进行最短路径的计算。首先,安装和加载 igraph 程序包
> install.pacakges("igraph")
> library(igraph)
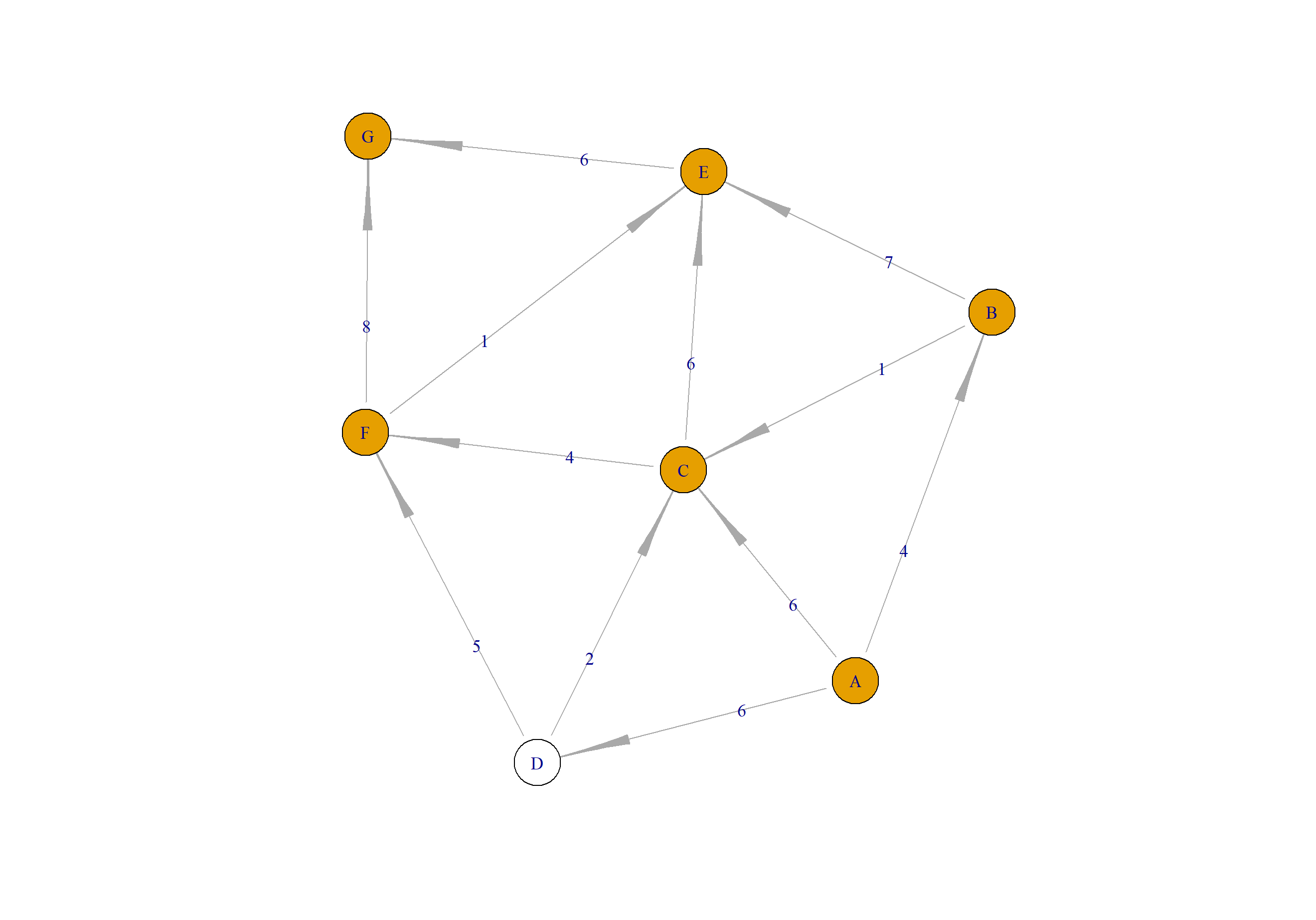
生一个有向有权重的网络图,如上例所示。
> df<-data.frame(
+ from=c("A","A","A","B","D","B","C","D","C","F","E","F"),
+ to=c("B","D","C","C","C","E","E","F","F","E","G","G"),
+ weight=c(4,6,6,1,2,7,6,5,4,1,6,8)
+ )
> df
from to weight
1 A B 4
2 A D 6
3 A C 6
4 B C 1
5 D C 2
6 B E 7
7 C E 6
8 D F 5
9 C F 4
10 F E 1
11 E G 6
12 F G 8
把数据生成igraph图对象,再以网络图进行展示。
# 生成igraph对象
> a<-graph_from_data_frame(df, directed = TRUE, vertices = NULL)
# 画图
> E(a)$arrow.size<-1
> E(a)$arrow.width<-0.2
> E(a)$label<-df$weight
> plot(a)
上面我们把节点涂色了,下面继续把边也涂色。首先,找到最短路径上的边,把最短路径边涂红色,非最短路径的边涂灰色。
# 通过最短路径的节点,建立边的关系
> s_vert<-data.frame(from=s_node[-length(s_node)],to=s_node[-1])
# 找到网络图中所有的边
> a_vert<-as_data_frame(a,what="edges")
# 找到最短路径的边的索引
> idx<-which(paste0(a_vert$from,"-",a_vert$to) %in% paste0(s_vert$from,"-",s_vert$to))
> idx
[1] 1 4 9 10 11
# 涂色:红色为最短路径的边,灰色为非最短路径的边
> a_vert$color<-"gray"
> a_vert$color[idx]<-"red"
# 画图
> E(a)$color<-a_vert$color
> plot(a)
用Dijkstra算法,计算从A开始,到B,C,D,E,F,G的所有节点的最短距离。
> shortest.paths(a,"A", algorithm = "dijkstra")
A B D C F E G
A 0 4 6 5 9 10 16
输出结果,从A到B最短距离为4,从A到D最短距离为6,从A到C最短距离为5,从A到F最短距离为9,从A到E最短距离为10,从A到G最短距离为16。
当然,我们除了想知道最短距离,还想知道最短距离的路径是什么样的。接下来,我们先计算最短距离路径上的点,并发点进行涂色。
# 计算最短距离经过的点
> s_node<-all_shortest_paths(a,"A","G")$res[[1]]$name
> snode
[1] "A" "B" "C" "F" "E" "G"
# 把节点进行涂色
> cols<-data.frame(label=V(a)$name,color=0)
> cols$color[which(cols$label %in% s_node)]<-1
> cols
label color
1 A 1
2 B 1
3 D 0
4 C 1
5 F 1
6 E 1
7 G 1
# 画图
> V(a)$color<-cols$color
> plot(a)
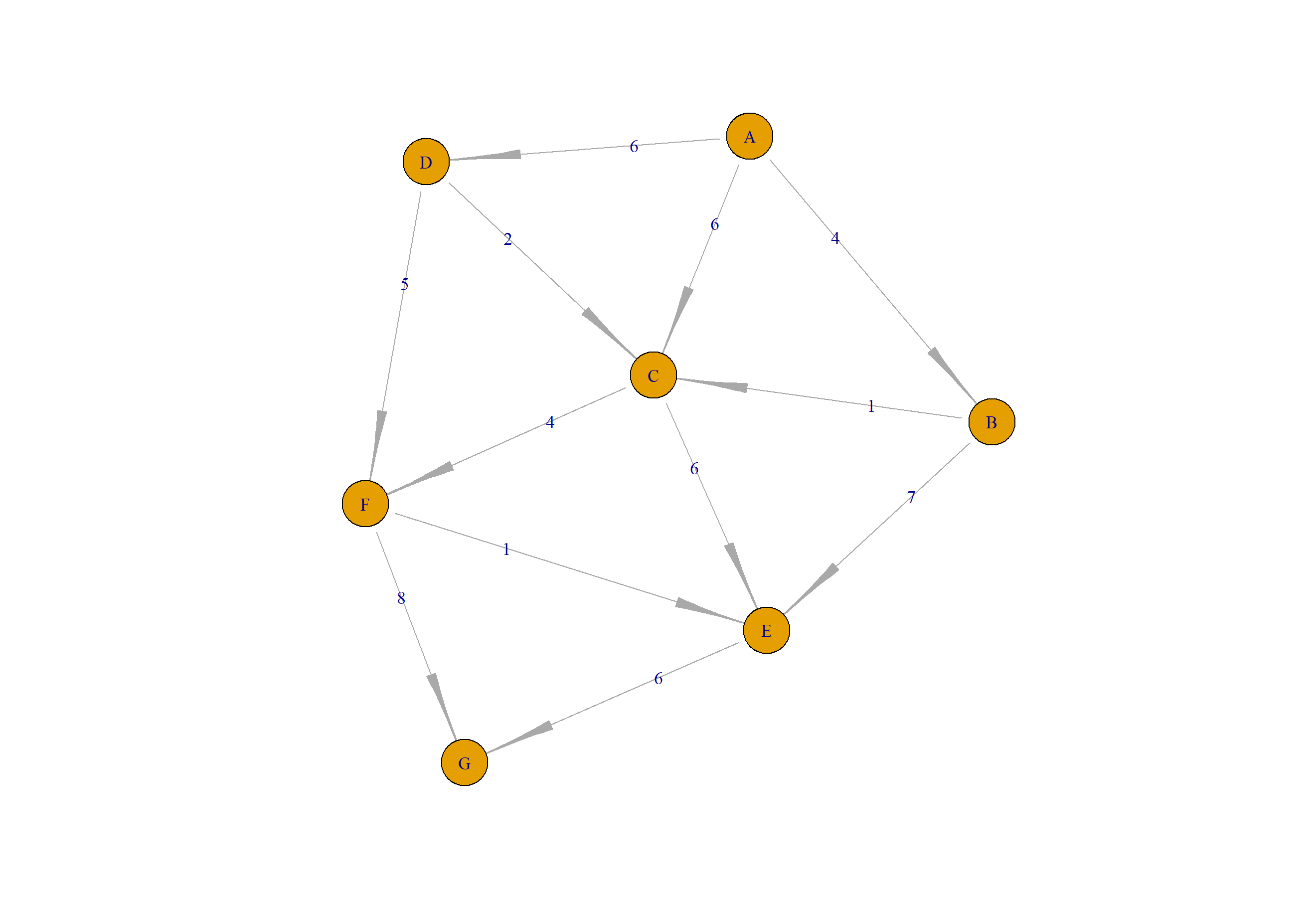
其中,黄色点为最短距离穿过的节点,白色节点为不在最短距离路径上的节点。
上面我们把点进行了涂色,下面我们继续边最少路径的边进行涂色。首先,根据最短路径的节点,创建边的关系。然后对边进行涂色,在最短路径的边涂为红色,不在最短路径的边涂为灰色。
# 建立最短路径节点的关系
> s_vert<-data.frame(from=s_node[-length(s_node)],to=s_node[-1])
# 找到网络图的完整路径
> a_vert<-as_data_frame(a,what="edges")
# 找到最短路径的边的索引
> idx<-which(paste0(a_vert$from,"-",a_vert$to) %in% paste0(s_vert$from,"-",s_vert$to))
> idx
[1] 1 4 9 10 11
# 涂色
> a_vert$color<-"gray"
> a_vert$color[idx]<-"red"
# 画图
> E(a)$color<-a_vert$color
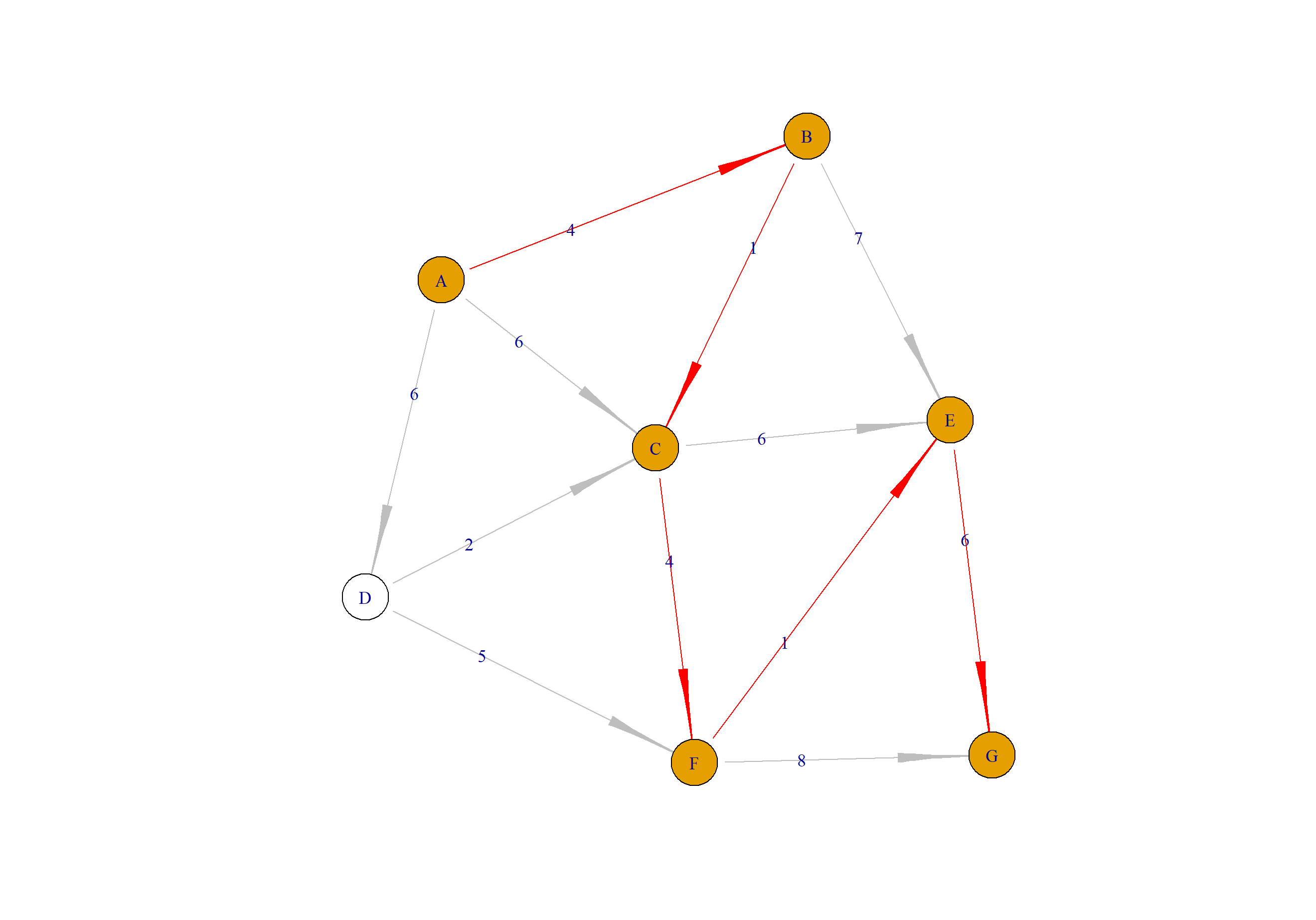
> plot(a)
这样就在完整的网络图中,可以从开始节点A,按红色路径走到G,生成了最短路径所过过的节点和边了。
扩展一下,我们用Dijkstra算法,分别计算从不同点开始,到所有不同的点的最短距离,通过矩阵来表达,任意2个节点的最短距离。
> shortest.paths(a, algorithm = "dijkstra")
A B D C F E G
A 0 4 6 5 9 10 16
B 4 0 3 1 5 6 12
D 6 3 0 2 5 6 12
C 5 1 2 0 4 5 11
F 9 5 5 4 0 1 7
E 10 6 6 5 1 0 6
G 16 12 12 11 7 6 0
通过上面的步骤,我们就实现了在R语言中使用Dijkstra算法,计算的最短路径算法。本来还想着,自己再来实现一遍,发现网上有很多的开源的代码,还让自己休息一下吧。下篇文章将介绍,知识图谱:最短路径算法Bellman-Ford算法,应该是需求自己手写了。
本文算法代码已上传到github: https://github.com/bsspirit/graph/blob/main/dijkstra.r
转载请注明出处:
http://blog.fens.me/r-graph-shortest-path-dijkstra/