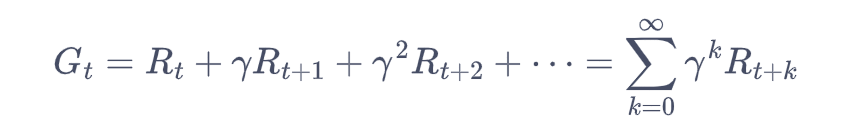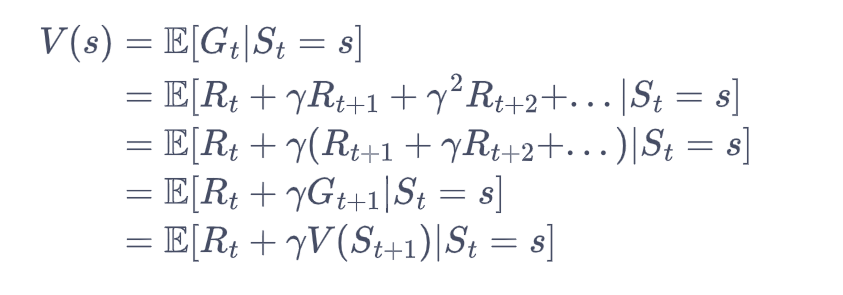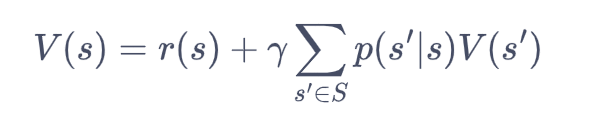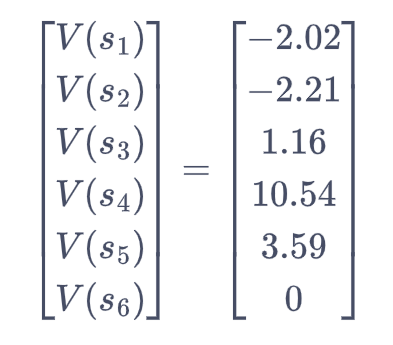R的极客理想系列文章，涵盖了R的思想，使用，工具，创新等的一系列要点，以我个人的学习和体验去诠释R的强大。

R语言作为统计学一门语言，一直在小众领域闪耀着光芒。直到大数据的爆发，R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入，R语言的社区在迅速扩大成长。现在已不仅仅是统计领域，教育，银行，电商，互联网….都在使用R语言。

要成为有理想的极客，我们不能停留在语法上，要掌握牢固的数学，概率，统计知识，同时还要有创新精神，把R语言发挥到各个领域。让我们一起动起来吧，开始R的极客理想。

关于作者：

• 张丹，分析师/程序员/Quant: R,Java,Nodejs
• blog: http://blog.fens.me
• email: bsspirit@gmail.com

转载请注明出处：
http://blog.fens.me/r-markov/

前言

马尔科夫决策过程是强化学习的数学框架基础，通过状态、动作、奖励和状态转移概率的形式化描述，为智能体提供了与环境交互的理论模型。在强化学习中，MDP为价值函数、策略优化和贝尔曼方程等关键概念提供了理论基础，是理解Q学习、策略梯度等算法的重要前提，帮助智能体学习在不确定环境中做出最优决策。

新的方向，开始强化学习的学习。

目录

1. 马尔可夫(Markov)决策过程介绍
2. 用R语言实现马尔可夫链

1. 马尔可夫(Markov)决策过程介绍

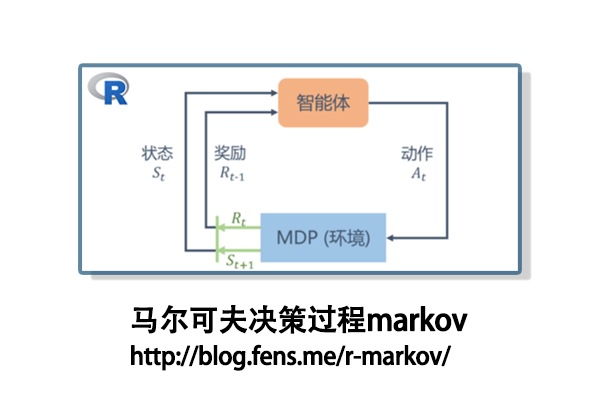
马尔可夫决策过程（Markov decision process, MDP），是一种关于事件发生的概率预测方法。它是根据事件的目前状况来预测其将来各个时刻（或时期)变动状况的一种预测方法。马尔可夫决策过程包含一组交互对象，即智能体（agent）和环境，并定义了5个模型要素：状态（state）、动作（action）、策略（policy）、奖励（reward）和回报（return），其中策略是状态到动作的映射，回报是奖励随时间步的折现或积累。

马尔可夫决策过程于随机过程领域，随机过程与概率论中静态的随机现象不同，随机过程的研究对象是随时间演变的随机现象（例如天气随时间的变化、城市交通随时间的变化）。在随机过程中，随机现象在某时刻的取值是一个向量随机变量，用表示，所有可能的状态组成状态集合。随机现象便是状态的变化过程。在某时刻的状态St通常取决于t时刻之前的状态。

状态转移

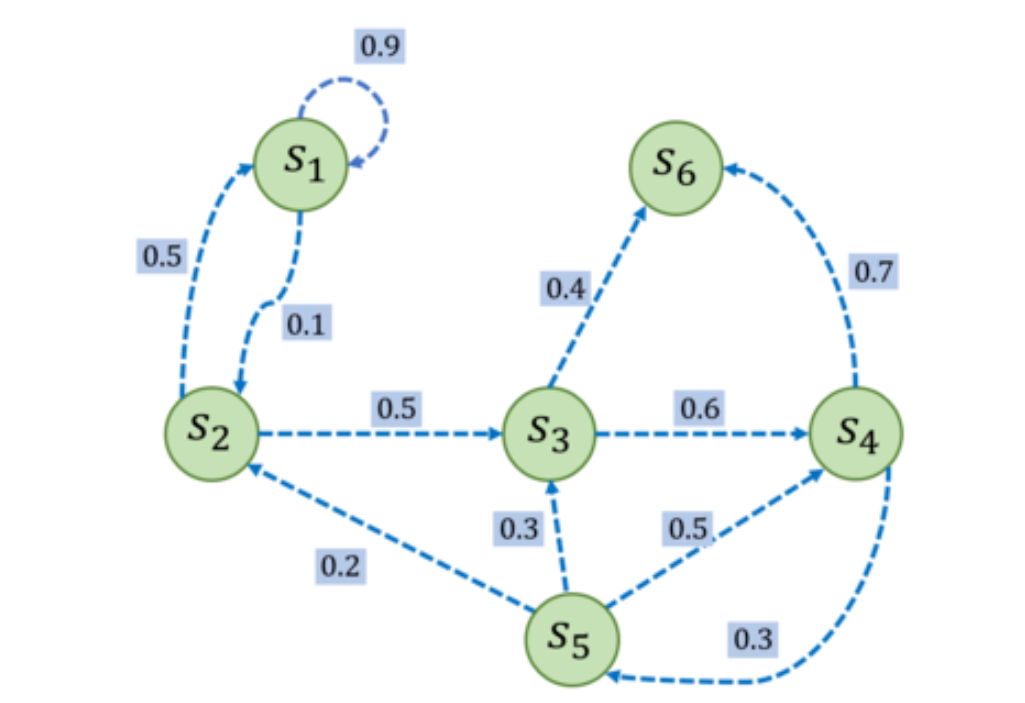
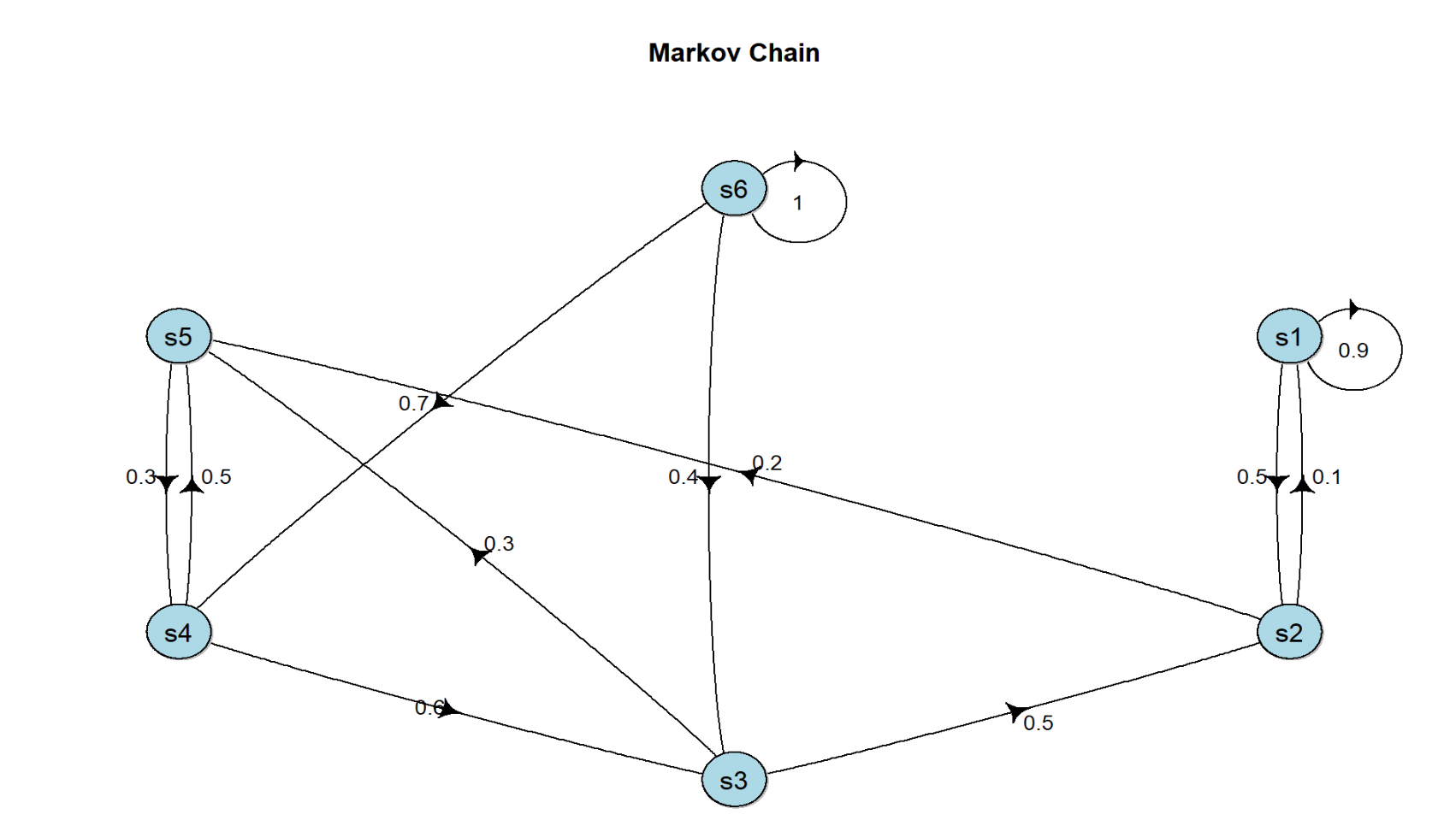
马尔可夫过程举例，一个具有 6 个状态的马尔可夫过程的例子。

其中每个绿色圆圈（s1-s6）表示一个状态，每个状态都有一定概率（包括概率为 0）转移到其他状态。其中s6 被称为终止状态，它不再转出到其他状态。状态之间的虚线箭头表示状态的转移，箭头旁的数字表示该状态转移发生的概率。从每个状态出发转移到其他状态的概率总和为 1。例如，有s1有 90%概率到自己保持不变，s1有 10%概率转移到s2。而在s2又有 50%概率回到s1，s2有 50%概率转移到s3。

把上面的状态转移过程，用矩阵表示，即状态转移矩阵。其中，矩阵第i行j列的值，则代表从状态Si转移到Sj的概率。

给定一个马尔可夫过程，我们就可以从某个状态出发，根据它的状态转移矩阵生成一个状态序列（episode），这个步骤也被叫做采样（sampling）。例如，从S1出发，可以生成序列S1->S2->S3->S6，或S1->S1->S2->S3->S4->S5->S3->S6等。生成这些序列的概率和状态转移矩阵有关。

马尔可夫的奖励过程

在马尔可夫过程的基础上加入奖励函数r 和 折扣因子γ，就可以得到马尔可夫奖励过程（Markov reward process）。一个马尔可夫奖励过程由(S,P,r,γ)构成，各个组成元素的含义如下所示。

• S是有限状态的集合。
• P是状态转移矩阵。
• r是奖励函数，某个状态s的奖励r(s) 指转移到该状态时可以获得奖励的期望。
• γ是折扣因子（discount factor），γ的取值范围为[0,1)。引入折扣因子的理由为远期利益具有一定不确定性，有时我们更希望能够尽快获得一些奖励，所以我们需要对远期利益打一些折扣。接近 1 的γ更关注长期的累计奖励，接近 0 的γ更考虑短期奖励。

回报的计算：在一个马尔可夫奖励过程中，从第t时刻状态St开始，直到终止状态时，所有奖励的衰减之和称为回报Gt（Return）。

计算公式：

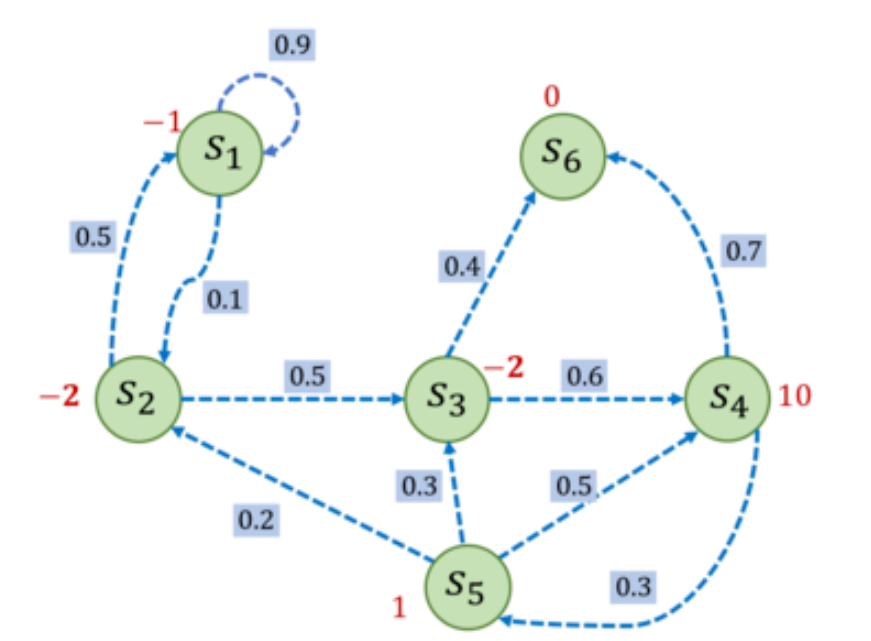
其中，Rt表示在时刻t获得的奖励。对马尔可夫过程添加奖励函数，构建成一个马尔可夫奖励过程。例如，进入状态s2可以得到-2奖励，表明我们不希望进入s2。进入s4可以获得最高的奖励10，但是进入s6之后奖励为0，并且此时序列也终止了。

手动计算G1的奖励，选取s1为起始状态，设置γ=0.5，采样到一条状态序列为s1->s2->s3->s6，就可以计算s1的回报G1=-2.5，得到 G1 = -1 + 0.5*(-2) + 0.5^2*(-2) = -2.5。

状态价值计算

在马尔可夫奖励过程中，一个状态的期望回报（即从这个状态出发的未来累积奖励的期望）被称为这个状态的价值（value）。所有状态的价值就组成了价值函数（value function），价值函数的输入为某个状态，输出为这个状态的价值。

计算公式：V(s)为价值，Gt为某个状态的回报。

在上式的最后一个等号中，一方面，即时奖励的期望正是奖励函数的输出，另一方面，等式中剩余部分可以根据从状态出发的转移概率得到。获得马尔可夫奖励过程中非常有名的贝尔曼方程（Bellman equation）。

求解得到各个状态的价值V(s)，

我们现在用贝尔曼方程来进行简单的验证。例如，对于状态s4来说，当γ=0.5时，则

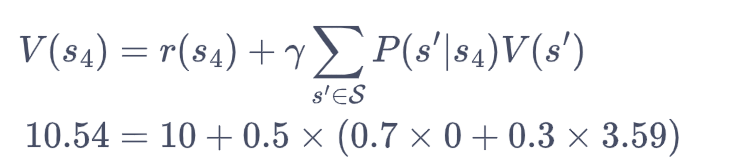
可以发现左右两边的值是相等的，说明我们求解得到的价值函数是满足状态为时的贝尔曼方程。

参考文章：https://hrl.boyuai.com/chapter/1/马尔可夫决策过程/

2. 用R语言实现马尔可夫链

我们用R语言模拟上面的整个马尔可夫决策的计算过程，先使用手搓的方法，后面再掉包实现。

2.1 马尔可夫过程

首先，定义状态集合s，共6种状态 s1,s2,s3,s4,s5,s6。

# 6种状态
> s <- c("s1", "s2", "s3", "s4", "s5", "s6")
> s
[1] "s1" "s2" "s3" "s4" "s5" "s6"

定义转移概率矩阵p

> p <- matrix(c(
+   0.9,0.1,  0,  0,  0,  0,
+   0.5,  0,0.5,  0,  0,  0,
+     0,  0,  0,0.6,  0,0.4,
+     0,  0,  0,  0,0.3,0.7,
+     0,0.2,0.3,0.5,  0,  0,
+     0,  0,  0,  0,  0,  1
+ ), nrow = 6, byrow = TRUE, dimnames = list(s, s))

查看矩阵结果 
> p
    s1  s2  s3  s4  s5  s6
s1 0.9 0.1 0.0 0.0 0.0 0.0
s2 0.5 0.0 0.5 0.0 0.0 0.0
s3 0.0 0.0 0.0 0.6 0.0 0.4
s4 0.0 0.0 0.0 0.0 0.3 0.7
s5 0.0 0.2 0.3 0.5 0.0 0.0
s6 0.0 0.0 0.0 0.0 0.0 1.0

画图转移概率矩阵

> library(diagram)
> plotmat(p,lwd = 1, box.lwd = 1, cex.txt = 0.8, 
+         box.size = 0.02, box.type = "circle", shadow.size = 0.001,
+         box.col = "light blue",  arr.length=0.1, arr.width=0.1,
+         self.cex = 1.5,self.shifty = -0.01,self.shiftx = 0.04, 
+         main = "Markov Chain")

模拟随机的状态转移过程。

# 模拟马尔科夫链的函数
> simulate_markov_chain <- function(transition_matrix, initial_state, n_steps, stop=NULL) {
+   states <- rownames(transition_matrix)
+   chain <- character(n_steps + 1)
+   chain[1] <- initial_state
+   
+   for (i in 1:n_steps) {
+     current_state <- chain[i]
+     next_state <- sample(states, size = 1, prob = transition_matrix[current_state, ])
+     chain[i + 1] <- next_state
+   }
+   
+   # 停止状态
+   if(!is.null(stop)){
+     chain<-chain[1:which(chain==stop)[1]]  
+   }
+   
+   return(chain)
+ }

模拟马尔科夫链的结果。

# 设置初始状态和步数
> initial_state <- "s1" # 初始状态
> n_steps <- 300        # 执行步数
> stop_state<-'s6'      # 结束状态
> markov_chain <- simulate_markov_chain(p, initial_state, n_steps,stop_state)
> markov_chain
[1] "s1" "s1" "s1" "s1" "s1" "s2" "s3" "s6"

# 再次随机模拟结果
> markov_chain <- simulate_markov_chain(p, initial_state, n_steps)
> markov_chain
[1] "s1" "s1" "s1" "s2" "s3" "s4" "s5" "s4" "s6"

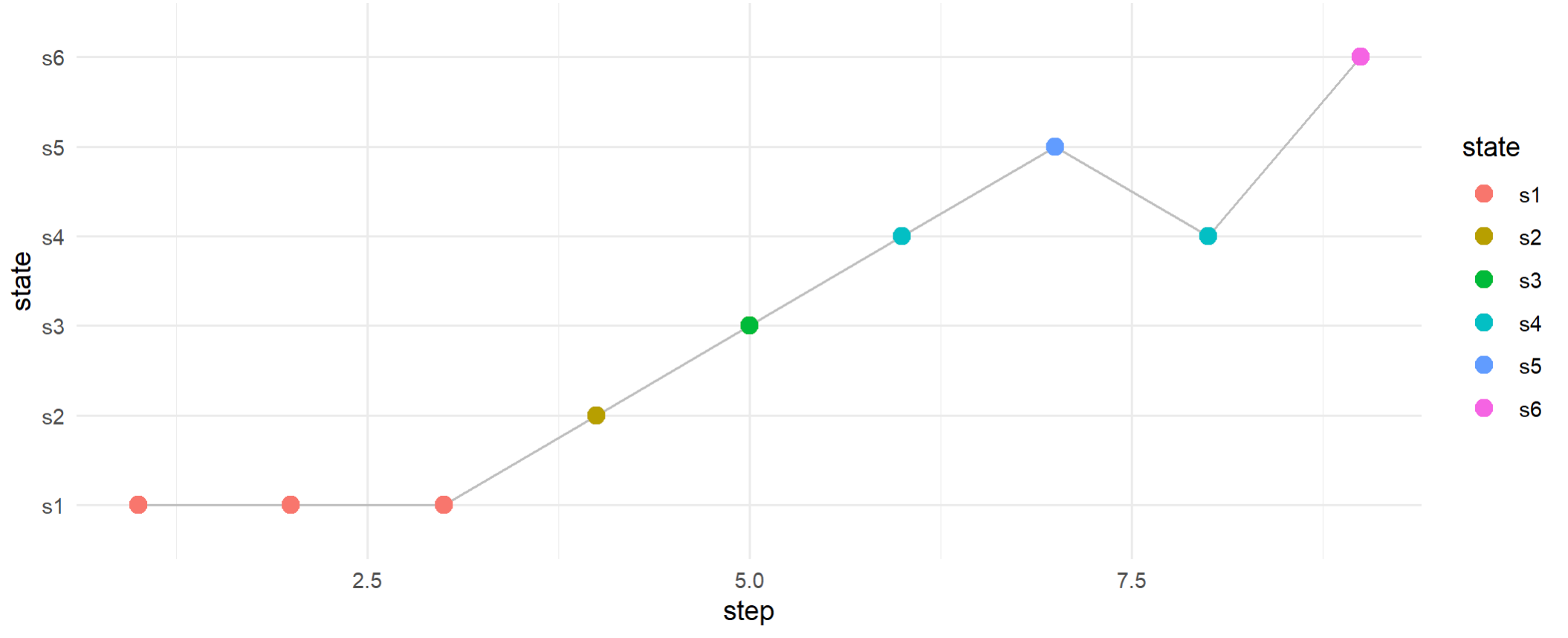
可视化展示马尔科夫链过程

> library(ggplot2)
> library(dplyr)
 
> # 准备数据用于绘图
> chain_df <- data.frame(
+     step = 1:length(markov_chain),
+     state = factor(markov_chain, levels = s)
+ )
 
> # 绘制马尔科夫链路径
> ggplot(chain_df, aes(x = step, y = state, group = 1)) +
+     geom_line(color = "gray") +
+     geom_point(aes(color = state), size = 3) +
+     theme_minimal()

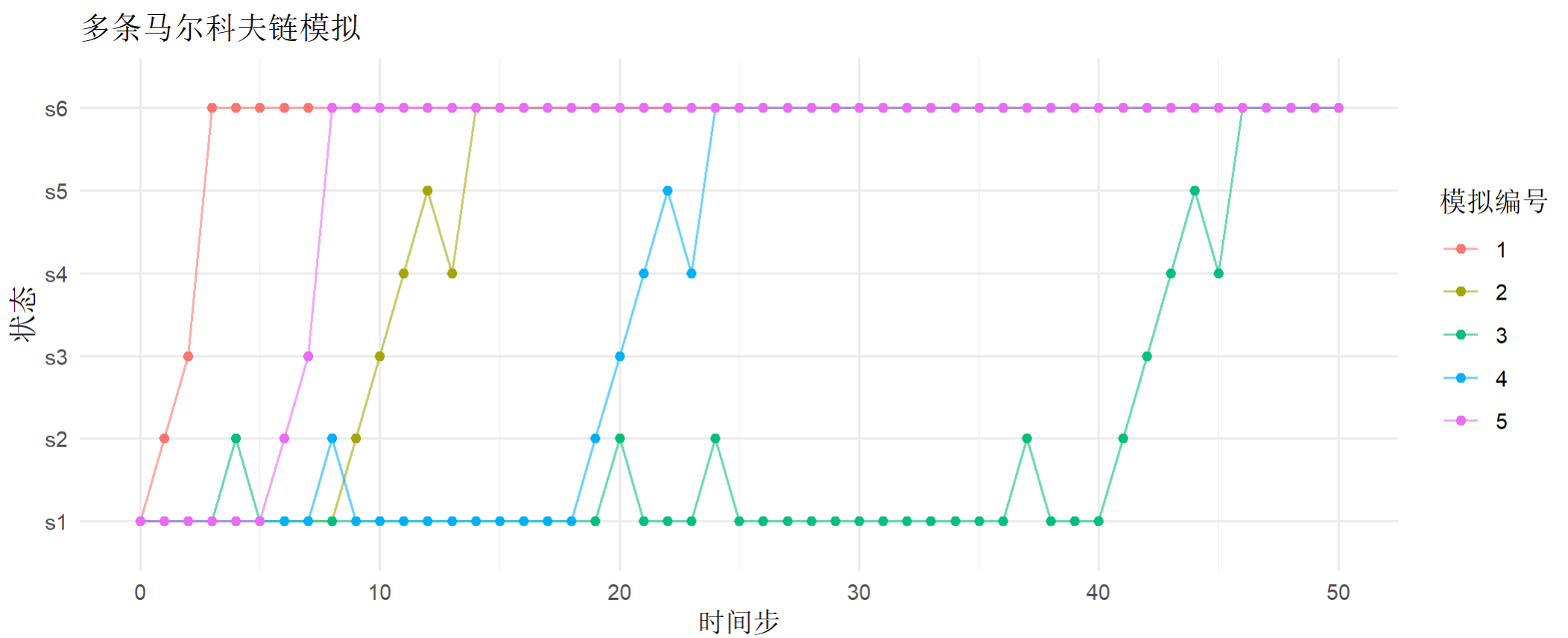
模拟多条马尔科夫链观察收敛性

# 5条路径
> n_simulations <- 5
> n_steps <- 50
> simulations <- list()

> for (i in 1:n_simulations) {
+   simulations[[i]] <- simulate_markov_chain(p, initial_state, n_steps)
+ }

# 准备数据用于绘图
> sim_df <- data.frame(
+   step = rep(0:n_steps, n_simulations),
+   state = unlist(simulations),
+   simulation = rep(1:n_simulations, each = n_steps + 1)
+ )

# 绘制多条马尔科夫链
> ggplot(sim_df, aes(x = step, y = state, group = simulation, color = factor(simulation))) +
+   geom_line(alpha = 0.6) +
+   geom_point(size = 1.5) +
+   labs(title = "多条马尔科夫链模拟",
+        x = "时间步", y = "状态",
+        color = "模拟编号") +
+   theme_minimal()

我们模拟了5条路径的马尔科夫链

计算马尔科夫链的稳态分布

# 计算稳态分布
> calculate_steady_state <- function(transition_matrix, tolerance = 1e-6) {
+   n_states <- nrow(transition_matrix)
+   # 初始猜测
+   pi <- rep(1/n_states, n_states)
+   
+   while (TRUE) {
+     pi_new <- pi %*% transition_matrix
+     if (max(abs(pi_new - pi)) < tolerance) break
+     pi <- pi_new
+   }
+   
+   return(as.vector(pi_new))
+ }

> steady_state <- calculate_steady_state(p)
> names(steady_state) <- s

# 稳态分布:
> steady_state
          s1           s2           s3           s4           s5           s6 
1.663447e-05 1.794239e-06 1.016132e-06 7.652676e-07 2.406675e-07 9.999795e-01

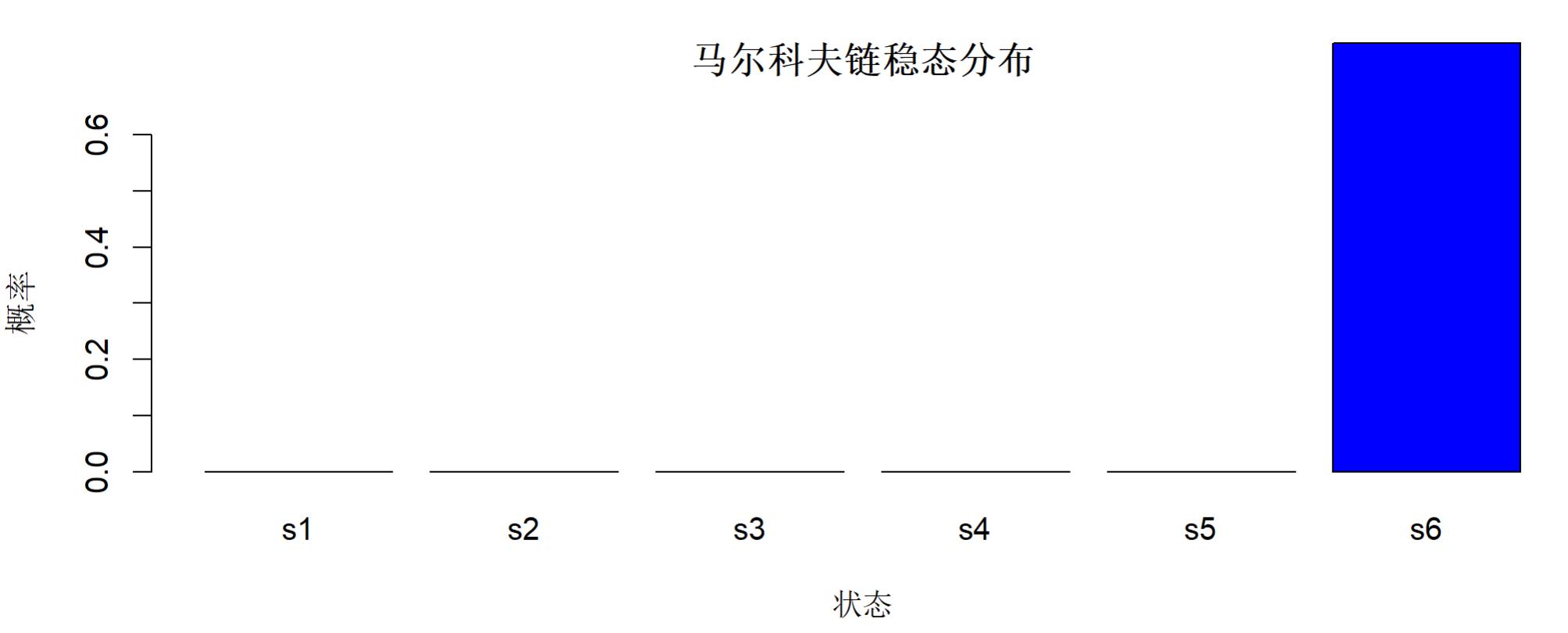
# 可视化稳态分布
> barplot(steady_state, col = c("gold", "gray", "blue"),
+         main = "马尔科夫链稳态分布",
+         ylab = "概率", xlab = "状态",
+         ylim = c(0, 0.6))

2.2 马尔可夫奖励过程

奖励过程：为每个状态定义了即时奖励，模拟了带奖励的马尔科夫链，并计算了总奖励和折现奖励。

编写带奖励的马尔科夫链函数，用于奖励计算。

# 模拟带奖励的马尔科夫链
> simulate_markov_reward <- function(transition_matrix, rewards, initial_state, n_steps, gamma = 0.9, stop=NULL) {
+     states <- rownames(transition_matrix)
+     chain <- character(n_steps + 1)
+     reward_sequence <- numeric(n_steps + 1)
+     discounted_rewards <- numeric(n_steps + 1)
+     
+     chain[1] <- initial_state
+     reward_sequence[1] <- rewards[initial_state]
+     discounted_rewards[1] <- (gamma^0) * rewards[initial_state]
+     
+     for (i in 1:n_steps) {
+         current_state <- chain[i]
+         next_state <- sample(states, size = 1, prob = transition_matrix[current_state, ])
+         chain[i + 1] <- next_state
+         reward_sequence[i + 1] <- rewards[next_state]
+         discounted_rewards[i + 1] <- (gamma^i) * rewards[next_state]
+     }
+     
+     return(list(
+         chain = chain,
+         reward = unlist(reward_sequence),
+         discounted_reward = unlist(discounted_rewards),
+         total_reward = sum(unlist(reward_sequence)),
+         total_discounted_reward = sum(unlist(discounted_rewards))
+     ))
+ }

设置模拟参数

> initial_state <- "s1"    # 初始状态
> n_steps <- 100           # 步长
> gamma <- 0.9             # 折扣因子

# 奖励规则
> rewards<-data.frame("s1"=-1,"s2"=-2,"s3"=-2,"s4"=10,"s5"=1,"s6"=0)

运行带奖励的马尔科夫链函数，

> result <- simulate_markov_reward(p, rewards, initial_state, n_steps, gamma)
 
# 总奖励
> result$total_reward
[1] -23

# 总折现奖励
> result$total_discounted_reward
[1] -9.48585606660266

查看完整和运行结果

> result
$chain          # 马尔科夫链过程
  [1] "s1" "s1" "s1" "s1" "s1" "s1" "s1" "s1" "s1" "s1" "s1"
 [12] "s1" "s1" "s1" "s2" "s1" "s1" "s1" "s1" "s1" "s1" "s1"
 [23] "s1" "s2" "s1" "s1" "s1" "s2" "s3" "s4" "s6" "s6" "s6"
 [34] "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6"
 [45] "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6"
 [56] "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6"
 [67] "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6"
 [78] "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6"
 [89] "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6" "s6"
[100] "s6" "s6"

$reward        # 各个步骤的奖励值
  [1] -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -2 -1 -1 -1
 [19] -1 -1 -1 -1 -1 -2 -1 -1 -1 -2 -2 10  0  0  0  0  0  0
 [37]  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 [55]  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 [73]  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0  0
 [91]  0  0  0  0  0  0  0  0  0  0  0

$discounted_reward   # 各个步骤的折现奖励值
  [1] -1.00000000 -0.90000000 -0.81000000 -0.72900000
  [5] -0.65610000 -0.59049000 -0.53144100 -0.47829690
  [9] -0.43046721 -0.38742049 -0.34867844 -0.31381060
 [13] -0.28242954 -0.25418658 -0.45753585 -0.20589113
 [17] -0.18530202 -0.16677182 -0.15009464 -0.13508517
 [21] -0.12157665 -0.10941899 -0.09847709 -0.17725876
 [25] -0.07976644 -0.07178980 -0.06461082 -0.11629947
 [29] -0.10466953  0.47101287  0.00000000  0.00000000
 [33]  0.00000000  0.00000000  0.00000000  0.00000000
 [37]  0.00000000  0.00000000  0.00000000  0.00000000
 [41]  0.00000000  0.00000000  0.00000000  0.00000000
 [45]  0.00000000  0.00000000  0.00000000  0.00000000
 [49]  0.00000000  0.00000000  0.00000000  0.00000000
 [53]  0.00000000  0.00000000  0.00000000  0.00000000
 [57]  0.00000000  0.00000000  0.00000000  0.00000000
 [61]  0.00000000  0.00000000  0.00000000  0.00000000
 [65]  0.00000000  0.00000000  0.00000000  0.00000000
 [69]  0.00000000  0.00000000  0.00000000  0.00000000
 [73]  0.00000000  0.00000000  0.00000000  0.00000000
 [77]  0.00000000  0.00000000  0.00000000  0.00000000
 [81]  0.00000000  0.00000000  0.00000000  0.00000000
 [85]  0.00000000  0.00000000  0.00000000  0.00000000
 [89]  0.00000000  0.00000000  0.00000000  0.00000000
 [93]  0.00000000  0.00000000  0.00000000  0.00000000
 [97]  0.00000000  0.00000000  0.00000000  0.00000000
[101]  0.00000000

$total_reward   # 总奖励
[1] -23

$total_discounted_reward    # 总折现奖励
[1] -9.485856

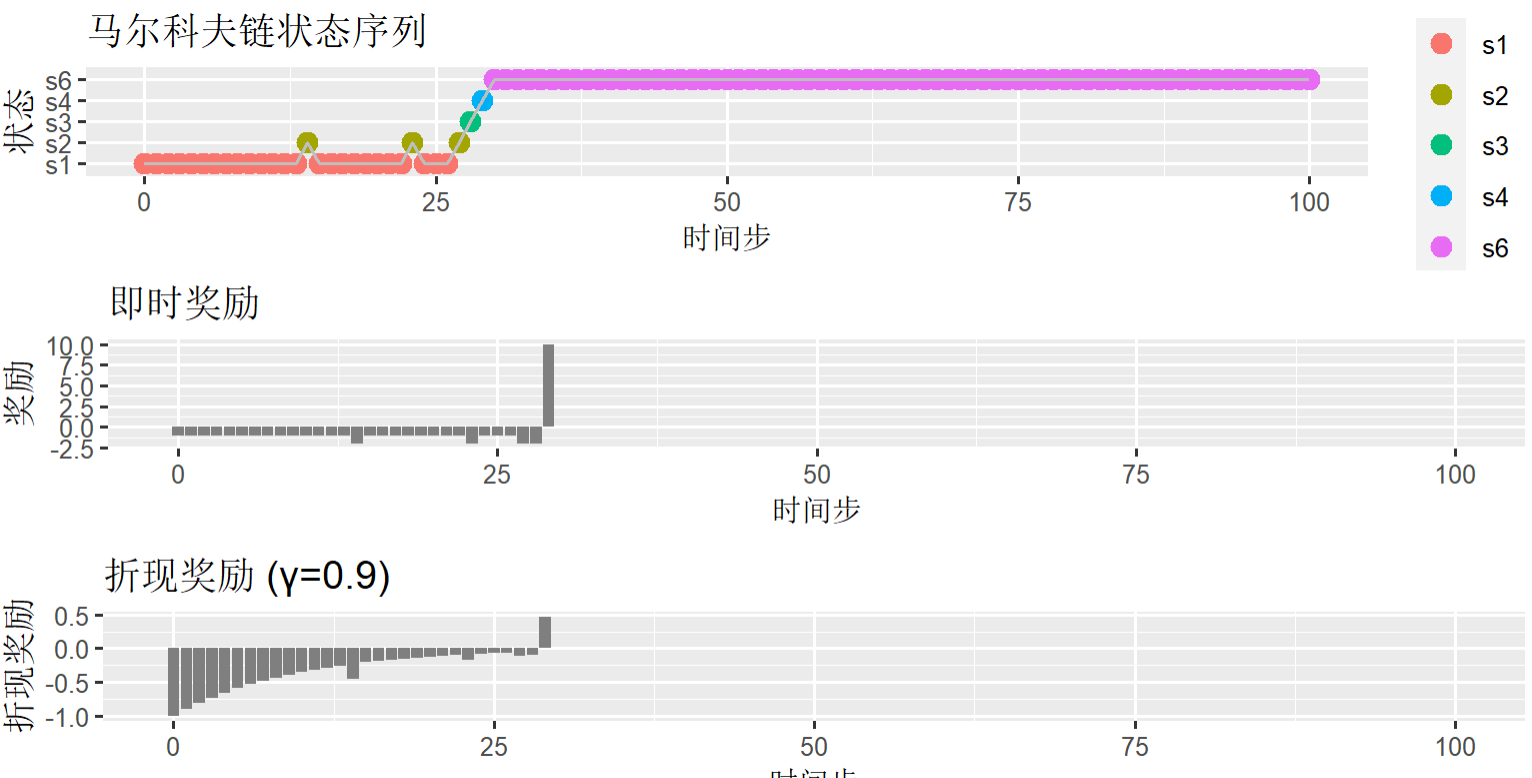
可视化马尔科夫链状态序列，以上面带奖励的马尔科夫链生成的数据集result为基础。

> library(ggplot2)
> library(gridExtra)
 
> # 准备数据
> sim_data <- data.frame(
+     step = 0:n_steps,
+     state = factor(result$chain, levels = s),
+     reward = result$reward,
+     discounted_reward = result$discounted_reward
+ )

> # 绘制马尔科夫链状态序列状态
> p1 <- ggplot(sim_data, aes(x = step, y = state, color = state)) +
+     geom_point(size = 3) +
+     geom_line(aes(group = 1), color = "gray") +
+     labs(title = "马尔科夫链状态序列", x = "时间步", y = "状态")

# 绘制马尔科夫链状态序列奖励
> p2 <- ggplot(sim_data, aes(x = step, y = reward)) +
+     geom_col(aes(fill = state)) +
+     scale_fill_manual(values = c("Sunny" = "gold", "Cloudy" = "gray", "Rainy" = "blue")) +
+     labs(title = "即时奖励", x = "时间步", y = "奖励")

# 绘制马尔科夫链状态序列折现奖励 
> p3 <- ggplot(sim_data, aes(x = step, y = discounted_reward)) +
+     geom_col(aes(fill = state)) +
+     scale_fill_manual(values = c("Sunny" = "gold", "Cloudy" = "gray", "Rainy" = "blue")) +
+     labs(title = paste0("折现奖励 (γ=", gamma, ")"), x = "时间步", y = "折现奖励")
> 
> # 组合图形
> grid.arrange(p1, p2, p3, ncol = 1)

价值函数计算，通过解析解法，直接求解Bellman方程得到精确解。

# 计算状态价值函数
> calculate_state_values <- function(transition_matrix, rewards, gamma = 0.9, epsilon = 1e-6) {
+     n_states <- nrow(transition_matrix)
+     I <- diag(n_states)
+     
+     # 构建线性方程组: V = R + γPV → (I - γP)V = R
+     A <- I - gamma * transition_matrix
+     b <- rewards
+     
+     # 解线性方程组
+     V <- solve(A, b)
+     
+     return(V)
+ }

查看参数

> p
    s1  s2  s3  s4  s5  s6
s1 0.9 0.1 0.0 0.0 0.0 0.0
s2 0.5 0.0 0.5 0.0 0.0 0.0
s3 0.0 0.0 0.0 0.6 0.0 0.4
s4 0.0 0.0 0.0 0.0 0.3 0.7
s5 0.0 0.2 0.3 0.5 0.0 0.0
s6 0.0 0.0 0.0 0.0 0.0 1.0

> rewards
  s1 s2 s3 s4 s5 s6
1 -1 -2 -2 10  1  0

> gamma<-0.5
> gamma
[1] 0.5

计算状态价值

> state_values <- calculate_state_values(p, rewards, gamma)
> state_values
       s1        s2        s3        s4        s5        s6 
-2.019502 -2.214518  1.161428 10.538093  3.587286  0.000000 

本文初步探索了，马尔科夫决策过程中的基本概念，包括奖励过程、价值函数和策略优化。通过调整折扣因子γ、奖励值或转移矩阵来观察这些变化如何影响最优策略和价值函数。

本文的代码已上传到github:https://github.com/bsspirit/ml/blob/master/mavkov.r

本文有部分代码是通过Deepseek生成，再次惊叹Deepseek的强大。

转载请注明出处：
http://blog.fens.me/r-markov/