R的极客理想系列文章,涵盖了R的思想,使用,工具,创新等的一系列要点,以我个人的学习和体验去诠释R的强大。
R语言作为统计学一门语言,一直在小众领域闪耀着光芒。直到大数据的爆发,R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入,R语言的社区在迅速扩大成长。现在已不仅仅是统计领域,教育,银行,电商,互联网….都在使用R语言。
要成为有理想的极客,我们不能停留在语法上,要掌握牢固的数学,概率,统计知识,同时还要有创新精神,把R语言发挥到各个领域。让我们一起动起来吧,开始R的极客理想。
关于作者:
- 张丹,分析师/程序员/Quant: R,Java,Nodejs
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-markdown-math-latex/
前言
我们编写专业的学术文档时,一定会有数学公式的部分。那么如何在rmarkdown的文档中,加入数学公式呢?这其实并不难,需要了解laTex语法结构,再多练练。然后使用时,知道去哪里查就行了。有点像使用正则表达式,随写随查。
目录
- 在rmarkdown文档中加入数学公式
- laTex 数学公式语法
- 用R来完成作业
1. 在rmarkdown文档中加入数学公式
我们在写专业的论文时,经常需要加入数学公式,我们在利用 rmarkdown 来写文档时,可以支持加入数学公式。rmarkdown是一个R语言支持的写文档的方便工具,RStudio工具已经有了集成支持,在 用R编写markdown格式文档 一文中,我详细地介绍的 rmarkdown 文档的写法。
在了解了 rmarkdown 文档的使用后,本文将介绍在文档中加入 laTex语法的数学公式,来进行数学公式的编辑。
在插入数学公式时,有2种语法,用 $ 和 $$ 的。
- 行内公式:将公式插入到本行内,符号:$公式内容$,如:$xyz$,
- 多行公式:将公式插入到新的一行内,并且居中,符号:$$公式内容$$。
2. laTex 数学公式语法
在我们使用公式时,需要了解laTex的数学公式的语法,正确使用公式语法,才能正确输出想要的公式结果,公式语法分为几大类分别进行介绍。
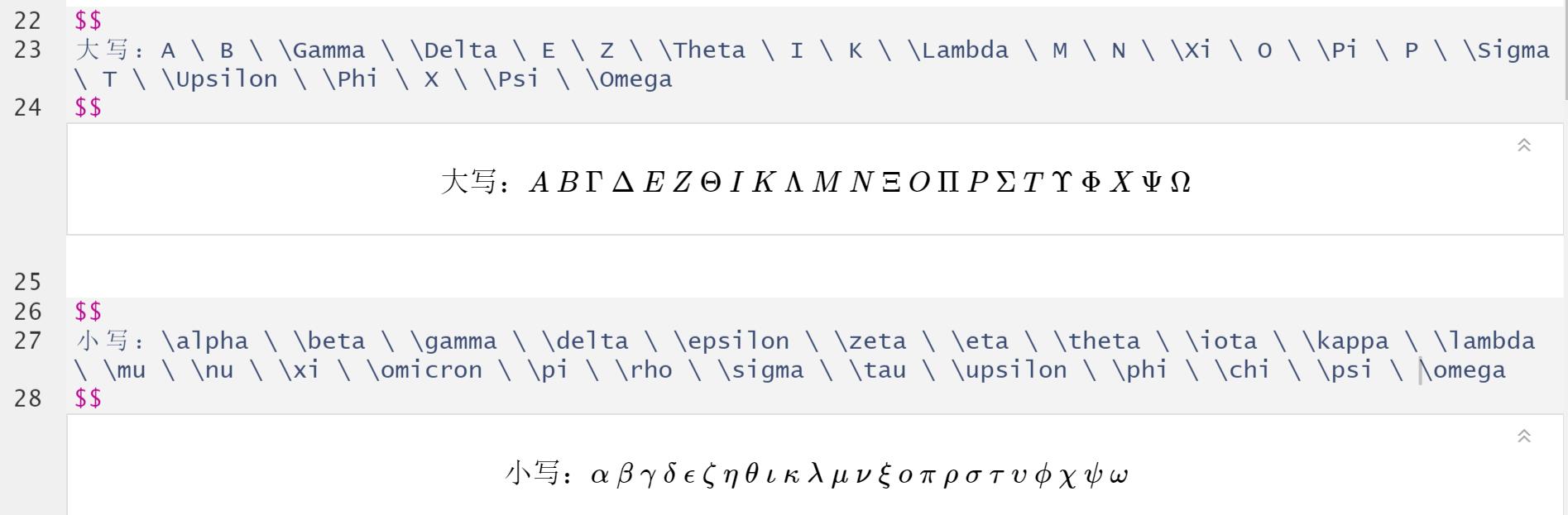
2.1 希腊字母表
| 名称 | 大写 | code | 小写 | code |
|---|---|---|---|---|
| alpha | A | A | α | \alpha |
| beta | B | B | β | \beta |
| gamma | Γ | \Gamma | γ | \gamma |
| delta | Δ | \Delta | δ | \delta |
| epsilon | E | E | ϵ | \epsilon |
| zeta | Z | Z | ζ | \zeta |
| eta | H | H | η | \eta |
| theta | Θ | \Theta | θ | \theta |
| iota | I | I | ι | \iota |
| kappa | K | K | κ | \kappa |
| lambda | Λ | \Lambda | λ | \lambda |
| mu | M | M | μ | \mu |
| nu | N | N | ν | \nu |
| xi | Ξ | \Xi | ξ | \xi |
| omicron | O | O | ο | \omicron |
| pi | Π | \Pi | π | \pi |
| rho | P | P | ρ | \rho |
| sigma | Σ | \Sigma | σ | \sigma |
| tau | T | T | τ | \tau |
| upsilon | Υ | \Upsilon | υ | \upsilon |
| phi | Φ | \Phi | ϕ | \phi |
| chi | X | X | χ | \chi |
| psi | Ψ | \Psi | ψ | \psi |
| omega | Ω | \Omega | ω | \omega |
2.2 四则运算
| 符号名 | 代码 | 实例 |
|---|---|---|
| 加号 | + | a+b |
| 减号 | – | a-b |
| 加减号 | \pm | a \pm b |
| 减加号 | \mp | a \mp b |
| 乘号 | \times | a \times b |
| 星乘 | – | a-b |
| 点乘 | \cdot | a \cdot b |
| 除号 | \div | a \div b |
| 斜除 | / | a / b |
2.3 括号
1、小括号与方括号
使用原始的( )、[ ],如(2+3)*[4+4]。
2、大括号
由于大括号{}被用来分组,需要使用\{和\}表示大括号,或者可以使用\lbrace 和\rbrace来表示。如\{a*b\} 或 \lbrace a*b \rbrace
3、尖括号
使用\langle和\rangle表示左尖括号和右尖括号。如\langle x \rangle。
4、上取整和下取整
使用\lceil 和 \rceil 表示上取整,如\lceil x \rceil。使用\lfloor 和 \rfloor 表示下取整,如\lfloor x \rfloor
2.4 上标、下标、顶部
上标使用^,下标使用_,例如x_i^2
默认情况下,上下标符号仅仅对下一个组起作用。一个组即单个字符或者使用{..}包裹起来的内容,对比10^10不同于10^{10}。使用大括号可以消除二义性 ,如x^5^6是错误的语法,需要写成 {x^5}^6 或者 x^{5^6}。

2.5 求和,积分,连乘、交集并集、最大最小、自变量集
本分类的都可以使用类似语法加下限和上限,下限用_,上限用^,如\sum_{i=1}^n。
求和:使用 \sum,下限用_,上限用^,如\sum_{i=1}^n
积分:使用\int,下限用_,上限用^,如\int{i=1}^\infty
多重积分:使用\int, \iint, \iiint
连乘: 使用\prod,下限用_,上限用^,如\int{i=1}^n
交集和并集:使用\bigcpu和\bigcap
最大和最小:使用\max 和 \min
最大最小自变量集:使用\mathop {argmax}_{c_k} 和 \mathop {argmin}_{c_k}。
2.6 分式、连分式、根式
分式有2种语法:第一种是使用/frac,如/frac ab,其中a为分子,b为分母。第二种是使用\over,如 {a+b\over c+d},其中\over之前为分子,之后为分母。
连分式:可以直接使用/frac的分式的写法,也可以用/cfrac语法,这种方法字体不缩小。
根式:使用\sqrt,默认为平方根,如\sqrt[4]{a+b},[4]为几次方根,{a+b}为具体的值。
2.7 分类表达式、多行表达式、方程组、占位符
分类表达式:使用\begin{cases}…\end{cases} 的语法。
多行表达式:使用begin{equation}...end{equation}的语法;使用begin{split}表示开始多行公式,end{split}表示结束。
方程组:使用\begin{array}...\end{array}与\left \{与\right.配合表示方程组,也可以使用\begin{cases}…\end{cases}表示。
占位符:换行 \\,多位换行\\[3ex] 3ex可以改成5ex等, 较大间隙空格\; , 普通空格\ ,更大间隙空格\quad 与 \qquad,对齐&。
2.8 三角函数,反三角函数
三角函数:正弦\sin,余弦\cos,正切\tan x,余切\cot x , 正割\sec x ,余割\csc x
反三角函数:反正弦\sin,反余弦\cos,反正切\tan x
2.9 运算符,排列组合,求模
比较运算符:小于\lt,大于 \gt ,小于等于 \le ,大于等于 \ge ,不等于\ne ,不\not ,不小于 \not\lt
集合运算符:求并集\cup,求交集 \cap,求差集\setminus,子集\subset,在子集 \subseteq ,不在子集 \subsetneq,父集\supset,属于\in,不属于\notin,空集 \emptyset,空\varnothing
对数运算符:使用\log ,\lg,\ln,如\log_2 10,其中2为底,b为值。
排列组合:使用\binom或者\choose
模运算:使用\pmod
2.10 特殊符号
特征符号,包括箭头,逻辑运算符,符号,多种等于,范围类型,点类型,顶部标记,连线符号。
2.11 表格
\begin{array}{列样式}…\end{array} 这样的形式来创建表格,列样式可以是clr 表示居中,左,右对齐,使用| 表示一条竖线。表格中各行使用\\ 分隔,各列使用& 分隔。使用\hline 在本行前加入一条直线。2.12 矩阵
普通矩阵:使用\begin{matrix}…\end{matrix} 表示矩阵。
矩阵扩号:对矩阵加括号对应有不同的类型,小括号{pmatrix},中括号{bmatrix},大括号{Bmatrix},竖线{vmatrix},双竖线{Vmatrix}。
省略元素矩阵:使用省略号与普通矩阵进行组合 \cdots,\ddots,\vdots
增广矩阵:使用表格中使用到的\begin{array} ... \end{array} 来实现。
2.13 标记与引用
bbbb
2.14 字体
| 符号名 | 代码 |
|---|---|
| 黑板粗体字 | \mathbb,\Bbb |
| 黑体字 | \mathbf,\bf |
| 打印机字体 | \mathtt,\tt |
| 罗马字体 | \mathrm,\rm |
| 手写字体 | \mathscr |
| Fraktur字母 | \mathfrak |
| 意大利体 | \it |
| 花体 | \cal |
| 等斜体 | \sf |
| 数字斜体 | \mit |
2.15 颜色
| 符号名 | 代码 |
|---|---|
| 黑色 | \color{black} |
| 灰色 | \color{gray} |
| 银色 | \color{silver} |
| 白色 | \color{white} |
| 栗色 | \color{maroon} |
| 红色 | \color{red} |
| 黄色 | \color{yellow} |
| 青柠色 | \color{lime} |
| 橄榄色 | \color{olive} |
| 绿色 | \color{green} |
| 绿色 | \color{green} |
| 鸭绿色 | \color{teal} |
| 青色 | \color{aqua} |
| 蓝色 | \color{blue} |
| 海军蓝 | \color{navy} |
| 紫色 | \color{purple} |
| 紫红色 | \color{fuchsia} |
3. 用R来完成作业
下面我找2道国外留学朋友遇到的作业题,来看一下,怎么用rmarkdown来完成作业的要求。
1. Show that the OLS estimator for β1 in the simple linear regression model can be written as.

代码
\hat\beta_1=\frac{\sum\left(X_i-\overline{X}\right)Y_i}{\sum\left(X_i-\overline{X}\right)^2}=\frac{\sum X_iY_i-\overline{X}\sum Y_i}{\sum X_i^2+\sum \overline{X}^2 - 2\overline{X}\sum X_i}\\
=\frac{\sum X_iY_i-\overline{X}*N\overline{Y}}{\sum X_i^2+N\overline{X}^2 - 2\overline{X}*N\overline{X}}
=\frac{\sum^{N}_{i=1} X_iY_i-N\overline{XY}}{\sum^{N}_{i=1}Xi^2-N\overline{X}^2}
2a.Find the OLS estimator for β1 in the linear regression model with no intercept term, i.e., in the regression Yi=β1Xi+Ei, i=1,2,...,N. Which algebraic properties of OLS estimatios discussed in the notes continue to hold and which are lost? Will the R^2 still necessarily lie between 0 and 1?
代码
SSR=\sum^{N}_{i=1}\hat E_i^2 = \sum\left(Y_i-\hat\beta_1X_i\right)^2\\
FOC:\frac{\partial SSR}{\partial Xi} = -2 \sum\left(Y_i-\hat\beta_1X_i\right)\hat\beta_1= -2\hat\beta_1\sum\left(Y_i-\hat\beta_1X_i\right)=0\\
=>\sum^{N}_{i=1}\hat E_i=\sum\left(Y_i-\hat\beta_1X_i\right)=0\\
\frac{\partial SSR}{\partial \beta_1}=-2\sum\left(Y_i-\hat\beta_1X_i\right)X_i=0\\
=> \sum^{N}_{i=1}X_i\hat E_i=\sum X_i\left(Y_i-\hat\beta_1X_i\right)=0
2b. What is the OLS estimator for β0 in the linear regression model with no regressor, i.e., in the regression Yi=β0 + Ei? What is the R^2 for this regression? Remark :All of regressions will include the intercept term, unless explicitly stated otherwise.
代码
SSR=\sum^{N}_{i=1}E_i^2=\sum\left(Y_i-\beta_0\right)^2\\
\frac{\partial SSR}{\partial\hat\beta_0}|_{\hat\beta_0^{ols}} =-2\sum^{N}_{i=1}\left(Y_i-\beta_0\right)=-2N\overline{Y}+2N\beta_0=0 => \hat\beta_0=\overline{Y}\\
=>SST=\sum^{N}_{i=1}\left(Y_i-\overline{Y}\right)^2=\sum\left(\overline{Y}+\hat E_i-\overline{Y}\right)^2=\sum\hat E_i^2\\
=> R^2=1-\frac{SSR}{SST}=0
有了数学公式的编写神器,感觉完成作业简直太顺手了。只是用数学公式进行解题和推理,对我来说真是太难了。我还是喜欢写程序。哈哈哈!
转载请注明出处:
http://blog.fens.me/r-markdown-math-latex/