R的极客理想系列文章,涵盖了R的思想,使用,工具,创新等的一系列要点,以我个人的学习和体验去诠释R的强大。
R语言作为统计学一门语言,一直在小众领域闪耀着光芒。直到大数据的爆发,R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入,R语言的社区在迅速扩大成长。现在已不仅仅是统计领域,教育,银行,电商,互联网….都在使用R语言。
要成为有理想的极客,我们不能停留在语法上,要掌握牢固的数学,概率,统计知识,同时还要有创新精神,把R语言发挥到各个领域。让我们一起动起来吧,开始R的极客理想。
关于作者:
- 张丹(Conan), 程序员Java,R,PHP,Javascript
- weibo:@Conan_Z
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-mathematics/
前言
R是作为统计语言,生来就对数学有良好的支持,一个函数就能实现一种数学计算,所以用R语言做数学计算题特别方便。如果计算器中能嵌入R的计算函数,那么绝对是一种高科技产品。
本文总结了R语言用于初等数学中的各种计算。
目录
- 基本计算
- 三角函数计算
- 复数计算
- 方程计算
1 基本计算
四则运算: 加减乘除, 余数, 整除, 绝对值, 判断正负
> a<-10;b<-5
# 加减乘除
> a+b;a-b;a*b;a/b
[1] 15
[1] 5
[1] 50
[1] 2
# 余数,整除
> a%%b;a%/%b
[1] 0
[1] 2
# 绝对值
> abs(-a)
[1] 10
# 判断正负
> sign(-2:3)
[1] -1 -1 0 1 1 1
数学计算: 幂, 自然常用e的幂, 平方根, 对数
> a<-10;b<-5;c<-4
# 幂
> c^b;c^-b;c^(b/10)
[1] 1024
[1] 0.0009765625
[1] 2
# 自然常数e
> exp(1)
[1] 2.718282
# 自然常数e的幂
> exp(3)
[1] 20.08554
# 平方根
> sqrt(c)
[1] 2
# 以2为底的对数
> log2(c)
[1] 2
# 以10为底的对数
> log10(b)
[1] 0.69897
# 自定义底的对数
> log(c,base = 2)
[1] 2
# 自然常数e的对数
> log(a,base=exp(1))
[1] 2.302585
# 指数对数操作
> log(a^b,base=a)
[1] 5
> log(exp(3))
[1] 3
比较计算: ==, >, <, !=, <=, >=, isTRUE, identical
> a<-10;b<-5
# 比较计算
> a==a;a!=b;a>b;a=c
[1] TRUE
[1] TRUE
[1] TRUE
[1] FALSE
[1] FALSE
[1] TRUE
# 判断是否为TRUE
> isTRUE(a)
[1] FALSE
> isTRUE(!a)
[1] FALSE
# 精确比较两个对象
> identical(1, as.integer(1))
[1] FALSE
> identical(NaN, -NaN)
[1] TRUE
> f <- function(x) x
> g <- compiler::cmpfun(f)
> identical(f, g)
[1] TRUE
逻辑计算: &, |, &&, ||, xor
> x<-c(0,1,0,1)
> y<-c(0,0,1,1)
# 只比较第一个元素 &&, ||
> x && y;x || y
[1] FALSE
[1] FALSE
# S4对象的逻辑运算,比较所有元素 &, |
> x & y;x | y
[1] FALSE FALSE FALSE TRUE
[1] FALSE TRUE TRUE TRUE
# 异或
> xor(x,y)
[1] FALSE TRUE TRUE FALSE
> xor(x,!y)
[1] TRUE FALSE FALSE TRUE
约数计算: ceiling,floor,trunc,round,signif
# 向上取整
> ceiling(5.4)
[1] 6
# 向下取整
> floor(5.8)
[1] 5
# 取整数
> trunc(3.9)
[1] 3
# 四舍五入
> round(5.8)
# 四舍五入,保留2位小数
> round(5.8833, 2)
[1] 5.88
# 四舍五入,保留前2位整数
> signif(5990000,2)
[1] 6e+06
数组计算: 最大, 最小, 范围, 求和, 均值, 加权平均, 连乘, 差分, 秩,,中位数, 分位数, 任意数,全体数
> d<-seq(1,10,2);d
[1] 1 3 5 7 9
# 求最大值,最小值,范围range
> max(d);min(d);range(d)
[1] 9
[1] 1
[1] 1 9
# 求和,均值
> sum(d),mean(d)
[1] 25
[1] 5
# 加权平均
> weighted.mean(d,rep(1,5))
[1] 5
> weighted.mean(d,c(1,1,2,2,2))
[1] 5.75
# 连乘
> prod(1:5)
[1] 120
# 差分
> diff(d)
[1] 2 2 2 2
# 秩
> rank(d)
[1] 1 2 3 4 5
# 中位数
> median(d)
[1] 5
# 分位数
> quantile(d)
0% 25% 50% 75% 100%
1 3 5 7 9
# 任意any,全体all
> e<-seq(-3,3);e
[1] -3 -2 -1 0 1 2 3
> any(e<0);all(e<0)
[1] TRUE
[1] FALSE
排列组合计算: 阶乘, 组合, 排列
# 5!阶乘
> factorial(5)
[1] 120
# 组合, 从5个中选出2个
> choose(5, 2)
[1] 10
# 列出从5个中选出2个的组合所有项
> combn(5,2)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 1 1 1 1 2 2 2 3 3 4
[2,] 2 3 4 5 3 4 5 4 5 5
# 计算0:10的组合个数
> for (n in 0:10) print(choose(n, k = 0:n))
[1] 1
[1] 1 1
[1] 1 2 1
[1] 1 3 3 1
[1] 1 4 6 4 1
[1] 1 5 10 10 5 1
[1] 1 6 15 20 15 6 1
[1] 1 7 21 35 35 21 7 1
[1] 1 8 28 56 70 56 28 8 1
[1] 1 9 36 84 126 126 84 36 9 1
[1] 1 10 45 120 210 252 210 120 45 10 1
# 排列,从5个中选出2个
> choose(5, 2)*factorial(2)
[1] 20
累积计算: 累加, 累乘, 最小累积, 最大累积
# 累加
> cumsum(1:5)
[1] 1 3 6 10 15
# 累乘
> cumprod(1:5)
[1] 1 2 6 24 120
> e<-seq(-3,3);e
[1] -3 -2 -1 0 1 2 3
# 最小累积cummin
> cummin(e)
[1] -3 -3 -3 -3 -3 -3 -3
# 最大累积cummax
> cummax(e)
[1] -3 -2 -1 0 1 2 3
两个数组计算: 交集, 并集, 差集, 数组是否相等, 取唯一, 查匹配元素的索引, 找重复元素索引
# 定义两个数组向量
> x <- c(9:20, 1:5, 3:7, 0:8);x
[1] 9 10 11 12 13 14 15 16 17 18 19 20 1 2 3 4 5
[18] 3 4 5 6 7 0 1 2 3 4 5 6 7 8
> y<- 1:10;y
[1] 1 2 3 4 5 6 7 8 9 10
# 交集
> intersect(x,y)
[1] 9 10 1 2 3 4 5 6 7 8
# 并集
> union(x,y)
[1] 9 10 11 12 13 14 15 16 17 18 19 20 1 2 3 4 5
[18] 6 7 0 8
# 差集,从x中排除y
> setdiff(x,y)
[1] 11 12 13 14 15 16 17 18 19 20 0
# 判断是否相等
> setequal(x, y)
[1] FALSE
# 取唯一
> unique(c(x,y))
[1] 9 10 11 12 13 14 15 16 17 18 19 20 1 2 3 4 5
[18] 6 7 0 8
# 找到x在y中存在的元素的索引
> which(x %in% y)
[1] 1 2 13 14 15 16 17 18 19 20 21 22 24 25 26 27 28
[18] 29 30 31
> which(is.element(x,y))
[1] 1 2 13 14 15 16 17 18 19 20 21 22 24 25 26 27 28
[18] 29 30 31
# 找到重复元素的索引
> which(duplicated(x))
[1] 18 19 20 24 25 26 27 28 29 30
2 三角函数计算
2.1 三角函数
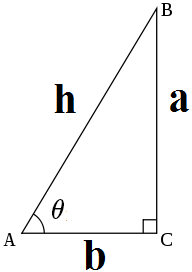
在直角三角形中仅有锐角(大小在0到90度之间的角)三角函数的定义。给定一个锐角θ,可以做出一个直角三角形,使得其中的一个内角是θ。设这个三角形中,θ的对边、邻边和斜边长度分别是a、b和h。
三角函数的6种关系:正弦,余弦,正切,余切,正割,余割。
- θ的正弦是对边与斜边的比值:sin θ = a/h
- θ的余弦是邻边与斜边的比值:cos θ = b/h
- θ的正切是对边与邻边的比值:tan θ = a/b
- θ的余切是邻边与对边的比值:cot θ = b/a
- θ的正割是斜边与邻边的比值:sec θ = h/b
- θ的余割是斜边与对边的比值:csc θ = h/a
三角函数的特殊值:
函数 0 pi/12 pi/6 pi/4 pi/3 5/(12*pi) pi/2
sin 0 (sqrt(6)-sqrt(2))/4 1/2 sqrt(2)/2 sqrt(3)/2 (sqrt(6)+sqrt(2))/4 1
cos 1 (sqrt(6)+sqrt(2))/4 sqrt(3)/2 sqrt(2)/2 1/2 (sqrt(6)-sqrt(2))/4 0
tan 0 2-sqrt(3) sqrt(3)/3 1 sqrt(3) 2+sqrt(3) NA
cot NA 2+sqrt(3) sqrt(3) 1 sqrt(3)/3 2-sqrt(3) 0
sec 1 sqrt(6)-sqrt(2) sqrt(3)*2/3 sqrt(2) 2 sqrt(6)-sqrt(2) NA
csc NA 2 sqrt(2) sqrt(3)*2/3 sqrt(6)-sqrt(2) 1 NA
三角基本函数: 正弦,余弦,正切
# 正弦
> sin(0);sin(1);sin(pi/2)
[1] 0
[1] 0.841471
[1] 1
# 余弦
> cos(0);cos(1);cos(pi)
[1] 1
[1] 0.5403023
[1] -1
# 正切
> tan(0);tan(1);tan(pi)
[1] 0
[1] 1.557408
[1] -1.224647e-16
接下来,我们用ggplot2包来画出三角函数的图形。
# 加载ggplot2的库
> library(ggplot2)
> library(scales)
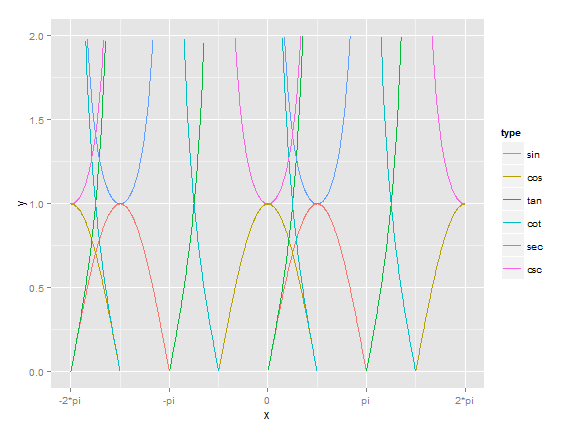
三角函数画图
# x坐标
> x<-seq(-2*pi,2*pi,by=0.01)
# y坐标
> s1<-data.frame(x,y=sin(x),type=rep('sin',length(x)))# 正弦
> s2<-data.frame(x,y=cos(x),type=rep('cos',length(x)))# 余弦
> s3<-data.frame(x,y=tan(x),type=rep('tan',length(x)))# 正切
> s4<-data.frame(x,y=1/tan(x),type=rep('cot',length(x)))# 余切
> s5<-data.frame(x,y=1/sin(x),type=rep('sec',length(x)))# 正割
> s6<-data.frame(x,y=1/cos(x),type=rep('csc',length(x)))# 余割
> df<-rbind(s1,s2,s3,s4,s5,s6)
# 用ggplot2画图
> g<-ggplot(df,aes(x,y))
> g<-g+geom_line(aes(colour=type,stat='identity'))
> g<-g+scale_y_continuous(limits=c(0, 2))
> g<-g+scale_x_continuous(breaks=seq(-2*pi,2*pi,by=pi),labels=c("-2*pi","-pi","0","pi","2*pi"))
> g
2.1 反三角函数
基本的反三角函数定义:
反三角函数 定义 值域
arcsin(x) = y sin(y) = x - pi/2 <= y <= pi/2
arccos(x) = y cos(y) = x 0 <= y <= pi,
arctan(x) = y tan(y) = x - pi/2 < y < pi/2
arccsc(x) = y csc(y) = x - pi/2 <= y <= pi/2, y!=0
arcsec(x) = y sec(y) = x 0 <= y <= pi, y!=pi/2
arccot(x) = y cot(y) = x 0 < y < pi
反正弦,反余弦,反正切
# 反正弦asin
> asin(0);asin(1)
[1] 0
[1] 1.570796 # pi/2=1.570796
# 反余弦acos
> acos(0);acos(1)
[1] 1.570796 # pi/2=1.570796
[1] 0
# 反正切atan
> atan(0);atan(1)
[1] 0
[1] 0.7853982 # pi/4=0.7853982
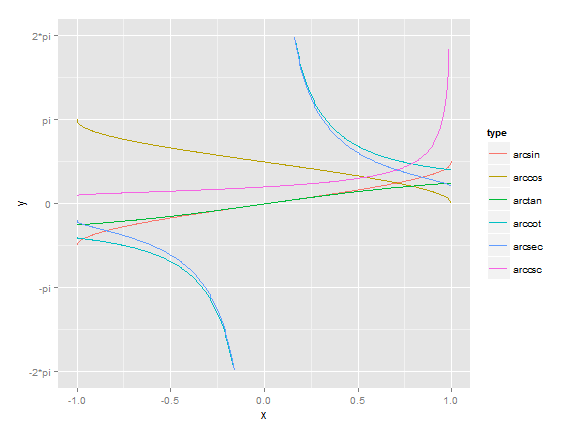
反三角函数画图
# x坐标
> x<-seq(-1,1,by=0.005)
# y坐标
> s1<-data.frame(x,y=asin(x),type=rep('arcsin',length(x)))
> s2<-data.frame(x,y=acos(x),type=rep('arccos',length(x)))
> s3<-data.frame(x,y=atan(x),type=rep('arctan',length(x)))
> s4<-data.frame(x,y=1/atan(x),type=rep('arccot',length(x)))
> s5<-data.frame(x,y=1/asin(x),type=rep('arcsec',length(x)))
> s6<-data.frame(x,y=1/acos(x),type=rep('arccsc',length(x)))
> df<-rbind(s1,s2,s3,s4,s5,s6)
# 用ggplot2画图
> g<-ggplot(df,aes(x,y))
> g<-g+geom_line(aes(colour=type,stat='identity'))
> g<-g+scale_y_continuous(limits=c(-2*pi,2*pi),breaks=seq(-2*pi,2*pi,by=pi),labels=c("-2*pi","-pi","0","pi","2*pi"))
> g
2.3 三角函数公式
接下来,用单元测试的方式,来描述三角函数的数学公式。通过testthat包,进行单元测试,关于testthat包的安装和使用,请参考文章:在巨人的肩膀前行 催化R包开发
# 加载testthat包
> library(testthat)
# 定义变量
> a<-5;b<-10
平方和公式:
- sin(x)^2+cos(x)^2 = 1
expect_that(sin(a)^2+cos(a)^2,equals(1))
和角公式
- sin(a+b) = sin(a)*cos(b)+sin(b)*cos(a)
- sin(a-b) = sin(a)*cos(b)-sin(b)*cos(a)
- cos(a+b) = cos(a)*cos(b)-sin(b)*sin(a)
- cos(a-b) = cos(a)*cos(b)+sin(b)*sin(a)
- tan(a+b) = (tan(a)+tan(b))/(1-tan(a)*tan(b))
- tan(a-b) = (tan(a)-tan(b))/(1+tan(a)*tan(b))
expect_that(sin(a)*cos(b)+sin(b)*cos(a),equals(sin(a+b)))
expect_that(sin(a)*cos(b)-sin(b)*cos(a),equals(sin(a-b)))
expect_that(cos(a)*cos(b)-sin(b)*sin(a),equals(cos(a+b)))
expect_that(cos(a)*cos(b)+sin(b)*sin(a),equals(cos(a-b)))
expect_that((tan(a)+tan(b))/(1-tan(a)*tan(b)),equals(tan(a+b)))
expect_that((tan(a)-tan(b))/(1+tan(a)*tan(b)),equals(tan(a-b)))
2倍角公式
- sin(2*a) = 2*sin(a)*cos(a)
- cos(2*a) = cos(a)^2-sin(a)^2=2*cos(a)^2-1=1-2*sin2(a)
expect_that(cos(a)^2-sin(a)^2,equals(cos(2*a)))
expect_that(2*cos(a)^2-1,equals(cos(2*a)))
expect_that(1-2*sin(a)^2,equals(cos(2*a)))
3倍角公式
- cos(3*a) = 4*cos(a)^3-3*cos(a)
- sin(3*a) = -4*sin(a)^3+3*sin(a)
expect_that(4*cos(a)^3-3*cos(a),equals(cos(3*a)))
expect_that(-4*sin(a)^3+3*sin(a),equals(sin(3*a)))
半角公式
- sin(a/2) = sqrt((1-cos(a))/2)
- cos(a/2) = sqrt((1+cos(a))/2)
- tan(a/2) = sqrt((1-cos(a))/(1+cos(a))) = sin(a)/(1+cos(a)) = (1-cos(a))/sin(a)
expect_that(sqrt((1-cos(a))/2),equals(abs(sin(a/2))))
expect_that(sqrt((1+cos(a))/2),equals(abs(cos(a/2))))
expect_that(sqrt((1-cos(a))/(1+cos(a))),equals(abs(tan(a/2))))
expect_that(abs(sin(a)/(1+cos(a))),equals(abs(tan(a/2))))
expect_that(abs((1-cos(a))/sin(a)),equals(abs(tan(a/2))))
和差化积
- sin(a)*cos(b) = (sin(a+b)+sin(a-b))/2
- cos(a)*sin(b) = (sin(a+b)-sin(a-b))/2
- cos(a)*cos(b) = (cos(a+b)+cos(a-b))/2
- sin(a)*sin(b) = (cos(a-b)-cos(a+b))/2
expect_that((sin(a+b)+sin(a-b))/2,equals(sin(a)*cos(b)))
expect_that((sin(a+b)-sin(a-b))/2,equals(cos(a)*sin(b)))
expect_that((cos(a+b)+cos(a-b))/2,equals(cos(a)*cos(b)))
expect_that((cos(a-b)-cos(a+b))/2,equals(sin(a)*sin(b)))
积化和差
- sin(a)+sin(b) = 2*sin((a+b)/2)*cos((a+b)/2)
- sin(a)-sin(b) = 2*cos((a+b)/2)*cos((a-b)/2)
- cos(a)+cos(b) = 2*cos((a+b)/2)*cos((a-b)/2)
- cos(a)-cos(b) = -2*sin((a+b)/2)*sin((a-b)/2)
expect_that(sin(a)+sin(b),equals(2*sin((a+b)/2)*cos((a-b)/2)))
expect_that(sin(a)-sin(b),equals(2*cos((a+b)/2)*sin((a-b)/2)))
expect_that(2*cos((a+b)/2)*cos((a-b)/2),equals(cos(a)+cos(b)))
expect_that(-2*sin((a+b)/2)*sin((a-b)/2),equals(cos(a)-cos(b)))
万能公式
- sin(2*a)=2*tan(a)/(1+tan(a)^2)
- cos(2*a)=(1-tan(a)^2)/(1+tan(a)^2)
- tan(2*a)=2*tan(a)/(1-tan(a)^2)
expect_that(sin(2*a),equals(2*tan(a)/(1+tan(a)^2)))
expect_that((1-tan(a)^2)/(1+tan(a)^2),equals(cos(2*a)))
expect_that(2*tan(a)/(1-tan(a)^2),equals(tan(2*a)))
平方差公式
- sin(a+b)*sin(a-b)=sin(a)^2+sin(b)^2
- cos(a+b)*cos(a-b)=cos(a)^2+sin(b)^2
expect_that(sin(a)^2-sin(b)^2,equals(sin(a+b)*sin(a-b)))
expect_that(cos(a)^2-sin(b)^2,equals(cos(a+b)*cos(a-b)))
降次升角公式
- cos(a)^2=(1+cos(2*a))/2
- sin(a)^2=(1-cos(2*a))/2
expect_that((1+cos(2*a))/2,equals(cos(a)^2))
expect_that((1-cos(2*a))/2,equals(sin(a)^2))
辅助角公式
- a*sin(a)+b*cos(a) = sqrt(a^2+b^2)*sin(a+atan(b/a))
expect_that(sqrt(a^2+b^2)*sin(a+atan(b/a)),equals(a*sin(a)+b*cos(a)))
3 复数计算
复数,为实数的延伸,它使任一多项式都有根。复数中的虚数单位i,是-1的一个平方根,即i^2 = -1。任一复数都可表达为x + yi,其中x及y皆为实数,分别称为复数之“实部”和“虚部”。
3.1 创建一个复数
# 直接创建复数
> ai<-5+2i;ai
[1] 5+2i
> class(ai)
[1] "complex"
# 通过complex()函数创建复数
> bi<-complex(real=5,imaginary=2);bi
[1] 5+2i
> is.complex(bi)
[1] TRUE
# 实数部分
> Re(ai)
[1] 5
# 虚数部分
> Im(ai)
[1] 2
# 取模
> Mod(ai)
[1] 5.385165 # sqrt(5^2+2^2) = 5.385165
# 取辐角
> Arg(ai)
[1] 0.3805064
# 取轭
> Conj(ai)
[1] 5-2i
3.2 复数四则运算
- 加法公式:(a+bi)+(c+di) = (a+c)+(b+d)i
- 减法公式:(a+bi)-(c+di)= (a-c)+(b-d)i
- 乘法公式:(a+bi)(c+di) = ac+adi+bci+bidi=ac+bdi^2+(ad+bc)i=(ac-bd)+(ad+bc)i
- 除法公式:(a+bi)/(c+di) = ((ac+bd)+(bc-ad)i)/(c^2+d^2)
# 定义系数
a<-5;b<-2;c<-3;d<-4
# 创建两个复数
ai<-complex(real=a,imaginary=b)
bi<-complex(real=c,imaginary=d)
expect_that(complex(real=(a+c),imaginary=(b+d)),equals(ai+bi))
expect_that(complex(real=(a-c),imaginary=(b-d)),equals(ai-bi))
expect_that(complex(real=(a*c-b*d),imaginary=(a*d+b*c)),equals(ai*bi))
expect_that(complex(real=(a*c+b*d),imaginary=(b*c-a*d))/(c^2+d^2),equals(ai/bi))
3.3 复数开平方根
# 在实数域,给-9开平方根
> sqrt(-9)
[1] NaN
# 在复数域,给-9开平方根
> sqrt(complex(real=-9))
[1] 0+3i
4 方程计算
方程计算是数学计算的一种基本形式,R语言也可以很方便地帮助我们解方程,下面将介绍一元多次的方程,和二元一次方程的解法。
解一元多次方程,可以用uniroot()函数!
4.1 一元一次方程
一元一次方程:a*x+b=0,设a=5,b=10,求x?
# 定义方程函数
> f1 <- function (x, a, b) a*x+b
# 给a,b常数赋值
> a<-5;b<-10
# 在(-10,10)的区间,精确度为0.0001位,计算方程的根
> result <- uniroot(f1,c(-10,10),a=a,b=b,tol=0.0001)
# 打印方程的根x
> result$root
[1] -2
一元一次方程非常容易解得,方程的根是-2!
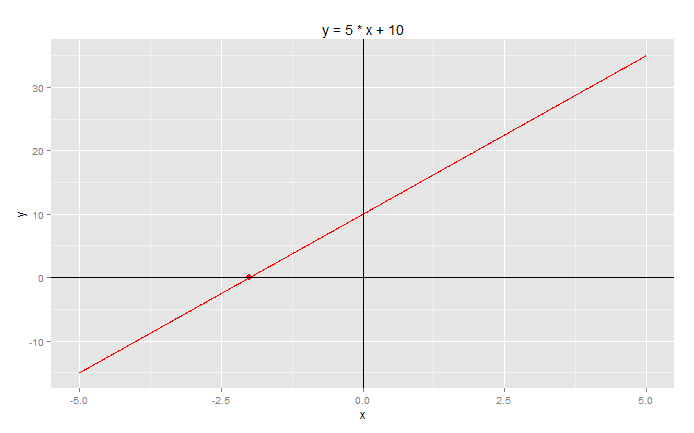
以图形展示方程:y = 5*x + 10
# 创建数据点
> x<-seq(-5,5,by=0.01)
> y<-f1(x,a,b)
> df<-data.frame(x,y)
# 用ggplot2来画图
> g<-ggplot(df,aes(x,y))
> g<-g+geom_line(col='red') #红色直线
> g<-g+geom_point(aes(result$root,0),col="red",size=3) #点
> g<-g+geom_hline(yintercept=0)+geom_vline(yintercept=0) #坐标轴
> g<-g+ggtitle(paste("y =",a,"* x +",b))
> g
4.2 一元二次方程
一元二次方程:a*x^2+b*x+c=0,设a=1,b=5,c=6,求x?
> f2 <- function (x, a, b, c) a*x^2+b*x+c
> a<-1;b<-5;c<-6
> result <- uniroot(f2,c(0,-2),a=a,b=b,c=c,tol=0.0001)
> result$root
[1] -2
把参数带入方程,用uniroot()函数,我们就解出了方程的一个根,改变计算的区间,我们就可以得到另一个根。
> result <- uniroot(f2,c(-4,-3),a=a,b=b,c=c,tol=0.0001)
> result$root
[1] -3
方程的两个根,一个是-2,一个是-3。
由于uniroot()函数,每次只能计算一个根,而且要求输入的区间端值,必须是正负号相反的。如果我们直接输入一个(-10,0)这个区间,那么uniroot()函数会出现错误。
> result <- uniroot(f2,c(-10,0),a=a,b=b,c=c,tol=0.0001)
Error in uniroot(f2, c(-10, 0), a = a, b = b, c = c, tol = 1e-04) :
位于极点边的f()值之正负号不相反
这应该是uniroot()为了统计计算对一元多次方程而设计的,所以为了使用uniroot()函数,我们需要取不同的区别来获得方程的根。
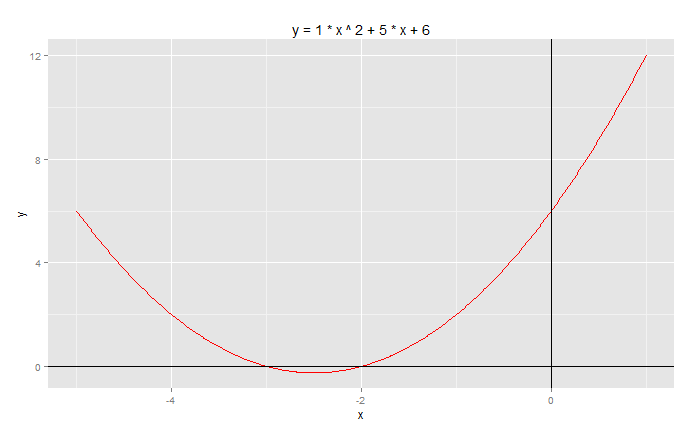
以图形展示方程:y = x^2 + 5*x + 6
# 创建数据点
> x<-seq(-5,1,by=0.01)
> y<-f2(x,a,b,c)
> df<-data.frame(x,y)
# 用ggplot2来画图
> g<-ggplot(df,aes(x,y))
> g<-g+geom_line(col='red') #红色曲线
> g<-g+geom_hline(yintercept=0)+geom_vline(yintercept=0) #坐标轴
> g<-g+ggtitle(paste("y =",a,"* x ^ 2 +",b,"* x +",c))
> g
我们从图,并直接的看到了x的两个根取值范围。
4.3 一元三次方程
一元二次方程:a*x^3+b*x^2+c*x+d=0,设a=1,b=5,c=6,d=-11,求x?
> f3 <- function (x, a, b, c,d) a*x^3+b*x^2+c*x+d
> a<-1;b<-5;c<-6;d<--11
> result <- uniroot(f3,c(-5,5),a=a,b=b,c=c,d=d,tol=0.0001)
> result$root
[1] 0.9461458
如果我们设置对了取值区间,那么一下就得到了方程的根。
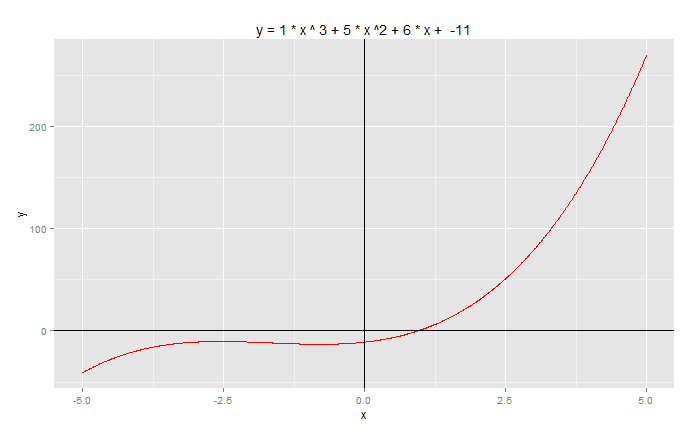
以图形展示方程:y = x^2 + 5*x + 6
# 创建数据点
> x<-seq(-5,5,by=0.01)
> y<-f3(x,a,b,c,d)
> df<-data.frame(x,y)
# 用ggplot2画图
> g<-ggplot(df,aes(x,y))
> g<-g+geom_line(col='red') # 3次曲线
> g<-g+geom_hline(yintercept=0)+geom_vline(yintercept=0) #坐标轴
> g<-g+ggtitle(paste("y =",a,"* x ^ 3 +",b,"* x ^2 +",c,"* x + ",d))
> g
4.4 二元一次方程组
R语言还可以解二次的方程组,当然计算方法,其实是利用于矩阵计算。
假设方程组:是以x1,x2两个变量组成的方程组,求x1,x2的值
以矩阵形式,构建方程组
# 左矩阵
> lf<-matrix(c(3,5,1,2),nrow=2,byrow=TRUE)
# 右矩阵
> rf<-matrix(c(4,1),nrow=2)
# 计算结果
> result<-solve(lf,rf)
> result
[,1]
[1,] 3
[2,] -1
得方程组的解,x1, x2分别为3和-1。
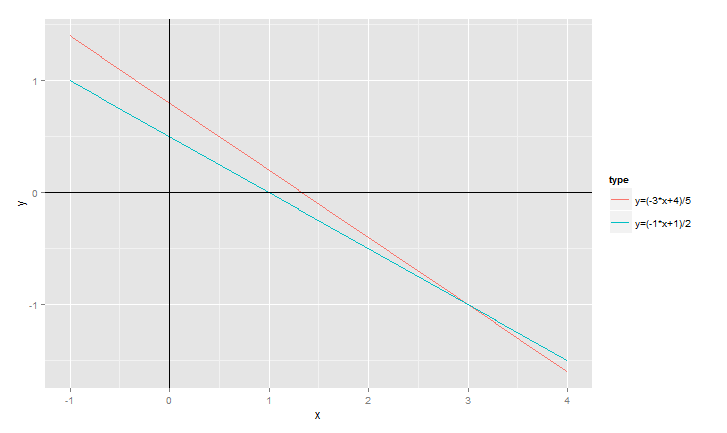
接下来,我们画出这两个线性方程的图。设y=X2, x=X1,把原方程组变成两个函数形式。
# 定义2个函数
> fy1<-function(x) (-3*x+4)/5
> fy2<-function(x) (-1*x+1)/2
# 定义数据
> x<-seq(-1,4,by=0.01)
> y1<-fy1(x)
> y2<-fy2(x)
> dy1<-data.frame(x,y=y1,type=paste("y=(-3*x+4)/5"))
> dy2<-data.frame(x,y=y2,type=paste("y=(-1*x+1)/2"))
> df <- rbind(dy1,dy2)
# 用ggplot2画图
> g<-ggplot(df,aes(x,y))
> g<-g+geom_line(aes(colour=type,stat='identity')) #2条直线
> g<-g+geom_hline(yintercept=0)+geom_vline(yintercept=0) #坐标轴
> g
我们看到两条直线交点的坐标,就是方程组的两个根。多元一次方程,同样可以用这种方法来解得。
通过R语言,我们实现了对于初等数学的各种计算,真的是非常方便!下一篇文章将介绍,用R语言来解决高级数学中的计算问题。
转载请注明出处:
http://blog.fens.me/r-mathematics/


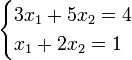
arcsec(x)!=1/arcsin(x),两个函数的定义域都不一样
我没明白你的问题,你是想说文章中哪里错了吗?
是的,注意文中反三角函数画图的公式,例如arcsec的公式是y=1/asin(x),应该是y=arccos(1/x),因为arcsec(x)=arccos(1/x)
请问老师 极点边的正负号相反是什么意思 我在求解一个方程的时候就需要自己预估计这个方程的区间么,,,
?没明白。
再次请教老师 R语言能直接求解一元二次方程么
可以啊,上文有例子。
老师 用R语言可以解AX=0 的基础解系?
基础解系,是线性代数吧?R对于线性代码支持的很好,应该可以解。
是线性代数 但是我在网上找了很久 目前还没有很好的包来处理这个问题,只能自己写程序来解决了。
你找个具体的问题列出来,我有时间帮你看一下。
請問如何求方程式 y=80+2a+3b-ab-1.5a^2-2b^2 之最佳解、函數值及特徵根?
试试用遗传算法找到最优解吧,http://blog.fens.me/algorithm-ga-r/