R的极客理想系列文章,涵盖了R的思想,使用,工具,创新等的一系列要点,以我个人的学习和体验去诠释R的强大。
R语言作为统计学一门语言,一直在小众领域闪耀着光芒。直到大数据的爆发,R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入,R语言的社区在迅速扩大成长。现在已不仅仅是统计领域,教育,银行,电商,互联网….都在使用R语言。
要成为有理想的极客,我们不能停留在语法上,要掌握牢固的数学,概率,统计知识,同时还要有创新精神,把R语言发挥到各个领域。让我们一起动起来吧,开始R的极客理想。
关于作者:
- 张丹(Conan), 程序员/Quant: Java,R,Nodejs
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-na-mice
前言
在进行数据分析时,从真实场景中所获得的数据经常是有缺失的,缺失数据会给我们数据分析造成很大的麻烦。很多的时候,我们需要先对缺失数据进行填充。数据缺失的原因是各种各样的,所以填充方法也有很多种,要找到符合业务特点的填充方法,不能因为填充而导致原数据集特征的巨变。
本文通过mice包提供的方法,合理地估算缺失值的分布,再进行填充,确保填充的数据是合理的。
目录
- 缺失的数据
- 准备数据集
- mice包介绍
- 填充方法和程序实现
1. 缺失的数据
缺失值的处理,是数据预处理过程中的重要环节,造成数据缺失的原因有很多,我发现的最主要的原因是,业务允许为空值导致数据集有缺失值,还包括比如,数据丢失、存储故障和拒绝填写信息等原因。
如果数据量很大而缺失值量很少,那么我们直接去除这些数据就行了,也不会有太多的影响。缺失值处理主要讨论的是,数据量不太大,而缺失值的数据的影响又比较关键时,这个时候就需要用到一些方法对缺失值数据进行填充。
1.1 缺失机制分类
Little和Ruth(1987)把数据缺失的机制分为三类:
- 完全随机缺失(missing completely at random, MCAR)
所缺失的数据是完全随机的,缺失发生的概率既与已观察到的数据无关,也与未观察到的数据无关。这是一种比较理想的情况。 - 随机缺失(missing at random, MAR)
数据的缺失不是完全随机的。缺失数据发生的概率与所观察到的变量是有关的,而与未观察到的数据的特征是无关的。这是一个比较严重的问题,在这种情况下,我们需要进一步检查数据收集过程,并尝试了解数据为什么丢失。 例如,如果在一项问卷调查中,大多数人没有回答某个问题,他们为什么这么做,是问题不清楚吗? - 不可忽略的缺失(non-ignorable missing ,NIM),亦称为非随机缺失(not missing at random, NMAR),也有研究者将其称为MNAR(missing not at random)。
缺失数据不仅依赖于其它变量,又依赖于变量本身,这种缺失即为不可忽略的缺失。
假设数据缺失是完全随机缺失(MCAR),如果数据缺失太多,也可能造成很大的问题。 一般来说,数据的缺失量小于数据总量的5%是可以接受的。如果某个特征或样本的缺失数据量超过20%,那么您可考虑是否需要留下该特征或样本。
1.2 填充方法
对于缺失值的填充方法分为单变量填充和多变量填充。单变量填补,包括简单随机填充,均值/中位数/分位数填充,回归填充,热平台和冷平台。多变量填补,使用回归插补法。
下面分别介绍一下,这种填充的方法:
简单随机填补:对于每一个缺失值,从已有的该变量数据中随机抽样作为填补值,填补进缺失位置。仅仅考虑到了缺失变量本身,而并没有考虑到相关变量的信息。因此,信息量的利用少。
均值/中位数/分位数填补:用存在缺失值的变量的已有值的均值/中位数/分位数,作为填补值。这种方法显然会导致方差偏小。
回归填补:将缺失变量作为因变量,相关变量(其他变量)作为自变量,进行回归拟合,用预测值作为填补值。用于作为自变量的变量最好是具有完全数据(无缺失)。
热平台和冷平台:热平台法又称匹配插补法,思路是在完全数据样本中,找到一个和具有缺失值的样本相似的完全数据样本,用完全数据样本值作为填充值,其过程有点类似于K阶近邻的思想。冷平台法又称条件均值插补法,思路是先将总体分层(聚类),采用样本所在层(类)的完全数据的均值来替代缺失值。
回归插补法:对缺失变量和完全数据变量拟合多元回归模型来预测缺失值,是多重填补法的一种应用(Multiple Imputation Missing Data)。本文主要就介绍这种方法,利用mice包进行实现。
2. 准备数据集
为了进行空值的数据处理,我们使用一个R语言中自带的数据集airquality。airquality数据集,记录了1973年5月至9月在纽约进行的每日空气质量测量。
开发所使用的系统环境
- Win10 64bit
- R: 3.6.1 x86_64-w64-mingw32/x64 b4bit
数据集包括153条记录,6列:
- Ozone: 臭氧浓度(ppb)
- Solar.R: 太阳辐射量(lang)
- Wind: 风速(MPH)
- Temp: 温度(°F)
- Month: 发生月
- Day:发生日
# 查看数据集
> head(airquality)
Ozone Solar.R Wind Temp Month Day
1 41 190 7.4 67 5 1
2 36 118 8.0 72 5 2
3 12 149 12.6 74 5 3
4 18 313 11.5 62 5 4
5 NA NA 14.3 56 5 5
6 28 NA 14.9 66 5 6
查看数据统计概率, Ozone列有37条空值,Solar.R列有7条空值,Wind列有7条空值。
> summary(airquality)
Ozone Solar.R Wind Temp Month Day
Min. : 1.00 Min. : 7.0 Min. : 1.700 Min. :56.00 Min. :5.000 Min. : 1.0
1st Qu.: 18.00 1st Qu.:115.8 1st Qu.: 7.400 1st Qu.:72.00 1st Qu.:6.000 1st Qu.: 8.0
Median : 31.50 Median :205.0 Median : 9.700 Median :79.00 Median :7.000 Median :16.0
Mean : 42.13 Mean :185.9 Mean : 9.958 Mean :77.88 Mean :6.993 Mean :15.8
3rd Qu.: 63.25 3rd Qu.:258.8 3rd Qu.:11.500 3rd Qu.:85.00 3rd Qu.:8.000 3rd Qu.:23.0
Max. :168.00 Max. :334.0 Max. :20.700 Max. :97.00 Max. :9.000 Max. :31.0
NA's :37 NA's :7
计算缺失值比例
# 定义缺失值比例计算函数miss()
> miss <- function(x){sum(is.na(x))/length(x)}
列,缺失值比例
> apply(airquality,2,miss)
Ozone Solar.R Wind Temp Month Day
0.24183007 0.04575163 0.00000000 0.00000000 0.00000000 0.00000000
Ozone列的缺少值比例最高,达到24%,我们可以考虑移除这个变量。
行,缺失值比例。
# 计算行的缺失值比例,取前30条记录
> head(apply(airquality,1,miss),30)
[1] 0.0000000 0.0000000 0.0000000 0.0000000 0.3333333 0.1666667 0.0000000 0.0000000 0.0000000 0.1666667
[11] 0.1666667 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000
[21] 0.0000000 0.0000000 0.0000000 0.0000000 0.1666667 0.1666667 0.3333333 0.0000000 0.0000000 0.0000000
其中,第5个值缺失值表示第5行缺失比例为33%,表示前6列中有2列是空的。
3. mice包介绍
mice包实现了,多变量缺失数据填补的方法,基于多元回归模型来预测,每个不完整变量由单独的模型估算,进行多重混合评估。mice包算法可以实现对于连续型,二进制,无序分类和有序分类数据的进行混合。此外,mice包可以处理连续的两级数据,并通过被动插补来保持插补之间的一致性,通过第各种统计诊断图,保证插补数据的质量。
按照mice包把缺失值的处理形成了一套流程,通过链式方程形成多重填补法。
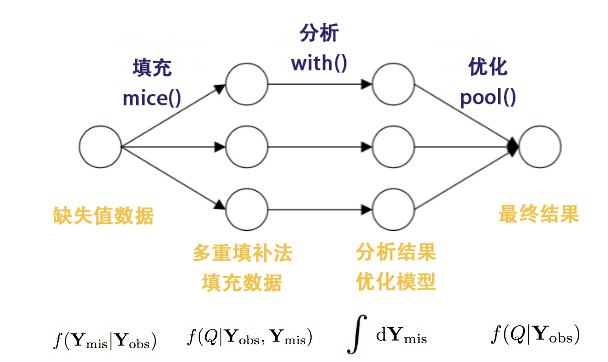
对于缺失值数据的处理,用3个步骤来进行定义。
- 填充:mice()函数,从一个包含缺失数据的数据框开始,然后返回一个包含多个完整数据集的对象,每个完整数据集都是通过对原始数据框中的缺失数据进行插而生成的。
- 分析:with()函数,可依次对每个完整数据集应用统计模型,分析填充的结果。
- 优化:pool()函数,将这些单独的分析结果整合为一组结果,最终模型的标准误和p值,都将准确地反映出由于缺失值和多重插补而产生的不确定性。
4. 填充方法和程序实现
接下来,我们使用mice包,对airquality数据集的缺失值进行填充。操作步骤按,观察缺失值,多重填补法,分析结果优化模型,获得最终结果。
4.1 观察缺失值
对于上面的数据集,我们可以用mice包来观察数据。用md.pattern()函数来判断行的缺失值。
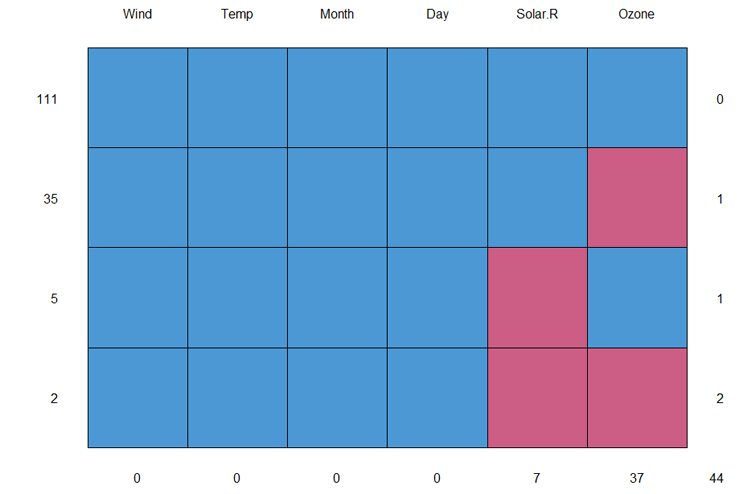
> md.pattern(airquality)
Wind Temp Month Day Solar.R Ozone
111 1 1 1 1 1 1 0
35 1 1 1 1 1 0 1
5 1 1 1 1 0 1 1
2 1 1 1 1 0 0 2
0 0 0 0 7 37 44
数据解读:
- 左边第一列,为样本数
- 右边第一列,为累积缺失值个数,0为没有缺失。
- 最下面一行,每个列有多少个缺失值
举例解释一下:第一行可以理解为,有111条记录,所有列都有值,没有缺失值。第二行可以理解为,有35条记录,Ozone列有缺失值。
接下来,以行和列进行配对处理,按4种模式分别展示出缺失值。
- rr:行有值,列有值
- rm:行有值,列丢失
- mr:行丢失,列有值
- mm:行丢失,列丢失
> md.pairs(airquality)
$rr
Ozone Solar.R Wind Temp Month Day
Ozone 116 111 116 116 116 116
Solar.R 111 146 146 146 146 146
Wind 116 146 153 153 153 153
Temp 116 146 153 153 153 153
Month 116 146 153 153 153 153
Day 116 146 153 153 153 153
$rm
Ozone Solar.R Wind Temp Month Day
Ozone 0 5 0 0 0 0
Solar.R 35 0 0 0 0 0
Wind 37 7 0 0 0 0
Temp 37 7 0 0 0 0
Month 37 7 0 0 0 0
Day 37 7 0 0 0 0
$mr
Ozone Solar.R Wind Temp Month Day
Ozone 0 35 37 37 37 37
Solar.R 5 0 7 7 7 7
Wind 0 0 0 0 0 0
Temp 0 0 0 0 0 0
Month 0 0 0 0 0 0
Day 0 0 0 0 0 0
$mm
Ozone Solar.R Wind Temp Month Day
Ozone 37 2 0 0 0 0
Solar.R 2 7 0 0 0 0
Wind 0 0 0 0 0 0
Temp 0 0 0 0 0 0
Month 0 0 0 0 0 0
Day 0 0 0 0 0 0
为了让可视化效果更强一点,我可以引入VIM包,进行可视化。
# 加载VIM包
> library(VIM)
> mice_plot <- aggr(airquality, col=c('navyblue','yellow'),
+ numbers=TRUE, sortVars=TRUE,
+ labels=names(airquality), cex.axis=.7,
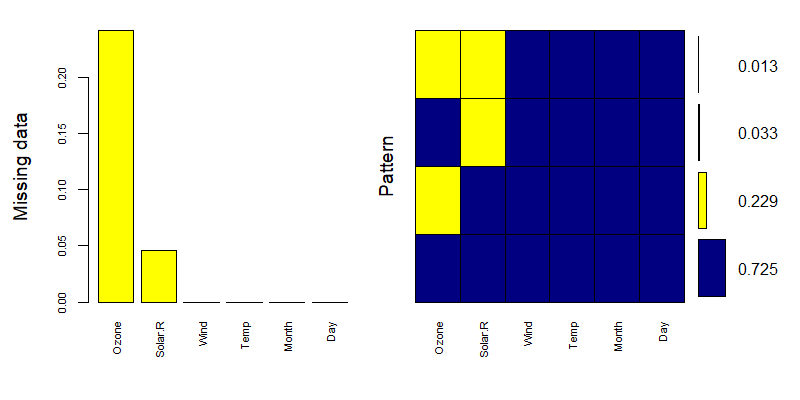
+ gap=3, ylab=c("Missing data","Pattern"))
Variables sorted by number of missings:
Variable Count
Ozone 0.24183007
Solar.R 0.04575163
Wind 0.00000000
Temp 0.00000000
Month 0.00000000
Day 0.00000000
左侧图显示了每个字段中缺失样本数量占比。右侧图每一行代表了一种缺失模式,黄色代表缺失,蓝色代表未缺失,右侧图例表示此模式数量,可与md.pattern()结果对应观察。
画出数据集 airquality 的各列的数据分布。
> matrixplot(airquality)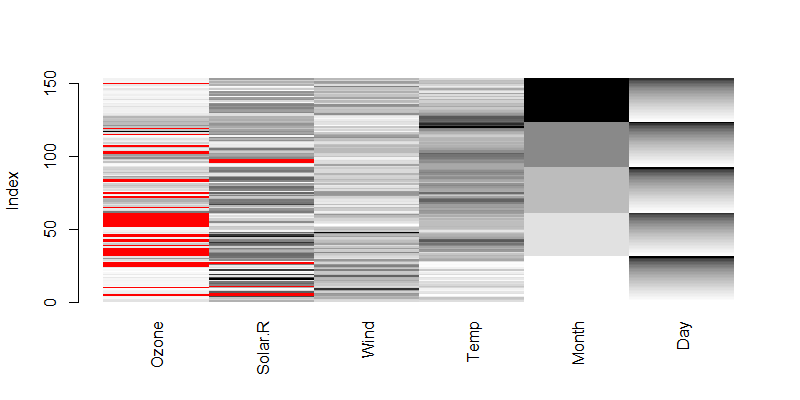
图中,红色表示缺失值,从黑色到灰色再到白色的过渡色表示值的不同,过渡色越多表示数据取值越分散,过渡色越少表示数据取值越集中。Month列,只有5个颜色,表示只有5个取值。
我们还可以用散点图,来观察两个变量之间的缺失值的关系。画出Ozone和Solar.R列的空缺值的分布散点图。
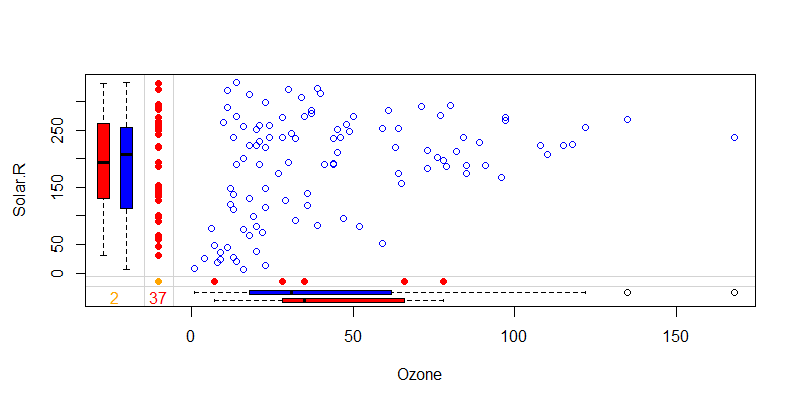
> marginplot(airquality[c(1,2)], col = c("blue", "red", "orange"))
x轴为Ozone列,y轴为Solar.R列,蓝色点为数据散点图,红色点分别表示Ozone的缺失值和Solar.R列的缺失值位置。
4.2 多重填补法
接下来,使用mice()函数进行数据填充,
# 进行填充
> imputed_Data <- mice(airquality, m=5, maxit = 50, method = 'pmm', seed = 500)
iter imp variable
1 1 Ozone Solar.R
1 2 Ozone Solar.R
1 3 Ozone Solar.R
1 4 Ozone Solar.R
1 5 Ozone Solar.R
2 1 Ozone Solar.R
2 2 Ozone Solar.R
2 3 Ozone Solar.R
2 4 Ozone Solar.R
2 5 Ozone Solar.R
// 省略输出
参数解读:
- airquality, 原始数据集
- m, 多重填补法的填补矩阵数,默认为5次
- maxit,最大迭代次数,默认5次
- method, 填补用的方法,pmm为预测均值匹配(predictive mean matching)。用methods(mice) 可以看到有哪些可用的方法。
查看统计结果,输出填充算法,预测矩阵predictorMatrix。填充算法这里使用的是pmm, 除了pmm还有很多种。预测矩阵中,显示为1的位置是会进行填充值的位置,如果不想进行填充,可以修改矩阵中的值为0.
> summary(imputed_Data)
Class: mids
Number of multiple imputations: 5
Imputation methods:
Ozone Solar.R Wind Temp Month Day
"pmm" "pmm" "" "" "" ""
PredictorMatrix:
Ozone Solar.R Wind Temp Month Day
Ozone 0 1 1 1 1 1
Solar.R 1 0 1 1 1 1
Wind 1 1 0 1 1 1
Temp 1 1 1 0 1 1
Month 1 1 1 1 0 1
Day 1 1 1 1 1 0
查看填补的结果
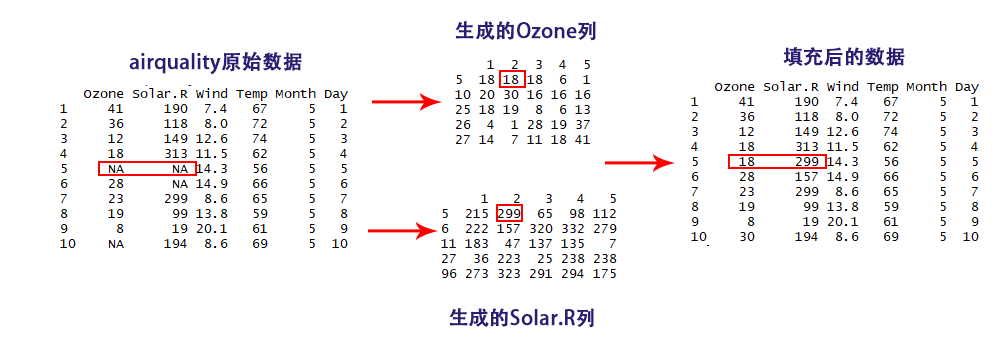
> imputed_Data$imp
$Ozone
1 2 3 4 5
5 18 18 18 6 1
10 20 30 16 16 16
25 18 19 8 6 13
26 4 1 28 19 37
27 14 7 11 18 41
32 59 40 44 23 31
33 36 7 13 65 41
// 省略输出
$Solar.R
1 2 3 4 5
5 215 299 65 98 112
6 222 157 320 332 279
11 183 47 137 135 7
27 36 223 25 238 238
96 273 323 291 294 175
97 287 275 285 31 237
98 323 187 294 320 264
// 省略输出
以$Ozone为例,左边第一列为缺失值的行号,其他每一列都为每次pmm算法生成的填充结果,每一行表示生成的5次结果分别是什么值。
分面板观察,以独立的各个指标进行分组,5组数据的填充情况。
> stripplot(imputed_Data, col=c("grey",mdc(2)),pch=c(1,20))每一个面板为一个列的原始数据和5次填充的数据,灰色散点为原始数据取值的分布,红色的小点为填充的数据取值的分布。
分面板观察,以Ozone和Solar.R做进行分组组合,观察5组数据的填充情况。
> xyplot(imputed_Data , Ozone ~ Solar.R | .imp, pch=20,cex=1.2)
每一个面板为一个列的原始数据和5次填充的数据,x轴为Solar.R,y轴为Ozone,蓝色散点为原始数据取值的分布,红色的小点为填充的数据取值的分布。
3.3 分析结果,优化模型
使用生成的填补的结果,应用统计模型,对每个完整的数据集进行评价。这里我们以多元线性回归模型作为评价填充值好坏的模型。
使用with()函数,对5组插补数据集进行多元线性回归分析模型,进行T检验,判断数据集中每个变量的有效性。
> fit=with(imputed_Data,lm(Ozone ~ Wind + Solar.R + Temp))
# 查看统计结果
> summary(fit)
# A tibble: 20 x 5
term estimate std.error statistic p.value
<chr> <dbl> <dbl> <dbl> <dbl>
1 (Intercept) -39.9 19.1 -2.09 3.87e- 2
2 Wind -3.60 0.549 -6.55 8.90e-10
3 Solar.R 0.0572 0.0200 2.87 4.72e- 3
4 Temp 1.38 0.213 6.46 1.39e- 9
5 (Intercept) -69.2 19.7 -3.51 5.99e- 4
6 Wind -3.24 0.567 -5.71 5.81e- 8
7 Solar.R 0.0582 0.0204 2.86 4.84e- 3
8 Temp 1.71 0.218 7.85 7.50e-13
9 (Intercept) -59.5 19.2 -3.10 2.34e- 3
10 Wind -3.13 0.550 -5.68 6.85e- 8
11 Solar.R 0.0571 0.0198 2.88 4.54e- 3
12 Temp 1.57 0.215 7.29 1.66e-11
13 (Intercept) -67.4 18.5 -3.64 3.73e- 4
14 Wind -2.94 0.531 -5.53 1.41e- 7
15 Solar.R 0.0668 0.0189 3.54 5.40e- 4
16 Temp 1.61 0.204 7.87 6.83e-13
17 (Intercept) -38.4 21.6 -1.78 7.69e- 2
18 Wind -3.99 0.620 -6.44 1.52e- 9
19 Solar.R 0.0523 0.0223 2.34 2.05e- 2
20 Temp 1.44 0.239 6.04 1.15e- 8
多元线性模型y=a*x1+b*x2+c*x3+e,x1=Wind,x2=Solar.R,x3=Temp, e=Intercept,上面数据集以每4行为一组,每组分别为多元线性回归的结果。关于多元线性回归的详细介绍,请参考文章R语言解读多元线性回归模型
数据解释
- term,变量
- estimate ,参数估计值
- std.error,残差的标准误差
- statistic,t统计量
- p.value,p-value值
4.4 模型评估
使用pool()函数,将5个单独回归模型进行汇总,整理模型的标准误和p值等多个评价参数,进行F检验,判断模型整体拟合的有效性。pooled对象是一个包含这m个统计分析平均结果的列表对象,准确地反映出由于缺失值和多重插补而产生的不确定性。
> pooled=pool(fit)
> pooled
Class: mipo m = 5
estimate ubar b t dfcom df riv
(Intercept) -54.87825512 3.864370e+02 2.189907e+02 6.492258e+02 149 19.08909 0.68003032
Wind -3.37959755 3.186764e-01 1.758552e-01 5.297026e-01 149 19.61464 0.66219610
Solar.R 0.05833371 4.121520e-04 2.745861e-05 4.451024e-04 149 114.74908 0.07994702
Temp 1.54135605 4.758977e-02 1.736383e-02 6.842637e-02 149 30.33948 0.43783767
lambda fmi
(Intercept) 0.40477265 0.45866597
Wind 0.39838627 0.45159195
Solar.R 0.07402865 0.08975652
Temp 0.30451120 0.34623283
指标解读:
- mipo,一种数据结构,pool用于产生mipo对象
- m, m=5 多组插补数据
- estimate,估计值,pool汇总的完整数据估计
- ubar, 估计的内插方差,std.error的平方的均值,越小越好
- b,估计之间的插补方差, estimate的方差,越小越好
- t,估计的总方差,ubar + (1 + 1 / m) * b, 越小越好
- dfcom,完整数据的自由度
- df,t统计量的自由度,由Barnard-Rubin提供一种自由度的计算方法,越小越好
- riv,方差的相对增加,(1 + 1 / m) * b / ubar,越小越好
- lambda, 缺失值的比例,(1 + 1 / m) * b / t,越小越好
- fmi, 缺少信息的部分,(riv + 2 / (df + 3)) / (riv + 1)),越小越好
对插补的结果,再进行R^2检验。
> pool.r.squared(fit)
est lo 95 hi 95 fmi
R^2 0.5630547 0.4404848 0.6677567 NaN
指标解读:
- est, 合并的R^2,估计值
- lo 95,合并的R^2,95%下限
- hi 95,合并的R^2,95%上限
- fmi,缺少信息的部分,越小越好
pool的过程,主要就是完成F检验和R^2检验。
3.4 最终结果
最后,根据检验统计量,我们选择以第2次pmm的结果做为填充,获得填充后的数据集。
> completeData <- complete(imputed_Data,2)
> completeData
Ozone Solar.R Wind Temp Month Day
1 41 190 7.4 67 5 1
2 36 118 8.0 72 5 2
3 12 149 12.6 74 5 3
4 18 313 11.5 62 5 4
5 18 299 14.3 56 5 5
6 28 157 14.9 66 5 6
7 23 299 8.6 65 5 7
8 19 99 13.8 59 5 8
9 8 19 20.1 61 5 9
10 30 194 8.6 69 5 10
mice包提供了29种填充算法,上面的例子我只是用到了pmm一种方法。大家可以根据不同的业务场景要求和数据的分布情况,用不同方法进行填充,让数据差异变化最小。
> methods(mice)
[1] mice.impute.2l.bin mice.impute.2l.lmer mice.impute.2l.norm mice.impute.2l.pan
[5] mice.impute.2lonly.mean mice.impute.2lonly.norm mice.impute.2lonly.pmm mice.impute.cart
[9] mice.impute.jomoImpute mice.impute.lda mice.impute.logreg mice.impute.logreg.boot
[13] mice.impute.mean mice.impute.midastouch mice.impute.norm mice.impute.norm.boot
[17] mice.impute.norm.nob mice.impute.norm.predict mice.impute.panImpute mice.impute.passive
[21] mice.impute.pmm mice.impute.polr mice.impute.polyreg mice.impute.quadratic
[25] mice.impute.rf mice.impute.ri mice.impute.sample mice.mids
[29] mice.theme
缺失数据处理,通常都是一种复杂的不确定问题,非常棘手。通过使用mice包,我们可以高效地完成复杂的缺失数据填充,把数据缺失问题转化成统计问题,用统计量来评估插值对于原数据集的影响。非常强大的工具,让我们少拍脑袋,科学处理数据问题。
转载请注明出处:
http://blog.fens.me/r-na-mice




请问怎么决定最后选择第二次模拟的数据?我简单看过Buuren2011年的文章,但没有明白最后如何抉择哪一次模拟的数据。