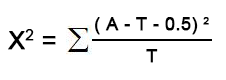R的极客理想系列文章,涵盖了R的思想,使用,工具,创新等的一系列要点,以我个人的学习和体验去诠释R的强大。
R语言作为统计学一门语言,一直在小众领域闪耀着光芒。直到大数据的爆发,R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入,R语言的社区在迅速扩大成长。现在已不仅仅是统计领域,教育,银行,电商,互联网….都在使用R语言。
要成为有理想的极客,我们不能停留在语法上,要掌握牢固的数学,概率,统计知识,同时还要有创新精神,把R语言发挥到各个领域。让我们一起动起来吧,开始R的极客理想。
关于作者:
- 张丹(Conan), 程序员/Quant: Java,R,Nodejs
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-test-x2
前言
做统计分析R语言是最好的,R语言对于统计检验有非常好的支持。我会分7篇文章,分别介绍用R语言进行统计量和统计检验的计算过程,包括T检验,F检验,卡方检验,P值,KS检验,AIC,BIC等常用的统计检验方法和统计量。
本文是第三篇卡方检验,卡方检验关注点用于测量实际值与预测值的差距,对于预测类的模型能给出了客观地评价方法。
目录
- 卡方检验介绍
- 数据集
- 四格表法推导过程
- 程序实现
1. 卡方检验介绍
卡方检验,又称χ2检验,是一种非参数检验,主要是比较两个以及两个以上样本率以及两个分类变量之间是否具有显著的相关性,其根本思想是统计样本的实际观测值与理论推断值之间的偏离程度。卡方检验,是由英国统计学家Karl Pearson在1900年首次提出的,在《哲学杂志》上发表。
卡方检验,实际观测值与理论推断值之间的偏离程度就决定卡方值的大小,如果卡方值越大,两个变量偏差程度越大;反之,卡方值越小两个变量偏差越小;如果两个变量的完全相等,卡方值就为0,表明观测值与理论值完全符合。
通常卡方检验的主要应用方向为:卡方拟合优度检验,卡方独立性检验。卡方检验可以分为成组比较(不配对资料)和个别比较(配对,或同一对象两种处理的比较)两类。卡方检验试用条件包括,随机样本数据,卡方检验的理论频数不能太小。
卡方检验的计算公式:
- χ2,为统计量,用于衡量实际值与理论值的差异程度。
- A,为实际值
- T,为理论值
- 自由度,df = n-1
卡方检验有3种推导过程:四格表法的卡方检验,行列表法的卡方检验,列联表法的卡方检验,本文将介绍四格表法的卡方检验。
2. 数据集
卡方检验,对于数据有比较严格的要求,所以我们需要先找到一个合适的数据集,作为测试数据集。
我们以“抛硬币”来作为卡方检验的使用场景。对于1次抛硬币来说,只有2种结果,正面是字,反面是头像,两种结果的出现概率相同都是50%,且每次抛硬币都是独立事件。那么,根据这个抛硬币的结果做出假设,原假设(H0)抛硬币出现正面和反面的概率都是50%,为验证这个假设成立,就是卡方检验。
开发环境所使用的系统环境
- Win10 64bit
- R: 3.6.1 x86_64-w64-mingw32/x64 b4bit
接下来,用随机过程模拟抛硬币的过程,设置抛硬币100次,1为正面,0为反面。
> N=100 # 抛硬币100次
> set.seed(1) # 随机种子
> coin<-sample(x=c(0,1), prob=c(0.5,0.5),size = N, replace = TRUE) # 模拟抛硬币
> coin # 打印结果
[1] 1 1 0 0 1 0 0 0 0 1 1 1 0 1 0 1 0 0 1 0 0 1 0 1 1 1 1 1 0 1 1 0 1 1 0 0 0 1 0 1 0 0 0 0
[45] 0 0 1 1 0 0 1 0 1 1 1 1 1 0 0 1 0 1 1 1 0 1 1 0 1 0 1 0 1 1 1 0 0 1 0 0 1 0 1 1 0 1 0 1
[89] 1 1 1 1 0 0 0 0 1 1 0 0
统计抛硬币的结果
> table(coin) # 统计0和1的出现次数
coin
0 1
48 52
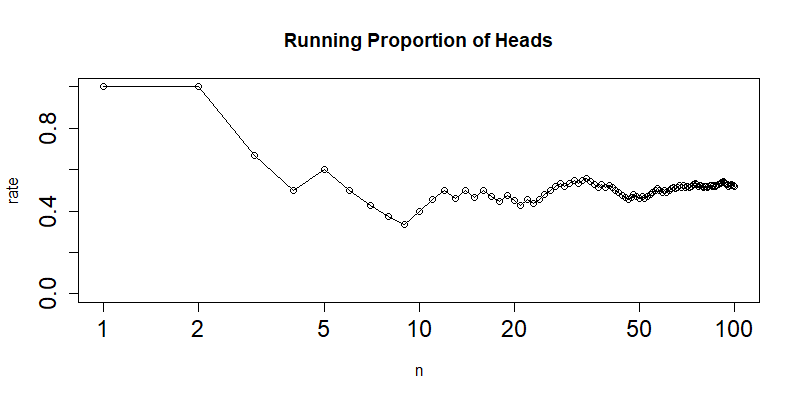
用可视化展示累积的正面出现概率
> cnt <- cumsum(coin) # 积累求和,正面1出现的次数
> n<-1:N # 次数向量
> rate<- cnt/1:N # 累积的正面出现概率
> plot(n,rate,type="o",log="x", # 画图,x轴做log变型
+ xlim=c(1,N), ylim=c(0.0,1.0), cex.axis=1.5,
+ main="Running Proportion of Heads",cex.axis=1.5)
接下来,我们就以coin作为数据集,进行卡方检验的数据集。
3. 四格表法推导过程
四格表法的卡方检验,用于进行两个样本率或两个样本构成比的比较。
我们可以把抛硬币的过程,分成观察组和期望组,观察组就是上面随机过程的结果,期望组是我们根据概率的公式给出来的,把数据填入下面表格。
| 正面 | 反面 | 合计 | |
| 观察次数 | 52 | 48 | 100 |
| 期望次数 | 50 | 50 | 100 |
| 合计 | 102 | 98 | 200 |
通过简单的计算,我们得出观察组的正面概率为52%和期望组的正面概率为50%,两者的差别可能是误差导致,也有可能是受到抛硬币的次数影响的。
为了确定真实原因,我们先假设抛硬币是符合大数定理的,是不受抛硬币的次数影响的,即抛硬币的次数和概率无关,我们可以得出正面结果的实际是(52+50) / (52+48+50+50)= 0.51 = 51%。
可推到出:
| 正面 | 反面 | 合计 | |
| 观察次数 | 100*0.51 =51 | 100*(1-0.51) = 49 | 100 |
| 期望次数 | 100*0.51 =51 | 100*(1-0.51) = 49 | 100 |
| 合计 | 102 | 98 | 200 |
如果抛硬币次数与正面结果的概率是独立无关的,那么四格表里的理论值和实际值差别应该会很小。
代入公式进行计算。
X^2 = (52- 51)^2 / 51 + (48 - 49)^2 / 49 + (50 - 51)^2 / 51 + (50 - 49)^2 / 49 = 0.08003201
当以四格表法进行卡方检验时,还有一些限制条件,当两个独立样本比较时,需要分成以下3种情况:
- 所有的理论数T≥5并且总样本量n≥40,用Pearson卡方进行检验.
- 如果理论数T<5但T≥1,并且n≥40,用连续性校正的卡方进行检验.
- 如果有理论数T<1或n<40,则用Fisher’s检验.
根据限制条件,由于样本数据量为200大于40,所以需要对原公式进行修正。
修正公式为:
X^2 = (abs(52- 51)-0.5)^2 / 51 + (abs(48 - 49)-0.5)^2 / 49 + (abs(50 - 51)-0.5)^2 / 51 + (abs(50 - 49)-0.5)^2 / 49
= 0.020008
最后,算出卡方统计量为0.020008。下面我们再用R语言的程序来算一下,看看是否是相同的结果。
4. 程序实现
用程序实现卡方检验,可以直接使用chisq.test()函数。
# 合并观测值和期望值,形成矩阵
> s<-c(table(coin),c(50,50))
> x <- matrix(s, ncol = 2, byrow=TRUE)
> x
[,1] [,2]
[1,] 48 52
[2,] 50 50
# 卡方检验
> chisq.test(x)
Pearson's Chi-squared test with Yates' continuity correction
data: x
X-squared = 0.020008, df = 1, p-value = 0.8875
指标解释:
- H0:抛硬币出现正面和反面的概率都是50%,与次数无关
- X-squared统计量:0.020008
- df,自由度,1
- p-value值:0.8875
结果解读,以0.05为显著性水平,自由度df=1,统计量X-squared = 0.020008 小于临界值0.455(查表),说明X-squared值不显著,不能拒绝原假设。以0.05为显著性水平,p-value=0.8875大于0.05,所以不能拒绝原假设,说明抛硬币的次数与结果为正面的概率是没有关系的。这个结果与我们构造的数据是一致的,也是符合大数定理的。
查看观察值和期望值。
# 查看观察值
> chi$observed
[,1] [,2]
[1,] 48 52
[2,] 50 50
# 查看期望值
> chi$expected
[,1] [,2]
[1,] 49 51
[2,] 49 51
# 残差
> chi$residuals
[,1] [,2]
[1,] -0.1428571 0.140028
[2,] 0.1428571 -0.140028
手动计算X^2值和P值,关于P值的详细解释,请查看文章R语言实现统计检验-P值
# 手动计算X^2值
> sr <- rowSums(x)
> sc <- colSums(x)
> n <- sum(x)
> E <- outer(sr, sc, "*")/n;E
[,1] [,2]
[1,] 49 51
[2,] 49 51
> x2 <- sum((abs(x - E) - 0.5)^2/E);x2
[1] 0.020008
# 手动计算P值
> pchisq(x2, 1, lower.tail = FALSE)
[1] 0.8875147
本文用R语言详细介绍了卡方检验的计算过程,x^2越小,越能验证假设是正确的,越能说明观测值与期望值是一致的,x^2越大,越证明假设是错误的,预测越不准。为预测类的模型提供了评价标准。
转载请注明出处:
http://blog.fens.me/r-test-x2