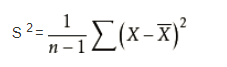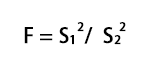• Posts tagged "F-Test"

Blog Archives

Posted:
Jul 29, 2019
Tags:
Comments:
2 Comments

用R语言解读统计检验-F检验

R的极客理想系列文章，涵盖了R的思想，使用，工具，创新等的一系列要点，以我个人的学习和体验去诠释R的强大。

R语言作为统计学一门语言，一直在小众领域闪耀着光芒。直到大数据的爆发，R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入，R语言的社区在迅速扩大成长。现在已不仅仅是统计领域，教育，银行，电商，互联网….都在使用R语言。

要成为有理想的极客，我们不能停留在语法上，要掌握牢固的数学，概率，统计知识，同时还要有创新精神，把R语言发挥到各个领域。让我们一起动起来吧，开始R的极客理想。

关于作者：

  • 张丹(Conan), 程序员/Quant: Java,R,Nodejs
  • blog: http://blog.fens.me
  • email: bsspirit@gmail.com

转载请注明出处：
http://blog.fens.me/r-test-f

前言

做统计分析R语言是最好的，R语言对于统计检验有非常好的支持。我会分7篇文章，分别介绍用R语言进行统计量和统计检验的计算过程，包括T检验，F检验，卡方检验，P值，KS检验，AIC，BIC等常用的统计检验方法和统计量。

本文是第二篇F检验，T检验关注点在均值，而F检验关注点在方差。

目录

  1. F检验介绍
  2. 数据集
  3. F检验实现

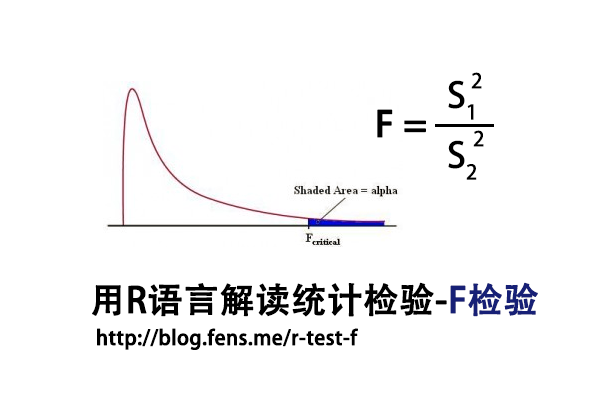
1. F检验介绍

F检验法(F-test)，初期叫方差比率检验(Variance Ratio)，又叫联合假设检验(Joint Hypotheses Test)，是英国统计学家Fisher提出的，主要通过比较两组数据的方差，以确定他们的密度是否有显著性差异。至于两组数据之间是否存在系统误差，则在进行F检验并确定它们的密度没有显著性差异之后，再进行T检验。

F检验，是一种在零假设(H0)之下，统计值服从F-分布的检验。

样本标准偏差的平方公式：

F统计量计算公式：


公式解释

  • F:统计量，根据自由度查表，当F值小于查表值时没有显著差异，当F值大于等于查表值时有显著差异
  • S1:样本1的标准差
  • S2:样本2的标准差
  • 分子自由度: df=分子的数量-1
  • 分母自由度: df=分母的数量-1

T检验和F检验对比
T检验用来检测数据的准确度(系统误差)，F检验用来检测数据的精密度(偶然误差)。在定量分析过程中，常遇到两种情况：一种是样本测量的平均值与真值不一致；另一种是两组测量的平均值不一致。

上述不一致是由于定量分析中的系统误差和偶然误差引起的，因此必须对两组分析结果的准确度或精密度是否存在显著性差异做出判断，两组数据的显著性检验顺序是先F检验后T检验。

T检验是检查两组均值的差异，而F检验是检查多组均值之间的差异。

对于多元线性回归模型，t检验是对于单个变量进行显著性，检验该变量独自对被解释变量的影响。f检验是检验回归模型的显著意义，即所有解释变量联合起来对被解释变量的影响，关于线性回归请参考文章，R语言解读一元线性回归模型和R语言解读多元线性回归模型。

2. 数据集

F检验，对于数据有比较严格的要求，所以我们需要先找到一个合适的数据集，作为测试数据集。我发现了R语言自带的一个数据集ToothGrowth，是很好的测试数据集，本文接下来的内容，将以这个数据集进行测试，来介绍F检验。

开发环境所使用的系统环境

  • Win10 64bit
  • R: 3.4.2 x86_64-w64-mingw32/x64 b4bit

数据集ToothGrowth，记录了60只豚鼠的牙齿生长速度，使用2种不同的方法(OJ和VC)，每天按3种不同的注射剂量进行注射，对牙齿的生长速度的对比数据，共3列，60条记录。

  • len列，为牙齿长度
  • supp列，为注射方法
  • dose列，为注射剂量

查看数据集，打印前10行


> head(ToothGrowth,10)
    len supp dose
1   4.2   VC  0.5
2  11.5   VC  0.5
3   7.3   VC  0.5
4   5.8   VC  0.5
5   6.4   VC  0.5
6  10.0   VC  0.5
7  11.2   VC  0.5
8  11.2   VC  0.5
9   5.2   VC  0.5
10  7.0   VC  0.5

F检验对于数据的正态性非常敏感，我们需要先对选定数据集进行进行正态分布检验。使用Shapiro-Will作为正态分布检验的方法，原假设H0:样本符合正态分布。


# 按不同的处理方法，进行分组
> len_VC<-ToothGrowth$len[which(ToothGrowth$supp=='VC')]
> len_OJ<-ToothGrowth$len[which(ToothGrowth$supp=='OJ')]

# 正态分布检验
> shapiro.test(len_VC)

	Shapiro-Wilk normality test

data:  len_VC
W = 0.96567, p-value = 0.4284

# 正态分布检验
> shapiro.test(len_OJ)

	Shapiro-Wilk normality test

data:  len_OJ
W = 0.91784, p-value = 0.02359

两个样本的W统计量都接近1，且p-value都大于0.05，不能拒绝原假设，两组样本数据为正态分布。

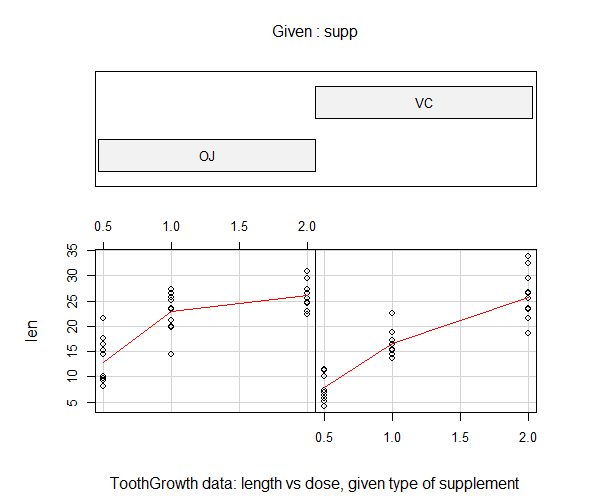
查看数据的相关性。


> coplot(len ~ dose | supp, data = ToothGrowth, panel = panel.smooth,
       xlab = "ToothGrowth data: length vs dose, given type of supplement")

3. F检验实现

3.1 随机数进行F检验
我们先用一种随机数，来做一下F检验。以正态分布生成2组数据，数量，均值，方差都不同，进行F检验。


# 生成随机数
> set.seed(1)
> x <- rnorm(50, mean = 0, sd = 2)
> y <- rnorm(30, mean = 1, sd = 1)

# 进行F检验
> var.test(x, y)

	F test to compare two variances

data:  x and y
F = 2.6522, num df = 49, denom df = 29, p-value
= 0.006232
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 1.332510 4.989832
sample estimates:
ratio of variances 
          2.652168

指标解释：

  • H0:原假设2组样本的方差，无显著差异
  • F统计量：2.6522
  • num df，分子自由度，50-1=49
  • denom df，分每自由度，30-1=29
  • p-value值：0.006232
  • 95 percent confidence interval：95%的置信区间
  • ratio of variances：方差比率2.652168

结果解读，以0.05为显著性水平，F = 2.6522大于临界值1.81(查表)，F值显著，拒绝原假设。以0.05为显著性水平，p-value=0.006232小于0.05，拒绝原假设，两样本方差有显著性差异。这个结果与我们构造的数据是一致的，样本的方差就是不同的。

3.2 ToothGrowth进行F检验
使用ToothGrowth数据集进行F检验，原假设HO，用VC和OJ两种方法按3种剂量进行注射，对于60只豚鼠的牙齿生长速度的方差，没有显著性差异。


> var.test(len_VC,len_OJ)

	F test to compare two variances

data:  len_VC and len_OJ
F = 1.5659, num df = 29, denom df = 29, p-value
= 0.2331
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.745331 3.290028
sample estimates:
ratio of variances 
          1.565937

结果解读，以0.05为显著性水平，F=1.5659小于临界值1.90(查表)，F值不显著，不能拒绝原假设。以0.05为显著性水平，p-value=0.2331大于0.05，不能拒绝原假设，所以两种方法的3种剂量实验的方差，没有显著性的差异。

我们可以用F值进行显著性差异判断，也可以用p值进行显著性差异判断，他们的作用是一样的。F值判断时，需要用计算所得的F值，与显著性水平查表对比。p值相当于是把F值，进行一种标准化的变型，只和已经定义好的显著性水平比就行了，比如0.05, 0.01, 0.001等几个固定值。

手动计算F值和P值，关于P值的详细解释，请查看文章R语言实现统计检验-P值


# 手动计算T值
> Xn<-length(len_VC)
> Yn<-length(len_OJ)
> Xm<-mean(len_VC)
> Ym<-mean(len_OJ)

# 计算两组样本的偏方差
> fx<-sum((len_VC-Xm)^2)/(Xn-1)
> fy<-sum((len_OJ-Ym)^2)/(Yn-1)

# 计算F值
> fx/fy
[1] 1.565937

# 手动计算P值，双边检验
> p_value<-pf(f_stat,Yn-1,Xn-1)
> p_value<-2*min(p_value, 1 - p_value);p_value
[1] 0.2331433

用F检验测试样本数据的偶然误差，对数据集进行方差齐性检验，从而判断数据是否有显著性差异，为方差分析提供了基本的判别方法，对于研究数据的波动性是非常有用的。

转载请注明出处：
http://blog.fens.me/r-test-f

打赏作者