R的极客理想系列文章,涵盖了R的思想,使用,工具,创新等的一系列要点,以我个人的学习和体验去诠释R的强大。
R语言作为统计学一门语言,一直在小众领域闪耀着光芒。直到大数据的爆发,R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入,R语言的社区在迅速扩大成长。现在已不仅仅是统计领域,教育,银行,电商,互联网….都在使用R语言。
要成为有理想的极客,我们不能停留在语法上,要掌握牢固的数学,概率,统计知识,同时还要有创新精神,把R语言发挥到各个领域。让我们一起动起来吧,开始R的极客理想。
关于作者:
- 张丹,分析师/程序员/Quant: R,Java,Nodejs
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-nn-neuralnet/
前言
“神经网络”,“深度学习”,已经不是纯学术的词了,有很多的算法已经落地为我们生活中的各种产品,比如人脸识别,智能客服,从图片中提词,AI作诗,AI作画,chatGPT,AphlaGo等,各种的AI算法应用出圈,打破很多行业壁垒,甚至机器比人类更有创造力,做的更好。这些AI应用出圈的背后,很大程度上是依赖于神经网络的高速发展。
跟上时代的脚步,我将用R语言详细地介绍神经网络建模和应用的过程,以动手操作为主。本文是神经网络的第一篇文章:用R语言10分钟上手神经网络模型neuralnet。
目录
- 神经网络介绍
- neuralnet包介绍
- 神经元模型:零隐藏层
- 单层神经网络(感知机):一个隐藏层
- 单层神经网络:多分类
- 两层神经网络(多层感知器):多分类
- 多层神经网络(深度学习)
1. 神经网络介绍
神经网络,也称为人工神经网络 (ANN) 是机器学习的子集,并且是深度学习算法的核心。其名称和结构是受人类大脑的启发,模仿了生物神经元信号相互传递的方式。
人工神经网络 (ANN) 由节点层组成,包含一个输入层、一个或多个隐藏层和一个输出层。 每个节点也称为一个人工神经元,它们连接到另一个节点,具有相关的权重和阈值。 如果任何单个节点的输出高于指定的阈值,那么该节点将被激活,并将数据发送到网络的下一层。 否则,不会将数据传递到网络的下一层。
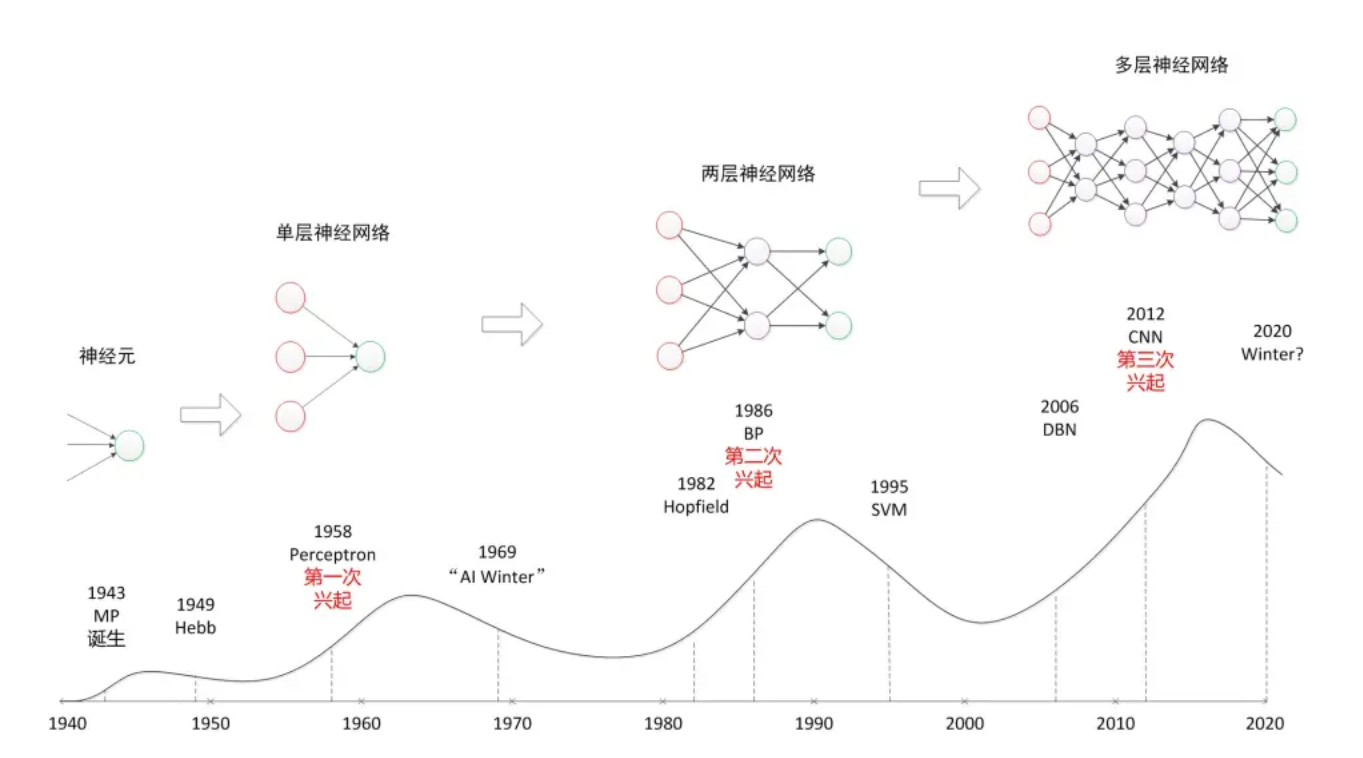
从单层神经网络(感知器)开始,到包含一个隐藏层的两层神经网络,再到多层的深度神经网络,一共有三次兴起过程。
在神经网络中,处理单元通常按层次分布于神经网络的输入层、隐层和输出层中,因此分别称之为输入节点、隐节点和输出节点,各自的功能如下所示:
- 输入节点:接受与处理训练数据集中的各输入变量值
- 隐藏点:实现非线性数据的线性变换
- 输出节点:给出输出变量的分类或预测结果
2. neuralnet包介绍
在R语言里面,有好几个包都支持神经网络模型,neuralnet包就一个常用包。
neuralnet包,安装过程很简单。
# 安装
> install.packages("neuralnet")
# 加载
> library(neuralnet)
# 设置工作路径
> setwd("C:/work/R/neural/neural_networks")
neuralnet包中的,neuralnet()函数可用于神经网络的模型训练,是这个包中最核心的函数,neuralnet()函数参数很多,是需要我们仔细了解的。
neuralnet()函数,在训练神经网络模型时,支持使用反向传播(BP)、弹性反向传播(RPROP)、无权重回溯、修正的全球收敛版本(GRPROP)训练神经网络,函数允许通过自定义选择误差和激活函数进行灵活设置。此外,还实现了广义权重的计算。
查看neuralnet()函数
> neuralnet
function (formula, data, hidden = 1, threshold = 0.01, stepmax = 1e+05,
rep = 1, startweights = NULL, learningrate.limit = NULL,
learningrate.factor = list(minus = 0.5, plus = 1.2), learningrate = NULL,
lifesign = "none", lifesign.step = 1000, algorithm = "rprop+",
err.fct = "sse", act.fct = "logistic", linear.output = TRUE,
exclude = NULL, constant.weights = NULL, likelihood = FALSE)
...
参数列表:
- formula: 定义模型的公式。
- data: data.frame格式,训练集原始数据。
- hidden: 整数向量,指定每层中隐藏神经元的数量,如c(3,2)为二个隐藏层,第一层3个节点,第二层2个节点。
- threshold: 数值型,停止条件阈值,指定误差函数的偏导数作为停止标准的阈值。
- stepmax: 数值型,停止条件最大迭代次数,达到这个最大值就会停止神经网络的训练过程。
- rep: 神经网络训练的重复次数。
- startweights: 模型起始值的权重向量,设置为NULL用于随机初始化。
- learningrate.limit: 一个向量或一个列表,包含学习率的最低和最高限制,仅用于RPROP和GRPROP。
- learningrate.factor: 一个向量或一个列表,包含学习率的上限和下限的乘法系数,仅用于RPROP和GRPROP。
- learningrate: 数值型,指定传统反向传播使用的学习率,只用于传统的反向传播。
- lifesign: 字符串,指定函数在计算神经网络时的打印量,’none’, ‘minimal’ or ‘full’。
- lifesign.step: 整数型,指定在完全lifesign模式下打印最小阈值的步长。
- algorithm: 字符串,包含用于计算神经网络的算法类型。以下类型是可能的:”backprop”,”rprop+”,”rprop-“,”sag”,或 “slr”。backprop’指的是反向传播,’rprop+’和’rprop-‘指的是带有和不带有权重回溯的弹性反向传播,而’sag’和’slr’则是诱导使用修改后的全局收敛算法(GRPROP)。
- err.fct: 损失函数,用于计算误差的函数,可以使用字符串’sse’和’ce’,它们代表平方误差之和和交叉熵。
- act.fct: 激活函数,用于平滑协变量或神经元与权重的交叉积的结果。字符串 “logistic”和 “tanh” 可以用于logistic函数和切线双曲。
- linear.output:逻辑值,是否线性输出,即是回归还是分类。TRUE表示输出节点的激活函数为线性函数,FALSE表示非线性函数,在B-P中为FALSE
- exclude: 一个向量或一个矩阵,指定从计算中排除的权重。如果给定的是一个向量,必须知道权重的确切位置。一个有n行3列的矩阵将排除n个权重,其中第一列代表层,第二列代表输入神经元,第三列代表权重的输出神经元。
- constant.weights: 一个向量,指定训练过程中不需要训练的权重,固定值。
- likelihood: 逻辑值,如果误差函数等于负对数似然函数,将计算信息准则AIC和BIC。
在实际建模过程中,我们主要使用formula,data,hidden,threshold,algorithm,err.fct,act.fct,linear.output这个参数。
3. 神经元模型:零隐藏层
我们先建立一个最简单的网络模型,只有输入节点和输出节点,不包括隐藏层。这种结构都不算是神经网络,是神经网络的前身神经元模型。神经元模型是一个包含输入,输出与计算功能的模型。输入可以类比为神经元的树突,而输出可以类比为神经元的轴突,计算则可以类比为细胞核。
查看iris数据集
> head(iris)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
6 5.4 3.9 1.7 0.4 setosa
以iris数据集的全量数据做为输入,对单一目标Species==”setosa”,做二分类的模型,判断是否属于是setosa的种类。
# 没有隐藏层
> nn <- neuralnet(Species=="setosa"~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width,
+ data = iris,hidden = 0)
# 查看网络结构
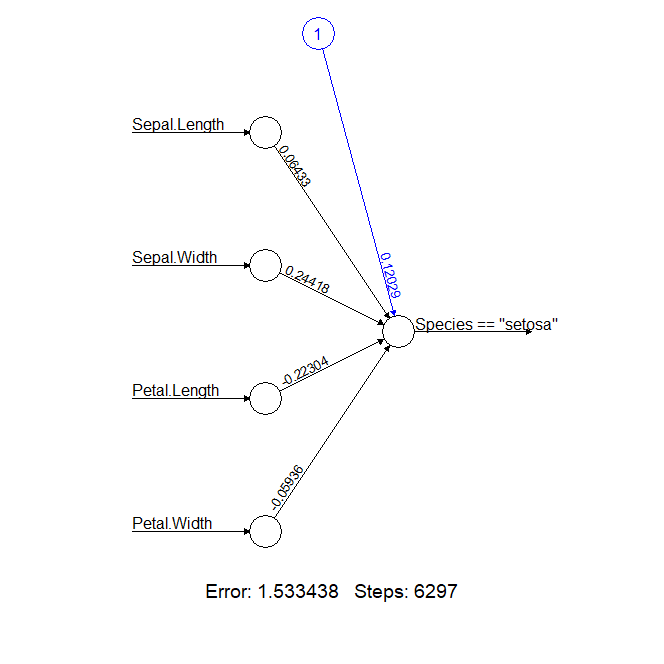
> plot(nn)
从输出的神经网络结构图中,我们可以看到,四个输入节点为iris数据集的4个参数(Sepal.Length Sepal.Width Petal.Length Petal.Width Species),输出节点(Species)为模型训练目标,蓝色节点1为这一层的偏差权重(截距)值,从输入节点到输出节点的连线上,有权重值。我们训练神经网络模型,就是为了算出这些权重值,反复迭代。
接下来,我们查看模型的各种输出结果,都在nn这个对象中。
- call:模型函数
- response:因变量数据
- covariate:自变量数据
- model.list:模型函数
- err.fct:损失函数
- act.fct:激活函数
- linear.output:是否线性输出
- data:原始数据集
- exclude:指定从计算中排除的权重
- net.result:预测值结果
- weights:各个节点的权重值列表
- generalized.weights:广义权重
- startweights:各个节点的初始权重(初始权值为在的正态分布随机数)
- result.matrix:结果矩阵,终止迭代时各个节点的权重,迭代次数,损失函数值和权重的最大调整量
首先,来查看结果矩阵result.matrix。
> nn$result.matrix
[,1]
error 1.533438e+00
reached.threshold 9.212915e-03
steps 6.297000e+03
Intercept.to.Species == "setosa" 1.202943e-01
Sepal.Length.to.Species == "setosa" 6.432600e-02
Sepal.Width.to.Species == "setosa" 2.441786e-01
Petal.Length.to.Species == "setosa" -2.230368e-01
Petal.Width.to.Species == "setosa" -5.935682e-02
- error,损失函数值,1.533438,值越小
- reached.threshold,终止条件,权重的最大调整量9.212915e-03
- steps,整个训练执行了6297步
- Intercept.to.Species,偏差权重(截距),值为1.202943e-01
- Sepal.Length.to.Species,Sepal.Length变量权重
- Sepal.Width.to.Species,Sepal.Width变量权重
- Petal.Length.to.Species,Petal.Length变量权重
- Petal.Width.to.Species,Petal.Width变量权重
查看连接的初始的权重,随机分配的,分别对应5个不同输入节点到输出节点的权重。
> nn$startweights
[[1]]
[[1]][[1]]
[,1]
[1,] 0.5797599
[2,] -0.3526484
[3,] 1.7074446
[4,] 1.3395568
[5,] 0.7781903
查看模型最终的连接权重列表,从startweights初始到weights最终结果。
> nn$weights
[[1]]
[[1]][[1]]
[,1]
[1,] 0.12029435
[2,] 0.06432600
[3,] 0.24417858
[4,] -0.22303683
[5,] -0.05935682
查看模型中的广义权重,分别对应每个样本数据的权重值
# 取前6条
> head(nn$generalized.weights[[1]])
[,1] [,2] [,3] [,4]
[1,] 3.1084343 11.799476 -10.777840 -2.8683080
[2,] 0.4883183 1.853634 -1.693141 -0.4505957
[3,] 0.7288879 2.766825 -2.527265 -0.6725814
[4,] 0.4490363 1.704522 -1.556939 -0.4143483
[5,] 20.4485892 77.621919 -70.901170 -18.8689374
[6,] -3.7104548 -14.084718 12.865219 3.4238224
查看模型的计算函数
# 模型公式
> nn$call
neuralnet(formula = Species == "setosa" ~ Sepal.Length + Sepal.Width +
Petal.Length + Petal.Width, data = iris, hidden = 0)
# 损失函数
> nn$err.fct
function (x, y)
{
1/2 * (y - x)^2
}
attr(,"type")
[1] "sse"
# 激活函数
> nn$act.fct
function (x)
{
1/(1 + exp(-x))
}
attr(,"type")
[1] "logistic"
查看模型的变量
# 模型的变量定义
> nn$model.list
$response
[1] "Species == \"setosa\""
$variables
[1] "Sepal.Length" "Sepal.Width" "Petal.Length" "Petal.Width"
# 查看自变量,取前6条
> head(nn$covariate)
Sepal.Length Sepal.Width Petal.Length Petal.Width
[1,] 5.1 3.5 1.4 0.2
[2,] 4.9 3.0 1.4 0.2
[3,] 4.7 3.2 1.3 0.2
[4,] 4.6 3.1 1.5 0.2
[5,] 5.0 3.6 1.4 0.2
[6,] 5.4 3.9 1.7 0.4
查看因变量的实际值,对模型预测输出变量的预测概率值。
# 查看因变量,实际值,取前6条
> head(nn$response)
Species == "setosa"
1 TRUE
2 TRUE
3 TRUE
4 TRUE
5 TRUE
6 TRUE
# 模型预测结果,取前6条
> head(nn$net.result[[1]])
[,1]
[1,] 0.9788590
[2,] 0.8439046
[3,] 0.9021788
[4,] 0.8267209
[5,] 0.9968443
[6,] 1.0170459
通过建立一个最简单的网络模型,我们就能了解 neuralnet() 函数的是怎么使用的了,涉及到的内容还是很多的。对于零隐藏层的网络而言,就可以理解为一个线性模型。
4. 单层神经网络(感知机):一个隐藏层
接下来,我们建立一个真正的神经网络模型,包括输入节点、输出节点、1个隐藏层节,还是以iris数据集的全量数据做为输入,对单一目标Species==”setosa”,做二分类的模型,判断是否属于是setosa的种类。
代码只是改动一处,让hidden=1。
# 训练
> n1 <- neuralnet(Species=="setosa"~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width,
+ data = iris,hidden=1)
# 画出网络结构
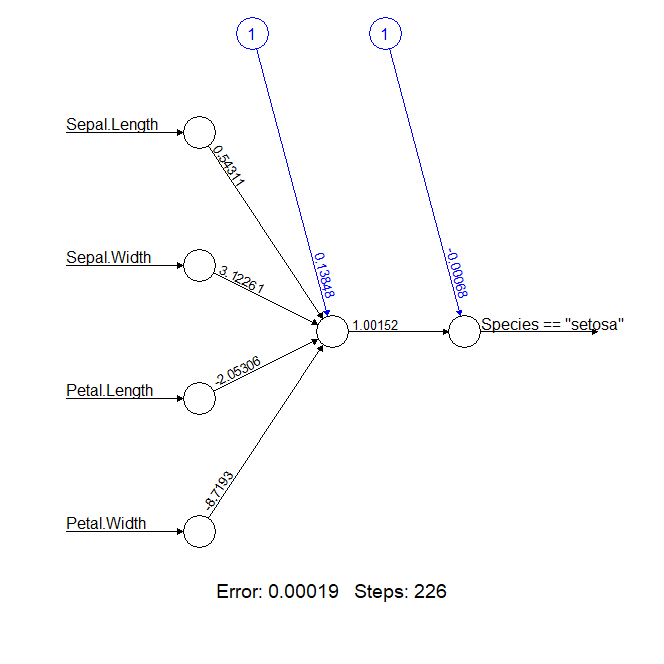
> plot(n1)
查看结果矩阵
> n1$result.matrix
[,1]
error 1.899890e-04
reached.threshold 9.246323e-03
steps 2.260000e+02
Intercept.to.1layhid1 1.384797e-01
Sepal.Length.to.1layhid1 5.431059e-01
Sepal.Width.to.1layhid1 3.122608e+00
Petal.Length.to.1layhid1 -2.053056e+00
Petal.Width.to.1layhid1 -8.719302e+00
Intercept.to.Species == "setosa" -6.759521e-04
1layhid1.to.Species == "setosa" 1.001522e+00
error的损失值为0.00019,整个训练执行了226步,比神经元模型的零隐藏层,有了大幅的提升。一下子就把分类问题解决了,太神奇了吧。
5. 单层神经网络:多分类
我们增加点难度,用单层神经网路,做个多分类的。
# 单层网络
> n2a <- neuralnet(Species~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width,
+ data = iris,hidden=1)
# 画图
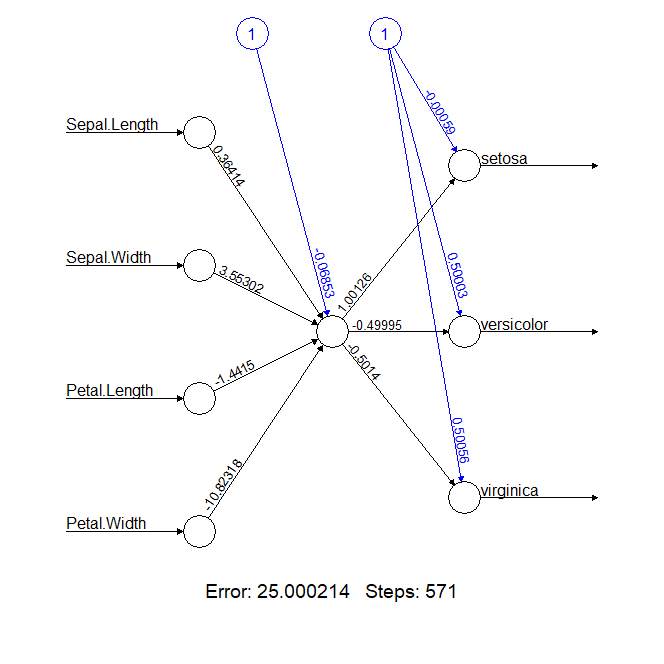
> plot(n2a)
从网络结构看,输出为4个节点,隐藏层为一个节点,输出3个节点,为3类。输出结果惨不忍睹,error竟然达到了25,基本都是错了。
接下来,我们试试增加隐藏层节点数,从1个变成2个,看看做个多分类的效果。
# 单层网络,2个节点
> n2b <- neuralnet(Species~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width,
+ data = iris,hidden=c(2))
> plot(n2b)
从网络结构看,输出为4个节点,隐藏层为两个节点,输出3个节点,为3类。输出结果一下就不错了,error为1.9,步骤是15981,这个结果是能用的。
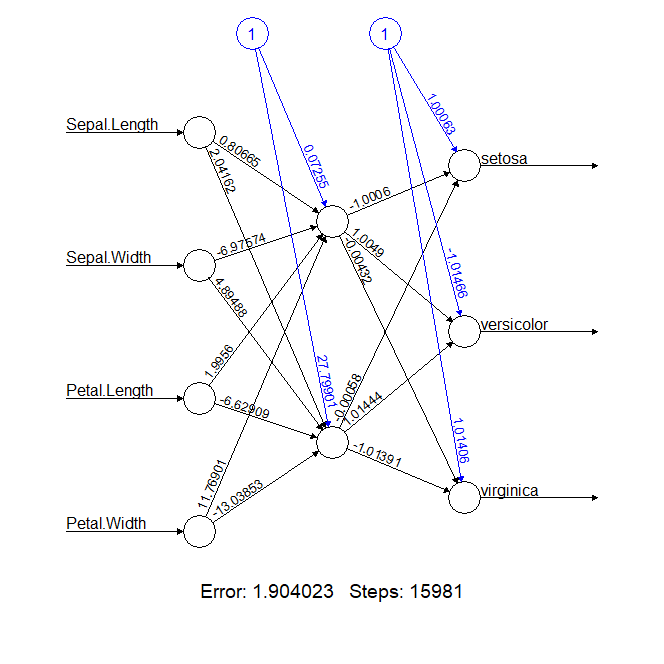
由于一层神经网络的感知器也只能做线性分类任务,在10年后,才对于两层神经网络的研究才带来神经网络的复苏。
6. 两层神经网络(多层感知器):多分类
下面我们要建立一个两层神经网络模型,包括输入层、输出层、2个隐藏层,还是以iris数据集的全量数据做为输入,对单一目标Species做三分类的模型。
首先,先尝2个隐藏层,每层一个节点,试试模型效果。
# 2个隐藏层,每层1个节点
> n3a <- neuralnet(Species~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width, + data = iris,hidden=c(1,1)) > n3a$result.matrix
[,1]
error 25.000112366
reached.threshold 0.007309118
steps 358.000000000
Intercept.to.1layhid1 2.677698687
Sepal.Length.to.1layhid1 -0.737245035
Sepal.Width.to.1layhid1 3.844506938
Petal.Length.to.1layhid1 -1.018677154
Petal.Width.to.1layhid1 -10.512582993
Intercept.to.2layhid1 -0.771711595
1layhid1.to.2layhid1 3.469423693
Intercept.to.setosa -0.510039484
2layhid1.to.setosa 1.612291660
Intercept.to.versicolor 0.754101331
2layhid1.to.versicolor -0.804506879
Intercept.to.virginica 0.755525924
2layhid1.to.virginica -0.807147653
error达到了25,又是一个不可接受的结果。
在层数不变的情况下,继续增加每层的节点数,调整为每个隐藏层2个节点。从结果矩阵看,多个很多参数的输出,这些节点都是有神经网络自动生成了,也就是不可解释的因素。
# 2个隐藏层,每层2个节点
> n3b <- neuralnet(Species~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width, + data = iris,hidden=c(2,2)) # 结果矩阵 > n3b$result.matrix
[,1]
error 24.999473404
reached.threshold 0.008004802
steps 83.000000000
Intercept.to.1layhid1 -0.493094700
Sepal.Length.to.1layhid1 -1.519304930
Sepal.Width.to.1layhid1 -1.217278013
Petal.Length.to.1layhid1 3.491582287
Petal.Width.to.1layhid1 3.469063900
Intercept.to.1layhid2 -0.921659140
Sepal.Length.to.1layhid2 -2.263419044
Sepal.Width.to.1layhid2 0.410851516
Petal.Length.to.1layhid2 1.581399076
Petal.Width.to.1layhid2 -1.453986728
Intercept.to.2layhid1 0.898644804
1layhid1.to.2layhid1 -2.635824185
1layhid2.to.2layhid1 -2.577338580
Intercept.to.2layhid2 -0.829242612
1layhid1.to.2layhid2 -0.706157301
1layhid2.to.2layhid2 1.549670915
Intercept.to.setosa -0.436567651
2layhid1.to.setosa 1.527644298
2layhid2.to.setosa 1.165157296
Intercept.to.versicolor 0.374083691
2layhid1.to.versicolor -1.298521851
2layhid2.to.versicolor 1.805614407
Intercept.to.virginica 0.455763243
2layhid1.to.virginica -1.181002787
2layhid2.to.virginica 1.253298145
# 画图
> plot(n3b)
下来的操作,就是继续加节点。在层数不变的情况下,继续增加每层的节点数,调整为每个隐藏层3个节点。
# 2个隐藏层,每层3个节点
> n3c <- neuralnet(Species~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width, + data = iris,hidden=c(3,3)) > n3c$result.matrix
[,1]
error 9.861760e-01
reached.threshold 9.760993e-03
steps 1.842800e+04
Intercept.to.1layhid1 7.178501e-01
Sepal.Length.to.1layhid1 2.725448e-01
Sepal.Width.to.1layhid1 1.376482e+00
Petal.Length.to.1layhid1 -1.262652e+00
Petal.Width.to.1layhid1 -1.997635e+00
Intercept.to.1layhid2 -2.753156e+00
Sepal.Length.to.1layhid2 -1.465864e+00
Sepal.Width.to.1layhid2 4.125512e+00
Petal.Length.to.1layhid2 -6.026538e-01
Petal.Width.to.1layhid2 2.743376e+00
Intercept.to.1layhid3 1.379399e+00
Sepal.Length.to.1layhid3 -2.256887e-01
Sepal.Width.to.1layhid3 1.027688e+00
Petal.Length.to.1layhid3 3.221391e-01
Petal.Width.to.1layhid3 -2.847147e+00
Intercept.to.2layhid1 -2.353385e+00
1layhid1.to.2layhid1 -1.315389e+03
1layhid2.to.2layhid1 3.555585e+01
1layhid3.to.2layhid1 6.903238e+01
Intercept.to.2layhid2 -6.702997e-01
1layhid1.to.2layhid2 1.352140e+00
1layhid2.to.2layhid2 -5.184099e-02
1layhid3.to.2layhid2 -2.994567e-01
Intercept.to.2layhid3 -3.106167e+00
1layhid1.to.2layhid3 4.958443e+00
1layhid2.to.2layhid3 -2.185125e-01
1layhid3.to.2layhid3 -1.677417e+00
Intercept.to.setosa 4.026726e-01
2layhid1.to.setosa -1.575905e-02
2layhid2.to.setosa -1.461912e+00
2layhid3.to.setosa 2.965282e+00
Intercept.to.versicolor 6.790011e-01
2layhid1.to.versicolor -9.706799e-01
2layhid2.to.versicolor 1.210438e+00
2layhid3.to.versicolor -2.833834e+00
Intercept.to.virginica -2.389590e-01
2layhid1.to.virginica 9.950653e-01
2layhid2.to.virginica 7.442383e-01
2layhid3.to.virginica -3.957608e-01
# 画图
> plot(n3c)
瞬间,模型效果又达到了惊人的新高度,error为0.986,只能用神奇来形容,我也不知道为什么,算法的“玄学” 由此而来。

7. 多层神经网络(深度学习):多个隐藏层
在上个步骤中,我们是层数不变增加每层节点数,当然我们也可以节点数不变,增加更多的层数来操作。继续增加到3层的,保持节点数每个隐藏层2个节点进行测试。
# 3个隐藏层,每层2个节点
> n3d <- neuralnet(Species~ Sepal.Length + Sepal.Width + Petal.Length +
Petal.Width, + data = iris,hidden=c(2,2,2))
# 结果矩阵
> n3d$result.matrix
[,1]
error 9.814611e-01
reached.threshold 9.856631e-03
steps 2.599500e+04
Intercept.to.1layhid1 4.377454e+00
Sepal.Length.to.1layhid1 2.988690e+00
Sepal.Width.to.1layhid1 4.895009e+00
Petal.Length.to.1layhid1 4.739920e+00
Petal.Width.to.1layhid1 5.049575e+00
Intercept.to.1layhid2 1.713367e+00
Sepal.Length.to.1layhid2 4.900288e-01
Sepal.Width.to.1layhid2 6.486628e-01
Petal.Length.to.1layhid2 -1.317743e+00
Petal.Width.to.1layhid2 -1.286672e+00
Intercept.to.2layhid1 -5.678148e+01
1layhid1.to.2layhid1 -5.584444e+01
1layhid2.to.2layhid1 9.250502e+02
Intercept.to.2layhid2 1.417653e+01
1layhid1.to.2layhid2 1.370346e+01
1layhid2.to.2layhid2 -3.770254e+01
Intercept.to.3layhid1 -1.702465e+00
2layhid1.to.3layhid1 1.833016e+00
2layhid2.to.3layhid1 4.370202e+00
Intercept.to.3layhid2 -2.525917e+00
2layhid1.to.3layhid2 8.186075e+00
2layhid2.to.3layhid2 1.849959e+00
Intercept.to.setosa 1.991064e+00
3layhid1.to.setosa -2.193503e+00
3layhid2.to.setosa 1.780463e-01
Intercept.to.versicolor -2.462871e+00
3layhid1.to.versicolor 2.184454e+00
3layhid2.to.versicolor 1.303726e+00
Intercept.to.virginica 1.471821e+00
3layhid1.to.virginica 9.088568e-03
3layhid2.to.virginica -1.481810e+00
# 画图
> plot(n3d)
三个隐藏的模型效果,同样能达到非常好的效果,error为0.981。
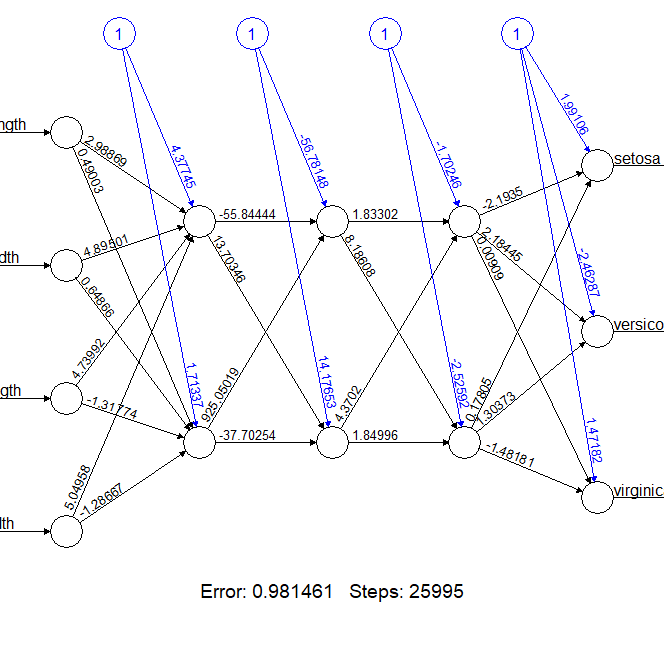
通过不停的增加层数的节点数,神经网络模型会越来越好,但是计算的复杂度会越来越高,从结果矩阵的输出,我们就可感觉到,输出的变量一次比一次多,都不知道这些变量是干什么用的,要想去解释这个模型根本就无从下手。
保持理性的思维,虽然神经网络可以无限帮我们提升模型的效果,但由于不可以解释,“玄之又玄”,需要在适合场景来使用,而不是全都交给神经网络。本文为神经网络的入门文章第一篇,针对这个主题,我们也准备多写几篇文章,来用R语言进行详细的描述。
说多少理论都不如上手一试。本文代码已上传到github: https://github.com/bsspirit/neural_networks/blob/main/01_neuralnet.r
转载请注明出处:
http://blog.fens.me/r-nn-neuralnet/