R的极客理想系列文章,涵盖了R的思想,使用,工具,创新等的一系列要点,以我个人的学习和体验去诠释R的强大。
R语言作为统计学一门语言,一直在小众领域闪耀着光芒。直到大数据的爆发,R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入,R语言的社区在迅速扩大成长。现在已不仅仅是统计领域,教育,银行,电商,互联网….都在使用R语言。
要成为有理想的极客,我们不能停留在语法上,要掌握牢固的数学,概率,统计知识,同时还要有创新精神,把R语言发挥到各个领域。让我们一起动起来吧,开始R的极客理想。
关于作者:
- 张丹,分析师/程序员/Quant: R,Java,Nodejs
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-bit-operation/
前言
本来是要研究字符串的匹配的问题,然后看着看着就到了文本距离的计算,然后就又到了位运算。要不然也不会想到,用R语言搞二进制的位运算研究。每种算法一旦刨根问底,都是会到计算机的底层计算逻辑。
赶上了问题,就认真面对问题,把二进制和位运算一些看看。关于进制转换的文章,请参考用R语言进制转换-二进制八进制十六进制
目录
- 什么是位运算
- 位运算的计算过程
- R语言中的位运算
1. 什么是位运算
计算机中的所有数值,都是在内存中都是以二进制的形式储存的,即 0、1 两种状态。位运算就是直接对内存中的二进制位数据进行的操作。比如,“&”与运算是一个逻辑运算符,6的二进制是110,11的二进制是1011,那么6 & 11的结果就是2,它是二进制对应位进行逻辑运算的结果(0表示False,1表示True,空位都当0处理)。
位运算概览:
| 符号 | 描述 | 运算规则 |
| & | 与 | 两个位都为1时,结果才为1 |
| | | 或 | 两个位都为0时,结果才为0 |
| xor | 异或 | 两个位相同为0,相异为1 |
| ~ | 取反 | 0变1,1变0 |
| << | 左移 | 各二进位全部左移若干位,高位丢弃,低位补0 |
| >> | 右移 | 各二进位全部右移若干位,对无符号数,高位补0,有符号数,各编译器处理方法不一样,有的补符号位(算术右移),有的补0(逻辑右移) |
2. 位运算的计算过程
2.1 按位与(&)
定义:参加运算的两个数据,按二进制位进行”与”运算。
运算规则:两位同时为1,结果才为1,否则结果为0。
0&0=0 , 0&1=0, 1&0=0, 1&1=1举例说明:
(3)₁₀ & (5)₁₀ = (00000011)₂ & (00000101)₂ = (00000001)₂ = (1)₁₀
| 操作 | 十进制 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |
| & | 5 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| = | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
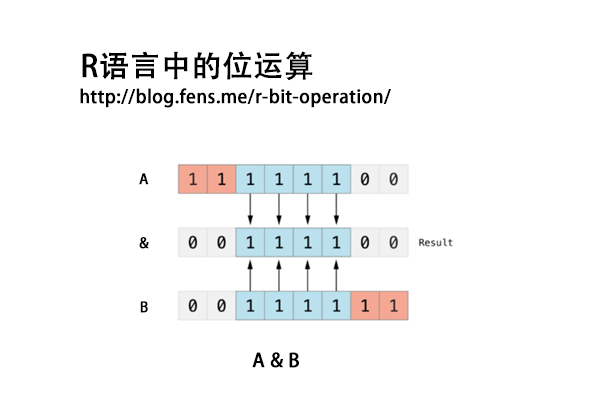
(23)₁₀ & (15)₁₀ = (00010111)₂ & (00001111)₂ = (00000111)₂ = (7)₁₀
| 操作 | 十进制 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 23 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | |
| & | 15 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| = | 7 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
与运算的用途:
1)清零
如果想将一个单元清零,即使其全部二进制位为0,只要与一个各位都为零的数值相与,结果为零。
2)取一个数的指定位
比如取数 X=1010 1110 的低4位,只需要另找一个数Y,令Y的低4位为1,其余位为0,即Y=0000 1111,然后将X与Y进行按位与运算(X&Y=0000 1110)即可得到X的指定位。
3)判断奇偶
只要根据最未位是0还是1来决定,为0就是偶数,为1就是奇数。因此可以用if ((a & 1) == 0)代替if (a % 2 == 0)来判断a是不是偶数。
2.2 按位或(|)
定义:参加运算的两个对象,按二进制位进行”或”运算。
运算规则:参加运算的两个对象只要有一个为1,其值为1。
0|0=0, 0|1=1, 1|0=1, 1|1=1举例说明:
(3)₁₀ | (5)₁₀ = (00000011)₂ | (00000101)₂ = (00000111)₂ = (7)₁₀
| 操作 | 十进制 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |
| | | 5 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| = | 7 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
(23)₁₀ | (15)₁₀ = (00010111)₂ | (00001111)₂ = (00011111)₂ = (31)₁₀
| 操作 | 十进制 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 23 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | |
| | | 15 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| = | 31 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
注意:负数按补码形式参加按位或运算。
或运算的用途:
1)常用来对一个数据的某些位设置为1
比如将数 X=1010 1110 的低4位设置为1,只需要另找一个数Y,令Y的低4位为1,其余位为0,即Y=0000 1111,然后将X与Y进行按位或运算(X|Y=1010 1111)即可得到。
2.3 按位异或(xor)
定义:参加运算的两个数据,按二进制位进行”异或”运算。
运算规则:参加运算的两个对象,如果两个相应位相同为0,相异为1。
0 xor 0=0, 0 xor 1=1, 1 xor 0=1, 1 xor 1=0举例说明:
(3)₁₀ xor (5)₁₀ = (00000011)₂ xor (00000101)₂ = (00000111)₂ = (7)₁₀
| 操作 | 十进制 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |
| xor | 5 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| = | 6 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
(23)₁₀ xor (15)₁₀ = (00010111)₂ xor (00001111)₂ = (00011000)₂ = (24)₁₀
| 操作 | 十进制 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 23 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | |
| xor | 15 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| = | 24 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
异或的几条性质:
- 交换律 (a xor b) == (b xor a)
- 结合律 (a xor b) xor c == a xor (b xor c)
- 对于任何数x,都有 x xor x=0,x xor 0=x
- 自反性: a xor b xor b = a xor 0=a
异或运算的用途:
1)翻转指定位
比如将数 X=1010 1110 的低4位进行翻转,只需要另找一个数Y,令Y的低4位为1,其余位为0,即Y=0000 1111,然后将X与Y进行异或运算(X xor Y=1010 0001)即可得到。
2)与0相异或值不变
例如:(10101110)₂ xor (00000000)₂ = (10101110)₂
2.4 按位非(~)
定义:参加运算的一个数据,按二进制进行”取反”运算。
运算规则: 对一个二进制数按位取反,即将0变1,1变0。
~1=0, ~0=1举例说明:
~ (3)₁₀ = ~(00000011)₂ = (11111100)₂ = (-4)₁₀
| 操作 | 十进制 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ~ | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| = | -4 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
~(23)₁₀ = ~(00010111)₂ = (11101000)₂ = (-24)₁₀
| 操作 | 十进制 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ~ | 23 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| = | -24 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
按位非运算的用途:
1)使一个数的最低位为零
使a的最低位为0,可以表示为:a & ~1。~1的值为 1111 1111 1111 1110,再按”与”运算,最低位一定为0。因为” ~”运算符的优先级比算术运算符、关系运算符、逻辑运算符和其他运算符都高。
2.5 按位左移(<<)
定义:将一个运算对象的各二进制位全部左移若干位(左边的二进制位丢弃,右边补0)。
设 a=1010 1110,a = a<< 2 将a的二进制位左移2位、右补0,即得a=1011 1000。
若左移时舍弃的高位不包含1,则每左移一位,相当于该数乘以2。
举例说明:
(3)₁₀<< 1= (00000011)₂ << (1)₁₀= (00000110)₂ = (6)₁₀
| 操作 | 十进制 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |
| << | 1 | ||||||||
| = | 6 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
(3)₁₀<< 2= (00000011)₂ << (2)₁₀ = (00001100)₂ = (12)₁₀
| 操作 | 十进制 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | |
| << | 2 | ||||||||
| = | 12 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
2.6 按位右移(>>)
定义:将一个数的各二进制位全部右移若干位,正数左补0,负数左补1,右边丢弃。
例如:a=a>>2 将a的二进制位右移2位,左补0 或者 左补1得看被移数是正还是负。
操作数每右移一位,相当于该数除以2。
举例说明:
(30)₁₀>> 1= (00011110)₂ << (1)₁₀= (00001111)₂ = (15)₁₀
| 操作 | 十进制 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 30 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | |
| >> | 1 | ||||||||
| = | 15 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
(30)₁₀>> 4= (00011110)₂ << (4)₁₀ = (00000001)₂ = (1)₁₀
| 操作 | 十进制 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | |
| >> | 4 | ||||||||
| = | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
3. R语言中的位运算
R语言位运算操作概览:
| 操作函数 | 描述 | 语法 |
| bitwAnd | 按位与(&) | bitwAnd(value1,value2) |
| bitwOr | 按位或 (|) | bitwOr(value1,value2) |
| bitwXor | 按位异或(XOR) | bitwXor(value1,value2) |
| bitWnot | 按位非(~) | bitwNot(value) |
| bitwShiftL | 左移 | bitwShiftL(value,n) |
| bitwShiftR | 右移 | bitShiftR(value,n) |
位运算的6个操作,对应上文中的位运算的计算过程。
为了方便查看二进制的结果,我写了intToBitString()函数,方便对十进制转二进制阅读。
# 十进制转二进制,默认截取8位
> intToBitString<-function(num,size=8){
+ a<-as.integer(intToBits(num))
+ pos<-max(which(a==1),8)
+ a<-a[1:pos]
+ paste(rev(a), collapse = "")
+ }
把十进制转二进制。
# 把30转二进制
> intToBitString(30)
[1] "00011110"
# 使用默认函数
> intToBits(30)
[1] 00 01 01 01 01 00 00 00 00 00 00 00 00 00 00 00 00 00 00
[20] 00 00 00 00 00 00 00 00 00 00 00 00 00
按位与操作,计算 3 & 5, 23 & 15
> bitwAnd(3,5)
[1] 1
> bitwAnd(23,15)
[1] 7
# 查看二进制数
> intToBitString(3)
[1] "00000011"
> intToBitString(5)
[1] "00000101"
intToBitString(23)
[1] "00010111"
> intToBitString(15)
[1] "00001111"
按位或操作,计算 3 | 5, 23 | 15
> bitwOr(3,5)
[1] 7
> bitwOr(23,15)
[1] 31
按位异或,计算 3 xor 5, 23 xor 15
> bitwXor(3,5)
[1] 6
> bitwXor(23,15)
[1] 24
按位非,计算 ~3 , ~23
> bitwNot(3)
[1] -4
> bitwNot(23)
[1] -24
# 查看-4 和 -24的二进制
> intToBitString(-4)
[1] "11111111111111111111111111111100"
> intToBitString(-24)
[1] "11111111111111111111111111101000"
左移,计算 3<<1 , 3<<2
> bitwShiftL(3,1)
[1] 6
> bitwShiftL(3,2)
[1] 12
# 查看3, 6, 12的二进制
> intToBitString(3)
[1] "00000011"
> intToBitString(6)
[1] "00000110"
> intToBitString(12)
[1] "00001100"
右移,计算 30>>1 , 30>>4
> bitwShiftR(30,1)
[1] 15
> bitwShiftR(30,4)
[1] 1
# 查看30,15,1的二进制
> intToBitString(30)
[1] "00011110"
> intToBitString(15)
[1] "00001111"
> intToBitString(1)
[1] "00000001"
用R实现二进制计算,比原本想象的容易不少,代码不仅简单,而且计算函数功能明确,又get到了新的知识。
转载请注明出处:
http://blog.fens.me/r-bit-operation/