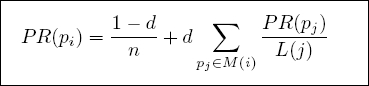Hadoop家族系列文章,主要介绍Hadoop家族产品,常用的项目包括Hadoop, Hive, Pig, HBase, Sqoop, Mahout, Zookeeper, Avro, Ambari, Chukwa,新增加的项目包括,YARN, Hcatalog, Oozie, Cassandra, Hama, Whirr, Flume, Bigtop, Crunch, Hue等。
从2011年开始,中国进入大数据风起云涌的时代,以Hadoop为代表的家族软件,占据了大数据处理的广阔地盘。开源界及厂商,所有数据软件,无一不向Hadoop靠拢。Hadoop也从小众的高富帅领域,变成了大数据开发的标准。在Hadoop原有技术基础之上,出现了Hadoop家族产品,通过“大数据”概念不断创新,推出科技进步。
作为IT界的开发人员,我们也要跟上节奏,抓住机遇,跟着Hadoop一起雄起!
关于作者:
- 张丹(Conan), 程序员Java,R,PHP,Javascript
- weibo:@Conan_Z
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/hadoop-social-peoplerank/
前言
如果说Google改变了互联网,那么社交网络就改变人们的生活方式。通过社交网络,我们每个个体,都是成为了网络的中心。我们的生活半径,被无限放大,通过6个朋友关系,就可以认识世界上任何一个人。
未来的互联网将是属于我们每一个人。
目录
- PeopleRank和PageRank
- 需求分析:从社交网络中发现个体价值
- 算法模型:PeopleRank算法
- 架构设计:PeopleRank计算引擎系统架构
- 程序开发:PeopleRank算法实现
1. PeopleRank和PageRank
PageRank让Google成为搜索领域的No.1,也是当今最有影响力的互联网公司之一,用技术创新改变人们的生活。PageRank主要用于网页评分计算,把互联网上的所有网页都进行打分,给网页价值的体现。
自2012以来,中国开始进入社交网络的时代,开心网,人人网,新浪微博,腾讯微博,微信等社交网络应用,开始进入大家的生活。最早是由“抢车位”,“偷菜”等社交游戏带动的社交网络的兴起,如今人们会更多的利用社交网络,获取信息和分享信息。我们的互联网,正在从以网页信息为核心的网络,向着以人为核心的网络转变着。
于是有人就提出了,把PageRank模型应用于社交网络,定义以人为核心的个体价值。这样PageRank模型就有了新的应用领域,同时也有了一个新的名字PeopleRank。
关于PageRank的介绍,请参考文章:PageRank算法R语言实现
注:PeopleRank网上还有不同的解释,我这里仅仅表示用来解释“PageRank模型”。
下面我们将从一个PeopleRank的案例来解释,如何从社交网络中发现个体价值。
2. 需求分析:从社交网络中发现个体价值
案例介绍:
以新浪微博为例,给微博中每个用户进行评分!
从新浪微博上,把我们的关注和粉丝的关系都找到。
如下图:我在微博上,随便找了几个微博账号。
我们的任务是,需要给这些账号评分!
- 方法一,简单求和:评分=关注数+粉丝数+微博数
- 方法二,加权求和:评分=a*关注数+b*粉丝数+c*微博数
新建数据文件:weibo.csv
~ vi weibo.csv
A,314,1091,1488
B,196,10455,327
C,557,51635228,13793
D,55,14655464,1681
E,318,547,4899
F,166,145,170
G,17,890,169
H,54,946759,17229
R语言读入数据文件
weibo<-read.csv(file="weibo.csv",header=FALSE)
names(weibo)<-c("id","follow","fans","tweet")
1). 方法一,简单相加法
> data.frame(weibo[1],rank=rowSums(weibo[2:4]))
id rank
1 A 2893
2 B 10978
3 C 51649578
4 D 14657200
5 E 5764
6 F 481
7 G 1076
8 H 964042
这种方法简单粗暴的方式,是否能代码公平的打分呢?!
2). 方法二,加权求和
通过a,b,c的3个参数,分别设置权重求和。与方法一存在同样的问题,a,b,c的权值都是人为指定的,也是不能表示公平的打分的。
除了上面的两个方法,你能否想到不一样的思路呢!
3. 算法模型:PeopleRank算法
基于PageRank的理论,我们以每个微博账户的“关注”为链出链接,“粉丝”为链入链接,我们把这种以人为核心的关系,叫PeopleRank。
关于PageRank的介绍,请参考文章:PageRank算法R语言实现
PeopleRank假设条件:
- 数量假设:如果一个用户节点接收到的其他用户“关注”的数量越多,那么这个用户越重要。
- 质量假设:用户A的“粉丝”质量不同,质量高的“粉丝”会通“关注”接向其他用户传递更多的权重。所以越是质量高的“用户”关注用户A,则用户A越重要。
衡量PeopleRank的3个指标:
- 粉丝数
- 粉丝是否有较高PeopleRank值
- 粉丝关注了多少人
我们以下的数据为例,构造基于微博的数据模型:
(由于微博数据已增加访问权限,我无法拿到当前的实际数据,我用以前@晒粉丝应用,收集到的微博数据为例,这里ID已经过处理)
测试数据集:people.csv
- 25个用户
- 66个关系,关注和粉丝的关系
数据集: people.csv
1,19
1,21
2,11
2,17
2,21
3,1
3,20
3,2
3,7
3,6
3,10
4,3
4,6
5,19
5,11
5,2
6,4
6,12
6,18
6,15
6,10
6,5
7,9
7,18
7,10
8,3
8,11
8,7
8,16
8,14
9,6
10,8
10,18
11,13
11,3
12,9
12,4
12,16
12,5
13,19
13,1
13,6
14,7
14,17
14,19
14,1
14,5
14,2
15,11
15,14
15,12
16,20
17,4
17,6
18,10
18,11
18,15
18,14
19,18
20,10
20,5
21,24
22,11
23,17
24,15
25,24
第一列为用户ID,第二列也是用户ID。第一列用户,关注了第二用户。
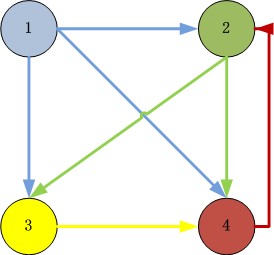
以R语言可视化输出
R语言程序
library(igraph)
people<-read.csv(file="people.csv",header=FALSE)
drawGraph<-function(data){
names(data)<-c("from","to")
g <- graph.data.frame(data, directed=TRUE)
V(g)$label <- V(g)$name
V(g)$size <- 15
E(g)$color <- grey(0.5)
g2 <- simplify(g)
plot(g2,layout=layout.circle)
}
drawGraph(people)
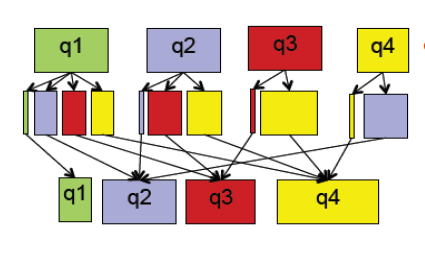
用R语言构建PeopleRank的算法原型
- 构建邻接矩阵
- 变换概率矩阵
- 递归计算矩阵特征值
- 标准化结果
- 对结果排序输出
R语言算法模型
#构建邻接矩阵
adjacencyMatrix<-function(pages){
n<-max(apply(pages,2,max))
A <- matrix(0,n,n)
for(i in 1:nrow(pages)) A[pages[i,]$dist,pages[i,]$src]<-1
A
}
#变换概率矩阵
dProbabilityMatrix<-function(G,d=0.85){
cs <- colSums(G)
cs[cs==0] <- 1
n <- nrow(G)
delta <- (1-d)/n
A <- matrix(delta,n,n)
for (i in 1:n) A[i,] <- A[i,] + d*G[i,]/cs
A
}
#递归计算矩阵特征值
eigenMatrix<-function(G,iter=100){
n<-nrow(G)
x <- rep(1,n)
for (i in 1:iter) x <- G %*% x
x/sum(x)
}
#直接计算矩阵特征值
calcEigenMatrix<-function(G){
x <- Re(eigen(G)$vectors[,1])
x/sum(x)
}
PeopleRank计算,带入数据集people.csv
people<-read.csv(file="people.csv",header=FALSE)
names(people)<-c("src","dist");people
A<-adjacencyMatrix(people);A
G<-dProbabilityMatrix(A);G
q<-calcEigenMatrix(G);
q
[1] 0.03274732 0.03404052 0.05983465 0.03527074 0.04366519 0.07042752 0.02741232
[8] 0.03378595 0.02118713 0.06537870 0.07788465 0.03491910 0.03910097 0.05076803
[15] 0.06685364 0.01916392 0.02793695 0.09450614 0.05056016 0.03076591 0.02956243
[22] 0.00600000 0.00600000 0.03622806 0.00600000
我们给这25用户进行打分,从高到低进行排序。
对结果排序输出:
result<-data.frame(userid=userid,PR=q[userid])
result
userid PR
1 18 0.09450614
2 11 0.07788465
3 6 0.07042752
4 15 0.06685364
5 10 0.06537870
6 3 0.05983465
7 14 0.05076803
8 19 0.05056016
9 5 0.04366519
10 13 0.03910097
11 24 0.03622806
12 4 0.03527074
13 12 0.03491910
14 2 0.03404052
15 8 0.03378595
16 1 0.03274732
17 20 0.03076591
18 21 0.02956243
19 17 0.02793695
20 7 0.02741232
21 9 0.02118713
22 16 0.01916392
23 22 0.00600000
24 23 0.00600000
25 25 0.00600000
查看评分最高的用户18的关系数据:
people[c(which(people$src==18), which(people$dist==18)),]
src dist
55 18 10
56 18 11
57 18 15
58 18 14
19 6 18
24 7 18
33 10 18
59 19 18
粉丝的PeopleRank排名:
which(result$userid %in% people$src[which(people$dist==18)])
[1] 3 5 8 20
粉丝的关注数:
table(people$src)[people$src[which(people$dist==18)]]
6 7 10 19
6 3 2 1
数据解释:用户18
- 有4个粉丝为别是6,7,10,19。(粉丝数)
- 4个粉丝的PeopleRank排名,是3,5,8,20。(粉丝是否有较高PeopleRank值)
- 粉丝的关注数量,是6,3,2,1。(粉丝关注了多少人)
因此,通过对上面3个指标的综合打分,用户18是评分最高的用户。
通过R语言实现的计算模型,已经比较符合我们的评分标准了,下面我们把PeopleRank用MapReduce实现,以满足对海量数据的计算需求。
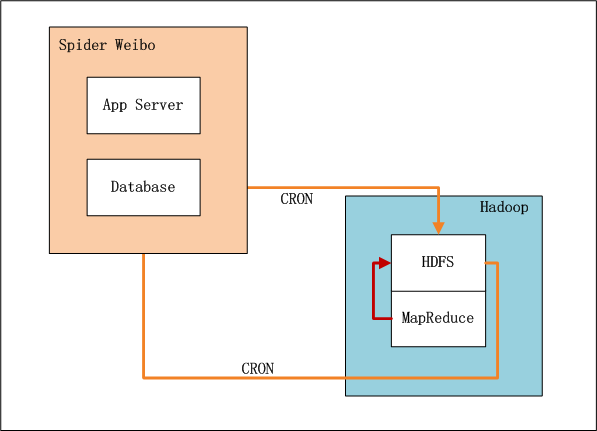
4. 架构设计:PeopleRank计算引擎系统架构
上图中,左边是数据爬虫系统,右边是Hadoop的HDFS, MapReduce。
- 数据爬虫系统实时爬取微博数据
- 设置系统定时器CRON,每xx小时,增量向HDFS导入数据(userid1,userid2)
- 完成导入后,设置系统定时器,启动MapReduce程序,运行推荐算法。
- 完成计算后,设置系统定时器,从HDFS导出推荐结果数据到数据库,方便以后的及时查询。
5. 程序开发:PeopleRank算法实现
win7的开发环境 和 Hadoop的运行环境 ,请参考文章:用Maven构建Hadoop项目
开发步骤:
- 微博好友的关系数据: people.csv
- 出始的PR数据:peoplerank.csv
- 邻接矩阵: AdjacencyMatrix.java
- PeopleRank计算: PageRank.java
- PR标准化: Normal.java
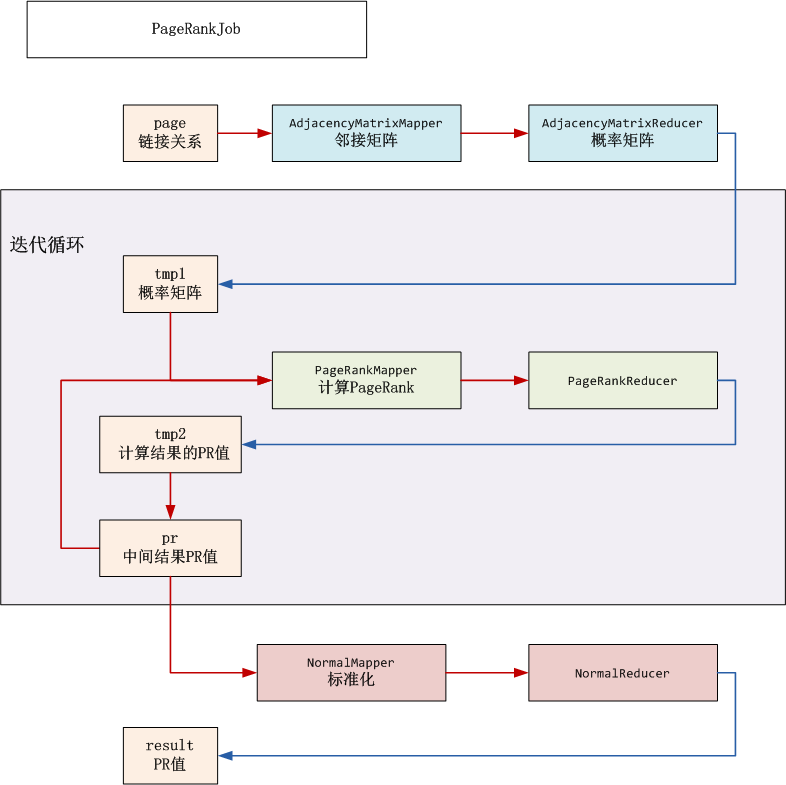
- 启动程序: PageRankJob.java
1). 微博好友的关系数据: people.csv,在上文中已列出
2). 出始的PR数据:peoplerank.csv
1,1
2,1
3,1
4,1
5,1
6,1
7,1
8,1
9,1
10,1
11,1
12,1
13,1
14,1
15,1
16,1
17,1
18,1
19,1
20,1
21,1
22,1
23,1
24,1
25,1
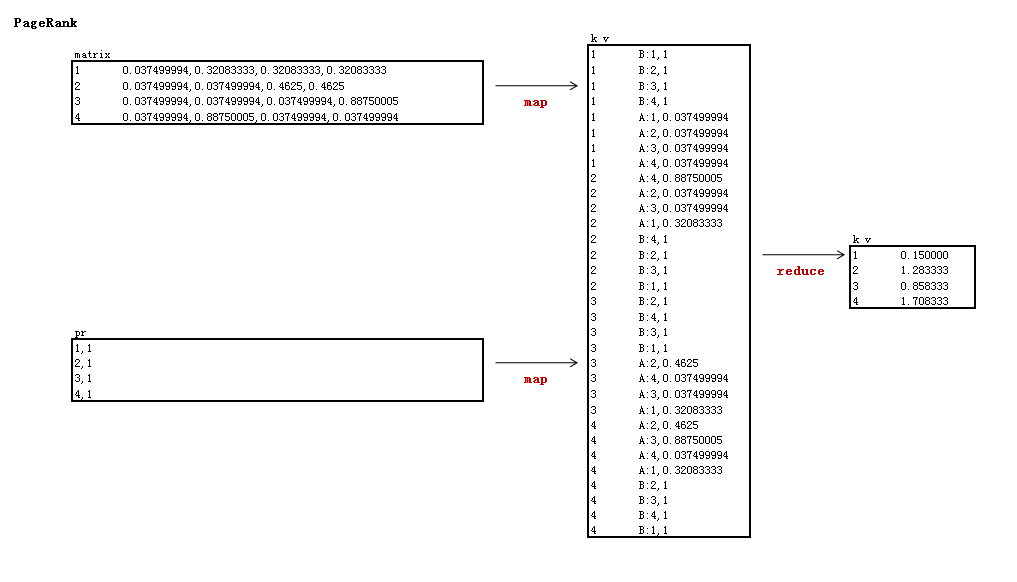
3). 邻接矩阵
矩阵解释:
- 阻尼系数为0.85
- 用户数为25
- reduce以行输出矩阵的列,输出列主要用于分步式存储,下一步需要转成行
部分数据输出:
~ hadoop fs -cat /user/hdfs/pagerank/tmp1/part-r-00000|head -n 4
1 0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.43100002,0.005999999,0.43100002,0.005999999,0.005999999,0.005999999,0.005999999
10 0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.43100002,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.43100002,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999
11 0.005999999,0.005999999,0.43100002,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.43100002,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999
12 0.005999999,0.005999999,0.005999999,0.2185,0.2185,0.005999999,0.005999999,0.005999999,0.2185,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.2185,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999,0.005999999
4). PeopleRank计算: PageRank.java
迭代一次的PeopleRank值
~ hadoop fs -cat /user/hdfs/pagerank/pr/part-r-00000
1 0.716666
10 1.354167
11 2.232500
12 0.575000
13 0.575000
14 0.815833
15 1.354167
16 0.532500
17 1.425000
18 1.850000
19 1.283334
2 0.716667
20 1.141667
21 0.858333
22 0.150000
23 0.150000
24 1.850000
25 0.150000
3 1.170001
4 0.929167
5 1.070833
6 2.275001
7 0.603333
8 0.575000
9 0.645833
5). PR标准化: Normal.java
迭代10次,并标准化的结果:
~ hadoop fs -cat /user/hdfs/pagerank/result/part-r-00000
1 0.032842
10 0.065405
11 0.077670
12 0.034864
13 0.039175
14 0.050574
15 0.066614
16 0.019167
17 0.027990
18 0.094460
19 0.050673
2 0.034054
20 0.030835
21 0.029657
22 0.006000
23 0.006000
24 0.036111
25 0.006000
3 0.059864
4 0.035314
5 0.043805
6 0.070516
7 0.027444
8 0.033715
9 0.021251
我们对结果进行排序
id pr
10 18 0.094460
3 11 0.077670
22 6 0.070516
7 15 0.066614
2 10 0.065405
19 3 0.059864
11 19 0.050673
6 14 0.050574
21 5 0.043805
5 13 0.039175
17 24 0.036111
20 4 0.035314
4 12 0.034864
12 2 0.034054
24 8 0.033715
1 1 0.032842
13 20 0.030835
14 21 0.029657
9 17 0.027990
23 7 0.027444
25 9 0.021251
8 16 0.019167
15 22 0.006000
16 23 0.006000
18 25 0.006000
第一名是用户18,第二名是用户11,第三名是用户6,第三名与之前R语言单机计算的结果有些不一样,而且PR值也稍有不同,这是因为我们迭代10次时,特征值还没有完全的收敛,需要更多次的迭代计算,才能得矩阵的特征值。
程序API的实现,请参考文章:PageRank算法并行实现
我们通过PageRank的模型,成功地应用到了社交网络,实现了PeopleRank的计算,通过设计数据挖掘算法,来取代不成熟的人脑思想。算法模型将更客观,更精准。
最后,大家可以利用这个案例的设计思路,认真地了解社交网络,做出属于的自己的算法。
由于时间仓促,代码可能存在bug。请有能力同学,自行发现问题,解决问题!!
######################################################
看文字不过瘾,作者视频讲解,请访问网站:http://onbook.me/video
######################################################
转载请注明出处:
http://blog.fens.me/hadoop-social-peoplerank/