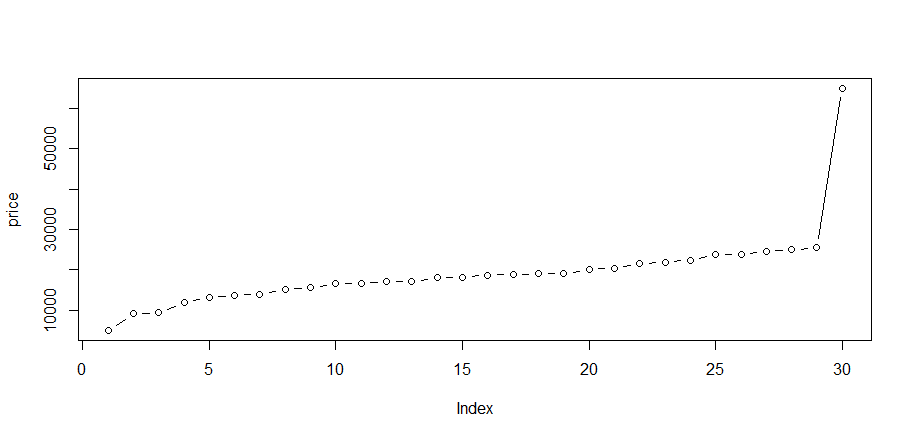算法为王系列文章,涵盖了计算机算法,数据挖掘(机器学习)算法,统计算法,金融算法等的多种跨学科算法组合。在大数据时代的背景下,算法已经成为了金字塔顶的明星。一个好的算法可以创造一个伟大帝国,就像Google。
算法为王的时代正式到来….
关于作者:
- 张丹, 分析师/程序员/Quant: R,Java,Nodejs
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-sampling-estimation
前言
在国家大选前夕,媒体进行民意调查,通过对不同地区不同职业的400人进行调查,其中的160人支持A,根据调查结果,媒体给出结论,A的民众支持度为40%。这个结论是否合理呢?
本文将继续上一篇文章抽样三步曲之一:R语言进行随机抽样sampling,将介绍如何使用抽样结果,进行抽样估计,推断出科学的结论。抽样三步曲系列文章:用R语言进行随机抽样,用R语言进行抽样估计和用R语言进行抽样校准。
目录
- 抽样估计介绍
- 点估计
- 抽样误差
- 区间估计
1. 抽样估计介绍
抽样估计(Sampling estimation)又称为抽样推断,是在抽样调查的基础上所进行的数据推测,即用样本数量特征来估计和推算总体数量特征。抽样估计,是对总体进行描述的另一种重要方法,具有花费小、适用性强、科学性高等特点。抽样估计,只能得到对总体特征近似的测试,因此抽样估计还必须同时考察所得结果的可能范围和可靠程度。
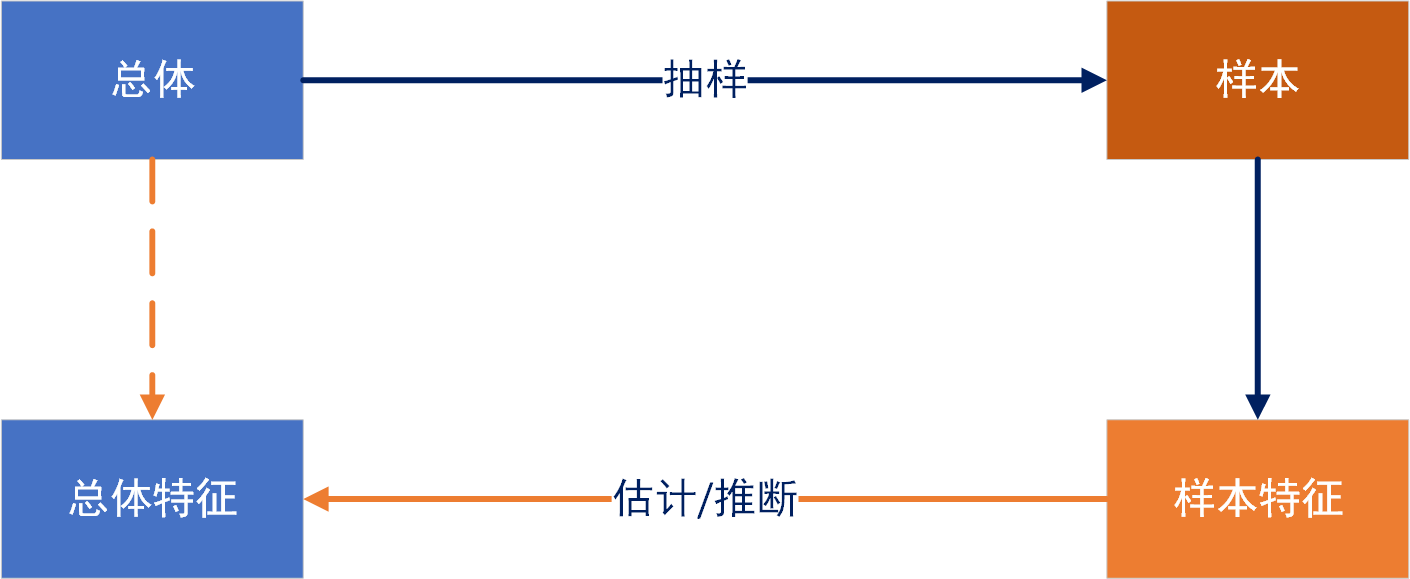
在现实场景中,我们对总体数据进行抽样得到的样本,分析样本的统计特征形成样本特征,然后利用样本特征对总体特征做一个估计或者推理。比如,采用样本均值对总体均值进行估计,采用样本方差对总体的方差进行估计,采用样本中某个特征的元素对总体中具有这个特征的元素进行估计等。
在统计学中,通常把总体特征也称为总体参数,总体参数是总体的某种特征值,是所研究的总体某些方面的数量表现。总体特征比如有总体均值,总体总值,总体比例,总体比率,总体方差等。统计估计,就是用对应的样本特征来估计出总体的特征。
抽样估计,使用大数定律做为用样本估计总体的基础理论,当样本量增大时,随机影响会相互抵消,样本均值与总体均值接近。使用中心极限定理进行区间估计的基础理论,只要方差有限,在样本足够多时,估计量的分布将趋于正态分布。
抽样估计,主要有两种方法点估计和区间估计。点估计,是通过样本估计量的某一次估计值来推断总体参数的可能取值。区间估计,是根据样本估计量以一定的可靠程序推断总体参数在所在区间的范围。
2. 点估计
点估计,又称定值估计,就是用实际样本指标数值作为总体参数的估计值。点估计的方法简单,一般不考虑抽样误差和可靠程度,它适用于对推断准确程度与可靠程度要求不高的情况。
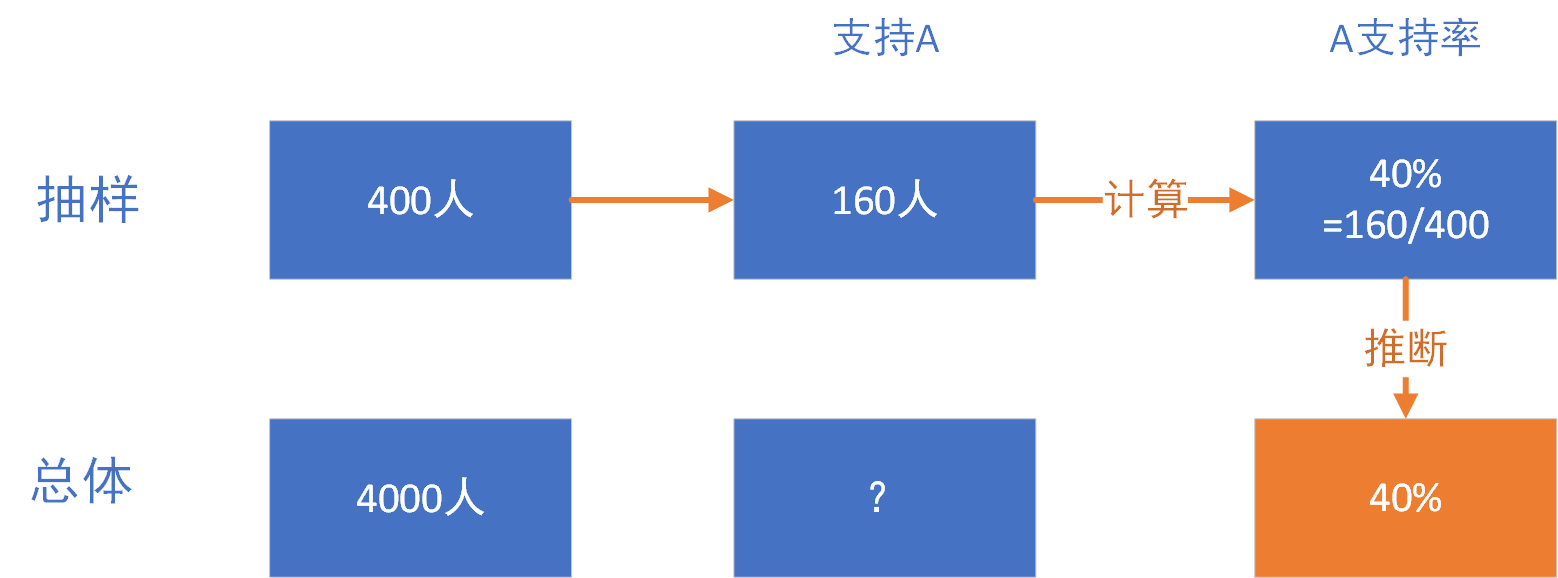
比如:支持率调查,从总体选民4000人中抽样400个人调查,其中有160人投票支持A,以此推断A在总体选民的支持率为40%(160/400)。这就是一个典型的点估计,用某个实际的抽样结果来推断总体的结果,但准确度可能不高。
投票支持率就是一个点估计的统计量,一个好的点估计统计量,必须满足具有3个性质:无偏性,一致性,有效性。
- 无偏性。即要求所有可能样本指标的平均数(样本指标的数学期望)与被估计的总体参数之间没有偏差。虽然每一次的样本指标值和总体指标值之间都可能有误差,但在多次反复的估计中,所有抽样指标值的平均数应该等于所估计的总体指标值本身,即用样本指标去估计总体参数,平均说来是没有偏误的。
- 一致性。用统计量估计总体参数要求当样本的单位数充分大时,抽样指标也充分地靠近总体指标。就是说,随着样本单位数n的无限增加,统计量和未知的总体参数之差的绝对值小于任意小的数,它的概率也趋近于1,即实际上是几乎肯定的。
- 有效性。以统计量估计总体参数时,优良估计量的方差应该比其他估计量的方差小。例如用样本平均数或总体某一变量值来估计总体平均数,虽然两者都是无偏的,而且在每一次估计中,两种估计量和总体平均数都可能有离差,但样本平均数更靠近于总体平均数的周围,平均说来其离差比较小。所以对比说来,抽样平均数是更为有效的估计量。
显然上例中的,基于抽样选民投票率推断出40%支持率的结论,是不够科学合理的。我们需要设计更多的统计量,来对总体特征进行估计。
接下来,我们设计一个场景,来完成抽样估计的实验过程。假设总体选民4000人,分布在全国的20个地区,随机抽样400人(无重复)进行调查。计算抽样特征:样本平均工资年薪,样本工资方差,样本投票支持率。1次抽样的结果,可能不能说明问题,我们进行500次抽样,把每次抽样结果汇总,可以形成抽样特征的抽样分布。以样本特征的平均值,来估计总体特征,得出结论。
操作步骤如下:
- 生成总体数据
- 抽样获得样本,并计算样本特征
- 多次抽样
- 抽样分布
- 获得结论
1. 生成总体数据
生成总体选民4000人数据。
# N总体4000人
> N<-4000
# 工资,使用均匀分布和正态分布进行叠加
> set.seed(0)
> salary1<-runif(2000,30000,80000) # 均匀分布
> set.seed(0)
> salary2<-rnorm(2000,51814,3000) # 正态分布
> salary<-c(salary1,salary2)
# 20个地区
> set.seed(1) #设置随机种子
> area<-sample(1:20,N,TRUE)
# 投票,1为投票给A,0为不投票给A
> set.seed(2) #设置随机种子
> vote<-sample(1:N,1500)
# 总体数据集
> df<-data.frame(salary,area)
> df$area<-as.factor(df$area)
> df$vote<-0
> df$vote[vote]<-1
> df$vote<-as.factor(df$vote)
# 查看数据前10条
> head(df,10)
salary area vote
1 74834.86 4 0
2 43275.43 7 0
3 48606.19 1 1
4 58642.67 2 0
5 75410.39 11 0
6 40084.10 14 0
7 74919.48 18 0
8 77233.76 19 1
9 63039.89 1 0
10 61455.70 10 1
# 查看统计概率
> summary(df)
salary area vote
Min. :30030 13 : 226 0:2500
1st Qu.:48302 20 : 217 1:1500
Median :52015 9 : 215
Mean :53254 14 : 215
3rd Qu.:56654 8 : 211
Max. :79997 6 : 206
(Other):2710
总体数据集,包括3列:
- salary,每个选民的工资
- area,每个选民所在地区,1到20
- vote,对A的投票
2. 抽样获得样本,并计算样本特征
进行随机抽样,选出400人。
# 加载工具包
> library(sampling)
> library(plyr)
> library(magrittr)
# 抽样400人
> s<-400
> set.seed(30) # 随机种子
> s1<-srswor(s,N) # 简单随机抽样
# 样本数据集
> sample_df<-getdata(df,s1)
# 样本工资均值
> mean(sample_df$salary)
[1] 53936.74
# 样本工资标准差
> sd(sample_df$salary)
[1] 10930.51
# 样本工资方差
> var(sample_df$salary)
[1] 119476082
# 样本投票比例
> table(sample_df$vote)
0 1
242 158
# 地区分布
> table(sample_df$area)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
12 21 24 17 22 17 20 25 19 17 20 15 24 24 18 22 20 23 26 14
对选样本选民资进行正态分布检验。
> shapiro.test(sample_df$salary)
Shapiro-Wilk normality test
data: sample_df$salary
W = 0.94848, p-value = 1.389e-10
# 画出qq图
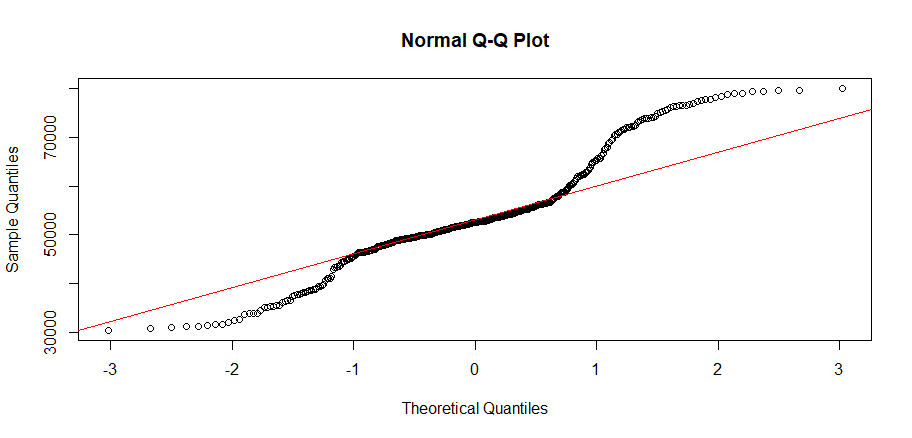
> qqnorm(sample_df$salary)
> qqline(sample_df$salary,col="red")
由于p-value=0.1389 > 0.05,不能拒绝正在分布的假设,所以,工资符合正态分布。但从图中看,已经偏离很大了。这样我们就完成一次抽样的过程了。
3. 多次抽样
1次抽样不能说明什么问题,我们进行多次抽样,进行500次随机抽样,可能得到不同的结果,形成不同的抽样分布。
# 定义抽样数据框
> sample500<-data.frame(time=1:500,mean=0,var=0,vote=0)
# 进行500次随机抽样
> for(i in 1:500){
+ s1<-srswor(s,N)
+ sample_df<-getdata(df,s1)
+ sample500$mean[i]<-mean(sample_df$salary)
+ sample500$var[i]<-var(sample_df$salary)
+ sample500$vote[i]<-length(which(sample_df$vote==1))/s
+ }
# 查看前6条数据
> head(sample500)
time mean var vote
1 1 53457.14 118965345 0.4000
2 2 53138.77 98917316 0.4150
3 3 52852.20 113358728 0.3925
4 4 53655.00 104086558 0.3525
5 5 52530.54 107175129 0.3625
6 6 53491.33 119491300 0.3700
这时,我们完成了500次的抽样,并把抽样的结果进行了整理。
4. 抽样分布
为了观察方例,以柱状图进行可视化,查看每个统计量的抽样分布。
# 图片输出布局,一行三列
> par(mfrow=c(1,3))
# 输出样本均值,样本方差,样本投票率的柱状图
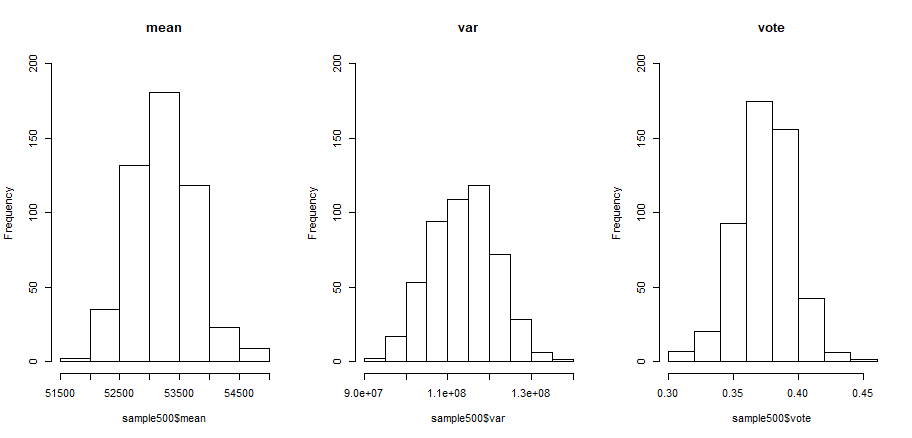
hist(sample500$mean,10,ylim=c(0,200),main='mean')
hist(sample500$var,10,ylim=c(0,200),main='var')
hist(sample500$vote,10,ylim=c(0,200),main='vote')
从图中可以观察到样本均值、样本方差和投票支持率,都看起来都呈现正态分布的形状。根据抽样分布性质,当总体分布已知且为正态分布或接近正态分布时,无论样本容量大小,样本均值都为正态分布。当总体分布未知,根据中心极限定理,样本容量足够大时趋近于正态分布。经验上验证,当样本容量大于30时,样本均值接近正态分布。
接下来,我们分别进行正态分布的检查。
# 均值的正态分布检查
> shapiro.test(sample500$mean)
Shapiro-Wilk normality test
data: sample500$mean
W = 0.99745, p-value = 0.6438
# 方差的正态分布检查
> shapiro.test(sample500$var)
Shapiro-Wilk normality test
data: sample500$var
W = 0.99503, p-value = 0.1084
# 投票率的正态分布检查
> shapiro.test(sample500$vote)
Shapiro-Wilk normality test
data: sample500$vote
W = 0.99465, p-value = 0.07877
左一图,500次抽样的工资的均值,为正态分布,而且p-value远大于0.05,比之前1次的抽样效果好很多。
5. 获得结论
我们检验的结果与性质相符合,由于样本特征都满足正态分布,所以我们以这3个样本特征的均值,做为总体特征的点估计值,说服力就会更强一些。
> colMeans(sample500[,c("mean","var","vote")])
mean var vote
5.323558e+04 1.136433e+08 3.751550e-01
计算500次抽样的样本特征的均值,民选平均年薪为53235.58元,对A的投票支持率为37.52%。
3. 抽样误差
在抽样调查中,通常调查结果和实际结果之间会有一定的偏差,根据形成原因不同,一般会分抽样误差和非抽样误差。
非抽样误差可以产生于抽样调查的各个阶段,包括抽样调查及抽样设计、数据采集及数据的处理与分析阶段。非抽样误差的产生不是由于抽样的随机性,而是由于其他多种原因引起的,主观因素偏多。
抽样误差,表示总体的点估计与总参数之间的差异,是由样本统计量推断总体参数时的误差,是不可避免的。抽样误差,会随着样本量增大而减小,受总体变异大小影响,抽样方法不同也会产生误差。
在上面的场景中,用总体数据的实际值与点估计值进行对比。
| 数据集 | 数量 | salary均值 | vote投票支持率 |
| 总体 | 4000 | 53253.55 | 37.5% |
| 1次抽样 | 400 | 54170.98 | 39.5% |
| 500次抽样 | 400*500 | 53235.58 | 37.52% |
我们观察到,1次抽样得到的点估计值与总体参数之间是存在较大的误差,这个误差被称为抽样误差。而进行500次的抽样后的估计值与总体参数之间,误差明显缩小了许多。
抽样分布的目的,就是为了确保我们在使用点估计值进行总体估计的时候能够清楚的知道误差的范围到底有多大,该如何去调整抽样的大小或采取相应的校正以使得其可以更加准确的近似总体的参数。
对抽样效果的评估时,当样本容量相同,抽样的样本误差越小,则效果越好。我们可以使用样本均值的标准差统计量,描述样本的误差,对抽样效果进行评价。样本均值的标准差可用来度量均值与总体均值的距离,即为可能的误差,又被称为均值标准误。
N为总体数量,s为样本数量
均值标准误,有限总体:
sd_sample = sqrt((N-s)/(N-1)) * (sd_total / sqrt(s))
其中,fpc = sqrt((N-s)/(N-1))为有限总体修正因子
均值标准误,无限总体:
sd_sample = sd_total / sqrt(s)
如果总体很大样本很小,当s/N<=0.05时,样本不足5%时,有限总体修正因子趋近于1.
计算场景中均值标准误。
> N<- 4000
> s<- 400
# 在有限个总体的情况下,修正因子
> fpc<-sqrt((N-s)/(N-1)) ;fpc
[1] 0.9488019
# 均值标准误
> fpc * sd(df$salary) / sqrt(sd(sample500$mean))
[1] 447.9483
抽样误差,为样本统计量的估计值与要测度的总体参数值之间的绝对差距。抽样分布能够用来提供抽样误差大小的可能(概率)。
# 总体均值为红色线
> total_mean<-mean(df$salary)
> par(mfrow=c(1,4))
> hist(sample500$mean[1:30],breaks=20,xlim=c(51000,55000),ylim=c(0,80),main="30")
> abline(v = total_mean,col="red")
> hist(sample500$mean[1:100],breaks=20,xlim=c(51000,55000),ylim=c(0,80),main="100")
> abline(v =total_mean,col="red")
> hist(sample500$mean[1:200],breaks=20,xlim=c(51000,55000),ylim=c(0,80),main="200")
> abline(v =total_mean,col="red")
> hist(sample500$mean[1:500],breaks=20,xlim=c(51000,55000),ylim=c(0,80),main="500")
> abline(v =total_mean,col="red")
在上面场景中,抽样的次数越多,样本的均值越集中于实际的均值。如果媒体认为被抽样的选中的选民,他们的工资与总体的工资均值(53253.55)误差在200元内是合理的抽样,那么我们可以把问题转化为,计算标准正态分布工资在200元以内的可能性是多少,即抽样落在[53253.55-200, 53253.55+200]区间的概率。
# 标准正态分布概率
> ((53253.55+200)-(53253.55-200))/447.9483
[1] 0.8929602
# 计算面积
> pnorm(0.8929602, 0, 1)
[1] 0.8140608
在上述的简单随机抽样中,有81.41%的概率,使得样本均值与总体实际均值误差不超过200元。所以,上面的场景中,媒体有81.41%的概率会抽中他们目标的选民,1次抽样会造成偏差,当经过500次的抽样后,取投票率的平均值是科学合理的。
4. 区间估计
由于点估计始终会存在一定的估计误差,对于未知参数点估计值只是一个近似值。那么我们在进行估计时,不要给出一个具体值,而是给出一个区间值,可能是更合适,也是更可信的,就能解决估计不准的问题。
举个例子,去欧洲旅游10日自由行,你做预算时,可能给不出准确的花费18000元还20000元,你通常会说一个大概的范围,比如15000元到30000元之间,也可能是18000元到18500元之间。如果给出的范围太大,虽然可信度高,但没有什么参考意义;如果给出的范围大小,准确度高了,但是可信度又变低了。找到一个合适的估计范围,可以置信区间来解决。
区间估计,是根据样本指标、抽样误差和概率保证程度去推断总体参数的可能范围。在统计学中,通常用置信区间及样本出现的概率来估计总体参数,以一定的概率保证总体参数包含在估计区间内。区间估计要完成两个方面的估计:1是根据样本指标和抽样平均误差估计总体指标的可能范围,2是估计推断总体指标真实值在这个范围的可靠程度。
置信区间涉及两个问题,一个是置信水平,另一个是如何建立置信区间。所谓置信水平就是给出一个区间的信心,这个信心以概率来表示,绝大多数情况下取0.95,表示你对所估计的总体参数有95%的信心落在你所给的区间内。通常置信水平以1-alpha表示,alphe称为显著性水平。
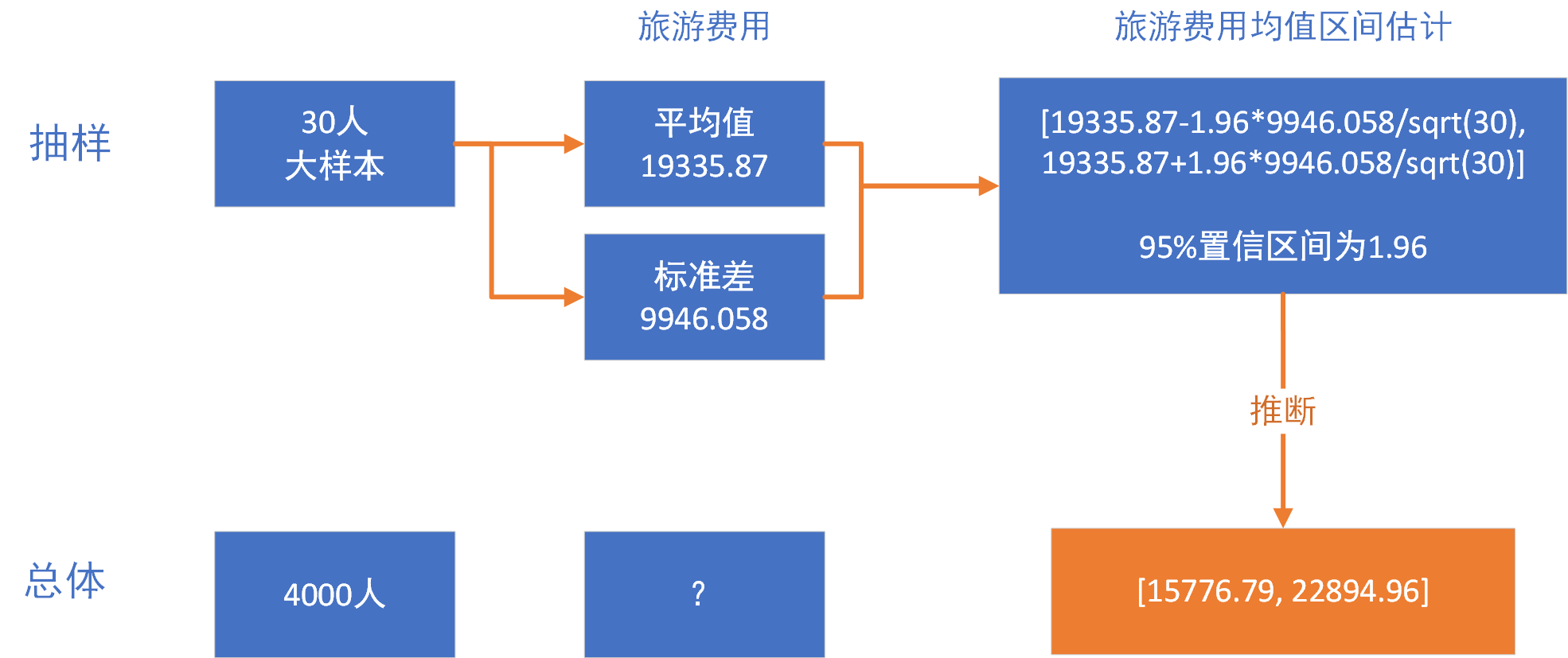
继续上面欧洲旅游例子:我们从网上找到去过自游行去过欧洲旅游的人,找到了30个人为样本,样本的平均花费是为19377元,最低的5000元,最高的65000元,标准差为14750。我们以这个样本的95%的置信区间为标准计算,推算本次旅游的预算。
首先,假设总体的均值为20000元,方差为5000,生成样本数据集30个样本。
> total_m<-20000 # 总体均值
> total_sd<-5000 # 总体标准差
> s<-30 # 样本数据
> min<-5000 # 样本最小值
> max<-65000 # 样本最大值
# 生成样本数据
> set.seed(10)
> price<-rnorm(s-2,total_m,total_sd) # 正态分布
# 查看样本数据
> price<-c(min,max,price);price # 拼接最大值,最小值
[1] 5000.000 65000.000 20093.731 19078.737 13143.347
[6] 17004.161 21472.726 21948.972 13959.619 18181.620
[11] 11866.637 18717.608 25508.898 23778.908 18808.832
[16] 24937.224 23706.951 20446.736 15225.281 19024.248
[21] 24627.606 22414.893 17018.447 9073.566 16625.670
[26] 9404.694 13674.010 18131.692 16562.223 15639.206
# 样本均值
> sample_m<-mean(price);sample_m
[1] 19335.87
# 样本标准差
> sample_sd<-sd(price);sample_sd
[1] 9946.058
画出样本数据,x轴为样本点序号,y轴为旅游的花费
# 排序
> price<-price[order(price)]
# 画出散点图
> plot(price,type='both')
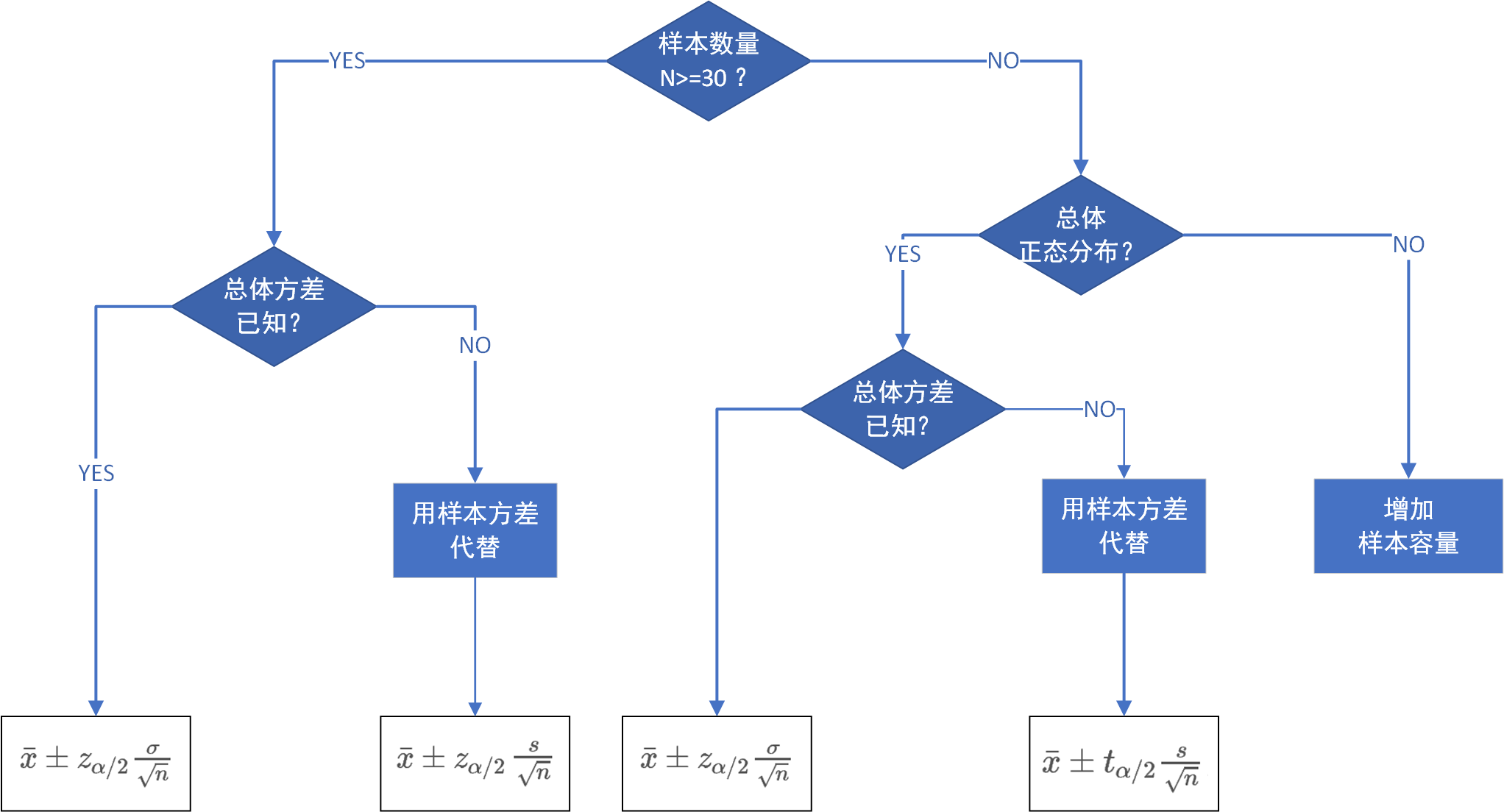
接下来,我们会分几种情况,进行区间估计。
- 大样本(>=30),已知总体方差,对总体均值进行区间估计。
- 大样本(>=30),未知总体方差,对总体均值进行区间估计。
- 小样本(<30),总体符合正态分布时,已知总体方差。
- 小样本(<30),总体符合正态分布时,未知总体方差。
公式解释:
- 样本均值: x¯
- 样本数量: n
- 样本方差: s
- 总体方差: σ
- Z分布:z
- T分布: t
- 显著性水平alpha: α
从总体均值的估计程序中,其实就可以为2种情况,是否已知总体方差,已知总体方差就用总体方差,未知总体方差就样本方差。对于是否是正态分布的假设,可以根据中心极限定理的进行人为的预判。对于样本的数量,我们抽保证获得30个以上,在目前的大数据时代,应该没啥难度。
# 进行区间估计
# 参数为:样本,标准差,置信区间
> conf.int=function(x,sigma,conf.level=0.95) {
+ mean<-mean(x)
+ n<-length(x)
+ alpha<-1-conf.level
+ z=qnorm(1-alpha/2,mean=0,sd=1,lower.tail = T)
+ c(mean-sigma*z/sqrt(n),mean+sigma*z/sqrt(n))
+ }
当已知总体标准差时,对总体均值进行区间估计。
> conf.int(price,total_sd,0.95)
[1] 17546.68 21125.07
当未知总体标准差时,用样本方标准差代替,对总体均值进行区间估计。
> conf.int(price,sample_sd,0.95)
[1] 15776.79 22894.96
上面的过程,其实就是Z分布的检验过程,我们也可以直接使用Z分布的检验函数。
# 安装BSDA包
> install.packages('BSDA')
> library(BSDA)
# 当已知总体标准差时,对总体均值进行区间估计。
> z.test(price,sigma.x=total_sd)
One-sample z-Test
data: price
z = 21.181, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
17546.68 21125.07
sample estimates:
mean of x
19335.87
# 当未知总体标准差时,用样本方标准差代替,对总体均值进行区间估计。
> z.test(price,sigma.x=sd(price))
One-sample z-Test
data: price
z = 10.648, p-value < 2.2e-16
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
15776.79 22894.96
sample estimates:
mean of x
19335.87
我们用z分布检查,得到的计算结果,与手动计算的结果是一致的。
最后,如果我们实现无法获得大于30个样本,而总体分布未知,我们可以使用单总体的T检验进行区间估计。T检验的详细使用说明,请参考文章用R语言解读统计检验-T检验
> t.test(price)
One Sample t-test
data: price
t = 10.648, df = 29, p-value = 1.558e-11
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
15621.96 23049.79
sample estimates:
mean of x
19335.87
好的抽样方法,能让我们的样本有更好的代表性。那么好的抽样估计,可以让调查结论更科学、更合理,真正是起到事半功倍的效果。不要再随意拍脑袋做决定了,用统计的专业方法来改进工作吧。如果你想了解如何进行抽样,请参考上一篇文章抽样三步曲之一:R语言进行随机抽样sampling
转载请注明出处:
http://blog.fens.me/r-sampling-estimation