算法为王系列文章，涵盖了计算机算法，数据挖掘(机器学习)算法，统计算法，金融算法等的多种跨学科算法组合。在大数据时代的背景下，算法已经成为了金字塔顶的明星。一个好的算法可以创造一个伟大帝国，就像Google。

算法为王的时代正式到来….

关于作者：

• 张丹, 分析师/程序员/Quant: R,Java,Nodejs
• blog: http://blog.fens.me
• email: bsspirit@gmail.com

转载请注明出处：
http://blog.fens.me/r-sampling

前言

抽样是统计上的基本问题，在实现中生活有非常多的应用场景。美国大选时，媒体进行民意调查，通过对不同地区不同职业的少量人进行询问，就推算出谁的支持率更多。我们进到机场时，会被要求防爆检查，由于人力资源有限，并不是所有人都被检查，而是有一定几率的抽检，来防范重大的安全风险。做机器学习模型的时候，需要训练集和测试集，样本的好坏直接会影响到模型的训练效果。

这些问题其实都可以用统计学的抽样方法来解释和解决。抽样三步曲系列文章：用R语言进行随机抽样，用R语言进行抽样估计和用R语言进行抽样校准。

目录

1. 抽样的基本概念
2. 简单随机抽样
3. 分层抽样
4. 整群抽样
5. 系统抽样
6. PPS抽样和Brewer抽样

1. 抽样的基本概念

抽样，是一种可以基于样本的统计信息来获取总体信息，而无需分别调查每个个体信息的方法，其基本要求是要保证所抽取的样本对总体具有充分的代表性。

我们把包含所研究的全部个体的集合看作总体，构成总体的每一个元素作为个体，从总体中抽取一部分的个体所组成的集合叫做样本，样本中的个体数目叫做样本数量。

1.1 为什么需要抽样？

抽样，是为了从样本中得出有关人群的结论，以便通过直接观察群体的一部分（样本）来确定该人群的特征。

• 比起观察群体中的每个个体，观察样本所需的时间更少，所以观察样本效率更高效。
• 比起分析整个群体行为，分析样本更简单更方便，所以分析样本难度更小。

抽样会大量的帮助我们节约工作时间，减少工作量，降低分析难度。

1.2 抽样步骤
我们开始进行抽样时，可以按照标准抽样步骤来进行，从而保证抽样过程的合理性。通常来说，会按照下面5个步骤进行抽样。

抽样步骤解释：

• 第1步：界定总体，在具体抽样前，首先对从总抽取样本的总体范围与界限作明确的界定。比如进行民意调查的抽样，需要考虑18岁以上且有资格的人群。
• 第2步：制定抽样框，收集总体中全部抽样名单，构成抽样样本的个体或人群的列表。
• 第3步：决定抽样方法，可以使用概率抽样或非概率抽样，概率抽样方法是从客观上设计抽样规则，每个投票人都具有同样的价值，非概率抽样方法更多是主观上的抽样。
• 第4步：设置样本数量，样本中要采集的个人或物品的数量，要足够对这一人群做出精准的推断。样本量越大，对这一人群的推断就越准确。
• 第5步：实际抽取样本，一旦确定了目标人群、抽样框架、抽样技术和样本数量，就可以开始收集数据，进行抽样了。
• 第6步：评估样本质量，对样本的质量、代表性、偏差等等进行初步的检验和衡量，其目的是防止由于样本的偏差过大而导致的失误

1.3 抽样方法
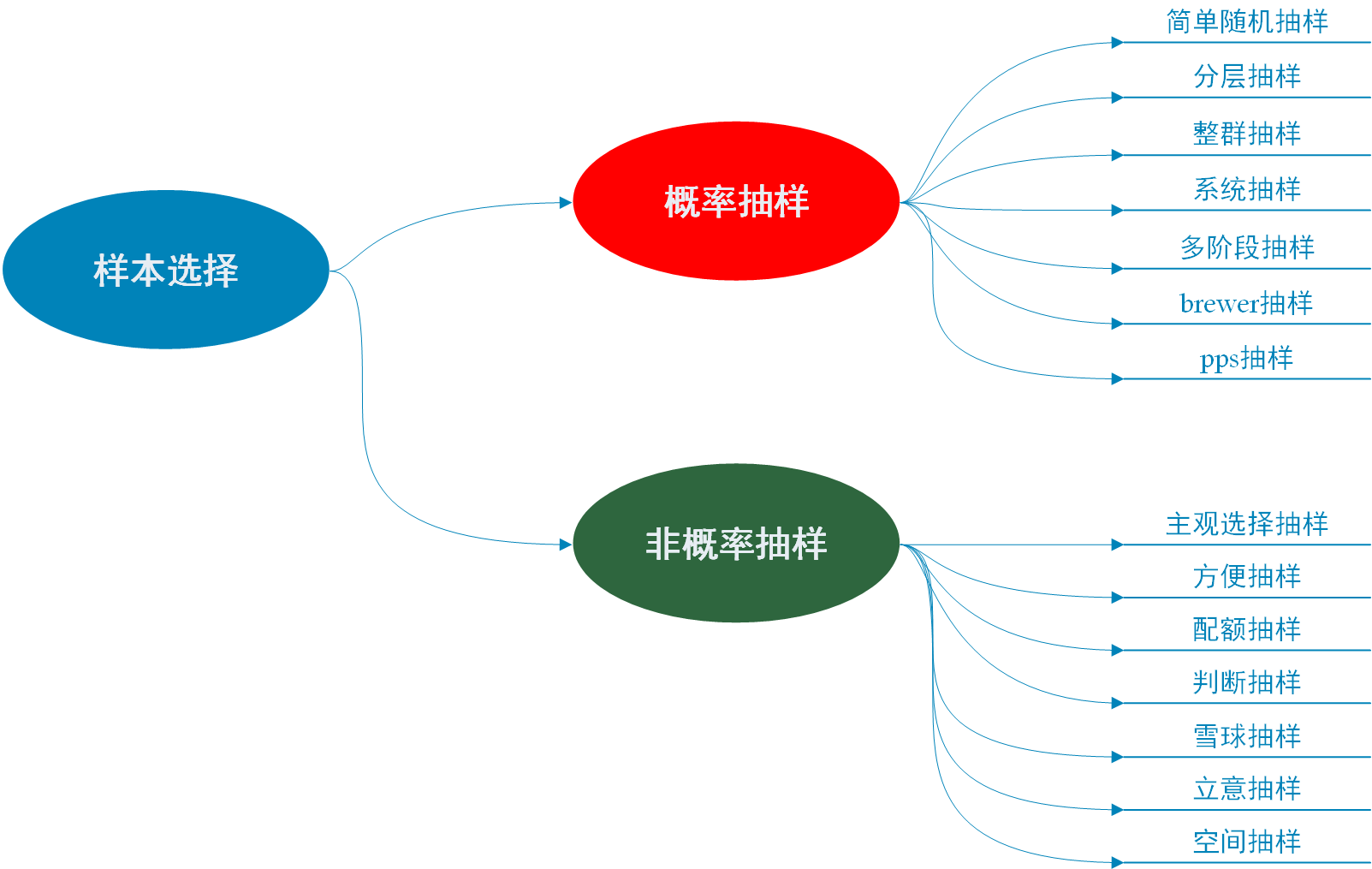
抽样方法，主要分为概率抽样和非概率抽样。

• 概率抽样：群体中的每个人都有被选择的平等机会，概率抽样提供了一个真正代表群体的样本，客观性强。
• 非概率抽样：群体中的每个人都没有被选择的平等机会。因此，可能出现非代表性样本，这种样本无法产生概括性的结果，主观性强。

本文的后面，将重点介绍概率抽样的各种方法。

1.4 有放回和无放回
我们在抽样的时候，需要考虑2种情况，一种是有放回的情况，另一种是无放回的情况。

• 有放回，指从总体集合中抽出一个元素后，再把这个元素放回总体集合，第二次可以继续抽到这个元素，样本不是唯一的。
• 无放回，指从总体集合中抽出一个元素后，不把这个元素放回总体集合，第二次可以不能抽到这个元素，样本都是唯一的。

我们假设总体数量为N，样本数量为s，从N个物体中抽取s个样本。

2. 简单随机抽样

简单随机抽样是指，从总体数据中任意抽取指定数量的数据作为样本，每个可能被抽取的样本概率相等。抽取方法分为：放回抽样，不放回抽样。

开发所使用的系统环境

• Win10 64bit
• R: 3.6.1 x86_64-w64-mingw32/x64 b4bit

在R语言中，我们可以用基础包的sample()函数进行随机抽样，使用自带的鸢尾花数据集iris。

使用sample()函数，总体数据为N=150个，抽取出样本s=15个。

# 打印数据集iris
> head(iris)
  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1          5.1         3.5          1.4         0.2  setosa
2          4.9         3.0          1.4         0.2  setosa
3          4.7         3.2          1.3         0.2  setosa
4          4.6         3.1          1.5         0.2  setosa
5          5.0         3.6          1.4         0.2  setosa
6          5.4         3.9          1.7         0.4  setosa

# 定义总体数和样本数
> N<-nrow(iris) # 总体
> s<-15         # 样本

> # 简单随机抽样，默认为无放回
> s1<-sample(N,s);s1
 [1]  27  33  16  86  43  36  79  98  10  44  82   4  19 145  75

# 打印抽样结果
> iris[s1,]
    Sepal.Length Sepal.Width Petal.Length Petal.Width    Species
27           5.0         3.4          1.6         0.4     setosa
33           5.2         4.1          1.5         0.1     setosa
16           5.7         4.4          1.5         0.4     setosa
86           6.0         3.4          4.5         1.6 versicolor
43           4.4         3.2          1.3         0.2     setosa
36           5.0         3.2          1.2         0.2     setosa
79           6.0         2.9          4.5         1.5 versicolor
98           6.2         2.9          4.3         1.3 versicolor
10           4.9         3.1          1.5         0.1     setosa
44           5.0         3.5          1.6         0.6     setosa
82           5.5         2.4          3.7         1.0 versicolor
4            4.6         3.1          1.5         0.2     setosa
19           5.7         3.8          1.7         0.3     setosa
145          6.7         3.3          5.7         2.5  virginica
75           6.4         2.9          4.3         1.3 versicolor

sample()函数，默认是不放回的抽样，保证每个结果是唯一的。我们在某些场景下，也会用到放回抽样，在使用sample()函数时，增加一个参数。通过放回抽样的方法，抽出来的结果就会有重复。

> s1a<-sample(N,s,TRUE);s1a # 有放回
 [1]  57  27  57 100  51  93  81 137  46  96   7  15 114  24  34

在R语言中专门有一个包用来进行随机抽样，sampling包。后面，我们的抽样方法，都会基于sampling包进行介绍。sampling包也提供了一个函数srswor()函数，可以进行简单随机抽样。

# sampling包安装
> install.packages("sampling")
> library(sampling)

# 使用srswor()函数，进行随机抽样，无放回抽样
> s2<-srswor(s,N)

# 打印被选中的索引
> s2
  [1] 1 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
 [49] 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 [97] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1
[145] 0 0 0 0 0 0

# 打印抽样结果
> getdata(iris,s2)
    ID_unit Sepal.Length Sepal.Width Petal.Length Petal.Width    Species
1         1          5.1         3.5          1.4         0.2     setosa
8         8          5.0         3.4          1.5         0.2     setosa
10       10          4.9         3.1          1.5         0.1     setosa
20       20          5.1         3.8          1.5         0.3     setosa
22       22          5.1         3.7          1.5         0.4     setosa
28       28          5.2         3.5          1.5         0.2     setosa
48       48          4.6         3.2          1.4         0.2     setosa
54       54          5.5         2.3          4.0         1.3 versicolor
78       78          6.7         3.0          5.0         1.7 versicolor
81       81          5.5         2.4          3.8         1.1 versicolor
82       82          5.5         2.4          3.7         1.0 versicolor
117     117          6.5         3.0          5.5         1.8  virginica
127     127          6.2         2.8          4.8         1.8  virginica
136     136          7.7         3.0          6.1         2.3  virginica
144     144          6.8         3.2          5.9         2.3  virginica

ID_unit列，是新增加的一列，把索引序号直接加在结果数据集了，方便我们肉眼识别随机数是否均匀。

有放回的抽样，可以使用srswr()函数，当有重复选择时，数据会出现大于1的情况，比如第46个值被抽出来2次。

# 有放回抽样
> s2a<-srswr(s,N);s2a 
  [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1
 [49] 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 0 0 0
 [97] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0
[145] 0 0 0 0 0 0

# 查看被抽样数据的数量
> table(s2a)
s2a
  0   1   2 
136  13   1 

简单随机抽样，是最简单，也是最常被大家所使用的。

3. 分层抽样

分层抽样是将抽样单位按某种特征或者某种规则划分为不同的层，然后从不同的层中规定的比例，独立、随机的抽取样本，最后将个层的样本结合起来，对总体的目标量估计。分层抽样的优点是样本的代表性比较好，抽样误差比较小。举例说明：对药品进行抽查合格率，从生产环境，运输环节，销售环境进行分层抽样，每个环节按一定的比例抽取药品进行检查。

下面我们使用strata()函数，来模拟分层抽样的操作。取iris鸢尾花的数据集，以Species种属作为分层标准，把数据分成3个层，按照1:3:2的比例进行抽样。

# 判断每个类型的数量
> table(iris$Species)
    setosa versicolor  virginica 
        50         50         50 

# 设置抽样比例为1:3:2
> size <-c(1,3,2)

# 进行分层抽样
> s4=strata(iris,c("Species"),size=size, method="srswor");s4
       Species ID_unit Prob Stratum
47      setosa      47 0.02       1
75  versicolor      75 0.06       2
83  versicolor      83 0.06       2
84  versicolor      84 0.06       2
112  virginica     112 0.04       3
132  virginica     132 0.04       3

# 查看抽样的数据集
> getdata(iris,s4)
    Sepal.Length Sepal.Width Petal.Length Petal.Width    Species ID_unit Prob Stratum
47           5.1         3.8          1.6         0.2     setosa      47 0.02       1
75           6.4         2.9          4.3         1.3 versicolor      75 0.06       2
83           5.8         2.7          3.9         1.2 versicolor      83 0.06       2
84           6.0         2.7          5.1         1.6 versicolor      84 0.06       2
112          6.4         2.7          5.3         1.9  virginica     112 0.04       3
132          7.9         3.8          6.4         2.0  virginica     132 0.04       3

结果的数据集增加了3列，ID_unit为索引序号，Prob为被抽样的概率，Stratum为分层的层号。这样就完成了分层抽样。

4. 整群抽样

整群抽样又称聚类抽样，是将总体中各单位归并成若干个互不交叉、互不重复的集合，然后以群为抽样单位抽取样本的一种抽样方式。

整群抽样与分层抽样是容易被混淆的，分层抽样是将抽样单位按某种特征或某种规则划分为不同的层，然后从不同的层中独立，随机地抽取样本。整群抽样则是将总体中若干个单位合并为群，抽样时直接抽取群，然后对选中群中的所有单位全部实施调查。

区别点：分层抽样要求各层之间的差异很大，层内个体或单元差异小，而整群抽样要求群与群之间的差异比较小，群内个体或单元差异大。分层抽样的样本是从每个层内抽取若干单元或个体构成，而整群抽样则是要么整群抽取，要么整群不被抽取。

下面我们使用cluster()函数，来模拟整群抽样的操作。取iris鸢尾花的数据集，以Sepal.Length萼片长度作为分群标准，把数据分成3个群进行抽样。

首先，查看Sepal.Length列数据的分布情况

# 加载工具包
> library(magrittr)
> library(plyr)

# 查看Sepal.Length列数据的分布情况
> Sepal_Length<-table(iris$Sepal.Length) %>% ldply
> names(Sepal_Length)<-c("Sepal.Length","times")
> Sepal_Length
   Sepal.Length times
1           4.3     1
2           4.4     3
3           4.5     1
4           4.6     4
5           4.7     2
6           4.8     5
7           4.9     6
8             5    10
9           5.1     9
10          5.2     4
11          5.3     1
12          5.4     6
13          5.5     7
14          5.6     6
15          5.7     8
16          5.8     7
17          5.9     3
18            6     6
19          6.1     6
20          6.2     4
21          6.3     9
22          6.4     7
23          6.5     5
24          6.6     2
25          6.7     8
26          6.8     3
27          6.9     4
28            7     1
29          7.1     1
30          7.2     3
31          7.3     1
32          7.4     1
33          7.6     1
34          7.7     4
35          7.9     1

以Sepal.Length列进行分群

> s5 <- cluster(iris,clustername="Sepal.Length",size=3,method="srswor",description=TRUE);s5
Number of selected clusters: 3 
Number of units in the population and number of selected units: 150 8 
  Sepal.Length ID_unit       Prob
1          4.5      42 0.08571429
2          6.8     113 0.08571429
3          6.8      77 0.08571429
4          6.8     144 0.08571429
5          6.9     121 0.08571429
6          6.9     140 0.08571429
7          6.9     142 0.08571429
8          6.9      53 0.08571429

# 打印抽样结果
> getdata(iris,s5)
    Sepal.Width Petal.Length Petal.Width    Species Sepal.Length ID_unit       Prob
42          2.3          1.3         0.3     setosa          4.5      42 0.08571429
113         3.0          5.5         2.1  virginica          6.8     113 0.08571429
77          2.8          4.8         1.4 versicolor          6.8      77 0.08571429
144         3.2          5.9         2.3  virginica          6.8     144 0.08571429
121         3.2          5.7         2.3  virginica          6.9     121 0.08571429
140         3.1          5.4         2.1  virginica          6.9     140 0.08571429
142         3.1          5.1         2.3  virginica          6.9     142 0.08571429
53          3.1          4.9         1.5 versicolor          6.9      53 0.08571429

分群的时候，我们定义了抽样3个群，随机抽出了Sepal.Length分别等于4.5，6.8，6.9的值，其他的取值就排除了本次的抽样了。

5. 系统抽样

系统抽样，先将总体的全部单元按照一定顺序排列，采用简单随机抽样抽取第一个样本单元(或称为随机起点)，再顺序抽取其余的样本单元，以固定的采样间隔进行选择，这类抽样方法被称为系统抽样。

我们可以使用UPsystematic()函数进行系统抽样的实现。我们以Sepal.Length列为抽样判断的列，先计算出每个总体单元的入样概率，为每个值被选为样本的概率。

# 取样本15个
> s <- 15

# 计算Sepal.Length的值出现概率，入样概率
> pik <-inclusionprobabilities(iris$Sepal.Length,s);pik
> pik
  [1] 0.08727895 0.08385625 0.08043354 0.07872219 0.08556760 0.09241301 0.07872219 0.08556760
  [9] 0.07529949 0.08385625 0.09241301 0.08214489 0.08214489 0.07358813 0.09925841 0.09754706
 [17] 0.09241301 0.08727895 0.09754706 0.08727895 0.09241301 0.08727895 0.07872219 0.08727895
 [25] 0.08214489 0.08556760 0.08556760 0.08899030 0.08899030 0.08043354 0.08214489 0.09241301
 [33] 0.08899030 0.09412436 0.08385625 0.08556760 0.09412436 0.08385625 0.07529949 0.08727895
 [41] 0.08556760 0.07701084 0.07529949 0.08556760 0.08727895 0.08214489 0.08727895 0.07872219
 [49] 0.09070165 0.08556760 0.11979464 0.10952653 0.11808329 0.09412436 0.11123788 0.09754706
 [57] 0.10781517 0.08385625 0.11294923 0.08899030 0.08556760 0.10096977 0.10268112 0.10439247
 [65] 0.09583571 0.11466058 0.09583571 0.09925841 0.10610382 0.09583571 0.10096977 0.10439247
 [73] 0.10781517 0.10439247 0.10952653 0.11294923 0.11637193 0.11466058 0.10268112 0.09754706
 [81] 0.09412436 0.09412436 0.09925841 0.10268112 0.09241301 0.10268112 0.11466058 0.10781517
 [89] 0.09583571 0.09412436 0.09412436 0.10439247 0.09925841 0.08556760 0.09583571 0.09754706
 [97] 0.09754706 0.10610382 0.08727895 0.09754706 0.10781517 0.09925841 0.12150599 0.10781517
[105] 0.11123788 0.13006275 0.08385625 0.12492869 0.11466058 0.12321734 0.11123788 0.10952653
[113] 0.11637193 0.09754706 0.09925841 0.10952653 0.11123788 0.13177410 0.13177410 0.10268112
[121] 0.11808329 0.09583571 0.13177410 0.10781517 0.11466058 0.12321734 0.10610382 0.10439247
[129] 0.10952653 0.12321734 0.12664005 0.13519681 0.10952653 0.10781517 0.10439247 0.13177410
[137] 0.10781517 0.10952653 0.10268112 0.11808329 0.11466058 0.11808329 0.09925841 0.11637193
[145] 0.11466058 0.11466058 0.10781517 0.11123788 0.10610382 0.10096977

# 入参概率合计为样本数
> sum(pik)
[1] 15

使用系统抽样的方法，进行抽样。

# 打印抽样的索引序号
> s6<-UPsystematic(pik);s6
  [1] 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
 [49] 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0
 [97] 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0
[145] 0 0 0 0 0 0

# 打印抽样的结果
> g6<-getdata(iris,s6);g6
    ID_unit Sepal.Length Sepal.Width Petal.Length Petal.Width    Species
2         2          4.9         3.0          1.4         0.2     setosa
15       15          5.8         4.0          1.2         0.2     setosa
26       26          5.0         3.0          1.6         0.2     setosa
37       37          5.5         3.5          1.3         0.2     setosa
49       49          5.3         3.7          1.5         0.2     setosa
59       59          6.6         2.9          4.6         1.3 versicolor
69       69          6.2         2.2          4.5         1.5 versicolor
78       78          6.7         3.0          5.0         1.7 versicolor
88       88          6.3         2.3          4.4         1.3 versicolor
98       98          6.2         2.9          4.3         1.3 versicolor
108     108          7.3         2.9          6.3         1.8  virginica
117     117          6.5         3.0          5.5         1.8  virginica
125     125          6.7         3.3          5.7         2.1  virginica
134     134          6.3         2.8          5.1         1.5  virginica
143     143          5.8         2.7          5.1         1.9  virginica

系统抽样比简单随机抽样更加方便，但可能存在某种潜在模式，会导致抽样结果是有偏差的。

6. PPS抽样和Brewer抽样

PPS抽样，是按概率比例抽样，在多阶段抽样中，尤其是二阶段抽样中，初级抽样单位被抽中的机率取决于其初级抽样单位的规模大小，初级抽样单位规模越大，被抽中的机会就越大，初级抽样单位规模越小，被抽中的机率就越小。就是将总体按一种准确的标准划分出容量不等的具有相同标志的单位在总体中不同比率分配的样本量进行的抽样。

PPS抽样，总体中含量大的部分被抽中的概率也大，可以提高样本的代表性。PPS抽样的主要优点是使用了辅助信息，减少抽样误差；主要缺点是对辅助信息要求较高，方差的估计较复杂等。PPS抽样为有放回抽样，Brewer抽样为无放回抽样。

我们先进行PPS抽样，使用UPmultinomial()函数，PPS抽样是有放回的，抽样的索引号大于1的值时为，表示被抽到多次。

# 取15个样本，定义样本的入样概率
> s <-15
> pik <-inclusionprobabilities(iris$Sepal.Length,s)

# PPS抽样，打印索引
> s7 <- UPmultinomial(pik);s7
  [1] 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0
 [49] 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 2 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0
 [97] 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0
[145] 0 0 0 0 0 0

# 查看抽样结果
> getdata(iris,s7)
     Sepal.Length Sepal.Width Petal.Length Petal.Width    Species
11            5.4         3.7          1.5         0.2     setosa
46            4.8         3.0          1.4         0.3     setosa
52            6.4         3.2          4.5         1.5 versicolor
63            6.0         2.2          4.0         1.0 versicolor
72            6.1         2.8          4.0         1.3 versicolor
72.1          6.1         2.8          4.0         1.3 versicolor
74            6.1         2.8          4.7         1.2 versicolor
88            6.3         2.3          4.4         1.3 versicolor
95            5.6         2.7          4.2         1.3 versicolor
104           6.3         2.9          5.6         1.8  virginica
114           5.7         2.5          5.0         2.0  virginica
115           5.8         2.8          5.1         2.4  virginica
118           7.7         3.8          6.7         2.2  virginica
126           7.2         3.2          6.0         1.8  virginica
142           6.9         3.1          5.1         2.3  virginica

Brewer抽样使用UPbrewer()函数，Brewer抽样是无放回的，样本不会被抽到多次。

> # Brewer抽样
> s8 <- UPbrewer(pik);s8
  [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0
 [49] 1 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0
 [97] 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
[145] 0 0 0 0 0 0
> getdata(iris,s8)
    ID_unit Sepal.Length Sepal.Width Petal.Length Petal.Width    Species
19       19          5.7         3.8          1.7         0.3     setosa
22       22          5.1         3.7          1.5         0.4     setosa
31       31          4.8         3.1          1.6         0.2     setosa
41       41          5.0         3.5          1.3         0.3     setosa
49       49          5.3         3.7          1.5         0.2     setosa
59       59          6.6         2.9          4.6         1.3 versicolor
63       63          6.0         2.2          4.0         1.0 versicolor
75       75          6.4         2.9          4.3         1.3 versicolor
89       89          5.6         3.0          4.1         1.3 versicolor
104     104          6.3         2.9          5.6         1.8  virginica
105     105          6.5         3.0          5.8         2.2  virginica
116     116          6.4         3.2          5.3         2.3  virginica
119     119          7.7         2.6          6.9         2.3  virginica
124     124          6.3         2.7          4.9         1.8  virginica
128     128          6.1         3.0          4.9         1.8  virginica

本文对于抽样技术的介绍，算是起了一个头，借助R语言可以非常方便的上手实现。抽样的好坏和实际工作量是有直接的关系，用科学的抽样方法，让抽样更准确。下一篇文章，我将继续介绍抽样估计，科学地得出抽样结论，请参考抽样三步曲之二：用R语言进行抽样估计。

转载请注明出处：
http://blog.fens.me/r-sampling

This entry was posted in R语言实践