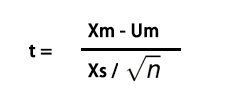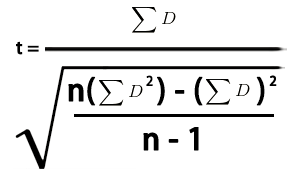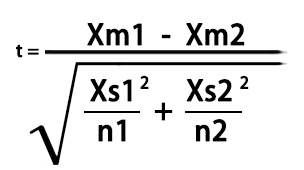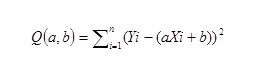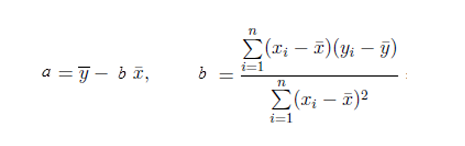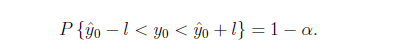R的极客理想系列文章,涵盖了R的思想,使用,工具,创新等的一系列要点,以我个人的学习和体验去诠释R的强大。
R语言作为统计学一门语言,一直在小众领域闪耀着光芒。直到大数据的爆发,R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入,R语言的社区在迅速扩大成长。现在已不仅仅是统计领域,教育,银行,电商,互联网….都在使用R语言。
要成为有理想的极客,我们不能停留在语法上,要掌握牢固的数学,概率,统计知识,同时还要有创新精神,把R语言发挥到各个领域。让我们一起动起来吧,开始R的极客理想。
关于作者:
- 张丹(Conan), 程序员/Quant: Java,R,Nodejs
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-test-t
前言
做统计分析R语言是最好的,R语言对于统计检验有非常好的支持。我会分7篇文章,分别介绍用R语言进行统计量和统计检验的计算过程,包括T检验,F检验,卡方检验,P值,KS检验,AIC,BIC等常用的统计检验方法和统计量。
本文先从T检验开始说起!
目录
- T检验介绍
- 数据集
- 单总体T检验
- 双总体T检验
1. T检验介绍
T检验,也称 student t检验(Student’s t test),是戈斯特为了观测酿酒质量发明的。戈斯特于1908年在Biometrika上公布T检验,但因其老板认为其为商业机密而被迫使用笔名(学生)。
T检验,是用于检验两个小样本的平均值差异程度的检验方法,样本量在3-30个左右,要求样本为正态分布,但总体标准差可未知。T检验,是用T分布理论来推断差异发生的概率,从而判定两个样本平均值的差异是否显著。T检验可分为单总体T检验,双总体非配对T检验,和双总体配对T检验。下面将分别进行介绍。
2. 数据集
T检验,对于数据有比较严格的要求,所以我们需要先找到一个合适的数据集,作为测试数据集。我发现了R语言自带的一个数据集sleep,是很好的测试数据集,本文接下来的内容,将以这个数据集进行测试,来介绍T检验。
开发环境所使用的系统环境
- Win10 64bit
- R: 3.4.2 x86_64-w64-mingw32/x64 b4bit
数据集,记录了10名患者使用两种催眠药物影响的对比数据,共3列,20条记录。
- extra列,为睡眠时间的变化
- group列,为药物编号
- ID列,为患者编号
查看数据集。
> data(sleep)
> sleep
extra group ID
1 0.7 1 1
2 -1.6 1 2
3 -0.2 1 3
4 -1.2 1 4
5 -0.1 1 5
6 3.4 1 6
7 3.7 1 7
8 0.8 1 8
9 0.0 1 9
10 2.0 1 10
11 1.9 2 1
12 0.8 2 2
13 1.1 2 3
14 0.1 2 4
15 -0.1 2 5
16 4.4 2 6
17 5.5 2 7
18 1.6 2 8
19 4.6 2 9
20 3.4 2 10
由于T检验的前提条件,总体要符合正态分布,只是总体方差未知。所以,我们需要先对选定数据集进行进行正态分布检验。使用Shapiro-Wilk和qq图,作为正态分布检验的方法。
Shapiro-Wilk正态分布检验: 用来检验是否数据符合正态分布,类似于线性回归的方法一样,是检验其于回归曲线的残差。该方法推荐在样本量很小的时候使用,样本在3到5000之间。该检验原假设为H0:数据集符合正态分布,统计量为W。统计量W最大值是1,越接近1,表示样本与正态分布匹配。p值,当p-value小于显著性水平α(0.05),则拒绝H0。
> shapiro.test(sleep$extra) # 总体正态分布
Shapiro-Wilk normality test
data: sleep$extra
W = 0.94607, p-value = 0.3114
检验结果,W接近1,p-value>0.05,不能拒绝原假设,所以数据集sleep是符合正态分布的。
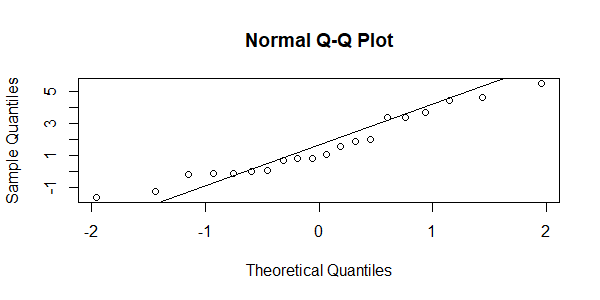
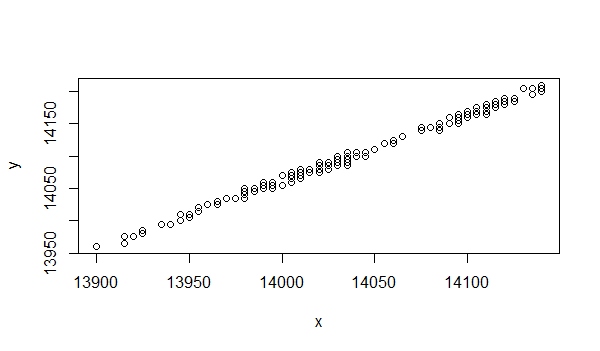
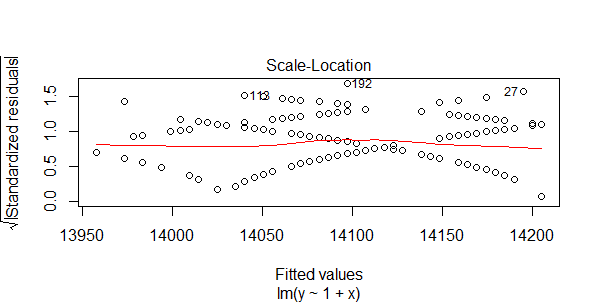
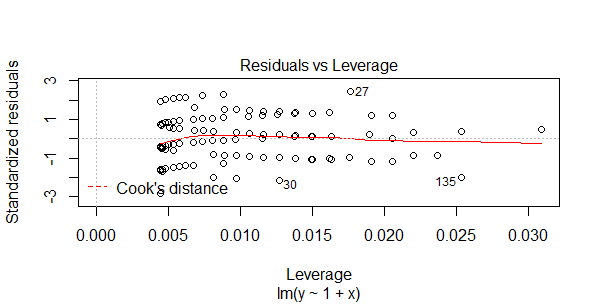
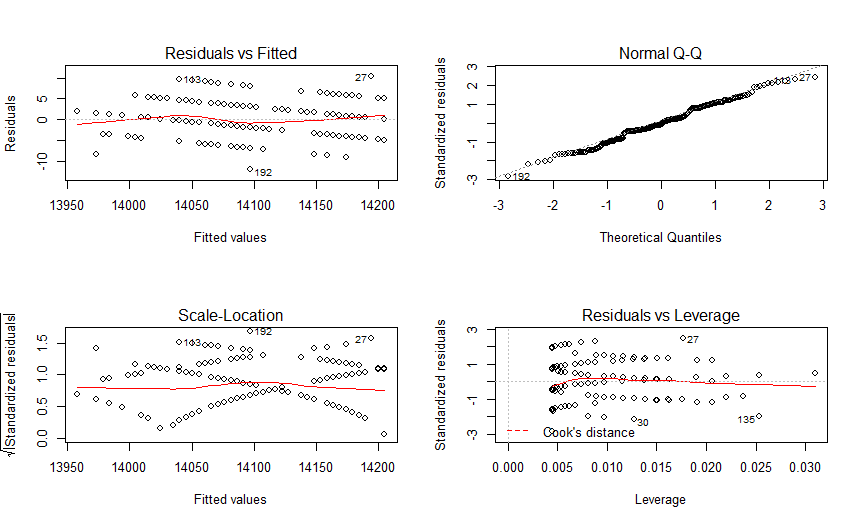
接下来,我们再画出qq图,直观的看一下数据符合正态分布的情况。
图中,对角线基本能穿过数据点,也说明数据符合正态分布。
3. 单总体的T检验
目的:单总体T检验,是检验一个样本平均值与一个已知的总体平均值的差异是否显著。当总体分布是正态分布,如总体标准差未知且样本容量较小,那么样本平均数与总体平均数的离差统计量呈t分布。
适用条件:
- 已知总体均值Um
- 可得到样本均值Xm,及该样本标准误差Xs
- 样本来自正态或近似正态总体
计算公式:T统计量
公式解释:
- Xm:样本均值
- Um:总体均值
- Xs:样本标准差
- n:样本个数
- 自由度:df=n-1
用R语言进行T检验,取sleep数据集做为总体,符合正态分布,总体平均值为1.54,以group=1为样本组,共10条记录,样本均值为0.75,样本标准差为1.78901。判断group=1分组的药物,是否有显著性改进睡眠?
# 总体均值
> Um<-mean(sleep$extra)
# 取group=1的样本组
> g1<-sleep$extra[which(sleep$group==1)]
# 计算样本均值,方差,数量
> Xm<-mean(g1)
> Xs<-sd(g1)
> n<-length(g1)
# 进行T检验
> t.test(g1,mu=Um)
One Sample t-test
data: g1
t = -1.3964, df = 9, p-value = 0.1961
alternative hypothesis: true mean is not equal to 1.54
95 percent confidence interval:
-0.5297804 2.0297804
sample estimates:
mean of x
0.75
指标解释:
- H0:原假设总体和样本均值无显著差异
- t统计量:-1.3964
- df,自由度,10-1=9
- p-value值:0.1961
- 95 percent confidence interval:95%的置信区间
- mean:样本均值0.75
结果解读,以0.05为显著性水平,t=-1.3964小于临界值2.228(查表),t值不显著,不能拒绝原假设。以0.05为显著性水平,p-value=0.19大于0.05,不能拒绝原假设,group=1的药物对睡眠没有明显改进。
我们可以用t值进行显著性差异判断,也可以用p值进行显著性差异判断,他们的作用是一样的。t值判断时,需要用计算所得的t值,与显著性水平查表对比。p值相当于是把t值,进行一种标准化的变型,只和已经定义好的显著性水平比就行了,比如0.05, 0.01, 0.001等几个固定值。
手动计算T值和P值,关于P值的详细解释,请查看文章R语言实现统计检验-P值
# 手动计算T值
> t_stat<-(Xm-Um) / (Xs/(sqrt(n)));t_stat
[1] -1.396415
# 手动计算P值
> p_value<-2*pt(-abs(t_stat),df=n-1);p_value
[1] 0.1960699
4. 双总体T检验
双总体T检验,是检验两个样本平均值,与其各自所代表的总体的差异是否显著。双总体T检验又分为两种情况,一种是配对的样本T检验,用于检验两种同质对象,在不同条件下所产生的数据差异性;另一种是独立样本非配对T检验,用于检验两组独立的样本的平均数差异性。
4.1 配对T检验
目标:检验两组同质样本,在不同的处理下的样本平均值,是否有显著的差异性。
配对设计:将2组样本的某些重要特征按相近的原则配成对子,消除混杂因素的影响,观察样本之间的处理因素和研究因素的差异,其它因素基本相同,把配对两组样本个体随机处理。
配对过程如下3种情况:
- 两种同质样本,分别接受两种不同的处理,如性别、年龄、体重、病情程度相同进行配对。
- 同一样本或同一样本的两个部分,分别接受两种不同的处理。
- 同一样本自身对比,把同一组样本处理前后的结果进行比较。
计算公式:
公式解释:
- D:两个样本差值
- εD:求和
- ε(D^2):平方和
- n:样本个数
- 自由度:df=n-1
使用sleep数据集,按group分成2个组,形成配对的数据集。H0原假设,g1和g2两个样本组均值没有显著性差异,对治疗睡眠的效果是一致的。
# 配对T检验
> t.test(extra ~ group, data = sleep, paired = TRUE)
Paired t-test
data: extra by group
t = -4.0621, df = 9, p-value = 0.002833
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-2.4598858 -0.7001142
sample estimates:
mean of the differences
-1.58
结果解读,以0.05为显著性水平,p-value=0.002833<0.05,说明g1和g2有显著性的差异,可以拒绝原假设。
接下来,我们动手自己算一下T值
# 生成数据集
> g1<-sleep$extra[which(sleep$group==1)]
> g2<-sleep$extra[which(sleep$group==2)]
# 配对T检验,与上面的计算结果是一致的
> t.test(g1,g2,paired=TRUE)
Paired t-test
data: g1 and g2
t = -4.0621, df = 9, p-value = 0.002833
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-2.4598858 -0.7001142
sample estimates:
mean of the differences
-1.58
# 动手计算
> n1<-length(g1)
> n2<-length(g2)
> D<-g1-g2
> Ds<-sum(D)
# 计算T值
> Ds/sqrt((n1*sum(D^2)-sum(D)^2)/(n1-1))
[1] -4.062128
4.2 非配对T检验
目标:用于检验两组独立的样本的平均数差异性。
- n1 和n2 为两样本容量
- Xm1和Xm2为两样本均值
- Xs1和Xs2为两样本的标准差
继续使用sleep数据集,按group分成2个组,形成独立的样本,病人按随机进行配对,去掉关联关系。H0原假设,随机选取g1和g2两个样本组均值没有显著性差异,对治疗睡眠的效果是一致的。
> t.test(extra ~ group, data = sleep)
Welch Two Sample t-test
data: extra by group
t = -1.8608, df = 17.776, p-value = 0.07939
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-3.3654832 0.2054832
sample estimates:
mean in group 1 mean in group 2
0.75 2.33
结果解读,以0.05为显著性水平,p-value=0.07939>0.05,说明g1和g2有没显著性的差异,不能拒绝原假设,两种方法对于治疗效果是一致的。
接下来,我们动手自己算一下T值。
# 计算数量,均值,标准差
> n1<-length(g1)
> n2<-length(g2)
> Xm1<-mean(g1)
> Xm2<-mean(g2)
> Xs1<-sd(g1)
> Xs2<-sd(g2)
# 计算T值
> (Xm1-Xm2)/sqrt((Xs1^2/n1)+(Xs2^2/n2))
[1] -1.860813
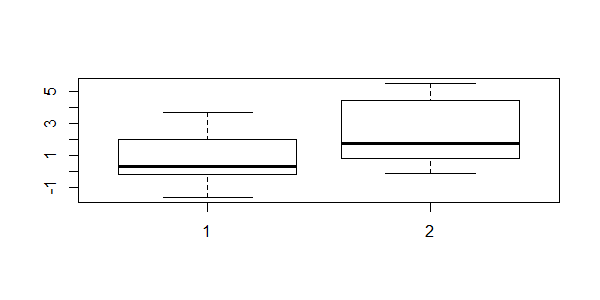
画出箱线图,观察两组数据的均值。
> boxplot(extra~group,data=sleep)
以双总体进行T检验,当是样本是配对时,g1和g2有显著性差异;而当样本是独立时,g1和g2没有显著性差异。由于我们变化了初始的假设,是会很大的程度影响统计结果的,所以在使用统计学模型时,要做非常严格的条件判断,从而保证结果的可靠性,可解释性。
转载请注明出处:
http://blog.fens.me/r-test-t