Blog Archives

Posted:

Oct 10, 2020

Tags:

Comments:

AI-900认证考试攻略

架构师的信仰系列文章，主要介绍我对系统架构的理解，从我的视角描述各种软件应用系统的架构设计思想和实现思路。

从程序员开始，到架构师一路走来，经历过太多的系统和应用。做过手机游戏，写过编程工具；做过大型Web应用系统，写过公司内部CRM；做过SOA的系统集成，写过基于Hadoop的大数据工具；做过外包，做过电商，做过团购，做过支付，做过SNS，也做过移动SNS。以前只用Java，然后学了PHP，现在用R和Javascript。最后跳出IT圈，进入金融圈，研发量化交易软件。

架构设计就是定义一套完整的程序规范，坚持架构师的信仰，做自己想做的东西。

关于作者：

张丹，分析师/程序员/Quant: R,Java,Nodejs
blog: http://fens.me
email: bsspirit@gmail.com

转载请注明出处：
http://blog.fens.me/certificate-ai900/

前言

刚考完AZ-900的考试，还在感叹Azure生态的强大，不管是架构上和还是功能上的。本来想休息一下，现在又有了新的契机，可以继续完成AI-900的认证课程。虽然AI-900的课程还是属于入门级的，却能让我更多的了解微软的产品体系和产品规划的思路，我觉得比实际做具体的代码开发，或者功能实现更有意义。关于AZ-900的考试详细介绍，请参考文章AZ-900认证考试攻略。

坚持学习，顺利通过考试。

考试契机
学习路径
复习准备

1. 考试契机

为了参加智子学院的“MCP导师认证计划”，以微软认证专家的身份，为企业提供技术咨询服务。智子学院要求参与者必须在1个自然月内完成AI-900 Azure AI Fundamentals的认证考试，同时智子学陆院免费提供考试券。有了这样的一个要求，自然地就开始了学习的过程。

客观地说，微软的Azure相关技术体系确实庞大，如果没有深入去学习这些知识，真的无从下手用微软产品。而且更难得的是，微软的docs文档条理清楚，每个技术点都有详细的介绍，不仅有技术细节，架构的描述，还有从社会意义角度的说明，真是非常有心。让我学习在过程中，不仅是知识的学习，还有对于产品规划的认识。

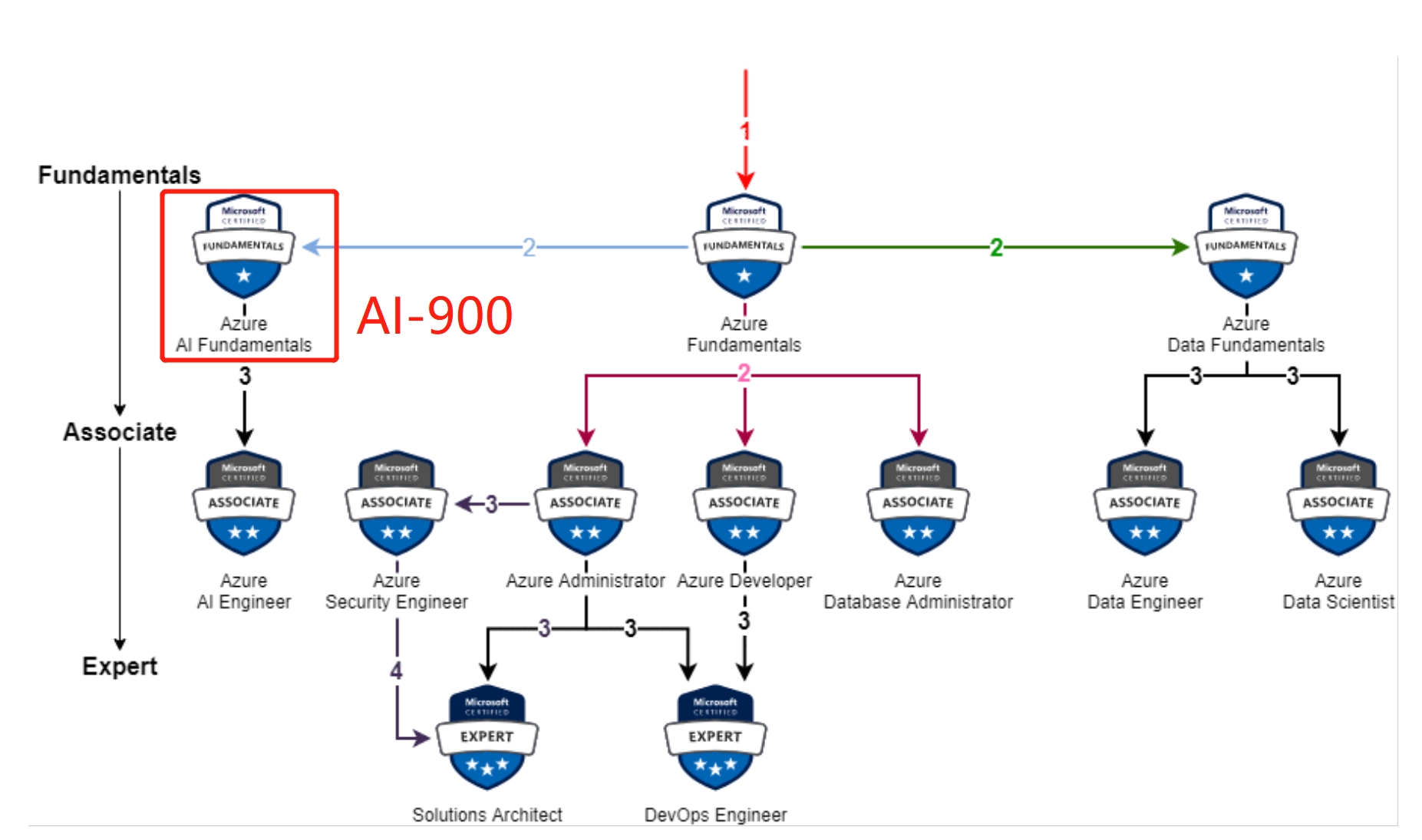
微软认证体系：

考试完成后，会获得一份考试能力评估表，来告诉你哪部分做的好，哪部分做的不好。我考试的能力评估表：我考了830分(700通过)，总体来说还是不错的成绩。

最后，就获得的证书电子版的证书 Microsoft Certified: Azure AI Fundamentals。

2. 学习路径

Microsoft Certified: Azure AI Fundamentals ，AI-900认证考试是Azure AI的基础使用的认证，包括机器学习和深度学习等智能算法，在结构化数据、图片、文字和语音的应用，主要涉及5大部分内容。

描述 AI 工作负荷和注意事项
描述 Azure 上机器学习的基本原理
描述 Azure 上的计算机视觉工作负荷的功能
描述 Azure上自然语言处理（NLP）工作负荷的特性
描述 Azure 上的对话式 AI 工作负荷的功能

微软docs上，给出了AI-900完整的学习路径，https://docs.microsoft.com/zh-cn/learn/certifications/azure-ai-fundamentals

学习大纲
第一部分：描述 AI 工作负荷和注意事项
人工智能 (AI) 为令人惊异的新的解决方案和体验赋能，Microsoft Azure 提供了易用的服务来帮助你入门。

1.1 Azure 上的 AI 入门

第二部分：描述 Azure 上机器学习的基本原理
机器学习是人工智能的核心，很多新式应用程序和服务都依赖于预测机器学习模型。了解如何使用 Azure 机器学习在不编写代码的情况下创建和发布模型。

2.1 使用 Azure 机器学习中的自动化机器学习
2.2 使用 Azure 机器学习设计器创建回归模型
2.3 使用 Azure 机器学习设计器创建分类模型
2.4 使用 Azure 机器学习设计器创建聚类分析模型

第三部分：描述 Azure 上的计算机视觉工作负荷的功能
计算机视觉是人工智能 (AI) 的一个领域，在该领域中，软件系统旨在通过摄像头、图像和视频以可视方式感知这个世界。 AI 工程师和数据科学家可以通过混合使用自定义机器学习模型和平台即服务 (PaaS) 解决方案（包括 Microsoft Azure 中的众多认知服务），来解决多种特定类型的计算机视觉问题。

3.1 使用计算机视觉服务分析图像
3.2 使用自定义视觉服务对图像进行分类
3.3 使用自定义视觉服务检测图像中的对象
3.4 使用人脸服务检测和分析人脸
3.5 使用计算机视觉服务读取文本
3.6 利用“表单识别器”服务分析收据

第四部分：描述 Azure上自然语言处理（NLP）工作负荷的功能
自然语言处理功能支持能看到用户、听到用户的声音、与用户交谈和理解用户的意图的应用程序。凭借文本分析、翻译和语言理解服务，Microsoft Azure 让你能够轻松构建支持自然语言的应用程序。

4.1 使用文本分析服务分析文本
4.2 识别和合成语音
4.3 翻译文本和语音
4.4 使用“语言理解”创建语言模型

第五部分：描述 Azure 上的对话式 AI 工作负荷的功能
对话式 AI 是一种人工智能工作负载，它可处理 AI 代理与人类用户之间的对话。

5.1 使用 QnA Maker 和 Azure 机器人服务构建机器人

学习的内容很有意思，与我目前的工作有大量的交集。我们在用R语言进行独立开发和实现的，也可以通过本次的学习，看看如果能利用微软的产品，来完成复杂的机器学习的任务。

3. 复习准备

虽然，微软docs已经有了完整的学习大纲，真学起来还是要花点时间的，重点就在于名词解释。没想到在Azure AI里体系里，定义这么多的产品和新名词。虽然我已经用过了各种云的服务和产品，但对于全面的AI产品也并不是太了解，所以借着这次考认证，正好是全面的学习。

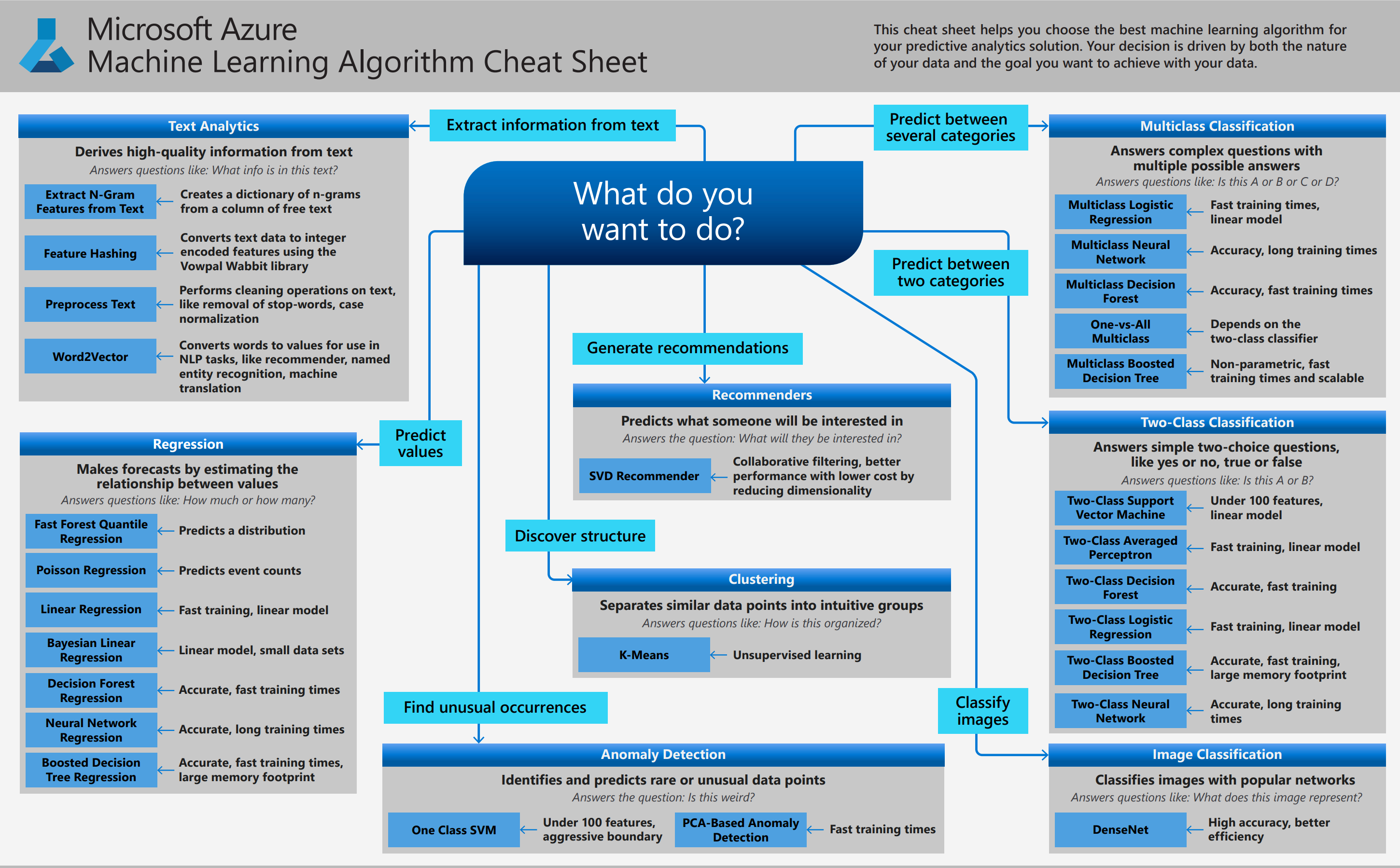
Azure机器学习算法备忘单，用于Azure的机器学习设计器，Azure 机器学习包含来自分类、推荐系统、聚类、异常检测、回归和文本分析系列的大型算法库。每个都旨在解决不同类型的机器学习问题。

3.1 名字解释
下面开始，名词解释：

Azure Machine Learning designer，Azure机器学习设计器使您可以在交互式画布上直观地连接数据集和模块，以创建机器学习模型。

Resource: Pipelines，Datasets，Compute resources，Registered models，Published pipelines，Real-time endpoints

可以使用的云资源：计算实例：数据科学家可用于处理数据和模型的开发工作站。计算群集：用于按需处理试验代码的可扩展虚拟机群集。推理群集：使用已训练模型的预测服务的部署目标。

Computer Vision :基于云的Computer Vision API使开发人员可以访问用于处理图像和返回信息的高级算法。通过上传图像或指定图像URL，Microsoft Computer Vision算法可以根据输入和用户选择以不同方式分析视觉内容。通过快速入门，教程和示例，学习如何以不同的方式分析视觉内容。

Azure Custom Vision用户自定义图像识别服务，可让您构建，部署和改进自己的图像标识符。图像标识符根据图像的视觉特征将标签（代表类或对象）应用于图像。与Computer Vision服务不同，Custom Vision允许您指定标签并训练自定义模型以检测它们。

Facial recognition: 将面部识别功能嵌入到您的应用中，以提供无缝且高度安全的用户体验。不需要机器学习专业知识。功能包括：人脸检测，可感知图像中的人脸和属性；与您最多100万人的私人存储库中的个人匹配的个人标识；感知到的情感识别，可以检测到各种面部表情，例如幸福，轻蔑，中立和恐惧；以及图像中相似面孔的识别和分组。

Optical Character recognition(OCR): 光学字符识别，该功能可从图像中提取打印或手写的文本。您可以从图像中提取文本，例如车牌照片或带有序列号的容器，以及文档（发票，账单，财务报告，物品等）中的文本。

Object detection : 对象检测类似于标记，但是API返回找到的每个对象的边界框坐标（以像素为单位）。例如，如果图像包含狗，猫和人，则“检测”操作将列出这些对象及其在图像中的坐标。您可以使用此功能来处理图像中对象之间的关系。它还使您可以确定图像中是否存在同一标签的多个实例。

Text Analytics:一种AI服务，可在非结构化文本中发现洞察力，例如情感，实体和关键短语

Natural Language Processing(NLP):自然语言处理（NLP）用于执行诸如情感分析，主题检测，语言检测，关键词提取和文档分类之类的任务。NLP可用于对文档进行分类，例如将文档标记为敏感或垃圾邮件。 NLP的输出可用于后续处理或搜索。 NLP的另一个用途是通过识别文档中存在的实体来汇总文本。这些实体还可以用于用关键字标记文档，从而可以基于内容进行搜索和检索。实体可以合并为主题，摘要描述每个文档中存在的重要主题。检测到的主题可以用于对文档进行分类以进行导航，或者在给定所选主题的情况下枚举相关文档。 NLP的另一种用途是对文本进行情感评分，以评估文档的正面或负面基调。

Key phrase extraction : 关键短语提取技能可评估非结构化文本，并为每条记录返回关键短语列表。

Named Entity Recognition(NER): 命名实体识别（NER）是在文本中标识不同实体并将其分类为预定义类或类型的能力，例如：人员，位置，事件，产品和组织。

Sentiment Analysis：情感分析功能，可评估文本并返回每个句子的情感分数和标签。这对于检测社交媒体，客户评论，论坛等中的正面和负面情绪很有用。

Translator:转换器是基于云的机器翻译服务，并且是用于构建智能应用程序的Azure认知服务认知API系列的一部分。转换器易于集成到您的应用程序，网站，工具和解决方案中。它使您可以添加70多种语言的多语言用户体验，并且可以在具有任何操作系统的任何硬件平台上用于文本翻译。

Language Detection：语言检测技能可检测输入文本的语言，并针对请求提交的每个文档报告一个语言代码。语言代码与指示分析强度的分数配对。

Speech recognition and speech synthesis:语音识别和合成样本，语音识别确实是一种令人称奇的人类能力，尤其是当您认为正常对话需要每秒识别10到15个音素时。事实证明，尝试制造机器（计算机）识别系统很困难。另一方面，各种语音合成系统已经使用了一段时间。尽管功能有限且通常缺乏人类语音的自然质量，但这些系统现在已成为我们生活中的常见组成部分。

Classification : 分类，是一种机器学习方法，它使用数据来确定项目或数据行的类别，类型或类别。例如，您可以使用分类来：将电子邮件过滤器分类为垃圾邮件，垃圾邮件或良品。确定患者的实验室样本是否癌变。根据客户对销售活动的响应倾向对其进行分类，确定情绪是正面还是负面。

Regression : 回归，是一种广泛用于从工程到教育的领域的方法。例如，您可以使用回归来基于区域数据来预测房屋的价值，或者创建有关未来入学人数的预测。

Clustering: 聚类，是一种将数据点分组为相似聚类的方法。

Cross-Validate Model: 交叉验证模型模块将带有标签的数据集以及未经训练的分类或回归模型作为输入。它将数据集划分为一定数量的子集（折叠），在每个折叠上构建模型，然后为每个折叠返回一组准确性统计信息。通过比较所有折痕的准确性统计信息，您可以解释数据集的质量并了解模型是否易受数据变化的影响。

Anomaly Detection: 异常检测，包含机器学习中的许多重要任务：确定潜在的欺诈交易。指示已发生网络入侵的学习模式。寻找异常患者群。检查输入到系统中的值。根据定义，异常是罕见事件，因此很难收集代表性的数据样本用于建模,可通过使用不平衡的数据集来解决构建和训练模型的核心挑战。

QnA Makter :QnA Maker。该认知服务支持创建和发布具有内置自然语言处理功能的知识库。可轻松在您的数据上创建自然的对话层。它可用于从您的自定义知识库（KB）信息中为任何给定的自然语言输入找到最合适的答案。使用此认知服务，你可以快速构建一个可以问答知识库，用它构成用户和 AI 代理之间对话的基础。

Azure Bot Service: 专为机器人开发而构建的托管服务
Conversation AI: 会话式AI是计算中的下一个用户界面（UI）浪潮。我们已经从必须学习和适应计算机的世界演变为现在正在学习如何理解和与我们互动的计算机。与计算机的自然交互从语言，语音和语义理解开始，并通过支持丰富的多模型交互而继续。

Language Understand (LUIS), 语言理解（LUIS）是基于云的对话式AI服务，将定制的机器学习智能应用于用户的对话式自然语言文本，以预测整体含义并提取相关的详细信息。LUIS的客户端应用程序是任何以自然语言与用户通信以完成任务的会话应用程序。客户端应用程序的示例包括社交媒体应用程序，AI聊天机器人和启用语音的桌面应用程序。

Text Analytics一种AI服务，可在非结构化文本中发现洞察力，例如情感，实体和关键短语。

Ink Recognizer: 一种AI服务，可识别数字墨水内容，例如手写，形状和墨水文档布局。

Form Recognizer: 由AI驱动的文档提取服务可以理解您的表格。

Cortana： Cortana是Microsoft的个人生产力助手，可以帮助您节省时间并将精力集中在最重要的事情上。

Principles for Responsible AI：指导AI开发和使用的六项原则：公平性，可靠性和安全性，隐私性和安全性，包容性，透明度和问责制。

Fairness: 公平性，人工智能系统应公平对待每个人，并避免以不同方式影响处境相似的人群。例如，假设你创建了一个机器学习模型来为银行的贷款审批应用程序提供支持。该模型应在不考虑任何基于性别、种族或其他因素的偏见的情况下，对是否应批准贷款做出预测，这些偏见可能导致特定的申请人群遭受不公平的差别待遇。
Reliability and safety：可靠性和保障性，AI 系统应可靠且安全地运行。例如，大家思考一下基于 AI 的自动驾驶软件系统，或诊断患者症状并推荐处方的机器学习模型这些案例。这些系统一旦出现不可靠性，就可能会给生命安全带来重大风险。
Privacy and security：隐私性和安全性，AI 系统应该保护并尊重隐私。 AI 系统所基于的机器学习模型依赖于大量数据，这些数据可能包含必须保密的个人详细信息。即使对模型进行了训练且系统已投入生产，它仍可能在使用新数据进行预测或采取行动时侵犯隐私或安全。
Inclusiveness，包容性，包容性设计实践可以帮助系统开发人员理解和解决产品环境中可能无意排除人员的潜在障碍。 AI 系统应该成为人们的有力助手，并与人互动。 AI 应不分身体能力、性别、性取向、种族或其他因素，造福社会各个阶层。
Transparency，透明度，透明度的关键部分是我们所说的可理解性，即对AI系统及其组件的行为的有用解释。要提高清晰度，就要求利益相关者理解其工作方式和原因，以便识别潜在的性能问题，安全和隐私问题，偏见，排他性做法或意想不到的结果。AI 系统应该是可理解的。应让用户能充分了解系统的用途、工作方式以及局限性。
Accountability，问责制，设计和部署AI系统的人员必须对其系统的运行方式负责。组织应借鉴行业标准来制定问责制规范。应有相关人员对 AI 系统负责。设计和开发基于 AI 的解决方案的人员应在管理和组织原则的框架内工作，以确保解决方案符合定义明确的道德和法律标准。

Azure Kubernetes Service (AKS)：Azure Kubernetes服务（AKS）使在Azure中部署托管Kubernetes群集变得简单。 AKS通过将大部分责任转移给Azure来降低管理Kubernetes的复杂性和运营开销。作为托管的Kubernetes服务，Azure可为您处理关键任务，例如运行状况监视和维护。 Kubernetes母版由Azure管理。您仅管理和维护代理节点。实时节点必须部署在AKS集群上。

3.2 模拟考试

整理完上面的名词解释，准备工作就算到位了，最后就是找份模拟题练练手。由于AI-900的认证考试是近期刚推出的，所以网上没有太多的复习资料，也没有什么攻略。

我发现的免费模拟题只有CertBolt网站上提供了，可以用 CertBolt Microsoft AI-900 模拟题库，共有55道题目。另外，在qubits42网站上有20模拟题，链接已经不能访问了。我整理成了AI模拟题PDF文件供大家下载，练习一下也就够用了。

毕竟是初级认证，考试都是基础知识，按照微软的文档进行复习准备，大概率都是可以通过的，本文的目的也是帮助大家准备考试，做到心中有底。

3.3 现场考试

最后，就是按照约好的时间，去考试中心完成考试，要带2种证明身份的证件。进到考场后，包要存起来，不能带任何东西，不能吃东西，不能喝水，不能与其他人说话等等，可以提前交卷。交卷后，找工作人员，拿到考试评估单，就可以回家庆祝了。与AZ-900的现场考试流程一样，大家可以参考文章AZ-900认证考试攻略。

本文主要是记录一下考试的前后经历，对于IT的小伙伴们，考个认证系统地学习知识，还是很有用的。未来的成就，都是之前的积累，爆发就在未来的某个瞬间。祝大家考试顺利！

刚刚又获得一张免费考试券，下一个要考啥呢！微软会一直从知识上面鞭策我们学习。

转载请注明出处：
http://blog.fens.me/certificate-ai900/

打赏作者

Posted:

Dec 15, 2018

Tags:

hms R 时间

Comments:

0 Comments

R语言轻巧的时间包hms

R的极客理想系列文章，涵盖了R的思想，使用，工具，创新等的一系列要点，以我个人的学习和体验去诠释R的强大。

R语言作为统计学一门语言，一直在小众领域闪耀着光芒。直到大数据的爆发，R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入，R语言的社区在迅速扩大成长。现在已不仅仅是统计领域，教育，银行，电商，互联网….都在使用R语言。

要成为有理想的极客，我们不能停留在语法上，要掌握牢固的数学，概率，统计知识，同时还要有创新精神，把R语言发挥到各个领域。让我们一起动起来吧，开始R的极客理想。

关于作者：

张丹(Conan), 程序员/Quant: Java,R,Nodejs
blog: http://blog.fens.me
email: bsspirit@gmail.com

转载请注明出处：
http://blog.fens.me/r-hms/

前言
时间是数据的基本维度，是在做数据处理的时候，必须要掌握的技术。根据时间周期的不同，通常把时间分为，年、月、日、时、分、秒、毫秒等。对于年月日的数据是最常见的，也有很多的处理工具，时分秒的数据通常也会用处理日期的工具，这样有时候就不太方便。

hms包，很小很轻，专注于时、分、秒的时间数据处理。

hms包介绍
hms包的使用

1. hms包介绍

hms包，用于存储和格式化时间，基于difftime类型，使用S3的面向对象数据结构。

本文的系统环境为：

Win10 64bit
R: 3.4.2 x86_64-w64-mingw32

安装hms包，非常简单，一条命令就可以了。


~ R
> install.packages("hms")
> library(hms)

函数列表：

hms: 创建一个hms类型对象
is.hms: 判断是否是hms类型
parse_hm: 解析hm值
parse_hms: 解析hms值
round_hms：四舍五入对齐
trunc_hms：裁剪对齐
as.hms: hms泛型函数，S3类型，用于隐式调用它的继承函数
as.hms.character: character转型hms，用于as.hms的继承调用
as.hms.default: hms转型hms，用于as.hms的继承调用
as.hms.difftime：difftime转型hms，用于as.hms的继承调用
as.hms.numeric: numeric转型hms，用于as.hms的继承调用
as.hms.POSIXlt: POSIXlt转型hms，用于as.hms的继承调用
as.hms.POSIXt: POSIXt转型hms，用于as.hms的继承调用
as.character.hms: hms转型character，用于as.character的继承调用
as.data.frame.hms: hms转型data.frame，用于as.data.frame的继承调用
as.POSIXct.hms: hms转型POSIXct，用于as.POSIXct的继承调用
as.POSIXlt.hms: hms转型POSIXlt，用于as.POSIXlt的继承调用
format.hms: 格式化hms，用于format的继承调用
print.hms: 打印hms对像，用于print的继承调用

从函数列表可以看到，hms包的功能很单一，就在做数据类型和数据变型，是底层的数据结构包，设计思路与zoo包的设计思路一致。zoo包的详细介绍，请参考文章R语言时间序列基础库zoo。

hms包中，有大量的as.xxx()函数、format.hms()函数和print.hms()函数，是被用于S3类型函数继承调用的，是不需要我们在写程序的时候显示调用的。S3数据结构详细介绍，请参考文章R语言基于S3的面向对象编程

2. hms包的使用

接下来，我们找几个重点函数进行介绍。

2.1 hms()函数
hms()函数，用于创建一个hms类型的对象。
函数定义：

hms(seconds = NULL, minutes = NULL, hours = NULL, days = NULL)

hms()函数，接收4个参数，分别对应秒，分，时，日。

创建hms对象


# 创建12:34:56的时间对象
> a1<-hms(56, 34, 12);a1
12:34:56

# 创建 10日12:34:56的时间对象
> a2<-hms(56, 34, 12,10);a2
252:34:56

打印结果的第一位252=10*24+12。

2.2 is.hms: 判断是否是hms类型


# 判断是否是hms类型
> is.hms(a1)
[1] TRUE

# 查看hms类型，父类是difftime类型
> class(a1)
[1] "hms"      "difftime"

# 查看hms的属性
> attributes(a1)
$units
[1] "secs"

$class
[1] "hms"      "difftime"

# 查看hms对象的静态数据结构
> str(a1)
Classes 'hms', 'difftime'  atomic [1:1] 45296
  ..- attr(*, "units")= chr "secs"

# 查看面向对象类型
> library(pryr)
> otype(a1)
[1] "S3"

2.3 as.xxx.hms：把hms转型到其他类型


# 默认转型
> as.hms(a1)
12:34:56

# hms转型character，实际会隐式调用as.character.hms()函数
> as.character(a1)
[1] "12:34:56"

# hms转型POSIXct
> as.POSIXct(a1)
[1] "1970-01-01 12:34:56 UTC"

# hms转型POSIXlt
> as.POSIXlt(a1)
[1] "1970-01-01 12:34:56 UTC"

由于我们没有定义as.Date.hms()函数，所以as.Date()函数，不能认识hms类型的转换。


# hms转型Date
> as.Date(a1)
Error in as.Date.default(a1) : 不知如何将'a1'转换成“Date”类别
Error during wrapup: cannot open the connection

自己定义一个as.Date.hms()函数，仅用于转型实验，没有实际业务意义。


# 函数定义
> as.Date.hms<-function(hms){
+   s<-paste(Sys.Date(),' ',hms,sep="")
+   as.Date(s)
+ }

# 显示调用函数
> as.Date.hms(a1)
[1] "2018-12-14"

# 隐式调用函数
> as.Date(a1)
[1] "2018-12-14"

2.4 as.hms.xxx：把其他类型转型到hms


# 把字符串转hms
> as.hms('19:13:14')
19:13:14
# 非法时间字符串转型
> as.hms('19:78:14')
NA

# 数字转型
> as.hms(111312)
30:55:12

# 时间转型
> as.hms(Sys.time())
14:22:59.462795

# 日期转型，同样发生了错误
> as.hms(Sys.Date())
Error: Can't convert object of class Date to hms.
Error during wrapup: cannot open the connection

2.5 parse_hms()/parse_hm()字符串解析

parse_hms对字符串进行转型，对比parse_hms()与as.hms()结果一样的。


# 执行parse_hms
> parse_hms("12:34:56.789")
12:34:56.789
> as.hms("12:34:56.789")
12:34:56.789

# 执行parse_hm
> parse_hm("12:34")
12:34:00
> as.hms("12:34")
NA

打印parse_hms 函数名，查看源代码实现。


> parse_hms 
function (x) {
as.hms(as.difftime(as.character(x), format = "%H:%M:%OS",
units = "secs"))
}
>environment: namespace:hms<

parse_hms()函数，实际就是调用了as.hms()函数。

2.6 round_hms/trunc_hms
round_hms()函数，是把时间进行四舍五入对齐。


# 按秒，以5的倍数进行对齐，四舍五入
> round_hms(as.hms("12:34:51"), 5)
12:34:50
> round_hms(as.hms("12:34:54"), 5)
12:34:55
> round_hms(as.hms("12:34:56"), 5)
12:34:55
> round_hms(as.hms("12:34:59"), 5)
12:35:00

# 按秒，以60的倍数对齐
> round_hms(as.hms("12:34:56"), 60)
12:35:00

trunc_hms()函数，是把时间进行裁剪对齐。


# 按秒去掉末位，以5的倍数进行对齐
> trunc_hms(as.hms("12:34:01"), 5)
12:34:00
> trunc_hms(as.hms("12:34:44"), 5)
12:34:40
> trunc_hms(as.hms("12:34:56"), 60)
12:34:00

2.7 在data.frame中插入hms列


# 创建data.frame
> df<-data.frame(hours = 1:3, hms = hms(hours = 1:3))
> df
  hours      hms
1     1 01:00:00
2     2 02:00:00
3     3 03:00:00

# 查看df的静态结构
> str(df)
'data.frame':	3 obs. of  2 variables:
 $ hours: int  1 2 3
 $ hms  :Classes 'hms', 'difftime'  atomic [1:3] 3600 7200 10800
  .. ..- attr(*, "units")= chr "secs"

hms包很轻巧很简单，但却可以快速提高帮助我们处理时分秒数据，这些基础函数库是需要我们完全掌握和熟练运用的。

转载请注明出处：
http://blog.fens.me/r-hms/

Posted:

Aug 19, 2016

Tags:

acf ar forecast pacf R 滞后自回归

Comments:

1 Comment

R语言解读自回归模型

R的极客理想系列文章，涵盖了R的思想，使用，工具，创新等的一系列要点，以我个人的学习和体验去诠释R的强大。

关于作者：

张丹(Conan), 程序员R,Nodejs,Java
weibo：@Conan_Z
blog: http://blog.fens.me
email: bsspirit@gmail.com

转载请注明出处：
http://blog.fens.me/r-ar

前言

时间序列是金融分析中常用到的一种数据格式，自回归模型是分析时间序列数据的一种基本的方法。通过建立自回归模型，找到数据自身周期性的规律，从而帮助我们理解金融市场的发展变化。

在时间序列分析中，有一个常用的模型包括AR，MA，ARMA，ARIMA，ARCH，GARCH，他们的主要区别是适用条件不同，且是层层递进的，后面的一个模型解决了前一个模型的某个固有问题。本文以AR模型做为开始，将对时间序列分析体系，进行完整的介绍，并用R语言进行模型实现。

由于本文为非统计的专业文章，所以当出现与教课书不符的描述，请以教课书为准。本文力求用简化的语言，来介绍自回归模型的知识，同时配合R语言的实现。

自回归模型介绍
用R语言构建自回归模型
模型识别ACF/PACF
模型预测

1. 自回归模型(AR)

自回归模型(Autoregressive model)，简称AR模型，是统计上一种处理时间序列的方法，用来描述当前值与历史值之间的关系，用变量自身的历史时间数据对自身进行预测，自回归模型必须满足平稳性的要求。比如，时间序列数据集X 的历史各期数据从X1至Xt-1，假设它们为线性关系，可以对当期Xt的表现进行预测。X的当期值等于一个或数个落后期的线性组合，加常数项，加随机误差。

p阶自回归过程的公式定义：

ar-forumla

字段解释：

Xt是当期的X的表现
c是常数项
p是阶数，i为从1到p的值
φi是自相关系数
t为时间周期
εt是均值为0，标准差为δ 的随机误差，同时δ是独立于t的

对于一阶自回模型，用AR(1)来表示，简化后的公式为：

自回归是从线性回归分析中发展而来，只是把自变量x对因变量y的分析，变成自变量x对自身的分析。如果你需要了解线性回归的知识，请参考文章R语言解读一元线性回归模型。

自回归模型的限制

自回归模型是用自身的数据来进行预测，但是这种方法受到一定的限制：

必须具有平稳性，平稳性要求随机过程的随机特征不随时间变化。
必须具有自相关性，如果自相关系数(φi)小于0.5，则不宜采用，否则预测结果极不准确。
自回归只适用于预测与自身前期相关的现象，即受自身历史因素影响较大的现象。对于受其他因素影响的现象，不宜采用自回归，可以改用向量自回归模型。

平稳性时间序列的特点

平稳性要求产生时间序列Y的随机过程的随机特征不随时间变化，则称过程是平稳的；假如该随机过程的随机特征随时间变化，则称过程是非平稳的。

平稳性是由样本时间序列所得到的拟合曲线，在未来的一段期间内能顺着现有的形态能一直地延续下去；如果数据非平稳，则说明样本拟合曲线的形态不具有延续的特点，也就是说拟合出来的曲线将不符合当前曲线的形态。

随机变量Yt的均值和方差均与时间t无关
随机变量Yt和Ys的协方差只与时间差（步长）t-s有关
对于平稳时间序列在数学上有比较丰富的处理手段，非平稳的时间序列通过差分等手段转化为平稳时间序列处理

2. 用R语言构建自回归模型

了解了自回归模型的定义，我们就可以用R语言来模拟一下自回归模型的构建和计算过程。

生成一个随机游走的数据集，满足平稳性的要求。


# 随机游走的数据集
> set.seed(0)
> x<-w<-rnorm(1000)       # 生成符合正态分布N(0,1)的数据
> for(t in 2:1000) x[t]<-x[t-1]+w[t]
> tsx<-ts(x)              # 生成ts时间序列的数据集

# 查看数据集
> head(tsx,15)
 [1] 1.2629543 0.9367209 2.2665202 3.5389495 3.9535909 2.4136409
 [7] 1.4850739 1.1903534 1.1845862 3.5892396 4.3528331 3.5538238
[13] 2.4061668 2.1167053 1.8174901

> plot(tsx)            # 生成可视化图形 
> a<-ar(tsx);a         # 进行自回归建模

Call:
ar(x = tsx)

Coefficients:
     1  
0.9879  

Order selected 1  sigma^2 estimated as  1.168

数据的如图展示：

自相关系数为0.9879 ，这是一个非常强的自相关性，所以上述的数列符合自相关的特性。

R语言中ar()函数提供了多种自相关系数的估计，包括"yule-walker", "burg", "ols", "mle", "yw"，默认是用yule-walker方法，常用的方法还有最小二乘法(ols)，极大似然法(mle)。

我们用最小二乘法，来进行参数估计。


> b<-ar(tsx,method = "ols");b

Call:
ar(x = tsx, method = "ols")

Coefficients:
     1  
0.9911  

Intercept: -0.017 (0.03149) 

Order selected 1  sigma^2 estimated as  0.9906

用最小二乘法的计算结果，则自相关系统数为0.9911，截距为-0.017。只有使用最小二乘法进行参数估计的时候，才会有截距。

我们用极大似然法，来进行参数估计。


> d<-ar(tsx,method = "mle");d

Call:
ar(x = tsx, method = "mle")

Coefficients:
     1  
0.9904  

Order selected 1  sigma^2 estimated as  0.9902

用极大似然法计算结果，则自相关系统数为0.9904。对于上面3种估计方法，自相关系数的值都是很接近的。

3. 模型识别ACF/PACF

在上面的例子中，我们默认是用一阶的自回归模型AR(1)，进行程序实现的。在实际应用中，自回归模型AR时间序列的阶数P是未知的，必须根据实际数据来决定，就要对AR模型定阶数。常的方法就是利用自相关函数(ACF)和偏自相关函数(PACF)来确定自回归模型的阶数。在ACF/PACF不能确定的情况下，还需要用AIC(Aikaike info Criterion)、BIC(Bayesian information criterion)的信息准则函数来确定阶数。

自回归模型的确立过程，是通过确定阶数，参数估计，再次确定阶数的方法进行判断。自相关函数ACF，用来确定采用自回归模型是否合适。如果自相关函数具有拖尾性，则AR模型为合适模型。偏自相关函数PACF用来确定模型的阶数，如果从某个阶数之后，偏自相关函数的值都很接近0，则取相应的阶数作为模型阶数，偏自相关函数通过截尾性确定阶数。

1. 自相关函数ACF(autocorrelation function)

将一个有序的随机变量序列与其自身相比较，这就是自相关函数在统计学中的定义。每个不存在相位差的序列，都与其自身相似，即在此情况下，自相关函数值最大。如果序列中的组成部分相互之间存在相关性（不再是随机的），则由以下相关值方程所计算的值不再为零，这样的组成部分为自相关。

自相关函数反映了同一序列在不同时序的取值之间的相关程序。

ACF的公式为：

acf-forumla

字段解释

Pk,为ACF的标准误差
t,为数据集的长度
k,为滞后，取值从1到t-1，表示相距 k个时间间隔的序列值之间的相关性
Yt,为样本在t时期的值
Yt-k,为样本在t-k时期的值
μ,为样本的均值

所得的自相关值Pk的取值范围为[-1,1],1为最大正相关值，-1则为最大负相关值，0为不相关。

根据上面公式，我们可以手动计算出tsx数据集的ACF值


> u<-mean(tsx)  #均值
> v<-var(tsx)   #方差

> # 1阶滞后
> p1<-sum((x[1:length(tsx)-1]-u)*(x[2:length(tsx)]-u))/((length(tsx)-1)*v);p1
[1] 0.9878619
> # 2阶滞后
> p2<-sum((x[1:(length(tsx)-2)]-u)*(x[3:length(tsx)]-u))/((length(tsx)-1)*v);p2
[1] 0.9760271
> # 3阶滞后
> p3<-sum((x[1:(length(tsx)-3)]-u)*(x[4:length(tsx)]-u))/((length(tsx)-1)*v);p3
[1] 0.9635961

同时，我们可以用R语言中的acf()函数来计算，会打印前30个滞后的ACF值。


> acf(tsx)$acf
, , 1

           [,1]
 [1,] 1.0000000
 [2,] 0.9878619
 [3,] 0.9760271
 [4,] 0.9635961
 [5,] 0.9503371
 [6,] 0.9384022
 [7,] 0.9263075
 [8,] 0.9142540
 [9,] 0.9024862
[10,] 0.8914740
[11,] 0.8809663
[12,] 0.8711005
[13,] 0.8628609
[14,] 0.8544984
[15,] 0.8462270
[16,] 0.8384758
[17,] 0.8301834
[18,] 0.8229206
[19,] 0.8161523
[20,] 0.8081941
[21,] 0.8009467
[22,] 0.7942255
[23,] 0.7886249
[24,] 0.7838154
[25,] 0.7789733
[26,] 0.7749697
[27,] 0.7709313
[28,] 0.7662547
[29,] 0.7623381
[30,] 0.7604101
[31,] 0.7577333

比较前3个值的计算结果，与我们自己的计算结果是一样的，同时可以用R语言进行可视化输出。


> acf(tsx)

从上图中看出，数据的ACF为拖尾，存在很严重的自相关性。接下来，这时候我们用偏自相关函数确定一下AR的阶数。

2. 偏自相关函数(PACF)(partial autocorrelation function)

偏自相关函数是有自相关函数推到而来。对于一个平稳AR(p)模型，求出滞后k自相关系数p(k)时，实际上得到并不是x(t)与x(t-k)之间单纯的相关关系。因为x(t)同时还会受到中间k-1个随机变量x(t-1)、x(t-2)、……、x(t-k+1)的影响，而这k-1个随机变量又都和x(t-k)具有相关关系，所以自相关系数p(k)里实际掺杂了其他变量对x(t)与x(t-k)的影响。

为了能单纯测度x(t-k)对x(t)的影响，引进偏自相关系数的概念。对于平稳时间序列{x(t)}，所谓滞后k偏自相关系数指在给定中间k-1个随机变量x(t-1)、x(t-2)、……、x(t-k+1)的条件下，或者说，在剔除了中间k-1个随机变量x(t-1)、x(t-2)、……、x(t-k+1)的干扰之后，x(t-k)对x(t)影响的相关程度。

简单来说，就是自相关系数ACF还包含了其他变量的影响，而偏自相关系数PACF是严格这两个变量之间的相关性。在ACF中存在着线性关系和非线性关系，偏自相关函数就是把线性关系从自动关系性中消除。当PACF近似于0，表明两个时间点之间的关系性是完全由线性关系所造成的。

通过R语言的pacf()函数来进行偏自相关函数计算。


> pacf(tsx)$acf
, , 1

              [,1]
 [1,]  0.987861891
 [2,]  0.006463542
 [3,] -0.030541593
 [4,] -0.041290415
 [5,]  0.047921168
 [6,] -0.009774246
 [7,] -0.006267004
 [8,]  0.002146693
 [9,]  0.028782423
[10,]  0.014785187
[11,]  0.019307564
[12,]  0.060879259
[13,] -0.007254278
[14,] -0.004139848
[15,]  0.015707900
[16,] -0.018615370
[17,]  0.037067452
[18,]  0.019322565
[19,] -0.048471479
[20,]  0.023388065
[21,]  0.027640953
[22,]  0.051177900
[23,]  0.028063875
[24,] -0.003957142
[25,]  0.034030631
[26,]  0.004270416
[27,] -0.029613088
[28,]  0.033715973
[29,]  0.092337583
[30,] -0.031264028

# 可视化输出 
> pacf(tsx)

从上面的这个结果分析，当滞后为1时AR模型显著，滞后为其他值是PACF的值接近于0不显著。所以，对于数据集tsx来说，数据满足AR(1)的自回归模型。对于上文中参数估计出的1阶自相关系数值是可以用的。

4. 模型预测

通过模型识别，我们已经确定了数据集tsx是符合AR(1)的建模条件的，同时我们也创建了AR(1)模型。接下来，就可以利用这个自回测的模型的进行预测，通过规律发现价值。在R语言中，我们可以用predict()函数，实现预测的计算。

使用AR(1)模型进行预测，并保留前5个预测点。


> predict(a,10,n.ahead=5L)
$pred
Time Series:
Start = 2 
End = 6 
Frequency = 1 
[1] 9.839680 9.681307 9.524855 9.370303 9.217627

$se
Time Series:
Start = 2 
End = 6 
Frequency = 1 
[1] 1.080826 1.519271 1.849506 2.122810 2.359189

上面结果中，变量$pred表示预测值，变量$se为误差。

我可以生成可视化的图，更直观的看到预测的结果。


# 生成50个预测值 
> tsp<-predict(a,n.ahead=50L)

# 把原数据画图 
> plot(tsx)

# 把预测值和误差画出来
> lines(tsp$pred,col='red')                
> lines(tsp$pred+tsp$se,col='blue')
> lines(tsp$pred-tsp$se,col='blue')

图中，黑色线为原始数据的，红色线为预测值，蓝色线为预测值的范围。这样我们就利用AR(1)模型，实现了对规律的预测计算。

上面关于预测和可视化的过程,我们是通过原生的predict()函数和plot()函数完成的。在R语言中，可以用forecast包来简化上面的操作过程，让代码更少，操作更便捷。


# 加载forecast包
> library('forecast')

# 生成模型AR(1) 
> a2 <- arima(tsx, order=c(1,0,0))
> tsp2<-forecast(a2, h=50)
> plot(tsp2)

查看forecast()计算后的预测结果。


> tsp2
     Point Forecast     Lo 80      Hi 80     Lo 95       Hi 95
1001      -15.71590 -16.99118 -14.440628 -17.66627 -13.7655369
1002      -15.60332 -17.39825 -13.808389 -18.34843 -12.8582092
1003      -15.49181 -17.67972 -13.303904 -18.83792 -12.1456966
1004      -15.38136 -17.89579 -12.866932 -19.22685 -11.5358726
1005      -15.27197 -18.06994 -12.474000 -19.55110 -10.9928432
1006      -15.16362 -18.21425 -12.112996 -19.82915 -10.4980922
1007      -15.05631 -18.33593 -11.776682 -20.07206 -10.0405541
1008      -14.95001 -18.43972 -11.460312 -20.28705  -9.6129750
1009      -14.84474 -18.52891 -11.160567 -20.47919  -9.2102846
1010      -14.74046 -18.60591 -10.875013 -20.65216  -8.8287673
1011      -14.63718 -18.67257 -10.601802 -20.80877  -8.4655994
1012      -14.53489 -18.73030 -10.339486 -20.95121  -8.1185723
1013      -14.43357 -18.78024 -10.086905 -21.08123  -7.7859174
1014      -14.33322 -18.82333  -9.843112 -21.20026  -7.4661903
1015      -14.23383 -18.86034  -9.607319 -21.30947  -7.1581923
1016      -14.13538 -18.89190  -9.378864 -21.40985  -6.8609139

通过forecast()函数，直接生成了Forecast值，80%概率的预测值范围，和95%概率的预测值范围。

在明白了整个自回归模型的设计思路、建模过程、检验条件、预测计算、可视化展示的完整操作后，我们就可以真正地把自回归模型用到实际的业务中。发现规律，发现价值！！

自回归模型只是开始，下一篇继续介绍移动平均模型(MA)的建模和使用过程。

转载请注明出处：
http://blog.fens.me/r-ar

打赏作者

Posted:

Jul 27, 2016

Tags:

AIC R 多元热卷焦炭焦煤线性回归统计螺纹钢逐步回归铁矿石黑色系

Comments:

15 Comments

R语言解读多元线性回归模型

R的极客理想系列文章，涵盖了R的思想，使用，工具，创新等的一系列要点，以我个人的学习和体验去诠释R的强大。

关于作者：

张丹(Conan), 程序员R,Nodejs,Java
weibo：@Conan_Z
blog: http://blog.fens.me
email: bsspirit@gmail.com

转载请注明出处：
http://blog.fens.me/r-multi-linear-regression

前言

本文接上一篇R语言解读一元线性回归模型。在许多生活和工作的实际问题中，影响因变量的因素可能不止一个，比如对于知识水平越高的人，收入水平也越高，这样的一个结论。这其中可能包括了因为更好的家庭条件，所以有了更好的教育；因为在一线城市发展，所以有了更好的工作机会；所处的行业赶上了大的经济上行周期等。要想解读这些规律，是复杂的、多维度的，多元回归分析方法更适合解读生活的规律。

由于本文为非统计的专业文章，所以当出现与教课书不符的描述，请以教课书为准。本文力求用简化的语言，来介绍多元线性回归的知识，同时配合R语言的实现。

多元线性回归介绍
元线性回归建模
模型优化
案例：黑色系期货日K线数据验证

1. 多元线性回归介绍

对比一元线性回归，多元线性回归是用来确定2个或2个以上变量间关系的统计分析方法。多元线性回归的基本的分析方法与一元线性回归方法是类似的，我们首先需要对选取多元数据集并定义数学模型，然后进行参数估计，对估计出来的参数进行显著性检验，残差分析，异常点检测，最后确定回归方程进行模型预测。

由于多元回归方程有多个自变量，区别于一元回归方程，有一项很重要的操作就是自变量的优化，挑选出相关性最显著的自变量，同时去除不显著的自变量。在R语言中，有很方便地用于优化函数，可以很好的帮助我们来改进回归模型。

下面就开始多元线性回归的建模过程。

2. 多元线性回归建模

做过商品期货研究的人，都知道黑色系品种是具有产业链上下游的关系。铁矿石是炼钢的原材料，焦煤和焦炭是炼钢的能源资源，热卷即热轧卷板是以板坯为原料经加热后制成的钢板，螺纹钢是表面带肋的钢筋。

由于有产业链的关系，假设我们想要预测螺纹钢的价格，那么影响螺纹钢价格的因素可以会涉及到原材料，能源资源和同类材料等。比如，铁矿石价格如果上涨，螺纹钢就应该要涨价了。

2.1 数据集和数学模型

先从数据开始介绍，这次的数据集，我选择的期货黑色系的品种的商品期货，包括了大连期货交易所的焦煤(JM)，焦炭(J)，铁矿石(I)，上海期货交易所的螺纹钢(RU) 和热卷(HC)。

数据集为2016年3月15日，当日白天开盘的交易数据，为黑色系的5个期货合约的分钟线的价格数据。


# 数据集已存在df变量中
> head(df,20)
                       x1    x2    x3   x4    y
2016-03-15 09:01:00 754.5 616.5 426.5 2215 2055
2016-03-15 09:02:00 752.5 614.5 423.5 2206 2048
2016-03-15 09:03:00 753.0 614.0 423.0 2199 2044
2016-03-15 09:04:00 752.5 613.0 422.5 2197 2040
2016-03-15 09:05:00 753.0 615.5 424.0 2198 2043
2016-03-15 09:06:00 752.5 614.5 422.0 2195 2040
2016-03-15 09:07:00 752.0 614.0 421.5 2193 2036
2016-03-15 09:08:00 753.0 615.0 422.5 2197 2043
2016-03-15 09:09:00 754.0 615.5 422.5 2197 2041
2016-03-15 09:10:00 754.5 615.5 423.0 2200 2044
2016-03-15 09:11:00 757.0 616.5 423.0 2201 2045
2016-03-15 09:12:00 756.0 615.5 423.0 2200 2044
2016-03-15 09:13:00 755.5 615.0 423.0 2197 2042
2016-03-15 09:14:00 755.5 615.0 423.0 2196 2042
2016-03-15 09:15:00 756.0 616.0 423.5 2200 2045
2016-03-15 09:16:00 757.5 616.0 424.0 2205 2052
2016-03-15 09:17:00 758.5 618.0 424.0 2204 2051
2016-03-15 09:18:00 759.5 618.5 424.0 2205 2053
2016-03-15 09:19:00 759.5 617.5 424.5 2206 2053
2016-03-15 09:20:00 758.5 617.5 423.5 2201 2050

数据集包括有6列:

索引, 为时间
x1, 为焦炭(j1605)合约的1分钟线的报价数据
x2, 为焦煤(jm1605)合约的1分钟线的报价数据
x3, 为铁矿石(i1605)合约的1分钟线的报价数据
x4, 为热卷(hc1605)合约的1分钟线的报价数据
y, 为螺纹钢(rb1605)合约的1分钟线的报价数据

假设螺纹钢的价格与其他4个商品的价格有线性关系，那么我们建立以螺纹钢为因变量，以焦煤、焦炭、铁矿石和热卷的为自变量的多元线性回归模型。用公式表示为：

y = a + b * x1 + c * x2 + d * x3 + e * x4 + ε

y，为因变量，螺纹钢
x1，为自变量，焦煤
x2，为自变量，焦炭
x3，为自变量，铁矿石
x4，为自变量，热卷
a，为截距
b,c,d,e，为自变量系数
ε, 为残差，是其他一切不确定因素影响的总和，其值不可观测。假定ε服从正态分布N(0,σ^2)。

通过对多元线性回归模型的数学定义，接下来让我们利用数据集做多元回归模型的参数估计。

2.2. 回归参数估计

上面公式中，回归参数 a, b, c, d,e都是我们不知道的，参数估计就是通过数据来估计出这些参数，从而确定自变量和因变量之前的关系。我们的目标是要计算出一条直线，使直线上每个点的Y值和实际数据的Y值之差的平方和最小，即（Y1实际-Y1预测）^2+（Y2实际-Y2预测）^2+ …… +（Yn实际-Yn预测）^2 的值最小。参数估计时，我们只考虑Y随X自变量的线性变化的部分，而残差ε是不可观测的，参数估计法并不需要考虑残差。

类似于一元线性回归，我们用R语言来实现对数据的回归模型的参数估计，用lm()函数来实现多元线性回归的建模过程。


# 建立多元线性回归模型
> lm1<-lm(y~x1+x2+x3+x4,data=df)

# 打印参数估计的结果
> lm1

Call:
lm(formula = y ~ x1 + x2 + x3 + x4, data = df)

Coefficients:
(Intercept)           x1           x2           x3           x4  
   212.8780       0.8542       0.6672      -0.6674       0.4821

这样我们就得到了y和x关系的方程。

y = 212.8780 + 0.8542 * x1 + 0.6672 * x2 - 0.6674 * x3 + 0.4821 * x4

2.3. 回归方程的显著性检验

参考一元线性回归的显著性检验，多元线性回归的显著性检验，同样是需要经过 T检验，F检验，和R^2(R平方)相关系统检验。在R语言中这三种检验的方法都已被实现，我们只需要把结果解读，我们可以summary()函数来提取模型的计算结果。


> summary(lm1)

Call:
lm(formula = y ~ x1 + x2 + x3 + x4, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.9648 -1.3241 -0.0319  1.2403  5.4194 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 212.87796   58.26788   3.653 0.000323 ***
x1            0.85423    0.10958   7.795 2.50e-13 ***
x2            0.66724    0.12938   5.157 5.57e-07 ***
x3           -0.66741    0.15421  -4.328 2.28e-05 ***
x4            0.48214    0.01959  24.609  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.028 on 221 degrees of freedom
Multiple R-squared:  0.9725,	Adjusted R-squared:  0.972 
F-statistic:  1956 on 4 and 221 DF,  p-value: < 2.2e-16

T检验：所自变量都是非常显著***
F检验：同样是非常显著，p-value < 2.2e-16
调整后的R^2：相关性非常强为0.972

最后，我们通过的回归参数的检验与回归方程的检验，得到最后多元线性回归方程为：


y = 212.87796 + 0.85423 * x1 + 0.66724 * x2 - 0.66741 * x3 + 0.48214 * x4

即

螺纹钢 = 212.87796 + 0.85423 * 焦炭 + 0.66724 * 焦煤 - 0.66741 * 铁矿石 + 0.48214 * 热卷

2.4 残差分析和异常点检测

在得到的回归模型进行显著性检验后，还要在做残差分析(预测值和实际值之间的差)，检验模型的正确性，残差必须服从正态分布N(0,σ^2)。直接用plot()函数生成4种用于模型诊断的图形，进行直观地分析。


> par(mfrow=c(2,2))
> plot(lm1)

残差和拟合值(左上)，残差和拟合值之间数据点均匀分布在y=0两侧，呈现出随机的分布，红色线呈现出一条平稳的曲线并没有明显的形状特征。
残差QQ图(右上)，数据点按对角直线排列，趋于一条直线，并被对角直接穿过，直观上符合正态分布。
标准化残差平方根和拟合值(左下)，数据点均匀分布在y=0两侧，呈现出随机的分布，红色线呈现出一条平稳的曲线并没有明显的形状特征。
标准化残差和杠杆值(右下)，没有出现红色的等高线，则说明数据中没有特别影响回归结果的异常点。

结论，没有明显的异常点，残差符合假设条件。

2.5. 模型预测

我们得到了多元线性回归方程的公式，就可以对数据进行预测了。我们可以用R语言的predict()函数来计算预测值y0和相应的预测区间，并把实际值和预测值一起可视化化展示。


> par(mfrow=c(1,1))  #设置画面布局

# 预测计算
> dfp<-predict(lm1,interval="prediction")

# 打印预测时
> head(dfp,10)
                fit      lwr      upr
2014-03-21 3160.526 3046.425 3274.626
2014-03-24 3193.253 3078.868 3307.637
2014-03-25 3240.389 3126.171 3354.607
2014-03-26 3228.565 3114.420 3342.710
2014-03-27 3222.528 3108.342 3336.713
2014-03-28 3262.399 3148.132 3376.666
2014-03-31 3291.996 3177.648 3406.344
2014-04-01 3305.870 3191.447 3420.294
2014-04-02 3275.370 3161.018 3389.723
2014-04-03 3297.358 3182.960 3411.755

# 合并数据
> mdf<-merge(df$y,dfp)	 

# 画图
> draw(mdf)

图例说明

y, 实际价格，红色线
fit, 预测价格，绿色线
lwr，预测最低价，蓝色线
upr，预测最高价，紫色线

从图中看出，实际价格y和预测价格fit，在大多数的时候都是很贴近的。我们的一个模型就训练好了！

3. 模型优化

上文中，我们已经很顺利的发现了一个非常不错的模型。如果要进行模型优化，可以用R语言中update()函数进行模型的调整。我们首先检查一下每个自变量x1,x2,x3,x4和因变量y之间的关系。

pairs(as.data.frame(df))

从图中，我们可以发现x2与Y的关系，可能是最偏离线性的。那么，我们尝试对多元线性回归模型进行调整，从原模型中去掉x2变量。



# 模型调整
> lm2<-update(lm1, .~. -x2)

> summary(lm2)

Call:
lm(formula = y ~ x1 + x3 + x4, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-6.0039 -1.3842  0.0177  1.3513  4.8028 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 462.47104   34.26636   13.50  < 2e-16 ***
x1            1.08728    0.10543   10.31  < 2e-16 ***
x3           -0.40788    0.15394   -2.65  0.00864 ** 
x4            0.42582    0.01718   24.79  < 2e-16 ***
---
Signif. codes:  
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.142 on 222 degrees of freedom
Multiple R-squared:  0.9692,	Adjusted R-squared:  0.9688 
F-statistic:  2330 on 3 and 222 DF,  p-value: < 2.2e-16

当把自变量x2去掉后，自变量x3的T检验反而变大了，同时Adjusted R-squared变小了，所以我们这次调整是有问题的。

如果通过生产和原材料的内在逻辑分析，焦煤与焦炭属于上下游关系。焦煤是生产焦炭的一种原材料，焦炭是焦煤与其他炼焦煤经过配煤焦化形成的产品，一般生产 1 吨焦炭需要1.33 吨炼焦煤，其中焦煤至少占 30% 。

我们把焦煤和焦炭的关系改变一下，增加x1*x2的关系匹配到模型，看看效果。


# 模型调整
> lm3<-update(lm1, .~. + x1*x2)
> summary(lm3)

Call:
lm(formula = y ~ x1 + x2 + x3 + x4 + x1:x2, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.8110 -1.3501 -0.0595  1.2019  5.3884 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) 7160.32231 7814.50048   0.916    0.361    
x1            -8.45530   10.47167  -0.807    0.420    
x2           -10.58406   12.65579  -0.836    0.404    
x3            -0.64344    0.15662  -4.108 5.63e-05 ***
x4             0.48363    0.01967  24.584  < 2e-16 ***
x1:x2          0.01505    0.01693   0.889    0.375    
---
Signif. codes:  
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.029 on 220 degrees of freedom
Multiple R-squared:  0.9726,	Adjusted R-squared:  0.972 
F-statistic:  1563 on 5 and 220 DF,  p-value: < 2.2e-16

从结果中发现，增加了x1*x2列后，原来的x1,x2和Intercept的T检验都不显著。继续调整模型，从模型中去掉x1,x2两个自变量。


# 模型调整
> lm4<-update(lm3, .~. -x1-x2)
> summary(lm4)

Call:
lm(formula = y ~ x3 + x4 + x1:x2, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.9027 -1.2516 -0.0167  1.2748  5.8683 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  6.950e+02  1.609e+01  43.183  < 2e-16 ***
x3          -6.284e-01  1.530e-01  -4.108 5.61e-05 ***
x4           4.959e-01  1.785e-02  27.783  < 2e-16 ***
x1:x2        1.133e-03  9.524e-05  11.897  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.035 on 222 degrees of freedom
Multiple R-squared:  0.9722,	Adjusted R-squared:  0.9718 
F-statistic:  2588 on 3 and 222 DF,  p-value: < 2.2e-16

从调整后的结果来看，效果还不错。不过，也并没有比最初的模型有所提高。

对于模型调整的过程，如果我们手动调整测试时，一般都会基于业务知识来操作。如果是按照数据指标来计算，我们可以用R语言中提供的逐步回归的优化方法，通过AIC指标来判断是否需要参数优化。


#对lm1模型做逐步回归
> step(lm1)
Start:  AIC=324.51
y ~ x1 + x2 + x3 + x4

       Df Sum of Sq    RSS    AIC
               908.8 324.51
- x3    1     77.03  985.9 340.90
- x2    1    109.37 1018.2 348.19
- x1    1    249.90 1158.8 377.41
- x4    1   2490.56 3399.4 620.65

Call:
lm(formula = y ~ x1 + x2 + x3 + x4, data = df)

Coefficients:
(Intercept)           x1           x2           x3           x4  
   212.8780       0.8542       0.6672      -0.6674       0.4821

通过计算AIC指标，lm1的模型AIC最小时为324.51，每次去掉一个自变量都会让AIC的值变大，所以我们还是不调整比较好。

对刚才的lm3模型做逐步回归的模型调整。


#对lm3模型做逐步回归
> step(lm3)
Start:  AIC=325.7               #当前AIC
y ~ x1 + x2 + x3 + x4 + x1:x2

        Df Sum of Sq    RSS    AIC
- x1:x2  1      3.25  908.8 324.51
                905.6 325.70
- x3     1     69.47  975.1 340.41
- x4     1   2487.86 3393.5 622.25

Step:  AIC=324.51               #去掉x1*x2项的AIC
y ~ x1 + x2 + x3 + x4

       Df Sum of Sq    RSS    AIC
               908.8 324.51
- x3    1     77.03  985.9 340.90
- x2    1    109.37 1018.2 348.19
- x1    1    249.90 1158.8 377.41
- x4    1   2490.56 3399.4 620.65

Call:
lm(formula = y ~ x1 + x2 + x3 + x4, data = df)

Coefficients:
(Intercept)           x1           x2           x3           x4  
   212.8780       0.8542       0.6672      -0.6674       0.4821

通过AIC的判断，去掉X1*X2项后AIC最小，最后的检验结果告诉我们，还是原初的模型是最好的。

4. 案例：黑色系期货日K线数据验证

最后，我们用上面5个期货合约的日K线数据测试一下，找到多元回归关系。


> lm9<-lm(y~x1+x2+x3+x4,data=df)  # 日K线数据
> summary(lm9)

Call:
lm(formula = y ~ x1 + x2 + x3 + x4, data = df)

Residuals:
     Min       1Q   Median       3Q      Max 
-173.338  -37.470    3.465   32.158  178.982 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 386.33482   31.07729  12.431  < 2e-16 ***
x1            0.75871    0.07554  10.045  < 2e-16 ***
x2           -0.62907    0.14715  -4.275 2.24e-05 ***
x3            1.16070    0.05224  22.219  < 2e-16 ***
x4            0.46461    0.02168  21.427  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 57.78 on 565 degrees of freedom
Multiple R-squared:  0.9844,	Adjusted R-squared:  0.9843 
F-statistic:  8906 on 4 and 565 DF,  p-value: < 2.2e-16

数据集的基本统计信息。


> summary(df)
     Index                           x1               x2       
 Min.   :2014-03-21 00:00:00   Min.   : 606.5   Min.   :494.0  
 1st Qu.:2014-10-21 06:00:00   1st Qu.: 803.5   1st Qu.:613.1  
 Median :2015-05-20 12:00:00   Median : 939.0   Median :705.8  
 Mean   :2015-05-21 08:02:31   Mean   : 936.1   Mean   :695.3  
 3rd Qu.:2015-12-16 18:00:00   3rd Qu.:1075.0   3rd Qu.:773.0  
 Max.   :2016-07-25 00:00:00   Max.   :1280.0   Max.   :898.0  

       x3              x4             y       
 Min.   :284.0   Min.   :1691   Min.   :1626  
 1st Qu.:374.1   1st Qu.:2084   1st Qu.:2012  
 Median :434.0   Median :2503   Median :2378  
 Mean   :476.5   Mean   :2545   Mean   :2395  
 3rd Qu.:545.8   3rd Qu.:2916   3rd Qu.:2592  
 Max.   :825.0   Max.   :3480   Max.   :3414

对于日K线数据，黑色系的5个品种，同样具有非常强的相关关系，那么我们就可以把这个结论应用到实际的交易中了。

本文通过多元回归的统计分析方法，介绍多元回归在金融市场的基本应用。我们通过建立因变量和多个自变量的模型，从而发现生活中更复杂的规律，并建立有效的验证指标。让我们我们的技术优势，去金融市场抢钱吧。

转载请注明出处：
http://blog.fens.me/r-multi-linear-regression

打赏作者

Posted:

Jul 25, 2016

Tags:

F检验 R R^2 T检验一元截距方差相关性系数线性回归统计

Comments:

6 Comments

R语言解读一元线性回归模型

R的极客理想系列文章，涵盖了R的思想，使用，工具，创新等的一系列要点，以我个人的学习和体验去诠释R的强大。

关于作者：

张丹(Conan), 程序员R,Nodejs,Java
weibo：@Conan_Z
blog: http://blog.fens.me
email: bsspirit@gmail.com

转载请注明出处：
http://blog.fens.me/r-linear-regression/

前言

在我们的日常生活中，存在大量的具有相关性的事件，比如大气压和海拔高度，海拔越高大气压强越小；人的身高和体重，普遍来看越高的人体重也越重。还有一些可能存在相关性的事件，比如知识水平越高的人，收入水平越高；市场化的国家经济越好，则货币越强势，反而全球经济危机，黄金等避险资产越走强。

如果我们要研究这些事件，找到不同变量之间的关系，我们就会用到回归分析。一元线性回归分析是处理两个变量之间关系的最简单模型，是两个变量之间的线性相关关系。让我们一起发现生活中的规律吧。

由于本文为非统计的专业文章，所以当出现与教课书不符的描述，请以教课书为准。本文力求用简化的语言，来介绍一元线性回归的知识，同时配合R语言的实现。

一元线性回归介绍
数据集和数学模型
回归参数估计
回归方程的显著性检验
残差分析和异常点检测
模型预测

1. 一元线性回归介绍

回归分析（Regression Analysis)是用来确定2个或2个以上变量间关系的一种统计分析方法。如果回归分析中，只包括一个自变量X和一个因变量Y时，且它们的关系是线性的，那么这种回归分析称为一元线性回归分析。

回归分析属于统计学的基本模型，涉及统计学基础，就会有一大堆的名词和知识点需要介绍。

在回归分析中，变量有2类：因变量和自变量。因变量通常是指实际问题中所关心的指标，用Y表示。而自变量是影响因变量取值的一个变量，用X表示，如果有多个自变量则表示为X1, X2, …, Xn。

回归分析研究的主要步骤：

确定因变量Y 与自变量X1, X2, …, Xn 之间的定量关系表达式，即回归方程。
对回归方程的置信度检查。
判断自变量Xn(n=1,2,…,m)对因变量的影响。
利用回归方程进行预测。

本文会根据回归分析的的主要步骤，进行结构梳理，介绍一元线性回归模型的使用方法。

2. 数据集和数学模型

先让我们通过一个例子开始吧，用一组简单的数据来说明一元线性回归分析的数学模型的原理和公式。找出下面数据集中Y与X的定量关系。

数据集为2016年3月1日，白天开盘的交易数据，为锌的2个期货合约的分钟线的价格数据。数据集包括有3列，索引列为时间，zn1.Close为ZN1604合约的1分钟线的报价数据，zn2.Close为ZN1605合约的1分钟线的报价数据。

数据集如下：


                    zn1.Close zn2.Close
2016-03-01 09:01:00     14075     14145
2016-03-01 09:02:00     14095     14160
2016-03-01 09:03:00     14095     14160
2016-03-01 09:04:00     14095     14165
2016-03-01 09:05:00     14120     14190
2016-03-01 09:06:00     14115     14180
2016-03-01 09:07:00     14110     14170
2016-03-01 09:08:00     14110     14175
2016-03-01 09:09:00     14105     14170
2016-03-01 09:10:00     14105     14170
2016-03-01 09:11:00     14120     14180
2016-03-01 09:12:00     14105     14170
2016-03-01 09:13:00     14105     14170
2016-03-01 09:14:00     14110     14175
2016-03-01 09:15:00     14105     14175
2016-03-01 09:16:00     14120     14185
2016-03-01 09:17:00     14125     14190
2016-03-01 09:18:00     14115     14185
2016-03-01 09:19:00     14135     14195
2016-03-01 09:20:00     14125     14190
2016-03-01 09:21:00     14135     14205
2016-03-01 09:22:00     14140     14210
2016-03-01 09:23:00     14140     14200
2016-03-01 09:24:00     14135     14205
2016-03-01 09:25:00     14140     14205
2016-03-01 09:26:00     14135     14205
2016-03-01 09:27:00     14130     14205

我们以zn1.Close列的价格为X，zn2.Close列的价格为Y，那么试试找到自变量X和因变量Y的关系的表达式。

为了直观起见，我们可以先画出一张散点图，以X为横坐标，Y为纵坐标，每个点对应一个X和一个Y。


# 数据集已存在df变量中
> head(df)
                    zn1.Close zn2.Close
2016-03-01 09:01:00     14075     14145
2016-03-01 09:02:00     14095     14160
2016-03-01 09:03:00     14095     14160
2016-03-01 09:04:00     14095     14165
2016-03-01 09:05:00     14120     14190
2016-03-01 09:06:00     14115     14180

# 分别给x,y赋值
> x<-as.numeric(df[,1])
> y<-as.numeric(df[,2])

# 画图
> plot(y~x+1)

从散点图上发现 X和Y 的排列基本是在一条直线附近，那么我们可以假设X和Y的关系是线性，可以用公式表式为。

Y = a + b * X + c

Y，为因变量
X，为自变量
a，为截距
b，为自变量系数
a+b*X, 表示Y随X的变化而线性变化的部分
c, 为残差或随机误差，是其他一切不确定因素影响的总和，其值不可观测。假定c是符合均值为0方差为σ^2的正态分布，记作c~N(0,σ^2)

对于上面的公式，称函数f(X) = a + b * X 为一元线性回归函数，a为回归常数，b为回归系数，统称回归参数。X 为回归自变量或回归因子，Y 为回归因变量或响应变量。如果(X1,Y1)，(X2,Y2)…(Xn,Yn)是(X,Y)的一组观测值，则一元线性回归模型可表示为


Yi = a + b * X + ci，     i= 1,2,...n

其中E(ci)=0, var(ci)=σ^2, i=1,2,...n

通过对一元线性回归模型的数学定义，接下来让我们利用数据集做回归模型的参数估计。

3. 回归参数估计

对于上面的公式，回归参数a,b是我们不知道的，我们需要用参数估计的方法来计算出a,b的值，而从得到数据集的X和Y的定量关系。我们的目标是要计算出一条直线，使直接线上每个点的Y值和实际数据的Y值之差的平方和最小，即（Y1实际-Y1预测）^2+（Y2实际-Y2预测）^2+ …… +（Yn实际-Yn预测）^2 的值最小。参数估计时，我们只考虑Y随X的线性变化的部分，而残差c是不可观测的，参数估计法并不需要考虑残差，对于残差的分析在后文中介绍。

令公式变形为a和b的函数Q(a,b), 即 (Y实际-Y测试)的平方和，变成到(Y实际 – (a+b*X))的平方和。

公式一回归参数变形公式

通过最小二乘估计推导出a和b的求解公式，详细的推导过程请参考文章一元线性回归的细节

reg3

公式二回归参数计算公式

其中 x和y的均值，计算方法如下

reg4

公式三均值计算公式

有了这个公式，我们就可以求出a和b两个的回归参数的解了。

接下来，我们用R语言来实现对上面数据的回归模型的参数估计，R语言中可以用lm()函数来实现一元线性回归的建模过程。


# 建立线性回归模型
> lm.ab<-lm(y ~ 1+x)

# 打印参数估计的结果
> lm.ab

Call:
lm(formula = y ~ 1 + x)

Coefficients:
(Intercept)            x  
   -349.493        1.029

如果你想动手来计算也可以自己实现公式。


# x均值
> Xm<-mean(x);Xm 
[1] 14034.82

# y均值
> Ym<-mean(y);Ym
[1] 14096.76

# 计算回归系数
> b <- sum((x-Xm)*(y-Ym)) / sum((x-Xm)^2) ;b
[1] 1.029315

# 计算回归常数
> a <- Ym - b * Xm;a
[1] -349.493

回归参数a和b的计算结果，与lm()函数的计算结果是相同的。有了a和b的值，我们就可以画出这条近似的直接线。

计算公式为：

Y= a + b * X = -349.493 + 1.029315 * X

画出回归线。


> plot(y~x+1)
> abline(lm.ab)

这条直线是我们用数据拟合出来的，是一个近似的值。我们看到有些点在线上，有些点不在线上。那么要评价这条回归线拟合的好坏，我们就需要对回归模型进行显著性检验。

4. 回归方程的显著性检验

从回归参数的公式二可知，在计算过程中并不一定要知道Y和X是否有线性相关的关系。如果不存相关关系，那么回归方程就没有任何意义了，如果Y和X是有相关关系的，即Y会随着X的变化而线性变化，这个时候一元线性回归方程才有意义。所以，我们需要用假设检验的方法，来验证相关性的有效性。

通常会采用三种显著性检验的方法。

T检验法：T检验是检验模型某个自变量Xi对于Y的显著性，通常用P-value判断显著性，小于0.01更小时说明这个自变量Xi与Y相关关系显著。
F检验法：F检验用于对所有的自变量X在整体上看对于Y的线性显著性，也是用P-value判断显著性，小于0.01更小时说明整体上自变量与Y相关关系显著。
R^2(R平方)相关系统检验法：用来判断回归方程的拟合程度，R^2的取值在0，1之间，越接近1说明拟合程度越好。

在R语言中，上面列出的三种检验的方法都已被实现，我们只需要把结果解读。上文中，我们已经通过lm()函数构建一元线性回归模型，然后可以summary()函数来提取模型的计算结果。


> summary(lm.ab)      # 计算结果

Call:
lm(formula = y ~ 1 + x)

Residuals:
     Min       1Q   Median       3Q      Max 
-11.9385  -2.2317  -0.1797   3.3546  10.2766 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -3.495e+02  7.173e+01  -4.872 2.09e-06 ***
x            1.029e+00  5.111e-03 201.390  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.232 on 223 degrees of freedom
Multiple R-squared:  0.9945,	Adjusted R-squared:  0.9945 
F-statistic: 4.056e+04 on 1 and 223 DF,  p-value: < 2.2e-16

模型解读：

Call，列出了回归模型的公式。
Residuals，列出了残差的最小值点，1/4分位点，中位数点，3/4分位点，最大值点。
Coefficients，表示参数估计的计算结果。
Estimate，为参数估计列。Intercept行表示常数参数a的估计值，x行表示自变量x的参数b的估计值。
Std. Error，为参数的标准差，sd(a), sd(b)
t value，为t值，为T检验的值
Pr(>|t|) ，表示P-value值，用于T检验判定，匹配显著性标记
显著性标记，***为非常显著，**为高度显著, **为显著，·为不太显著，没有记号为不显著。
Residual standard error，表示残差的标准差，自由度为n-2。
Multiple R-squared，为相关系数R^2的检验，越接近1则越显著。
Adjusted R-squared，为相关系数的修正系数，解决多元回归自变量越多，判定系数R^2越大的问题。
F-statistic，表示F统计量，自由度为(1,n-2)，p-value:用于F检验判定，匹配显著性标记。

通过查看模型的结果数据，我们可以发现通过T检验的截距和自变量x都是非常显著，通过F检验判断出整个模型的自变量是非常显著，同时R^2的相关系数检验可以判断自变量和因变量是高度相关的。

最后，我们通过的回归参数的检验与回归方程的检验，得到最后一元线性回归方程为：

Y = -349.493 + 1.029315 * X

5. 残差分析和异常点检测

在得到的回归模型进行显著性检验后，还要在做残差分析(预测值和实际值之间的差)，检验模型的正确性，残差必须服从正态分布N(0,σ^2)。

我们可以自己计算数据残差，并进行正态分布检验。


# 残差
> y.res<-residuals(lm.ab)

# 打印前6条数据
> head(y.res)
        1         2         3         4         5         6 
6.8888680 1.3025744 1.3025744 6.3025744 5.5697074 0.7162808 

# 正态分布检验
> shapiro.test(y.res)

	Shapiro-Wilk normality test

data:  y.res
W = 0.98987, p-value = 0.1164

# 画出残差散点图
> plot(y.res)

对残差进行Shapiro-Wilk正态分布检验，W接近1，p-value>0.05，证明数据集符合正态分布！关于正态分布的介绍，请参考文章常用连续型分布介绍及R语言实现。

同时，我们也可以用R语言的工具生成4种用于模型诊断的图形，简化自己写代码计算的操作。


# 画图，回车展示下一张
> plot(lm.ab)    
Hit  to see next plot:   # 残差拟合图
Hit  to see next plot:   # 残差QQ图
Hit  to see next plot:   # 标准化的残差对拟合值 
Hit  to see next plot:   # 标准化残差对杠杆值

图1，残差和拟合值对比图

对残差和拟合值作图，横坐标是拟合值，纵坐标是残差。残差和拟合值之间，数据点均匀分布在y=0两侧，呈现出随机的分布，红色线呈现出一条平稳的曲线并没有明显的形状特征，说明残差数据表现非常好。

图2，残差QQ图

残差QQ图，用来描述残差是否符合正态分布。图中的数据点按对角直线排列，趋于一条直线，并被对角直接穿过，直观上符合正态分布。对于近似服从正态分布的标准化残差，应该有 95% 的样本点落在 [-2,2] 区间内。

图3，标准化残差平方根和拟合值对比图

对标准化残差平方根和拟合值作图，横坐标是拟合值，纵坐标是标准化后的残差平方根。与残差和拟合值对比图(图1)的判断方法类似，数据随机分布，红色线呈现出一条平稳的曲线，无明显的形状特征。

图4，标准残差和杠杆值对比图

对标准化残差和杠杆值作图，虚线表示的cooks距离等高线，通常用Cook距离度量的回归影响点。本图中没有出现红色的等高线，则说明数据中没有特别影响回归结果的异常点。

如果想把把4张图画在一起进行展示，可以改变画布布局。


> par(mfrow=c(2,2))
> plot(lm.ab)

看到上面4幅中，每幅图上都有一些点被特别的标记出来了，这些点是可能存在的异常值点，如果要对模型进行优化，我们可以从这些来入手。但终于本次残差分析的结果已经很好了，所以对于异常点的优化，可能并不能明显的提升模型的效果。

从图中发现，索引编号为27和192的2个点在多幅图中出现。我们假设这2个点为异常点，从数据中去掉这2个点，再进行显著性检验和残差分析。


# 查看27和192
> df[c(27,192),]
                    zn1.Close zn2.Close
2016-03-01 09:27:00     14130     14205
2016-03-01 14:27:00     14035     14085

# 新建数据集，去掉27和192
> df2<-df[-c(27,192),]

回归建模和显著性检验。


> x2<-as.numeric(df2[,1])
> y2<-as.numeric(df2[,2])
> lm.ab2<-lm(y2 ~ 1+x2)
> summary(lm.ab2)

Call:
lm(formula = y2 ~ 1 + x2)

Residuals:
    Min      1Q  Median      3Q     Max 
-9.0356 -2.1542 -0.2727  3.3336  9.5879 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept) -3.293e+02  7.024e+01  -4.688 4.83e-06 ***
x2           1.028e+00  5.004e-03 205.391  < 2e-16 ***
---
Signif. codes:  
0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.117 on 221 degrees of freedom
Multiple R-squared:  0.9948,	Adjusted R-squared:  0.9948 
F-statistic: 4.219e+04 on 1 and 221 DF,  p-value: < 2.2e-16

对比这次的显著性检验结果和之前结果，T检验，F检验和 R^2检验，并没有明显的效果提升，结果和我预想的是一样的。所以，通过残差分析和异常点分析，我认为模型是有效的。

6. 模型预测

最后，我们获得了一元线性回归方程的公式，就可以对数据进行预测了。比如，对给定X=x0时，计算出y0=a+b*x0的值，并计算出置信度为1-α的预测区间。

当X=x0,Y=y0时，置信度为1-α的预测区间为

reg5

即

reg6

我们可以用R语言的predict()函数来计算预测值y0，和相应的预测区间。程序算法如下。


> new<-data.frame(x=14040)
> lm.pred<-predict(lm.sol,new,interval="prediction",level=0.95)

# 预测结果
> lm.pred
       fit      lwr      upr
1 14102.09 14093.73 14110.44

当x0=14040时，在预测区间为0.95的概率时，y0的值为 14102，预测区间为[14093.73,14110.44]。

我们通过图形来表示。


> plot(y~x+1)
> abline(lm.ab,col='red')
> points(rep(newX$x,3),y=lm.pred,pch=19,col=c('red','blue','green'))

其中，红色点为y0的值，蓝色点为预测区间最小值，绿色点为预测区间最大值。

对于统计模型中最核心部分就在结果解读，本文介绍了一元回归模型的基本的建模过程和模型的详细解读方法。在我们掌握了这种方法以后，就可以更容易地理解和学习多元回归，非线性回归等更多的模型，并把这些模型应用到实际的工作中了。下一篇文章R语言解读多元线性回归模型，请继续阅读。

转载请注明出处：
http://blog.fens.me/r-linear-regression/

打赏作者

排行榜

Blog Archives

Posted:

Tags:

Comments:

AI-900认证考试攻略

1. 考试契机

2. 学习路径

3. 复习准备

Posted:

Tags:

Comments:

R语言轻巧的时间包hms

1. hms包介绍

2. hms包的使用

Posted:

Tags:

Comments:

R语言解读自回归模型

1. 自回归模型(AR)

2. 用R语言构建自回归模型

3. 模型识别ACF/PACF

4. 模型预测

Posted:

Tags:

Comments:

R语言解读多元线性回归模型

1. 多元线性回归介绍

2. 多元线性回归建模

3. 模型优化

4. 案例：黑色系期货日K线数据验证

Posted:

Tags:

Comments:

R语言解读一元线性回归模型

1. 一元线性回归介绍

2. 数据集和数学模型

3. 回归参数估计

4. 回归方程的显著性检验

5. 残差分析和异常点检测

6. 模型预测

站内导航

最新文章

最新评论

最热文章