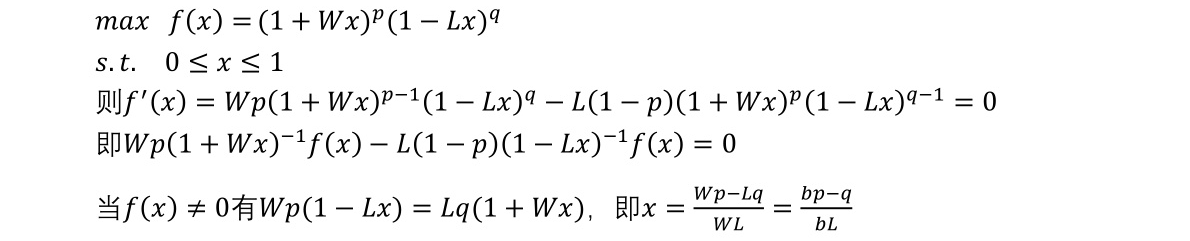用IT技术玩金融系列文章,将介绍如何使用IT技术,处理金融大数据。在互联网混迹多年,已经熟练掌握一些IT技术。单纯地在互联网做开发,总觉得使劲的方式不对。要想靠技术养活自己,就要把技术变现。通过“跨界”可以寻找新的机会,创造技术的壁垒。
金融是离钱最近的市场,也是变现的好渠道!今天就开始踏上“用IT技术玩金融”之旅!
关于作者:
- 张丹(Conan), 程序员R,Nodejs,Java
- weibo:@Conan_Z
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/finance-kelly
前言
职业做投机交易的人,应该都听说过凯利公式,这是一个通过计算胜率和赔率,来选择最佳投注比例的公式,目的是长期获得最高的盈利。
只要找到长期看必胜的局,接下来就是让时间帮我们赚钱了。
目录
- 开始赌局
- 凯利公式
- 赌局的最优解
- 让时间帮我们赚钱
1. 开始赌局
设游戏赌局,你赢的概率是80%,输的概率是20%,赢时的净收益率是100%,输时的亏损率也是100%。如果赢,你每赌1元可以赢得1元;如果输,则每赌1元将会输掉1元。赌局可以进行无限次,每次下的赌注可由你自己任意定。如果你的初始资金是100元,那么怎么样下注,才能使得长期收益最大?
对于胜率80%,从感觉上应该是很有把握的事情了。那么我们先主观判断一次,用90%的仓位去赌一下,看看结果怎么呢?如果下注10次,按80%胜率,8次胜,2次负。我们来算一下最后的结果。
# 设置胜负,1胜,0负
> win<-c(1,1,1,0,1,1,0,1,1,1)
# 分别按投注计算每回合的剩余资金
> a1<-(1+0.9)*100
> a2<-a1*(1+0.9)
> a3<-a2*(1+0.9)
> a4<-a3*0.1
> a5<-a4*(1+0.9)
> a6<-a5*(1+0.9)
> a7<-a6*0.1
> a8<-a7*(1+0.9)
> a9<-a8*(1+0.9)
> a10<-a9*(1+0.9)
> dat<-c(a1,a2,a3,a4,a5,a6,a7,a8,a9,a10)
> df<-data.frame(win,dat)
# 打印剩余资金列表
> df
win dat
1 1 190.0000
2 1 361.0000
3 1 685.9000
4 0 68.5900
5 1 130.3210
6 1 247.6099
7 0 24.7610
8 1 47.0459
9 1 89.3872
10 1 169.8356
10次交易后,赢了8次,只输了2次,我们从100元本金,上升到了169元,收益率为69%,还是不错的。最高的时候,资金为685元,收益率为685%,赚了6倍多。最低则是只剩下24元,真是赔的好惨啊!
接下来,画出资金曲线。这是一个过山车式的曲线,赚钱的时候非常猛,一旦赌输了,就产生了巨大的亏损。
# 画出资金曲线
> plot(df$dat,type='l')
曲线很陡峭,波动很大,回撤也很大,完全就是在赌博。
怎么样才能让资金曲线好看一些呢?如果每次下注用少一点资金,是不是会更好呢?那么我继续试一下。分别计算每次下注资金为 60%,40%,20%,10%的4个维度的仓位的情况。
> library(magrittr)
# 定义现金流量函数:win=胜负结果,b=赔率,pos=仓位
> postion<-function(win,b=1,pos=0.6){ # 省略代码
+ }
# 设置胜负,1胜,0负
> win<-c(1,1,1,0,1,1,0,1,1,1)
> prob<-0.8 # 胜率
> n<-10 # 赌局数
> b<-1 # 赔率
> caption<-100 # 金额
# 分别计算不同仓位的剩余现金
> pos90<-postion(win,b,0.9)*caption
> pos60<-postion(win,b,0.6)*caption
> pos40<-postion(win,b,0.4)*caption
> pos20<-postion(win,b,0.2)*caption
> pos10<-postion(win,b,0.1)*caption
# 合并到数据框
> df1<-data.frame(win,pos90,pos60,pos40,pos20,pos10)
# 打印计算结果
> df1
win pos90 pos60 pos40 pos20 pos10
1 1 190.0000 160.000 140.000 120.000 110.000
2 1 361.0000 256.000 196.000 144.000 121.000
3 1 685.9000 409.600 274.400 172.800 133.100
4 0 68.5900 163.840 164.640 138.240 119.790
5 1 130.3210 262.144 230.496 165.888 131.769
6 1 247.6099 419.430 322.694 199.066 144.946
7 0 24.7610 167.772 193.617 159.252 130.451
8 1 47.0459 268.435 271.063 191.103 143.496
9 1 89.3872 429.497 379.489 229.324 157.846
10 1 169.8356 687.195 531.284 275.188 173.631
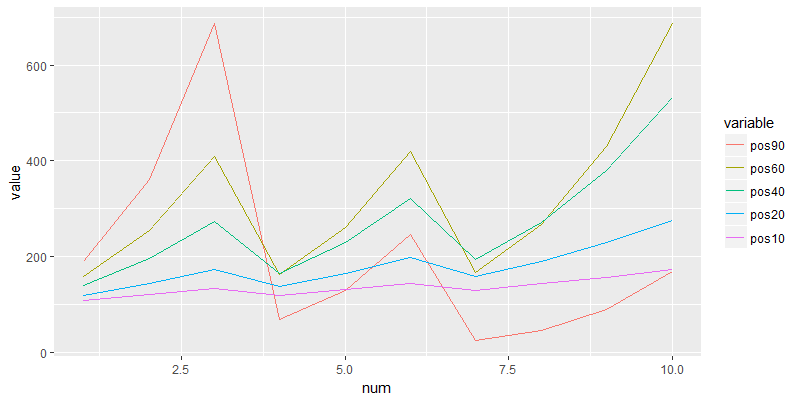
我们看到,只是简单地调整了交易的仓位比例,那么交易10次后,你剩余的现是就是有很大的不同的。其中pos60列,即60%仓位的交易,获得的回报最高为687元,而90%的仓位获得的回报,是这里面最少的。而且非常有意思的是,后面的4种仓位设置,每次交易后的资金都大于100元的原始本金。
画出资金曲线
> library(ggplot2)
> library(scales)
> library(reshape2)
# 数据转型
> df1$num<-1:nrow(df1)
> df<-melt(df1[,-1],id.vars="num")
# 画图
> g<-ggplot(df,aes(x=num,y=value,colour=variable ))
> g<-g+geom_line()
> g
从图中可以看到,对于高胜率的情况,大的仓位是可以有高回报的,但是风险也大;小仓位是相对平稳的增长。
2. 凯利公式
那么多少的仓位是最优的呢?接下来的问题,就是凯利公式会告诉我们的。
在概率论中,凯利公式(The Kelly Criterion)是一个用以使特定赌局中,拥有正期望值之重复行为长期增长率最大化的公式,由约翰·拉里·凯利于1956年在《贝尔系统技术期刊》中发表,可用以计算出每次游戏中应投注的资金比例。
除可将长期增长率最大化外,此公式不会在任何赌局中,有失去全部现有资金的可能,因此有不存在破产疑虑的优点。公式中,假设货币与赌局可无限分割,只要资金足够多,长期一定是会赚到钱的。
凯利公式的最一般性陈述为,寻找能最大化结果对数期望值的资本比例f,即可获得长期增长率的最大化。对于只有两种结果的简单赌局而言,即 输失去所有本金,胜获得资金乘以特定的赔率。
可以用下面公式来表示:
其中
- f* 投注的比例
- b 赔率,盈亏比,即平均一次盈利与一次亏损两者的比例
- p 胜率
- q 败率,即 1 – p
用凯利公式对上面的例子进行测试,胜率p=0.8,失败率q=1-p=0.2,赔率b=1,失败则下注资金完全损失,计算下注比例为
f* = (b*p-q)/b = (1*0.8-0.2)/1=0.6
所以,赌客应在每次机会中下注现有资金的60%,可以获得最大化资金的长期增长率。
通过数学变型,可以很容易得到凯利公式的另一种表达式
Kelly % = W – [(1 – W) / R]
其中Kelly % 就是上式中的f*,W就是p胜率,R就是b赔率。两者看似不同,其实完全等效一致。
对于上面的例子,我们可以计算
Kelly % = W – [(1 – W) / R] = 0.8-[(1-0.8)/1] = 0.6
凯利公式,有一个优化的变型。如果每次下注失败后,不是全部亏损,只是亏损部分,我们对上面公式可以做一个优化,增加亏损比例参数c,公式改写为下面格式
f* = (b*p-c*q)/c*b
其中
- f* 投注的比例
- b 赔率,盈亏比,即平均一次盈利与一次亏损两者的比例
- p 胜率
- q 败率,即 1 – p
- c 亏损比例
对于上面的例子,如果每次亏损是c=0.8,其他条件不变,那么我们应该用什么仓位进行交易呢?
f* = (b*p-q)/b = (1*0.8-0.8*0.2)/(0.8*1)=0.8
通过计算结果是0.8,我可以增大仓位。
凯利公式定义了长期获得最高的盈利的仓位确认的计算方法,我们自己也可以按照凯利公式的数学定义,进行推到一下。
假设一个赌局,每投资1,有p的概率可获得额外正收益W,有q=1-p的概率可获得额外的负收益-L,每次投资比例为x,建立收益为f(x)的目标函数,使得期望收益最大化。
转化为规划问题:
从推到可看出,标准的凯利公式只是当L=1的情况是一个应用,通过优化可增加了亏损比例参数。
3. 赌局的最优解
我们已经把公式介绍的很清楚了,那么接下来,就可以用程序实现进行实现了。
# 凯利公式,实现函数
> kelly<-function(prob,b=1,loss=1){ # 省略代码
+ }
用凯利公式计算的上文中的例子。
> prob<-0.8 # 胜率
> b<-1 # 赔率
> k<-kelly(prob,b,1);k
[1] 0.6
这时通过凯利公式,我们就能算出最最优的解其实是0.6的仓位设置,也就可以解释,上面的结果60%的仓位占比,获得的收益是最大的。
接下来,我们再比较一下不同的胜率和赔率的最优解是什么?
大胜率和大赔率时,可以重仓。当80%的胜率,2倍赔率时,仓位为70%。
> kelly(0.8,2)
[1] 0.7
通常情况下的赌局,不足50%的胜率,高赔率时,可以轻仓。当45%的胜率,2倍赔率时,仓位为17.5%。
> kelly(0.45,2)
[1] 0.175
通常情况下的赌局,不足50%的胜率,低赔率时,不要参考。当45%的胜率,1倍赔率时,不参与赌局。
> kelly(0.45,1)
[1] "Lost!!!"
[1] 0
小胜率,中等赔率时,不要参与。
> kelly(0.2,1)
[1] "Lost!!!"
[1] 0
小胜率,中等赔率时,中等损失,不要参与。
> kelly(0.2,1,0.5)
[1] "Lost!!!"
[1] 0
小胜率,中等赔率时,很小损失,可以All in。很小的损失比例,其实是变相的增大了赔率。
> kelly(0.2,1,0.1)
[1] "All In"
[1] 1
大胜率,很小赔率,很小损失,All in。
> kelly(0.8,0.1,0.1)
[1] "All In"
[1] 1
中胜率,很小赔率,很小损失,不要参与。
> kelly(0.45,0.1,0.1)
[1] "Lost!!!"
[1] 0
总结一下,投机操作的游戏规则。
| 胜率 | 赔率 | 损失率 | 仓位 | 指导建议 | 备注 |
|---|---|---|---|---|---|
| 80% | 2 | 100% | 70% | 重仓 | 大胜率、大赔率、全部损失 |
| 45% | 2 | 100% | 17.5% | 轻仓 | 中胜率、大赔率、全部损失 |
| 45% | 1 | 100% | 0 | 离场 | 中胜率、中赔率、全部损失 |
| 20% | 1 | 100% | 0 | 离场 | 小胜率、中赔率、全部损失 |
| 20% | 1 | 50% | 0 | 离场 | 小胜率、中赔率、中等损失 |
| 20% | 1 | 10% | 100% | 满仓 | 小胜率、中赔率、小损失 |
| 80% | 10% | 10% | 100% | 满仓 | 大胜率、小赔率、小损失 |
| 45% | 10% | 10% | 0 | 离场 | 中胜率、小赔率、小损失 |
这样我们就判断出,哪些投机操作值得玩,哪些不能玩,应该怎么玩。是不是很神奇!!
4. 让时间帮我们赚钱
根据凯利公式的定义,赌局可以进行无限次,那么当真的把赌局设置为很大时,会是什么情况呢?
我们把第一次的数据,进行100次的赌局,胜率为80%,赔率为1,金额100元,看一下结果。
> n<-100 # 赌局数
> prob<-0.8 # 胜率
> b<-1 # 赔率
> caption<-100 # 金额
# 基本二项分布,生成每盘的赌局正负
> set.seed(1)
> win<-rbinom(n,1,prob)
# 生成每盘的资金
> pos90<-postion(win,b,0.9)*caption # 90%仓位
> pos60<-postion(win,b,0.6)*caption # 60%仓位
> pos40<-postion(win,b,0.4)*caption # 40%仓位
> pos20<-postion(win,b,0.2)*caption # 20%仓位
> pos10<-postion(win,b,0.1)*caption # 10%仓位
# 打印数据
> df2<-data.frame(win,pos90,pos60,pos40,pos20,pos10)
> tail(df2)
win pos90 pos60 pos40 pos20 pos10
95 1 105083487 5.73375e+11 9874948167 5067085 34506.6
96 1 199658625 9.17399e+11 13824927434 6080503 37957.3
97 1 379351388 1.46784e+12 19354898407 7296603 41753.0
98 1 720767637 2.34854e+12 27096857770 8755924 45928.3
99 0 72076764 9.39417e+11 16258114662 7004739 41335.5
100 1 136945851 1.50307e+12 22761360527 8405687 45469.0
从100盘赌局后的结果来看,60%的仓位可以获得最高收益的,为1.50307e+12,比其他的仓位都要高少非常。
接下来,我们生成资金曲线图。
# 数据转型
> df2$num<-1:nrow(df2)
> df<-melt(df2[,-1],id.vars = "num")
# 画图
> g<-ggplot(df,aes(x=num,y=value,colour=variable ))
> g<-g+geom_line()
> g<-g+scale_y_log10() # y坐标轴log化
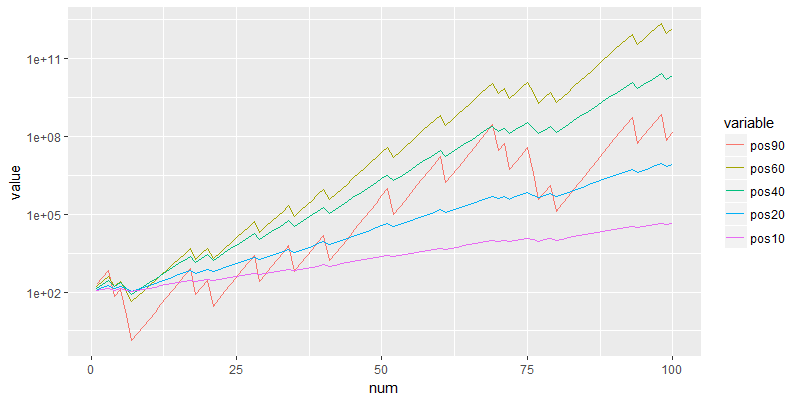
> g
资金曲线图能非常直观地告诉了我们,什么的仓位有什么样曲线形状。你如果追求低风险,就用10%仓位稳健上涨。90%接近满仓并不是最赚钱的,反而是60%的仓位是有最大的回报。
我们再用凯利公式进行计算,可以发现结果最优的结果也是60%。
> kelly(prob,1)
[1] 0.6
神奇的算法,可以有效的帮我们控制仓位,最大化长期收益。只要找到长期必胜的局,接下来就是让时间帮我们赚钱了。下一篇文章,将介绍凯利公式在金融市场应用的应用。
写文章很辛苦,如果需要获得本文源代码或加入量化投资社群,请扫下面二维码,请作者喝杯咖啡。
转载请注明出处:
http://blog.fens.me/finance-kelly