R的极客理想系列文章,涵盖了R的思想,使用,工具,创新等的一系列要点,以我个人的学习和体验去诠释R的强大。
R语言作为统计学一门语言,一直在小众领域闪耀着光芒。直到大数据的爆发,R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入,R语言的社区在迅速扩大成长。现在已不仅仅是统计领域,教育,银行,电商,互联网….都在使用R语言。
要成为有理想的极客,我们不能停留在语法上,要掌握牢固的数学,概率,统计知识,同时还要有创新精神,把R语言发挥到各个领域。让我们一起动起来吧,开始R的极客理想。
关于作者:
- 张丹,分析师/程序员/Quant: R,Java,Nodejs
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-annoy/
前言
从学习大模型到 RAG 技术,又回到了最基础的知识,如文本数据向量化,向量匹配,向量数据库等技术,因此需要继续研究基础知识。
本文就是对向量匹配算法的学习,通过近似最近邻搜索算法,可以对向量化的文字进行相似度匹配,从而进行RAG过程的高效检索。
目录
- Annoy近似最近邻搜索算法介绍
- Annoy的算法过程
- 用R语言实现Annoy算法
1. Annoy近似最近邻搜索算法介绍
Annoy全称 Approximate Nearest Neighbors Oh Yeah,是一种适合实际应用的快速相似查找算法。Annoy 是通过建立一个二叉树来使得每个点查找时间复杂度是O(log n),和kd树不同的是,Annoy没有对k维特征进行切分。
Annoy 算法的目标是建立一个数据结构能够在较短的时间内找到任何查询点的最近点,在精度允许的条件下通过牺牲准确率来换取比暴力搜索要快的多的搜索速度。
在搜索的业务场景下,基于一个现有的数据候选集(dataset),需要对新来的一个或者多个数据进行查询(query),返回在数据候选集中与该查询最相似的 Top K 数据。
最朴素的想法就是,每次来了一个新的查询数据(query),都遍历一遍数据候选集(dataset)里面的所有数据,计算出 query 与 dataset 中所有元素的相似度或者距离,然后精准地返回 Top K 相似的数据即可。
但是当数据候选集特别大的时候,遍历一遍数据候选集里面的所有元素就会耗费过多的时间,其时间复杂度是 O(n)。因此,计算机科学家们开发了各种各样的近似最近邻搜索方法(approximate nearest neighbors)来加快其搜索速度,在精确率和召回率上面就会做出一定的牺牲,但是其搜索速度相对暴力搜索有很大地提高。
在这个场景下,通常都是欧式空间里面的数据,支持的距离包括:Euclidean 距离,Manhattan 距离,Cosine 距离,Hamming 距离,Dot Product 距离
2. Annoy的算法过程
建立索引
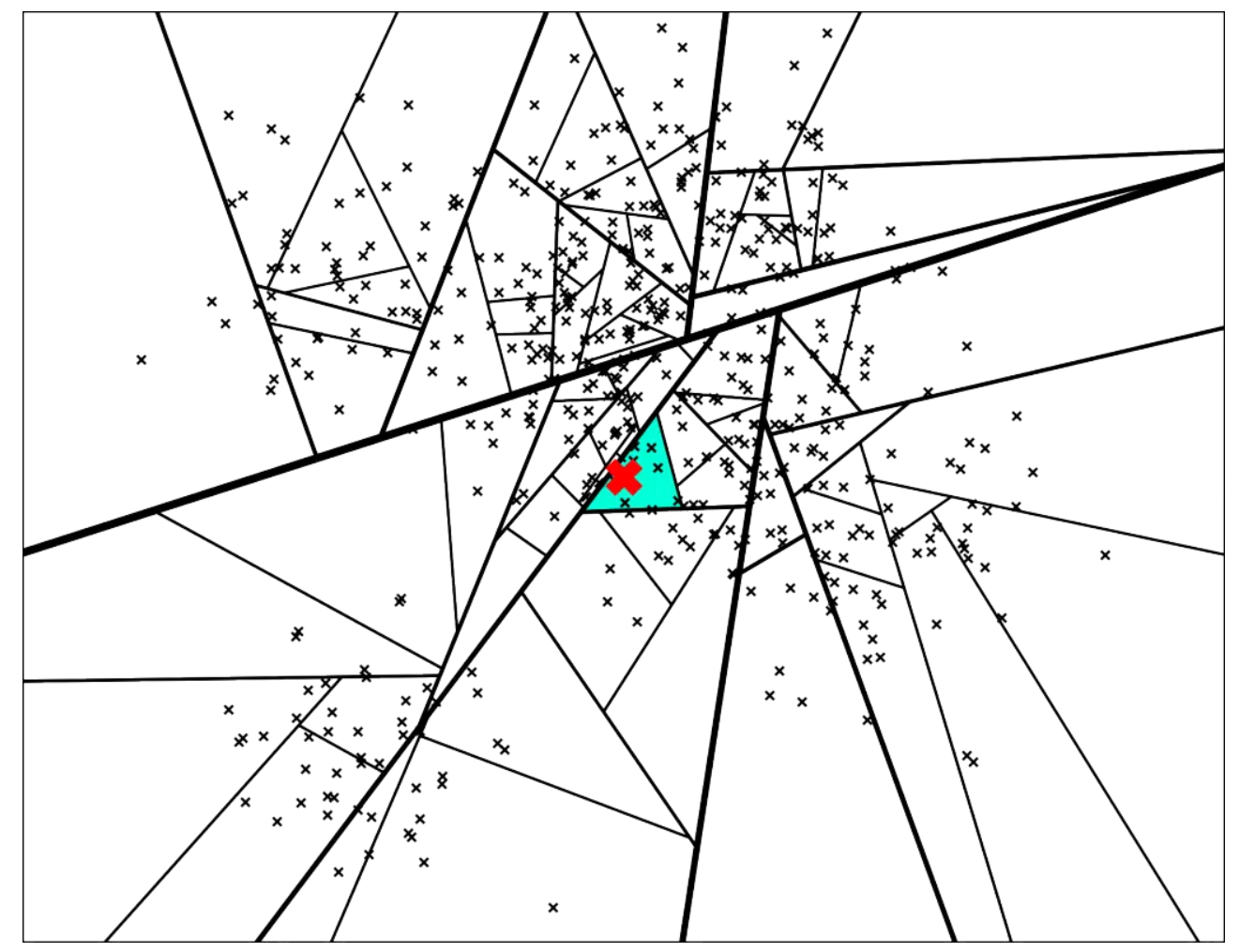
随机选择两个点,以这两个节点为初始中心节点,执行聚类数为2的kmeans过程,最终产生收敛后两个聚类中心点。这两个聚类中心点之间连一条线段(灰色短线),建立一条垂直于这条灰线,并且通过灰线中心点的线(黑色粗线)。这条黑色粗线把数据空间分成两部分。
在多维空间的话,这条黑色粗线可以看成等距垂直超平面。在划分的子空间内进行不停的递归迭代继续划分,直到每个子空间最多只剩下K个数据节点。
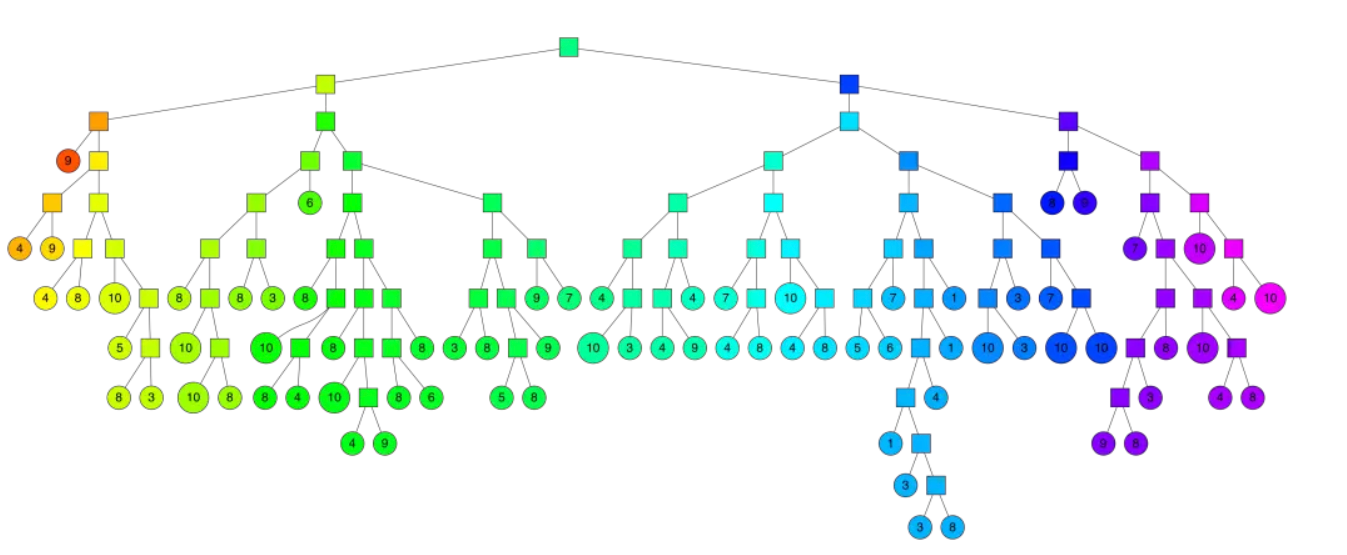
通过多次递归迭代划分的话,最终原始数据会形成二叉树结构。二叉树底层是叶子节点记录原始数据节点,其他中间节点记录的是分割超平面的信息。
Annoy建立这样的二叉树结构是希望满足这样的一个假设:相似的数据节点应该在二叉树上位置更接近,一个分割超平面不应该把相似的数据节点分在二叉树的不同分支上。
查询过程
新来的一个点(用红色的叉表示),通过对二叉树的查找,我们可以找到所在的子平面,然后里面最多有 K = 10 个点。从二叉树的叶子节点来看,该区域只有 7 个点。
二叉树底层是叶子节点记录原始数据节点,其他中间节点记录的是分割超平面的信息。Annoy建立这样的二叉树结构是希望满足这样的一个假设:相似的数据节点应该在二叉树上位置更接近,一个分割超平面不应该把相似的数据节点分在二叉树的不同分支上。查找的过程就是不断看查询数据节点在分割超平面的哪一边。
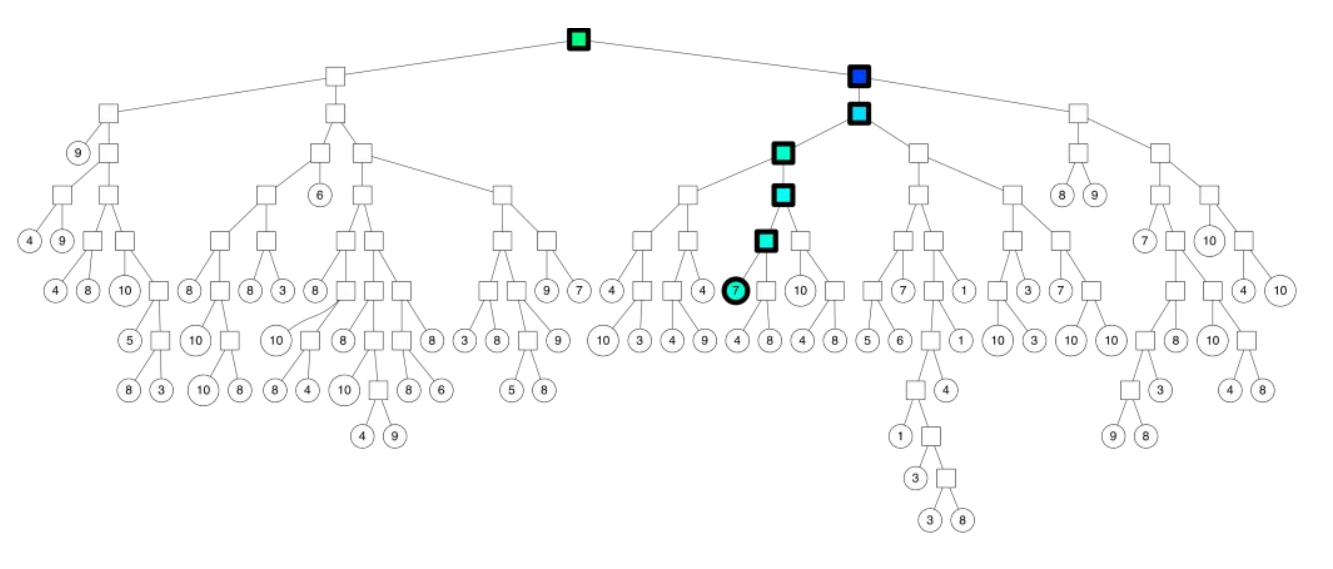
从二叉树索引结构来看,就是从根节点不停的往叶子节点遍历的过程。通过对二叉树每个中间节点(分割超平面相关信息)和查询数据节点进行相关计算来确定二叉树遍历过程是往这个中间节点左子节点走还是右子节点走。
从二叉树的根结点遍历的路径如下所示:
返回最终近邻节点
每棵树都返回一堆近邻点后,如何得到最终的Top N相似集合呢?首先所有树返回近邻点都插入到优先队列中,求并集去重, 然后计算和查询点距离, 最终根据距离值从近距离到远距离排序, 返回Top N近邻节点集合
使用优先队列(priority queue):将多棵树放入优先队列,逐一处理;并且通过阈值设定的方式,如果查询的点与二叉树中某个节点比较相似,那么就同时走两个分支,而不是只走一个分支;
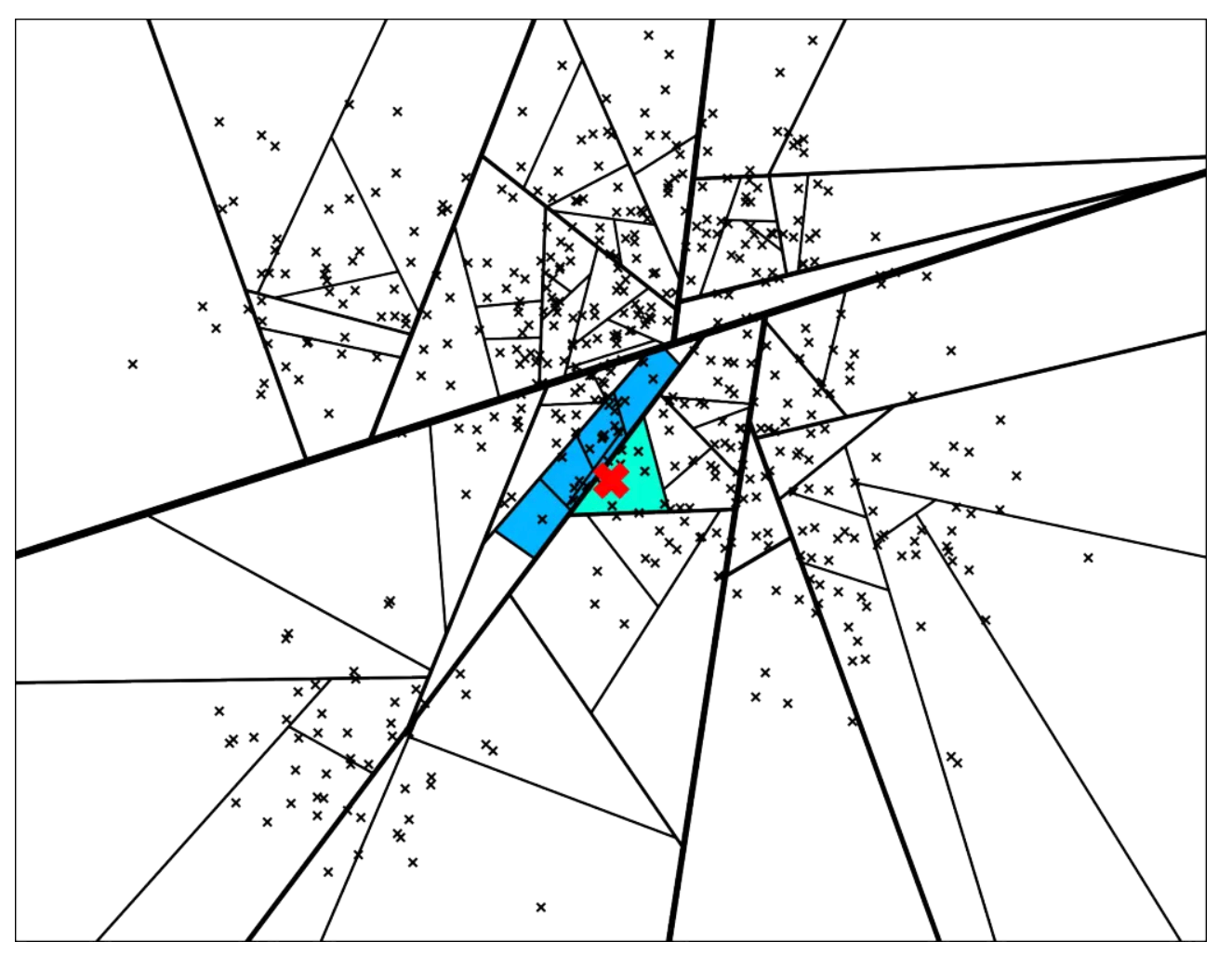
使用森林(forest of trees):构建多棵树,采用多个树同时搜索的方式,得到候选集 Top M(M > K),然后对这 M 个候选集计算其相似度或者距离,最终进行排序就可以得到近似 Top K 的结果。
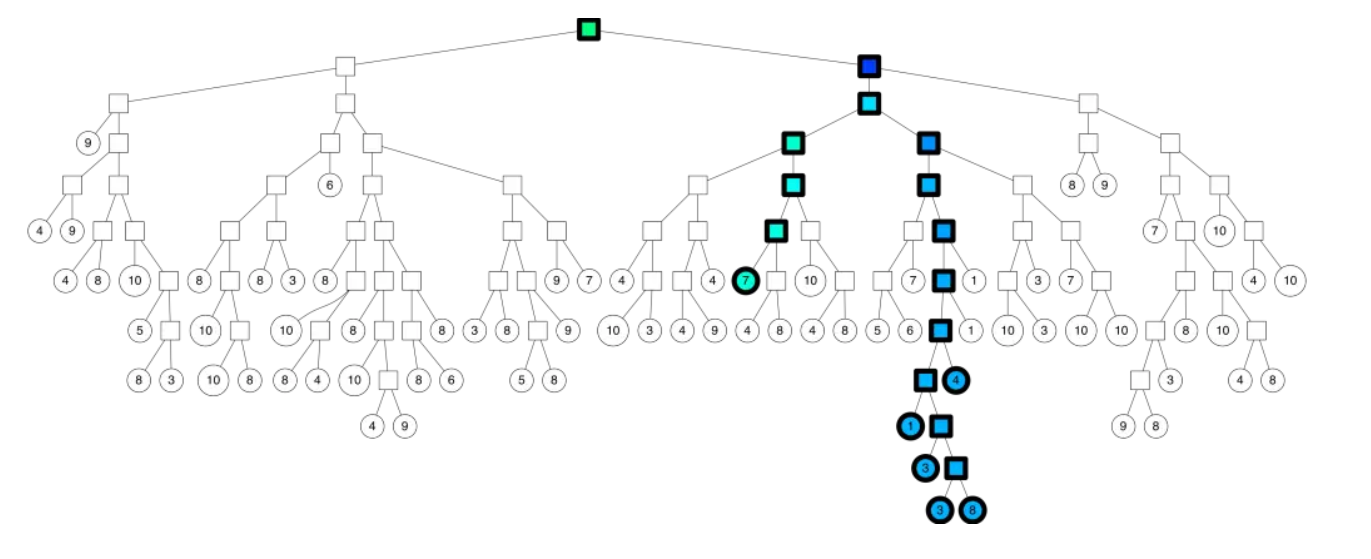
返回多棵树的相似节点,在二叉树的结构:
参考文章:https://segmentfault.com/a/1190000013713357
3. 用R语言实现Annoy算法
在R语言中,我们可以使用RcppAnnoy包,来完成Annoy算法的构建。RcppAnnoy包的地址:https://github.com/cran/RcppAnnoy
Annoy 是一个小型、快速、轻量级的近似近邻库,特别注重内存的高效使用和加载预存索引的能力。Annoy 由 Erik Bernhardsson 编写。更多特性、(Python)API 和其他语言移植请参见其页面。Annoy 隶属于 Spotify 的 “让我们为您找到您可能喜欢的其他音乐 ”算法。
3.1 RcppAnnoy包安装
首先,进行RcppAnnoy的安装和加载,整个过程比较简单。
# 安装
> install.packages("RcppAnnoy")
# 加载
> library(RcppAnnoy)
> library(magrittr) # 用于管道的工具包
3.2 生成100组向量化数据
接下来,让我们生成100组向量化数据。
# 定义每组向量数量为10
> n <- 10
# 创建基于欧式距离的annoy对象
> a <- new(AnnoyEuclidean, n)
# 设置随机种子(可以是任意数字)
> a$setSeed(42)
# 打开日志,1为打开,0为关闭
> a$setVerbose(1)
# 通过runif生成均匀分布的向量数据100组,并加入到annoy对象
> for (i in 1:100) a$addItem(i - 1, runif(n))
Reallocating to 1 nodes: old_address=(nil), new_address=0x000002ae4146ef80
Reallocating to 2 nodes: old_address=0x000002ae4146ef80, new_address=0x000002ae40818680
Reallocating to 3 nodes: old_address=0x000002ae40818680, new_address=0x000002ae3a1935f0
Reallocating to 5 nodes: old_address=0x000002ae3a1935f0, new_address=0x000002ae3dd07ab0
Reallocating to 7 nodes: old_address=0x000002ae3dd07ab0, new_address=0x000002ae416cb1d0
Reallocating to 10 nodes: old_address=0x000002ae416cb1d0, new_address=0x000002ae3dc514a0
Reallocating to 14 nodes: old_address=0x000002ae3dc514a0, new_address=0x000002ae3f9b5940
Reallocating to 19 nodes: old_address=0x000002ae3f9b5940, new_address=0x000002ae43b721b0
Reallocating to 26 nodes: old_address=0x000002ae43b721b0, new_address=0x000002ae407f2550
Reallocating to 35 nodes: old_address=0x000002ae407f2550, new_address=0x000002ae4527ce60
Reallocating to 46 nodes: old_address=0x000002ae4527ce60, new_address=0x000002ae40467470
Reallocating to 61 nodes: old_address=0x000002ae40467470, new_address=0x000002ae3bb29bf0
Reallocating to 80 nodes: old_address=0x000002ae3bb29bf0, new_address=0x000002ae405d1170
Reallocating to 105 nodes: old_address=0x000002ae405d1170, new_address=0x000002ae3b6afaa0
3.3 查看数据集
接下来,我们查看生成的数据。
# 查看有多少组数据
> a$getNItems()
[1] 100
# 取第0组向量数据,因为C++的程序索引是从0开始的,与R不同,R是从1开始的。
> a0<-a$getItemsVector(0);a0
[1] 0.001761558 0.060019139 0.931653738 0.472722173 0.843278706 0.831824481 0.768858135
[8] 0.603522480 0.558359802 0.525437832
# 取第1组向量数据
> a1<-a$getItemsVector(1);a1
[1] 0.2386040 0.6162668 0.8655570 0.7643633 0.1878769 0.3723671 0.7563977 0.0877244
[9] 0.6563932 0.7155924
# 取第2组向量数据
> a2<-a$getItemsVector(2);a2
[1] 0.85908961 0.20982422 0.27540511 0.83535612 0.28062439 0.84796673 0.61870313
[8] 0.24962090 0.62007779 0.05507875
3.4 验证计算结果
然后,我们可以计算不同组数据的相似度,使用欧式距离进行相似度判断。
# 计算第0组向量,与第0组向量的欧式距离
> a$getDistance(0, 1)
[1] 1.186404
# 手动计算,验证欧式距离的结果
> (a1-a0)^2 %>% sum %>% sqrt
[1] 1.186404
3.5 构建二叉树
完成验证后,最后我们生成二叉树的森林,生成50个。
> a$build(50)
pass 0...
Reallocating to 137 nodes: old_address=0x000002ae3b6afaa0, new_address=0x000002ae3ff11f40
pass 1...
Reallocating to 179 nodes: old_address=0x000002ae3ff11f40, new_address=0x000002ae403e0aa0
pass 2...
pass 3...
Reallocating to 234 nodes: old_address=0x000002ae403e0aa0, new_address=0x000002ae40642ee0
pass 4...
pass 5...
Reallocating to 305 nodes: old_address=0x000002ae40642ee0, new_address=0x000002ae400c8ca0
pass 6...
pass 7...
pass 8...
Reallocating to 397 nodes: old_address=0x000002ae400c8ca0, new_address=0x000002ae455f7010
pass 9...
pass 10...
pass 11...
pass 12...
Reallocating to 517 nodes: old_address=0x000002ae455f7010, new_address=0x000002ae412a7130
pass 13...
pass 14...
pass 15...
pass 16...
pass 17...
pass 18...
Reallocating to 673 nodes: old_address=0x000002ae412a7130, new_address=0x000002ae41f64010
pass 19...
pass 20...
pass 21...
pass 22...
pass 23...
pass 24...
pass 25...
Reallocating to 876 nodes: old_address=0x000002ae41f64010, new_address=0x000002ae400470e0
pass 26...
pass 27...
pass 28...
pass 29...
pass 30...
pass 31...
pass 32...
pass 33...
pass 34...
Reallocating to 1140 nodes: old_address=0x000002ae400470e0, new_address=0x000002ae414567f0
pass 35...
pass 36...
pass 37...
pass 38...
pass 39...
pass 40...
pass 41...
pass 42...
pass 43...
pass 44...
pass 45...
Reallocating to 1483 nodes: old_address=0x000002ae414567f0, new_address=0x000002ae401966c0
pass 46...
pass 47...
pass 48...
pass 49...
has 1294 nodes
这样我们就是完成了,Annoy算法索引的建立。接下来,我们使用树的能力,进行向量数据的相似度匹配。
3.6 找相近的数据
取与第0组最相近的top5的组
> a$getNNsByItem(0, 5)
[1] 0 55 54 31 11
# 同时返回距离值
> a$getNNsByItemList(0, 5, -1, TRUE)
$item
[1] 0 55 54 31 11
$distance
[1] 0.0000000 0.7477396 0.8218669 0.8747964 0.8862380
手动验证距离,分别取55,54,31,11组
# 获取数据
> a55<-a$getItemsVector(55);a55
[1] 0.4020543 0.2822408 0.7524120 0.5547701 0.7722272 0.5120775 0.6099072 0.6606834
[9] 0.6786938 0.1250148
> a54<-a$getItemsVector(54);a54
[1] 0.1175388 0.4510850 0.7032202 0.3784515 0.3057182 0.7038317 0.6994157 0.7404361
[9] 0.4291793 0.2053584
> a31<-a$getItemsVector(31);a31
[1] 0.5639953 0.3184495 0.7659245 0.6226313 0.3918578 0.8645173 0.5496733 0.8533068
[9] 0.5158110 0.6493025
> a11<-a$getItemsVector(11);a11
[1] 0.26264703 0.20268030 0.72397888 0.42269590 0.64337742 0.62916356 0.05383677
[8] 0.47857073 0.62450409 0.32770717
# 计算距离
> (a55-a0)^2 %>% sum %>% sqrt
[1] 0.7477395
> (a55-a0)^2 %>% sum %>% sqrt
[1] 0.7477395
> (a54-a0)^2 %>% sum %>% sqrt
[1] 0.8218669
> (a31-a0)^2 %>% sum %>% sqrt
[1] 0.8747964
> (a11-a0)^2 %>% sum %>% sqrt
[1] 0.886238
手动欧式距离计算结果,与a$getNNsByItem(0,5)结果一致。
3.7 减少遍历的树的数量
测试如果控制森林的数量,只遍历10棵树,而不是全部的100棵树。
> a$getNNsByItemList(0, 5, 10, TRUE)
$item
[1] 0 11 78 67 48
$distance
[1] 0.0000000 0.8862380 0.9109641 0.9520484 0.9523986
新得出的结果,就没有获得最优解,没有少了55 54 31,得出11为最接近。
3.8 生成一组新数据与原数据找相似度
生成新数据向量
# 新数据
> v <- runif(10);v
[1] 0.33498066 0.70034783 0.07155333 0.51988688 0.69538152 0.71980116 0.73188773
[8] 0.95337664 0.99446321 0.37988704
# 对比新数据找到原数据相似度最高的top5
> a$getNNsByVector(v, 5)
[1] 75 25 59 50 22
# 全量树匹配,并输出距离
> a$getNNsByVectorList(v, 5, -1, TRUE)
$item
[1] 75 25 59 50 22
$distance
[1] 0.6203443 0.7185830 0.8483184 0.8719595 0.8808730
3.9 保存模型
把模型在本地保存
# 保存模型
> a$save("./annoy01.ann")
unloaded
found 50 roots with degree 100
# 查看本地目录
> dir()
[1] "annoy.r" "annoy01.ann"
# 重新加载模型
> a$load("./annoy01.ann")
found 50 roots with degree 100
本文我们了解了近似最近邻搜索算法Annoy的原理和实现,后面就可以针对向量化的文本数据,快速地进行相似度匹配。本文代码:https://github.com/bsspirit/r-string-match/blob/main/annoy.r
转载请注明出处:
http://blog.fens.me/r-annoy/