用R模拟本次北京新冠疫情

Posted:

Jul 29, 2022

Tags:

Comments:

2 Comments

用R模拟本次北京新冠疫情

算法为王系列文章，涵盖了计算机算法，数据挖掘(机器学习)算法，统计算法，金融算法等的多种跨学科算法组合。在大数据时代的背景下，算法已经成为了金字塔顶的明星。一个好的算法可以创造一个伟大帝国，就像Google。

算法为王的时代正式到来….

关于作者：

张丹, 分析师/程序员/Quant: R,Java,Nodejs
blog: http://blog.fens.me
email: bsspirit@gmail.com

转载请注明出处：
http://blog.fens.me/r-coivd19-beijing

前言

新冠疫情已经持续三年了，前段时间在北京和上海两个超大城市爆发，一度让工作和生活陷入恐慌。当时居家办公，每天核酸，都已经变成了生活的常态。

北京疫情从4月底爆发到，到5月全面严格管控，再到6月复工复产，虽然我们都亲身经历了，但并不知道为什么北京的政策是有效的。回顾一下，让数据说话，看看我们到底我们经历了什么。

由于本人非传染病专业，文中关于传染病的专业内容大都从网上汇集和再整理，当出现本文描述与教课书不符时，请以专业教材为准。

获取北京新冠疫情数据
R0基本传染数介绍
用SIR模拟北京疫情，结果失真
用SIR拟合算出R₀，结果合理

1. 获取北京新冠疫情数据

在全球抗击新冠肺炎疫情的过程中，传染病动力学模型发挥了巨大的作用。传染病动模型，根据传染病的传播速度不同，空间范围各异，传播途径多样，动力学机理等各种因素，对传染病模型按照传染病的类型划分为 SI，SIR，SIRS，SEIR 模型。

首先，安装nCov2019，加载nCov2019包，再加载数据。关于nCov2019包的具体安装和使用，请参考文章：用R语言获取全球新冠疫情数据

# 设置工作路径
> setwd("C:/work/R/covid19")

# 如果没安装，请先安装nCov2019包
> #remotes::install_github("YuLab-SMU/nCov2019")

# 加载nCov2019包
> library(nCov2019)

# 下载最近数据
> x <- query()
Querying the latest data...
last update: 2022-07-05 
Querying the global data...
Gloabl total  555324897  cases; and  6362663  deaths
Gloabl total affect country or areas: 230
Gloabl total recovered cases: 165929
last update: 2022-07-05 
Querying the historical data...
Querying the vaccine data...
Total Candidates Programs : 51 
Querying the therapeutics data...
Total Candidates Programs : 84 
Query finish, each time you can launch query() to reflash the data

加载其他数据处理R包，并定义公共画图函数。Y轴做了log10的转化处理。

> library(ggplot2)
> library(magrittr)
> library(reshape2)
> 
> # 画图函数
> draw<-function(df){
+   dat<-melt(df,id.vars = c("date"))
+   g<-ggplot(data = dat, mapping = aes(x=date,y=value,colour=variable))
+   g<-g+geom_line() + geom_point()   
+   g<-g+scale_y_log10()
+   g<-g+ggtitle("北京疫情统计")+xlab("日期")+ylab("Log(人数)")
+   g
+ }

获取中国北京的新冠数据。

> hist<-x$historical
> beijing<-hist["China","beijing"]

# 查看数据集
> head(beijing)
    country province       date cases deaths recovered
6     China  beijing 2020-01-22    14      0         0
95    China  beijing 2020-01-23    22      0         0
184   China  beijing 2020-01-24    36      0         1
273   China  beijing 2020-01-25    41      0         2
362   China  beijing 2020-01-26    68      0         2
451   China  beijing 2020-01-27    80      1         2

计算每日新增数据，并画图展示北京整体疫情的情况。

> beijing$daily<-c(0,diff(beijing$cases))

# 画图
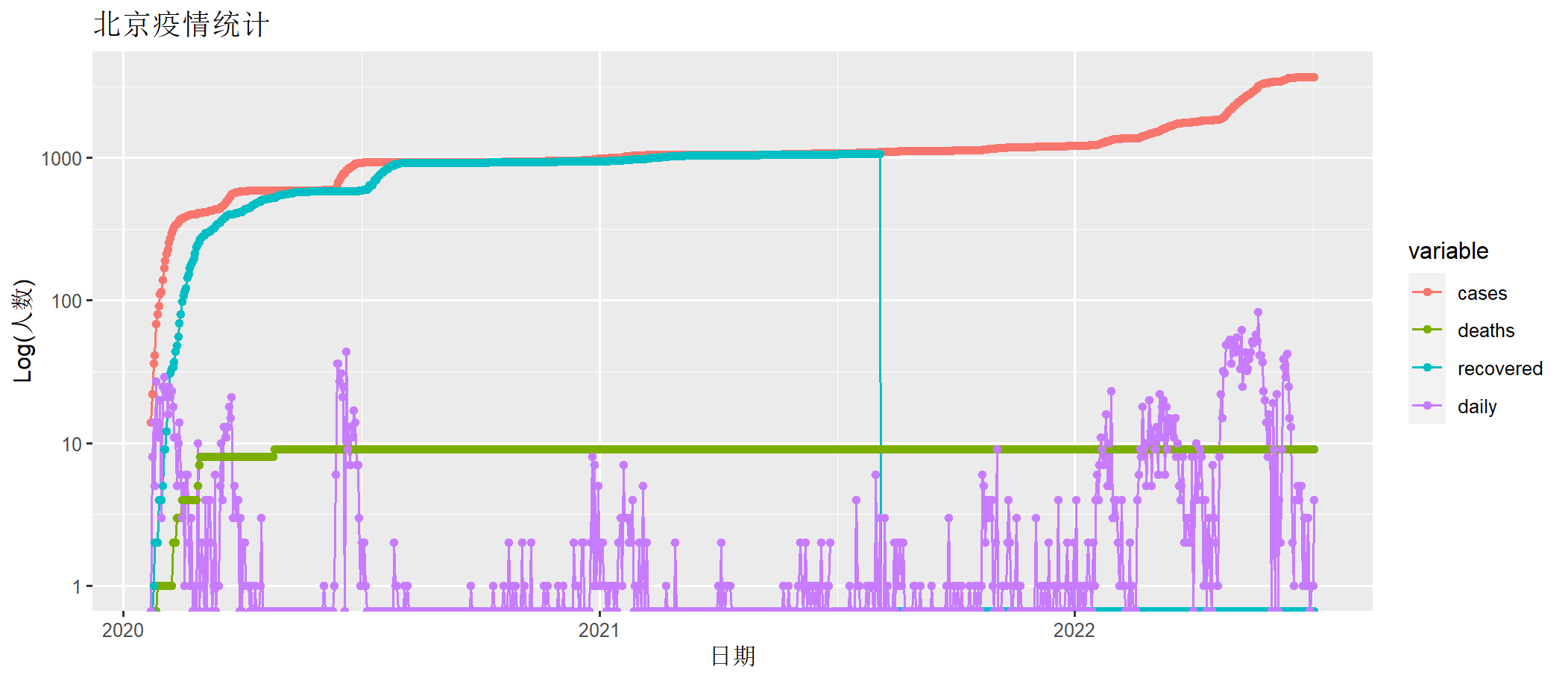
> draw(beijing[,c("date", "cases" ,"deaths", "recovered","daily")])

上图中cases为确诊人数，deaths为死亡人数，recovered为治愈人数（治愈后不会再得），daily为每日新增确诊人数。x轴为时间日期，y轴为人数（log化的人数）。

本次北京的疫情，从4月开始爆发，到6月基本控制住了。我们截取取从4月1日到7月4日数据，进行分析。

# 取2022-04-01开始到2022-07-04数据
> bj202204<-beijing[which(beijing$date>=as.Date("2022-04-01")),]
> head(bj202204)
      country province       date cases deaths recovered daily
71206   China  beijing 2022-04-01  1777      9         0     8
71295   China  beijing 2022-04-02  1777      9         0     0
71384   China  beijing 2022-04-03  1781      9         0     4
71473   China  beijing 2022-04-04  1791      9         0    10
71562   China  beijing 2022-04-05  1795      9         0     4
71651   China  beijing 2022-04-06  1800      9         0     5

# 计算这段时间的累计确诊数量
> bj202204$cum<-cumsum(bj202204$daily) 

# 画图
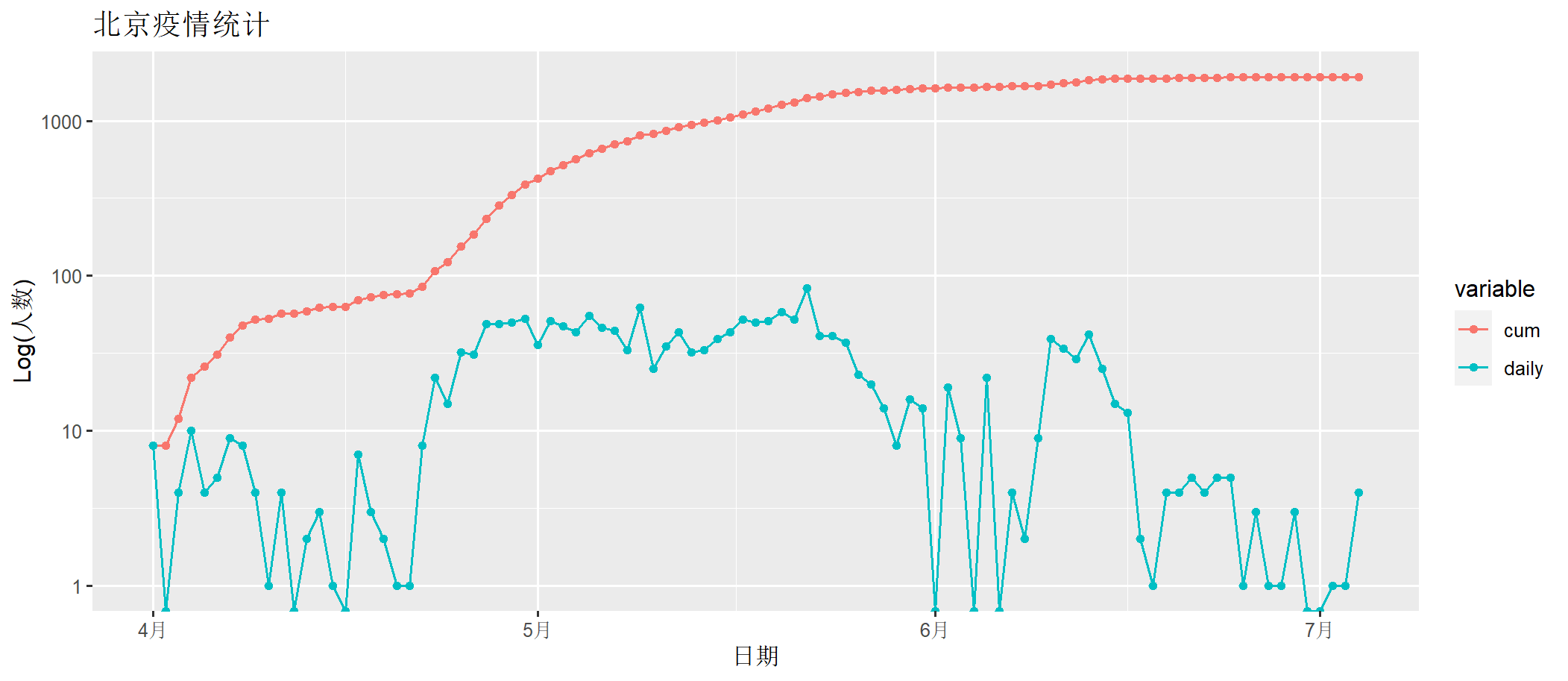
> draw(bj202204[,c("date", "cum","daily")])

上图中， daily为每日确诊数量，cum为累计确诊数量。x轴为时间日期，y轴为人数（log化的人数）。

2. R₀基本传染数和R_e有效传染数

在有了数据后，我们接下来要先了解一下R₀基本传染数的概念，后面在用传染病动力学模型做拟合时，就可以用来对实际的疫情进行评价。

2.1 R₀基本传染数

R₀基本传染数，这是一个很重要的传染病学概念，用来衡量病原体的传染性。R₀是指在一个完全易感人群中（没有任何预防手段介入并且所有人对此病原体没有免疫力的情况下），一个病例能传染的平均人数。

R₀最常用的方法是使用累积发病率数据。

R₀ = 传染期 * 每人每天的接触者数 * 每个接触者的感染概率

若R₀ < 1，意味着在没有防控的情况下，一个感染者将传给少于一个人，所以传染病将会自行逐渐消失。
若R₀ > 1，每个感染者能传染多于一个人，那么就会有发展成流行病（epidemic）的可能性。但是一般不会永远持续，因为可能被感染的人口会慢慢减少。部分人口可以死该传染病，部分则可能治愈后产生免疫力。
若R₀ = 1，传染力维持，病院持续存在，会变成地方性流行病。

但R₀不代表当前被感染的总人数。它也不是疾病严重程度的衡量指标。它只表示一个感染者平均能感染几个人，而不是告诉我们这些感染者疾病的严重程度。

对于一个特定的传染病，R₀不一定是恒定的，它可能取决于人口密度和接触方式等因素。尽管如此，对于不同人群，一个特定传染病的R₀是相对相似的。

部分传染病的R₀值，数据来源 https://zh.m.wikipedia.org/zh-cn/基本传染数

疾病	传播途径	R₀
麻疹	空气传播	12-18
白喉	唾液	6-7
天花	空气传播、飞沫传播	5-7
脊髓灰质炎	粪口传播	5-7
风疹	空气传播、飞沫传播	5-7
流行性腮腺炎	呼吸道飞沫	10-12
HIV/AIDS	性传播	4.5
百日咳	空气传播、飞沫传播	5.5
SARS	空气传播、飞沫传播、粪口传播	2-5
流行性感冒（1918年流感大流行）	空气传播、飞沫传播	2-3
埃博拉出血热（西非埃博拉病毒疫症）	体液传播	1.5-2.5
COVID-19	飞沫传播、接触传播、粪口传播	1.4-3.8 3.8–8.9（截至2020年6月） Delta变异株：5.1 Alpha变异株：4–5 Omicron变异株：7
中东呼吸综合征	呼吸道飞沫	0.5 (0.3 –0.8 )
普通感冒	呼吸道飞沫	2–3
水痘	空气传播疾病	10–12

有了上面的不同传染病的比较级，就能对本次新冠疫情有了一个数量上的感觉，Omicron变异株：7的数值，确实是非常高的传染性。

2.2 R_e有效传染数

相对于R₀，另一个指标R_e可以帮我们分析，如何抑制疫情的爆发。R_e为有效传染数，是指一个群体在任何特定的时间，不完全易感或已采取适当防控措施的情况下，单例病例能感染的平均人数。随着人口越来越多地获得免疫，无论是通过感染或接种疫苗后的个体免疫，还是随着人们的死亡，它都会发生变化。

R_e ＝ R₀ *（1 – 有效控制率）*（易感人群比例）

当R_e>1时，每个受感染的个体将疾病传播给不止一个人，疾病可能在人群中传播。
当R_e<1时，可能会发生个体病例传播给另一个人发生新的感染，要遏制疾病流行，R_e必须小于1，疫苗通过减少易感人群的比例，是使R_e < 1的最佳手段。

3. 用SIR模型模拟北京疫情

我们首先用SIR模型进行北京疫情的模拟，具体操作，使用确定的SIR公式，通过设置参数带入模型模拟本次疫情的情况，观察SIR模型模拟的数据是否与实际发生的确诊数据，是否是匹配的。

我们直接使用EpiModel包，自带的SIR模型进行拟合。关于EpiModel包的详细使用介绍，请参考文章 EpiModel快速上手传染病模型。

R程序实现代码

> library(EpiModel)
> param <- param.dcm(inf.prob = 0.5, act.rate = 0.5, rec.rate = 1/7)
> init <- init.dcm(s.num = 30*1000*1000, i.num = 8, r.num = 0)
> control <- control.dcm(type = "SIR", nsteps = 200, dt = 0.5)
> mod <- dcm(param, init, control)

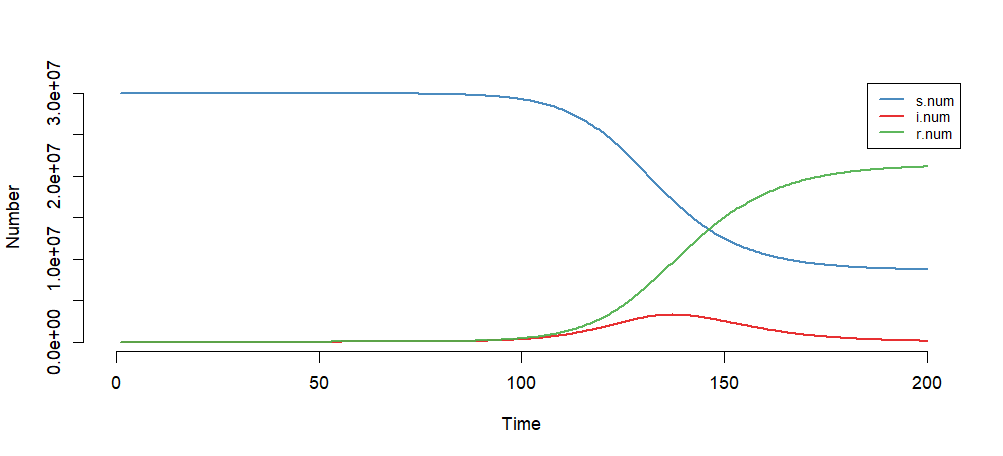
设置模型初始参数：日感染率inf.prob=0.5，日传播率 act.rate=0.5，恢复率rec.rate=1/7。易感染者s.num=30*1000*1000，为北京人口数量，已感染者i.num=0，治愈r.num=0，观察周期nsteps=200。

> mod
EpiModel Simulation
=======================
Model class: dcm

Simulation Summary
-----------------------
Model type: SIR
No. runs: 1
No. time steps: 200
No. groups: 1

Model Parameters
-----------------------
inf.prob = 0.5
act.rate = 0.5
rec.rate = 0.1428571

Model Output
-----------------------
Variables: s.num i.num r.num si.flow ir.flow num

模型模拟结果

> plot(mod)

把实际的北京确诊数据，与模拟的确认数据画到一起。


# 生成日期列
> moddf<-as.data.frame(mod)
> moddf$date<-as.Date("2022-04-01")+0:(nrow(moddf)-1)

# 合并数据集
> d1<-data.frame(date=moddf$date,i=moddf$i.num,variable="sir")
> d2<-data.frame(date=bj202204$date,i=bj202204$cum,variable="real")
> mdf<-rbind(d1,d2)

# 画图
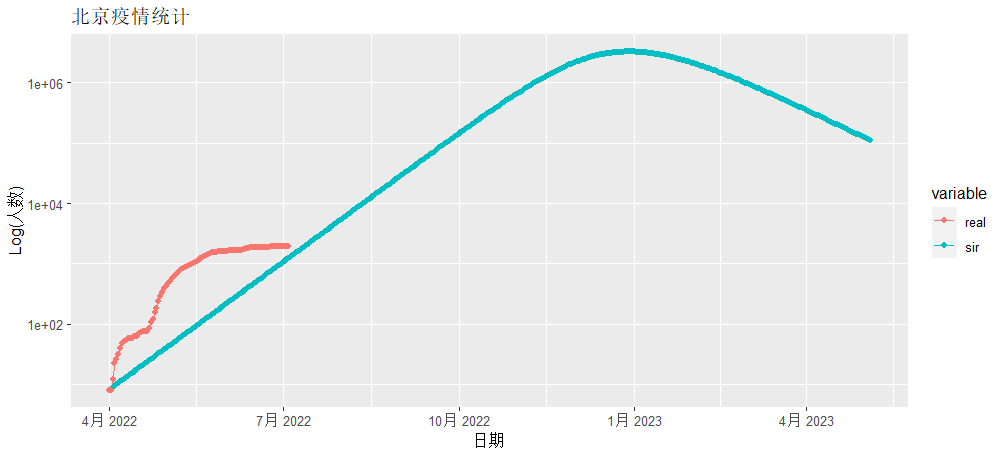
> g<-ggplot(data = mdf, mapping = aes(x=date,y=i,colour=variable))
> g<-g+geom_line() + geom_point()   
> g<-g+scale_y_log10()
> g<-g+ggtitle("北京疫情统计")+xlab("日期")+ylab("Log(人数)")
> g

红色为北京实际发生确诊的数据，蓝色线为SIR模型模拟的数据，从图中看是有很大的差异性的，所以直接用确定性的公式做疫情的模拟是很不靠谱的。

4. 基于 SIR 拟合北京疫情

使用SIR模型进行拟合，并设置运行参数


# 加载程序包
> library(lubridate)
> library(plyr)

# 设置初始化参数
> cases <- bj202204$cum     # 每日累计
> N <- 30*1000*1000         # 总人数
> startDay <- 6             # 开始累计时间

# 计算每日累计确诊
> infected <- cases[startDay:length(cases)]
> infected
 [1]   31   40   48   52   53   57   57   59   62   63   63   70   73   75   76   77   85  107  122  154
[21]  185  234  283  333  386  422  473  520  563  618  664  708  741  803  828  863  906  938  971 1010
[41] 1053 1105 1155 1206 1264 1316 1399 1440 1481 1518 1541 1561 1575 1583 1599 1613 1613 1632 1641 1641
[61] 1663 1663 1667 1669 1678 1717 1751 1780 1822 1847 1862 1875 1877 1878 1882 1886 1891 1895 1900 1905
[81] 1906 1909 1910 1911 1914 1914 1914 1915 1916 1920

# 以多少天为窗口计算R0
> window <- 12

定义SIR模型的拟合函数，用来进行后面的数据拟合。SIR模型的计算公式详解，请参考文章：用R语言解读传染病模型


# 定义SIR模型的拟合函数
> SIR<-function(time,vars,params){
+   with(as.list(c(vars,params)),{ #beta=rio,gamma=mu
+     num <- s.num + i.num + r.num
+     dS<- -beta * i.num * s.num/num
+     dI<- beta * i.num * s.num/num - gamma * i.num
+     dR<- gamma * i.num
+     return(list(c(dS,dI,dR)))
+   })
+ }

这里没有直接使用EpiModel包的SIR函数的原因是，EpiModel的参数命名规则不太一样，另外需要设置额外的参数，在这里用不上，比如inf.prob、act.rate等。当然如果一定用EpiModel的SIR函数，可以使用mod_SI_1g_cl(t, t0, parms)函数，自己做一下适配，并不复杂。


# 查看mod_SIR_1g_cl函数定义
> mod_SIR_1g_cl
function (t, t0, parms) 
{
    with(as.list(c(t0, parms)), {
        num <- s.num + i.num + r.num
        lambda <- inf.prob * act.rate * i.num/num
        if (!is.null(parms$inter.eff) && t >= inter.start) {
            lambda <- lambda * (1 - inter.eff)
        }
        si.flow <- lambda * s.num
        ir.flow <- rec.rate * i.num
        dS <- -si.flow
        dI <- si.flow - ir.flow
        dR <- ir.flow
        list(c(dS, dI, dR, si.flow, ir.flow), num = num)
    })
}

接下来，定义损失函数，由于后续采用的是最小二乘，所以都是适用与回归的损失函数。


> mse <- function(infected, fit) {
+   sum((infected - fit)^2) / length(infected)
+ }
> r2 <- function(infected, fit) {
+   1 - mse(infected, fit)/var(infected)
+ }

定义R₀的拟合函数

> R0 <- function(days){
+ 
+   # 取窗口期内的数据拟合
+   WindowInfected <- infected[(days - window):(days - 1)]
+   # 持续天数
+   Days <- 1:(length(WindowInfected))
+   
+   # 设置SIR模型的默认值，s.num易感人群，i.num已感人群，r.num已治愈人群
+   init <- c(s.num = N - WindowInfected[1], i.num = WindowInfected[1], r.num = 0)
+ 
+   # 定义损失函数
+   LOSS <- function(parameters) {
+     names(parameters) <- c("beta", "gamma")
+     out <- ode(y = init, times = Days, func = SIR, parms = parameters)
+     fit <- out[ , 3]
+     -r2(WindowInfected,fit)
+   }
+ 
+   # 拟合计算
+   Opt = optim(c(0.5, 0.5), LOSS, method = "L-BFGS-B", lower = c(0, 0), upper = c(Inf, 1))
+   Opt_par = setNames(Opt$par, c("beta", "gamma"))
+   data.frame(days = days,
+              R0 = Opt_par["beta"] / Opt_par["gamma"],
+              beta = Opt_par["beta"],
+              gamma = Opt_par["gamma"],
+              value = Opt$value,
+              date = ymd("2022-04-01") + days(startDay + days - 1) - 1) # StartDay - 1 | days - 1
+ }

从13个日期2022-04-18开始，对每一个时间进行拟合，计算R₀值。


> # 找到需要计算的日期
> days<-(window+1):(length(infected));days
 [1] 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46
[35] 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
[69] 81 82 83 84 85 86 87 88 89 90

> # 计算R0的计算
> RODF<-lapply(days,R0) %>% ldply
> head(RODF)
  days       R0      beta     gamma      value       date
1   13 1.163701 0.5813041 0.4995306 -0.5091804 2022-04-18
2   14 1.115407 0.5574453 0.4997684 -0.7966765 2022-04-19
3   15 1.081334 0.5405033 0.4998486 -0.9677076 2022-04-20
4   16 1.070063 0.5348910 0.4998687 -0.9729603 2022-04-21
5   17 1.072671 0.5362001 0.4998738 -0.9679795 2022-04-22
6   18 1.065505 0.5326116 0.4998677 -0.9529303 2022-04-23

画图输出R₀的预测值，从预测结果看，在5月初R0是最高点，是扩散最严重的时刻，北京市也是在4月底发紧急通知，封闭朝阳区的小区，并且5月份限制办公聚集，居家上班等强制干预行动，每天进行核酸检测。到6月初才放开跨区工作，逐步恢复工作秩序。

> plot(R0~date,data=RODF)

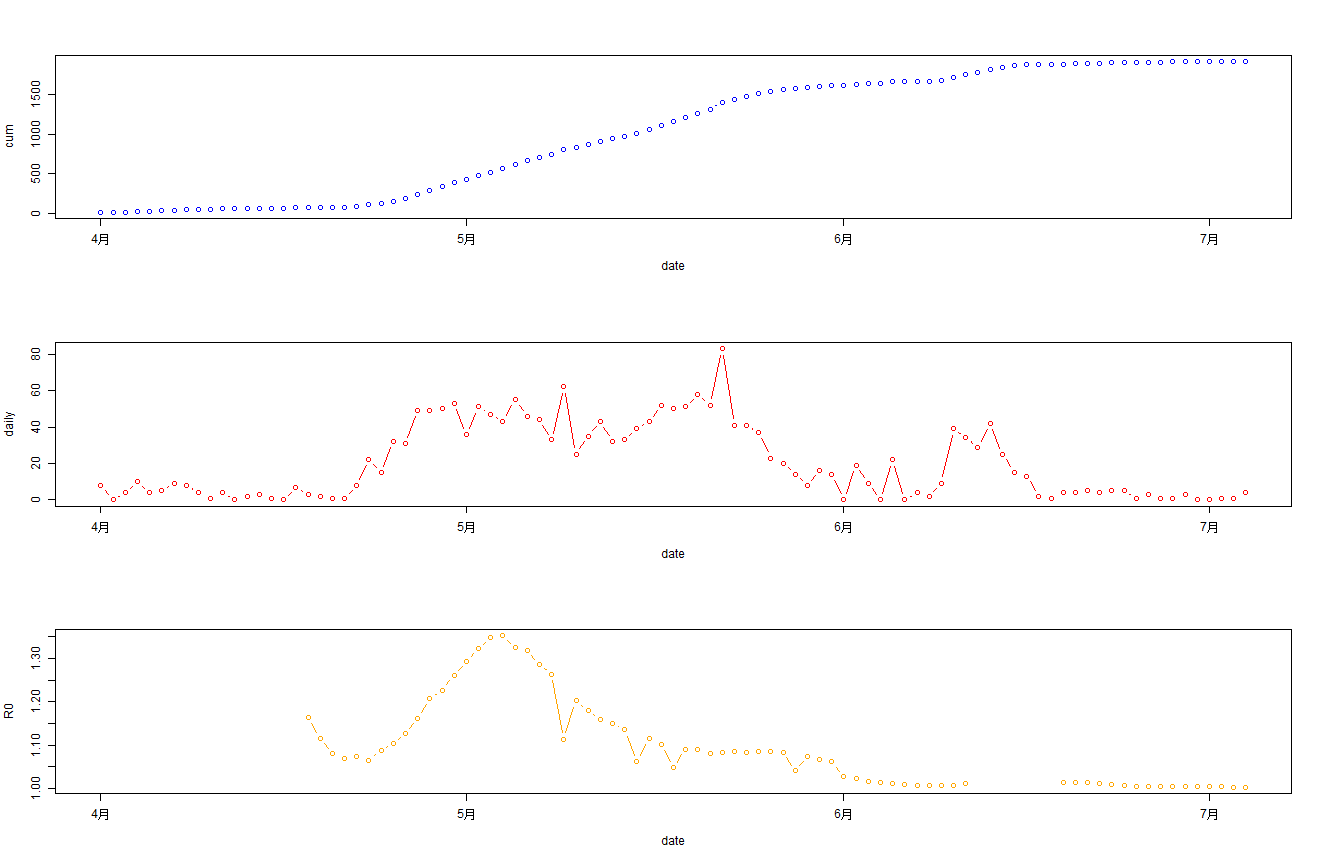
单独看一个R₀的图并不明显，我们把累计确诊，每日新增确诊和R₀值，合并在一起进行输出结果，以x轴为时间统一对齐。

> par(mfrow = c(3, 1))
> plot(cum~date,data=bj202204,type='b',col="blue")
> plot(daily~date,data=bj202204,type='b',col="red")
> 
> d2<-data.frame(date=RODF$date,R0=RODF$R0)
> d1<-data.frame(date=as.Date('2022-04-01')+0:16,R0=NA)
> d2<-rbind(d1,d2)
> plot(R0~date,data=d2,type='b',col="orange")

从2022年04月01日开始，最上面蓝色图为每日累计确诊病例，中间红色图为每日新增确诊，最下面橙色图为R₀值。

通过观察R₀值，很明显的能看到R₀值在5月初达到顶点后，R₀值开始大幅下降。从5月每日确诊人数来看趋势是平稳的，而且也在降低，因此说明北京本次防控是有效的。6月份逐步放开管制后，大家的工作和生活开始逐步恢复正常状态。

文本完整的代码，已经上传github，可以自由下载使用：https://github.com/bsspirit/infect/blob/main/code/beijing.r

转载请注明出处：
http://blog.fens.me/r-coivd19-beijing

打赏作者

Post Views: 1,009

This entry was posted in R语言实践

0 0 votes

Article Rating

This site uses Akismet to reduce spam. Learn how your comment data is processed.

2 Comments

Oldest

Newest Most Voted

Inline Feedbacks

View all comments

梁雪枫

1 year ago

拟合R0值是有问题的，R0不会因为防控发生变化，拟合的应该是Re值。

Dan Zhang

Reply to 梁雪枫

1 year ago

上面是对R0每天进行拟合的，应该能体现防控的变化吧。Re的拟合，等回头有时间我试一下。谢谢提示。

排行榜

Posted:

Tags:

Comments:

用R模拟本次北京新冠疫情

1. 获取北京新冠疫情数据

2. R₀基本传染数和R_e有效传染数

3. 用SIR模型模拟北京疫情

4. 基于 SIR 拟合北京疫情

站内导航

最新文章

最新评论

最热文章

排行榜

Posted:

Tags:

Comments:

用R模拟本次北京新冠疫情

1. 获取北京新冠疫情数据

2. R0基本传染数和Re有效传染数

3. 用SIR模型模拟北京疫情

4. 基于 SIR 拟合北京疫情

站内导航

最新文章

最新评论

最热文章

2. R₀基本传染数和R_e有效传染数