算法为王系列文章,涵盖了计算机算法,数据挖掘(机器学习)算法,统计算法,金融算法等的多种跨学科算法组合。在大数据时代的背景下,算法已经成为了金字塔顶的明星。一个好的算法可以创造一个伟大帝国,就像Google。
算法为王的时代正式到来….
关于作者:
- 张丹, 分析师/程序员/Quant: R,Java,Nodejs
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-infectious-disease
前言
传染病学是人们在不断地同危害人类健康严重的疾病作斗争中发展起来的,新冠疫情已经持续三年了,近期在北京和上海两个超大城市,还在不停的变种和传播,居家办公,每天核酸,都已经变成了生活的常态。
好奇心驱使我要研究一下传染病,为什么疫情会有这么大的传染性,如果不做防控会怎么样。结合传染病学的专业知识,通过R语言的技术手段,彻底明白了传染病传播的一些底层原理。
由于本人非传染病专业,文中关于传染病的专业内容大都从网上汇集和再整理,当出现本文描述与教课书不符时,请以专业教材为准。
目录
- 传染病动力学介绍
- 自由增长模型
- SI模型
- SIS模型
- SIR模型
1. 传染病动力学介绍
在全球抗击新冠肺炎疫情的过程中,传染病动力学模型发挥了巨大的作用。传染病动模型,根据传染病的传播速度不同,空间范围各异,传播途径多样,动力学机理等各种因素,对传染病模型按照传染病的类型划分为 SI,SIR,SIRS,SEIR 模型。
对传染病的研究方法主要有四种:描述性研究、分析性研究、实验性研究和理论性研究。传染病动力学是对传染病进行理论性定量研究的一种重要方法。它是根据种群生长的特性,疾病的发生及在种群内的传播、发展规律,以及与之有关的社会等因素,建立能反映传染病动力学特性的数学模型。通过对模型动力学性态的定性、定量分析和数值模拟,来显示疾病发展程,寻找对期预防和控制的最优策略。
2. 自由增长模型
自由增长模型,是一种条件最简单的传染病模型,模型整体上呈现指数增长趋势,对传染病传播率ρ非常敏感。模型适合于古代医疗条件不发达、不懂得对病人进行防疫隔离时,发生恶性瘟疫的情形。
模型假设:
- I(t)为t时刻的感染者人数,I(t)是连续、可微函数。
- ρ是常数,为每个病人每天有效接触的人数,即足以使人致病的接触, ρ >0
模型构建:
- 从t到t+Δt的时间里,病人增加的人数为
I(t+Δt) – x(t) = ρ * I(t)* Δt
模型求解:
- 当t=0时,初始病人人数为 I0 得,
𝑑𝐼/𝑑𝑡= ρ * I
I(0) = I0
R语言代码实现
# 加载程序包
> library(deSolve) # 用于计算积分
> library(magrittr)
> library(ggplot2)
> library(reshape2)
> setwd("C:/work/R/covid19")
定义2个公共函数,draw()函数用于画图,rbinddf()函数用于list转型为data.frame。
# 画图函数
> draw<-function(sdf,title="SIR模型",ylab="感染人数",xlab="时间周期",ylog=FALSE){
+ g<-ggplot(data = sdf, mapping = aes(x=time,y=value,colour=type))
+ g<-g+geom_line() + geom_point() #绘制线图和点图
+ g<-g+scale_shape_manual(values = c(21,23)) #自定义点形状
+ if(ylog) g<-g+scale_y_log10()
+ g<-g+ggtitle(title)+xlab(xlab)+ylab(ylab)
+ g
+ }
# 按行合并
> rbinddf<-function(ldf=list(),names=NULL){
+ n <- length(ldf)
+ res <- NULL
+ if(n>0){
+ for (i in seq(n)) {
+ if(!is.null(names)){
+ type <- names[i]
+ }
+ res <- rbind(res, data.frame(ldf[[i]],type=type))
+ }
+ }
+ return(res)
+ }
定义自由增长模型内核函数
# case1 自由增长模型
> calc1 <- function(rio = 0.3, # 传染率系数,每个病人每天传染的人数
+ times = 0:20, # 病情发展时间
+ I = 1) { # 已感染者1人
+ # 公式
+ s_equations <- function(times, vars, params) {
+ with(as.list(c(vars, params)), {
+ dI <- rio * I
+ return(list(dI))
+ })
+ }
+
+ # 解微分方程
+ ode(
+ func = s_equations,
+ y = c(I = I),
+ times = times,
+ parms = c(rio = rio)
+ ) %>% as.data.frame
+ }
分别计算当ρ(rio) = 0.3, 0.25, 0.2 时的感染者人员。
> s1 <- calc1(rio = 0.3)
> s2 <- calc1(rio = 0.25)
> s3 <- calc1(rio = 0.2)
# 合并3组结果
> sdf1<-rbinddf(list(s1,s2,s3),names=c("s1","s2","s3"))
> head(sdf1) # 查看数据集
time I type
1 0 1.000000 s1
2 1 1.349861 s1
3 2 1.822121 s1
4 3 2.459609 s1
5 4 3.320123 s1
6 5 4.481699 s1
把模拟进行可视化展示。
> names(sdf1)<-c("time","value","type")
> draw(sdf1,title="自由增长模型",ylab="感染人数",xlab="时间周期")
自由增长模型,并不符合实际情况。在病人有效接触的人群中,有健康人也有病人,而其中只有健康人才可以被传染为病人,所以我们接下来介绍的SI模型,就区别2类人群。
3. SI模型
SI模型,适用于只有易感者和患病者两类人群,且不会反复发作的疾病。人群分为易感染者(Susceptible)和已感染者(Infective)两类(取两个词的首字母,称之为SI模型)。
易感者与患病者有效接触即被感染,变为患病者,无潜伏期、无治愈情况、无免疫力。SI模型对传染病传播率ρ非常敏感,而且只要我们把每个病人、每天接触的人数有效降低,传染病的传染速度就会变得非常慢。只要防疫力度够大,控制住传染病是完全可能的。这种模型比较适合,被传染后无法恢复健康的,比如HIV等情形。
模型假设:
- I(t)为t时刻的感染者人数,I(t)是连续、可微函数。
- ρ是常数,为每个病人每天有效接触的人数,即足以使人致病的接触, ρ >0
- 在疾病传播期内所考察地区的总人数不变,不考虑生死和迁移。
- 当病人与健康者有效接触时,使健康者受感染变为病人
模型构建:
已感染人数为 N * i(t),所有已感染人每天有效接触人数为 ρ * N * i(t),其中被传染的易感染人的比例 s(t),因此每天增加的感染者人数为 ρ * N * i(t) * s(t)。
- N:总人数,不变
- s(t):t时刻易感染者在总人数中所占比例。
- i(t):t时刻已感染者在总人数中所占比例。
- ρ是常数,每个病人每天有效接触的平均人数是常数,称为日接触率, ρ >0
从t到t+Δt的时间里,病人增加的人数为
N * (i(t+Δt)– i(t)) = ρ * i(t) * s(t) * Δt
模型求解:
- N总人数不变,因此 s(t) + i(t) = 1
- 当t=0时,初始病人占比为 i0 得,
𝑑𝑖/𝑑𝑡= ρ * i * (1-i)
i(0) = 𝑖0
编写模型内核函数。
> calc2 <- function(rio = 0.3, # 接触率,传染率系数
+ times = 0:100, # 病情发展时间
+ i = 0.000001) { # 已感染者,初始占比:百万分之一
+ # 公式
+ si_equations <- function(time, vars, params) {
+ with(as.list(c(vars, params)), {
+ di <- rio * i * (1 - i)
+ return(list(di))
+ })
+ }
+
+ # 解微分方程
+ ode(
+ func = si_equations,
+ y = c(i = i),
+ times = times,
+ parms = c(rio = rio)
+ ) %>% as.data.frame
+ }
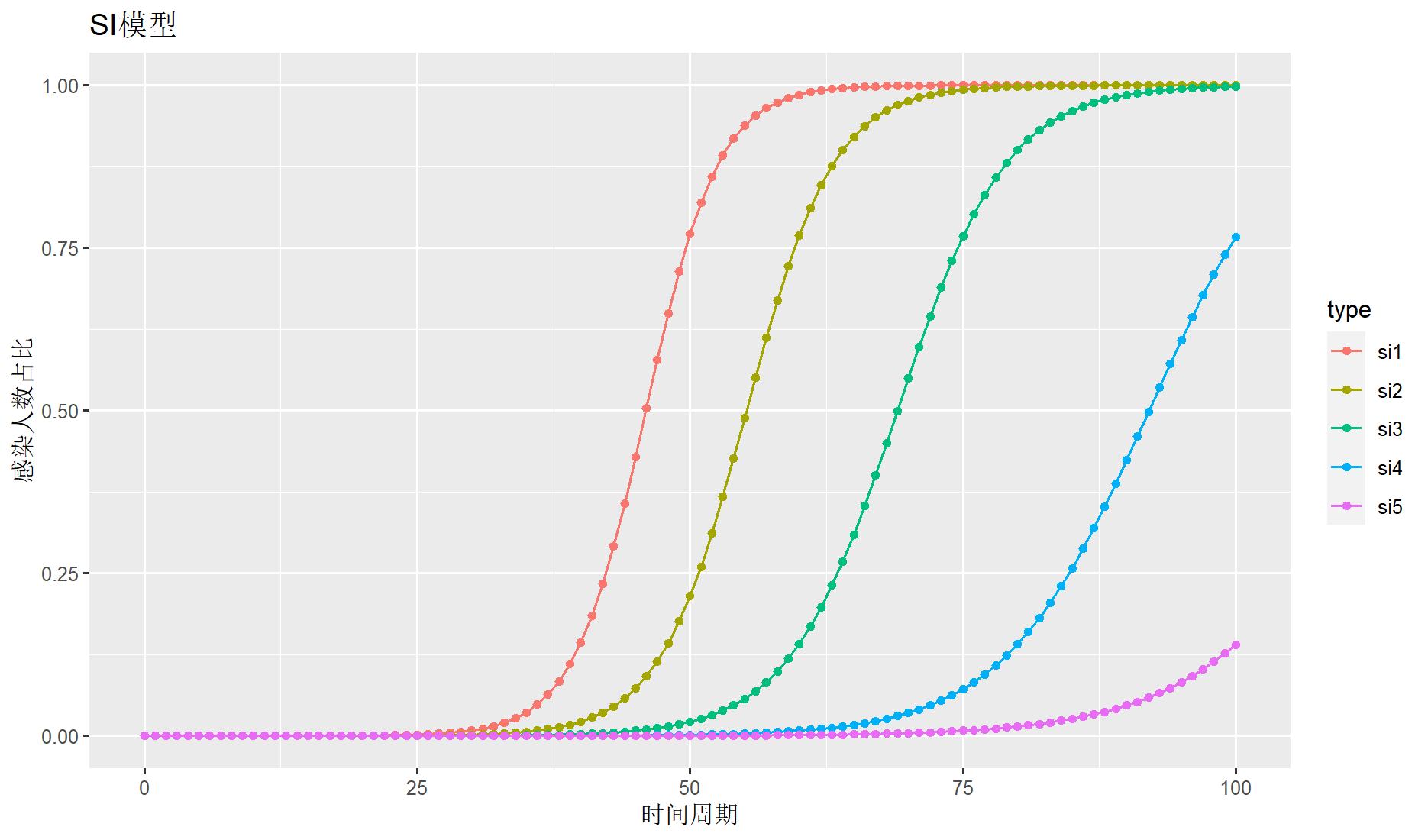
分别计算当传播率ρ(rio)为0.3,0.25,0.2,0.15,0.12时的结果,已感染者比例𝑖0 =0.000001(百万分之一)
> si1 <- calc2(rio = 0.3)
> si2 <- calc2(rio = 0.25)
> si3 <- calc2(rio = 0.2)
> si4 <- calc2(rio = 0.15)
> si5 <- calc2(rio = 0.12)
> sdf2<-rbinddf(list(si1,si2,si3,si4,si5),
+ names=c("si1","si2","si3","si4","si5"))
> names(sdf2)<-c("time","value","type")
# 画图
> draw(sdf2,title="SI模型",ylab="感染人数占比",xlab="时间周期")
4. SIS模型
人群分为易感染者(Susceptible)和已感染者(Infective)两类,已感染者(Infective)可以被治愈,变成易感染者(Susceptible)(称之为SIS模型)。SIS模型与SI模型的差异,在于SIS模型假设已感染者(Infective)可以被治愈,重新变成易感染者(Susceptible),比如季节性流感等。
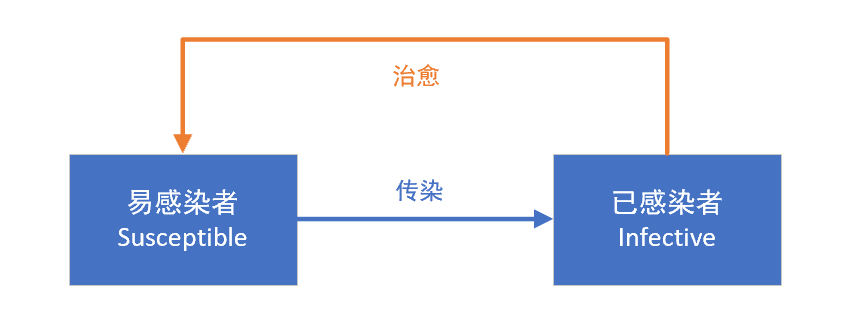
1、传染的速度,取决于病人的传染速度,与病人的治愈速度之间的相对水平,如果病人的治愈速度,大于病人的传染速度,即μ>ρ,那么该传染病最终会消失;
2、即便病人的传染速度高于治愈速度,最终也只有一部分人群会被感染;
3、最终感染的人群比例,为1-1/sigma,sigma = ρ / μ ,sigma是整个传染期内每个病人的有效接触人数,可以理解为病人在整个生病期内,接触的总人数。
模型假设
- 在疾病传播期内所考察地区的总人数不变,不考虑生死和迁移。
- 当病人与健康者有效接触时,使健康者受感染变为病人。
- 人被全部治愈,所需要的天数为1/μ,为传染病的平均传染期。
模型构建:
已感染人数为 N * i(t),所有已感染人每天有效接触人数为 ρ * N * i(t),其中被传染的易感染人的比例 s(t),因此每天增加的感染者人数为 ρ * N * i(t) * s(t)。被治愈的人数为 μ * N * i(t)。
- N:总人数,不变
- s(t):t时刻易感染者在总人数中所占比例。
- i(t):t时刻已感染者在总人数中所占比例。
- ρ是常数,每个病人每天有效接触的平均人数是常数,为日接触率, ρ >0
- μ是常数,每天被治愈的病人数占病人总数的比例,为日治愈率
从t到t+Δt的时间里,病人增加的人数为
N * (i(t+Δt)– i(t)) = ρ * i(t) * s(t) * Δt – μ * N * i(t) * Δt
模型求解:
- N总人数不变,因此 s(t) + i(t) = 1
- 当t=0时,初始病人占比为 i0 得,
𝑑𝑖/𝑑𝑡= ρ * i * (1-i) – μ * i
i(0) = 𝑖0
编写模型内核函数。
> calc3 <- function(rio = 0.3, # 接触率,传染率系数
+ mu=0.1, # 治愈率
+ times = 0:150, # 病情发展时间
+ i = 0.000001) { # 已感染者初始占比:百万分之一
+ sis_equations<-function(time,vars,params){
+ with(as.list(c(vars,params)),{
+ di<-rio*i*(1-i)-mu*i
+ return(list(c(di)))
+ })
+ }
+
+ ode(
+ func=sis_equations,
+ y=c(i=i),
+ times=times,
+ parms=c(rio=rio,mu=mu)
+ ) %>% as.data.frame()
+ }
分别日接触率 ρ(rio) = 0.3、0.25、0.2、0.15、0.12,日治愈率 μ =0.1,已感染者比例 𝑖0 =0.000001(百万分之一)
> sis1 <- calc3(rio = 0.27,mu=0.1)
> sis2 <- calc3(rio = 0.25,mu=0.1)
> sis3 <- calc3(rio = 0.20,mu=0.1)
> sis4 <- calc3(rio = 0.15,mu=0.1)
> sis5 <- calc3(rio = 0.12,mu=0.1)
> sdf<-rbinddf(list(sis1,sis2,sis3,sis4,sis5),
+ names=c("sis1","sis2","sis3","sis4","sis5"))
> names(sdf)<-c("time","value","type")
> draw(sdf,title="SIS模型",ylab="感染人数占比",xlab="时间周期")
5. SIR模型
人群分为易感染者(Susceptible)和已感染者(Infective)和恢复者(Removed)三类(称之为SIR模型)。SIR模型与SIS模型的差异,在于SIR模型假设已感染者(Infective)被治愈后会具备免疫力,不会被感染,从而成为恢复者(Removed),SIR模型已经初步接近实际的传染病模型。

模型假设:
- 在疾病传播期内所考察地区的总人数不变,不考虑生死和迁移。
- 当病人与健康者有效接触时,使健康者受感染变为病人。
- 人被全部治愈,所需要的天数为1/μ,为传染病的平均传染期。
模型构建:
已感染人数为 N * i(t),已感染人每天有效接触人数为 ρ * I(t),被传染的易感染人的比例 S(t)/N,因此每天增加的感染者人数为 ρ * I(t) * S(t)/N,被治愈的人数为 μ * I(t)。
- N:总人数,不变
- S(t):t时刻易感染者在总人数中所占比例。
- I(t):t时刻已感染者在总人数中所占比例。
- R(t): t时刻恢复者在总人数中所占比例。
- ρ是常数,每个病人每天有效接触的平均人数是常数,为日接触率, ρ >0
- μ是常数,每天被治愈的病人数占病人总数的比例,为日治愈率
从t到t+Δt的时间里,易感染者人数,已感染者人数,恢复者人数计算:
# 易感染者人数计算
S(t+ Δt) – S(t) = - ρ * I(t) * Δt/N
# 已感染者人数计算
I(t+ Δt) – I(t) = ρ * I(t) * S(t) * Δt/N - μ * I(t) * Δt
# 恢复者人数计算
R(t+ Δt) – R(t) = μ * I(t) * Δt
模型求解:
- N总人数不变,因此 s(t) + i(t) = 1
- 当t=0时,初始病人占比为 i0 得,
𝑑𝑆/𝑑𝑡= -ρ * I * S/N
𝑑𝐼/𝑑𝑡= ρ * I * S/N – μ * I
𝑑𝑟/𝑑𝑡= μ * I
编写模型内核函数。
> calc4 <- function(rio = 0.3, # 接触率,传染率系数
+ mu=0.1, # 治愈率
+ times = 0:150, # 病情发展时间
+ S=1000*1000*10, # 易感染者1000万人
+ I=10, # 已感染者10人
+ R=5) { # 已移出者5人
+ sir_equations<-function(time,vars,params){
+ with(as.list(c(vars,params)),{
+ N<-S+I+R
+ dS<- -rio*I*S/N
+ dI<-rio*I*S/N - mu*I
+ dR<-mu*I
+ return(list(c(dS,dI,dR)))
+ })
+ }
+ ode(
+ func=sir_equations,
+ y=c(S=S,I=I,R=R),
+ times=times,
+ parms=c(rio=rio,mu=mu)
+ ) %>% as.data.frame()
+ }
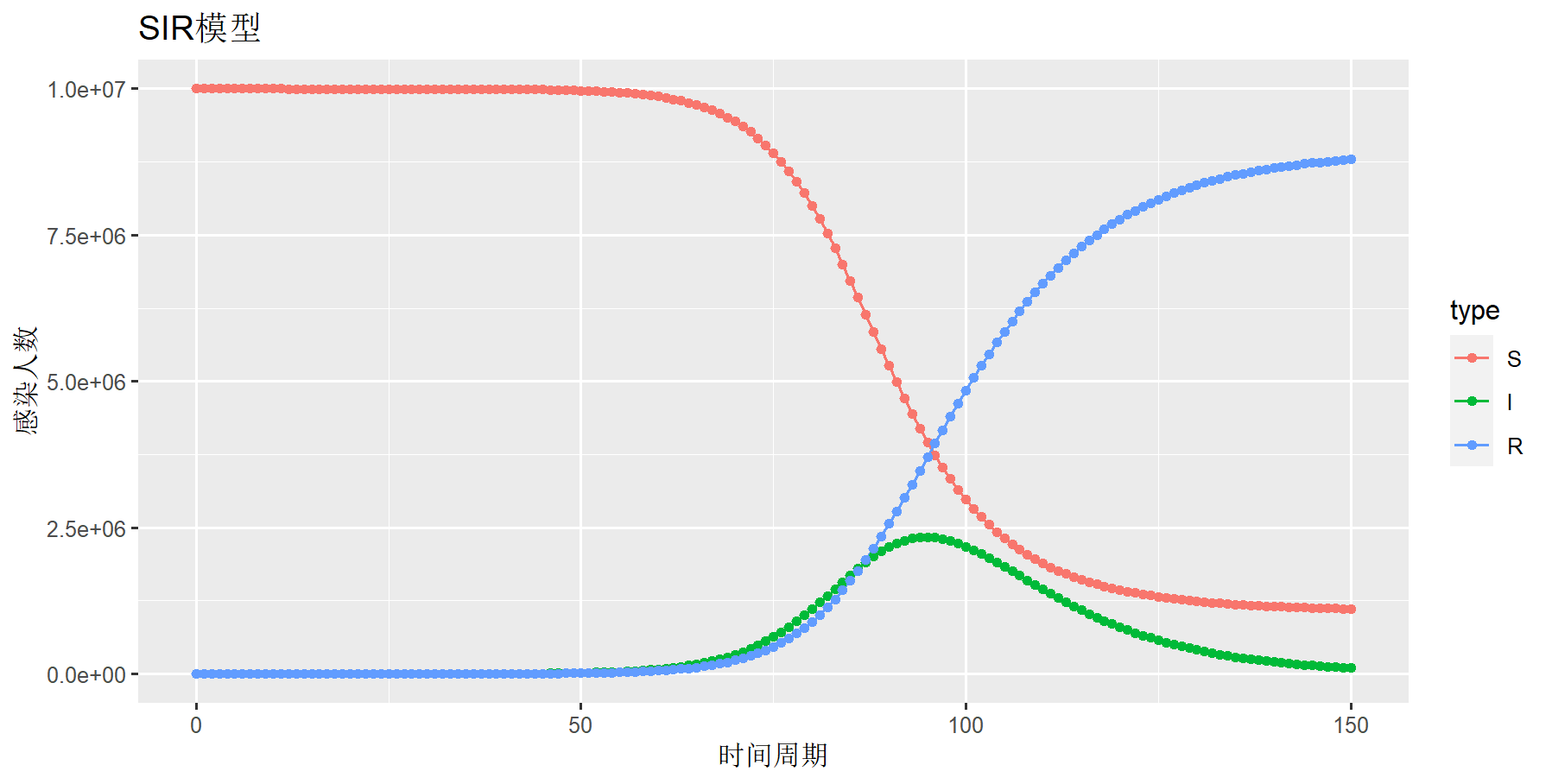
当日接触率ρ(rio) = 0.25,日治愈率 μ(mu) =0.1,易感染者S=1000*1000*10,已感染者 I=10,移出者R=100
> sir1<-calc4(rio=0.25,mu=0.1,times=0:150,S=1000*1000*10,I=10,R=100)
> head(sir1)
time S I R
1 0 10000000 10.00000 100.0000
2 1 9999997 11.61831 101.0789
3 2 9999994 13.49852 102.3324
4 3 9999991 15.68299 103.7887
5 4 9999986 18.22099 105.4808
6 5 9999981 21.16971 107.4466
> sdf4<-melt(sir1,id.vars = c("time"))
> head(sdf4)
time variable value
1 0 S 10000000
2 1 S 9999997
3 2 S 9999994
4 3 S 9999991
5 4 S 9999986
6 5 S 9999981
> names(sdf4)<-c("time","type","value")
> draw(sdf4,title="SIR模型",ylab="感染人数",xlab="时间周期")
通过对传播病动力学的基本模型学习,让我了解了传染病的传播基本知识,使我更加坚信坚持“动态清零”的意义是重大的。文本以手写R代码实现模型为主,下一篇文章:用专业工具EpiModel玩转传染病模型
参考文章:
文本完整的代码,已经上传github,可以自由下载使用:https://github.com/bsspirit/infect/blob/main/code/model.r
转载请注明出处:
http://blog.fens.me/r-infectious-disease