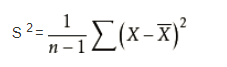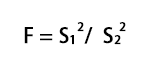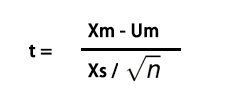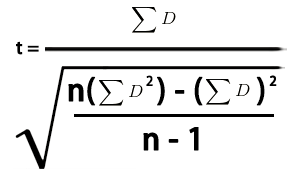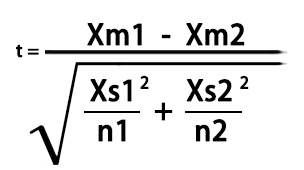R的极客理想系列文章,涵盖了R的思想,使用,工具,创新等的一系列要点,以我个人的学习和体验去诠释R的强大。
R语言作为统计学一门语言,一直在小众领域闪耀着光芒。直到大数据的爆发,R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入,R语言的社区在迅速扩大成长。现在已不仅仅是统计领域,教育,银行,电商,互联网….都在使用R语言。
要成为有理想的极客,我们不能停留在语法上,要掌握牢固的数学,概率,统计知识,同时还要有创新精神,把R语言发挥到各个领域。让我们一起动起来吧,开始R的极客理想。
关于作者:
- 张丹,分析师/程序员/Quant: R,Java,Nodejs
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-stat-anova/
前言
方差分析是一种基本统计学方法,在众多领域都有非常广泛的应用,比如评估不同药物的疗效,不同的广告策略的效果。
大模型的时代,是否能用方差分析,判断大模型结论与实际结论,是否有显著性差异,那么就能够快速验证大模型的是否产生了幻觉,以此来对大模型进行改进。
目录
- 方差分析介绍
- 用R语言方差分析aov()函数
- 用R语言方进行方差分析
1. 方差分析介绍
方差分析(Analysis of Variance,简称ANOVA)是一种用于比较多个群体均值是否存在显著差异的统计方法。它通过分析数据中不同来源的变异来检验均值差异的显著性。
方差分析的核心思想是将总变异分解为,组间变异(不同处理组之间的差异)和组内变异(同一组内的个体差异),通过比较这两种变异的相对大小来判断均值差异是否显著。
方差分析的主要类型为,
- 单因素方差分析(One-way ANOVA):比较一个分类自变量(因素)对连续因变量的影响,例如:比较三种不同教学方法对学生成绩的影响
- 双因素方差分析(Two-way ANOVA):同时考察两个分类自变量对连续因变量的影响,可以分析主效应和交互效应,例如:研究性别(男/女)和教学方法(A/B/C)对学生成绩的共同影响
- 多元方差分析(MANOVA):适用于多个连续因变量的情况
ANOVA的核心目标是区分数据变异性的来源:是由实验条件(或处理)的不同引起的,还是由随机变异(即自然波动或实验误差)引起的。这种区分有助于我们判断实验条件是否对研究变量有显著影响。
ANOVA的关键组成部分
- 总方差(Total Variance): 数据总体的方差,包括组间方差和组内方差。
- 组间方差(Between-Group Variance): 不同组(或处理条件)间均值的差异。
- 组内方差(Within-Group Variance): 同一组内个体间的差异。
通过比较组间方差和组内方差,ANOVA帮助我们判断各组间是否存在显著的均值差异。如果组间方差显著大于组内方差,我们有理由相信不同组的均值存在显著差异。
方差分析的基本假设
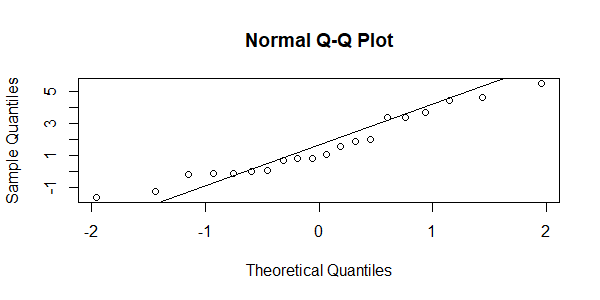
- 正态性:每个组的数据应近似呈正态分布。这意味着数据的分布应该是对称的,没有明显的偏斜,使用Shapiro-Wilk检验
- 方差齐性:所有组的方差应该大致相等。这个假设确保了不同组别的数据具有一致的波动性,使用Levene’s Test或Bartlett’s Test来检验
- 独立性:数据点之间应该是相互独立的,即一个数据点的值不应影响或决定另一个数据点的值。
方差分析步骤
- 提出假设:零假设(H₀):所有组的均值相等,即组间不存在显著差异。备择假设(H₁):至少有两组的均值不等,即存在至少一个组间的显著差异。
- 计算组间和组内方差:组间方差(Between-Group Variance):计算每个组的均值与总体均值之间的差异,反映了不同处理或条件下数据的变化程度。组内方差(Within-Group Variance):计算组内数据点与各自组均值的差异,表示在相同条件下的数据波动。
- 计算F统计量:F值是方差分析中的核心统计量,它是组间方差与组内方差的比率:F = 组间方差 / 组内方差 ,较高的F值通常表明组间存在显著差异。但我们需要通过F分布来确定这个差异是否统计上显著。
- 将计算得到的F值与临界值比较,或直接看p值,根据自由度和显著性水平(通常是0.05)找到F值的临界值。如果计算出的F值超过临界值,我们拒绝零假设,认为至少有两组间存在显著差异。
- 做出统计决策
事后检验:当方差分析结果显示显著差异时,需要进行事后检验(Post-hoc tests)来确定具体哪些组之间存在差异,常用方法包括:Tukey’s HSD检验,Bonferroni校正,Scheffe检验。
2. 用R语言方差分析aov()函数
R中的方差分析(ANOVA)是一种统计方法,用于比较两个或多个组之间的均值是否存在显著差异。在R语言中,可以使用ANOVA函数(aov)进行方差分析。
在R语言中,自带的stat包的aov()函数,就是我们最常用方差分析的计算函数。
aov()函数的语法为aov(formula, data=dataframe),y是因变量,字母ABC代表因子。
R语言代码的写法:
model <- aov(response ~ group, data = dataset)
summary(model)
| 符号 | 用途 |
|---|---|
| ~ | 分隔符号,左边为响应变量(因变量),右边为解释变量(自变量),如 y ~ A + B + C |
| : | 表示预测变量的交互项,A与B的交互,如y ~ A + B + A:B |
| * | 表示所有可能交互项的简洁方式,如 y ~ A*B*C 等同于 y ~ A+B+C + A:B + A:C + B:C + A:B:C |
| ^ | 表示交互项达到某个次数,如y~(A+B+C)^2 等同于 y~ A+B+C + A:B + A:C + B:C |
| . | 表示包含除因变量外的所有变量,如y~. 等同于 y~ A+B+C |
下面是常见研究设计的表达式
| 设计 | 表达式 |
|---|---|
| 单因素ANOVA | y ~ A |
| 含单个协变量的单因素ANOVA | y ~ x + A |
| 双因素ANOVA | y ~ A * B |
| 含两个协变量的双因素ANOVA | y ~ x1 + x2 + A * B |
| 随机化区组 | y ~ B + A (B是区组因子) |
| 单因素组内ANOVA | y ~ A + Error(subject/A) |
| 含单个组内因子(W)和单个组间因子的重复测量ANOVA | y ~ B * W + Error(Subject/W) |
3. R语言实现方差分析
数据集使用datarium包的职位满意度调查jobsatisfaction数据集。
# 安装datarium
> install.packages("datarium")
# 加载程序包
> library(datarium)
> library(dplyr)
查看jobsatisfaction数据集的基本情况,共4列,ID,gender性别,education_level学历水平,score得分。
> data("jobsatisfaction", package = "datarium")
> jobsatisfaction
# A tibble: 58 × 4
id gender education_level score
1 1 male school 5.51
2 2 male school 5.65
3 3 male school 5.07
4 4 male school 5.51
5 5 male school 5.94
6 6 male school 5.8
7 7 male school 5.22
8 8 male school 5.36
9 9 male school 4.78
10 10 male college 6.01
# ℹ 48 more rows
# ℹ Use `print(n = ...)` to see more rows
# 查看统计概率
> summary(jobsatisfaction)
id gender education_level score
1 : 1 male :28 school :19 Min. : 4.780
2 : 1 female:30 college :19 1st Qu.: 5.800
3 : 1 university:20 Median : 6.380
4 : 1 Mean : 6.963
5 : 1 3rd Qu.: 8.515
6 : 1 Max. :10.000
对数据集进行分组gender, education_level,计算均值和标准差
> jobsatisfaction %>%
+ group_by(gender, education_level) %>%
+ get_summary_stats(score, type = "mean_sd")
# A tibble: 6 × 6
gender education_level variable n mean sd
1 male school score 9 5.43 0.364
2 male college score 9 6.22 0.34
3 male university score 10 9.29 0.445
4 female school score 10 5.74 0.474
5 female college score 10 6.46 0.475
6 female university score 10 8.41 0.938
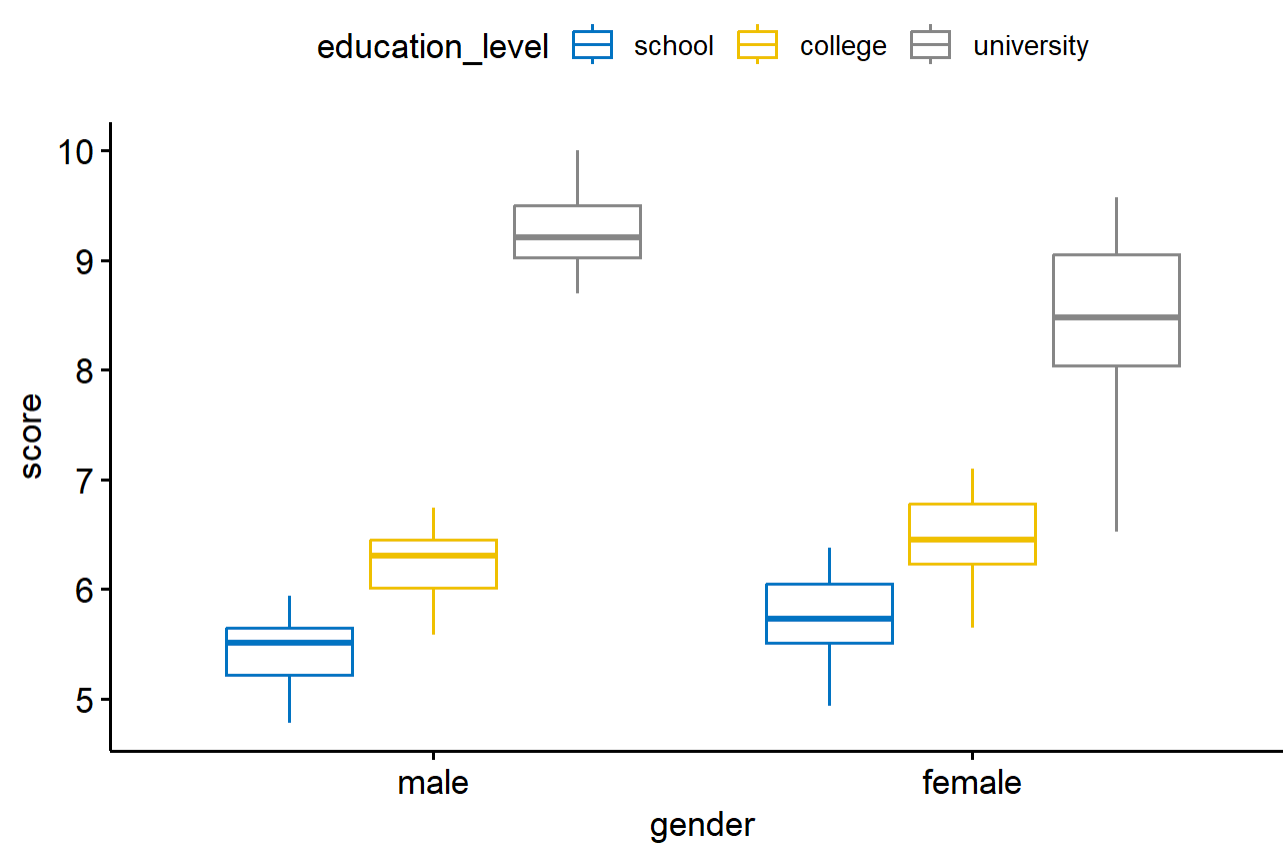
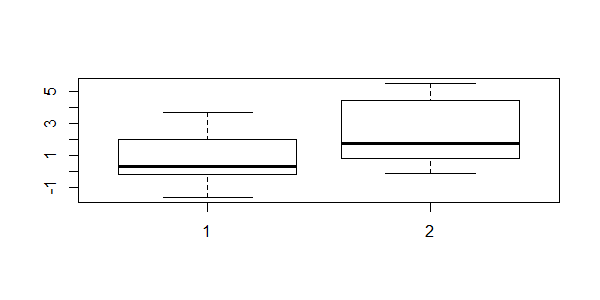
画出分组的数据分箱图
> ggboxplot(
+ jobsatisfaction, x = "gender", y = "score",
+ color = "education_level", palette = "jco"
+ )
建立方差分析模型,有几个变量我们就全部都加入分析,以score为因变量,以gender和education_level的组合为自变量。
# 建模
> model<- aov(score ~ gender*education_level, data = jobsatisfaction)
# 查看因子显著性水平
> summary(model)
Df Sum Sq Mean Sq F value Pr(>F)
gender 1 0.54 0.54 1.787 0.18709
education_level 2 113.68 56.84 187.892 < 2e-16 ***
gender:education_level 2 4.44 2.22 7.338 0.00156 **
Residuals 52 15.73 0.30
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
其中,education_level和gender:education_level的P值对score有影响,gender没有影响。
对模型进行正态分布检验shapiro.test,p值大于0.05,说明符合正态分布。
> shapiro.test(residuals(model))
Shapiro-Wilk normality test
data: residuals(model)
W = 0.96786, p-value = 0.1267
进行方差齐性检验bartlett.test,p值小于0.05,说明education_level方差有显著地不同,方差不是齐性的。
> bartlett.test(score ~ education_level, data = jobsatisfaction)
Bartlett test of homogeneity of variances
data: score by education_level
Bartlett's K-squared = 11.651, df = 2, p-value = 0.002951
进行方差齐性检验bartlett.test,p值大于0.05,说明gender方差没有显著地不同,方差是齐性的。
> bartlett.test(score ~ gender, data = jobsatisfaction)
Bartlett test of homogeneity of variances
data: score by gender
Bartlett's K-squared = 2.3701, df = 1, p-value = 0.1237
Bartlett's K-squared:Bartlett's K-squared是Bartlett检验的统计量,用于衡量不同组间方差的差异。它是通过计算各组的方差并比较它们之间的差异而得出的。如果各组方差相等,则K-squared值应较小;如果方差不相等,K-squared值则较大。
df(自由度):自由度(degrees offreedom,df)是统计分析中的一个重要概念,它指的是在计算某个统计量时,可以自由变化的数值的数量。在上面 Bartlett检验中,由于假设有三个不同种族的组来比较它们之间的出生体重(bwt)的方差,自由度等于组数减一(这里为2)。
p-value(p值):p值用于衡量观察到的统计量在假设检验中的极端性。具体来说,它表示在零假设为真的情况下,观察到像样或更极端结果的概率。若p值小于某个显著性水平(通常为0.05),则我们拒绝零假设;若p值大于显著性水平,则不能拒绝零假设。在Bartlett检验中,p值大于0.05表示没有足够的证据表明各组间方差存在显著差异。
使用Tukey’s HSD检验,进行分组的显著差异。
> TukeyHSD(model)
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = score ~ gender * education_level, data = jobsatisfaction)
$gender
diff lwr upr p adj
female-male -0.1932143 -0.4832329 0.09680436 0.1870895
$education_level
diff lwr upr p adj
college-school 0.7573684 0.3268386 1.187898 0.0002637
university-school 3.2518102 2.8266960 3.676924 0.0000000
university-college 2.4944417 2.0693275 2.919556 0.0000000
$`gender:education_level`
diff lwr upr
female:school-male:school 0.3143333 -0.433358082 1.0620247
male:college-male:school 0.7966667 0.029551460 1.5637819
female:college-male:school 1.0363333 0.288641918 1.7840247
male:university-male:school 3.8653333 3.117641918 4.6130247
female:university-male:school 2.9793333 2.231641918 3.7270247
male:college-female:school 0.4823333 -0.265358082 1.2300247
female:college-female:school 0.7220000 -0.005749384 1.4497494
male:university-female:school 3.5510000 2.823250616 4.2787494
female:university-female:school 2.6650000 1.937250616 3.3927494
female:college-male:college 0.2396667 -0.508024749 0.9873581
male:university-male:college 3.0686667 2.320975251 3.8163581
female:university-male:college 2.1826667 1.434975251 2.9303581
male:university-female:college 2.8290000 2.101250616 3.5567494
female:university-female:college 1.9430000 1.215250616 2.6707494
female:university-male:university -0.8860000 -1.613749384 -0.1582506
p adj
female:school-male:school 0.8132166
male:college-male:school 0.0374890
female:college-male:school 0.0019203
male:university-male:school 0.0000000
female:university-male:school 0.0000000
male:college-female:school 0.4086560
female:college-female:school 0.0529764
male:university-female:school 0.0000000
female:university-female:school 0.0000000
female:college-male:college 0.9317495
male:university-male:college 0.0000000
female:university-male:college 0.0000000
male:university-female:college 0.0000000
female:university-female:college 0.0000000
female:university-male:university 0.0087499
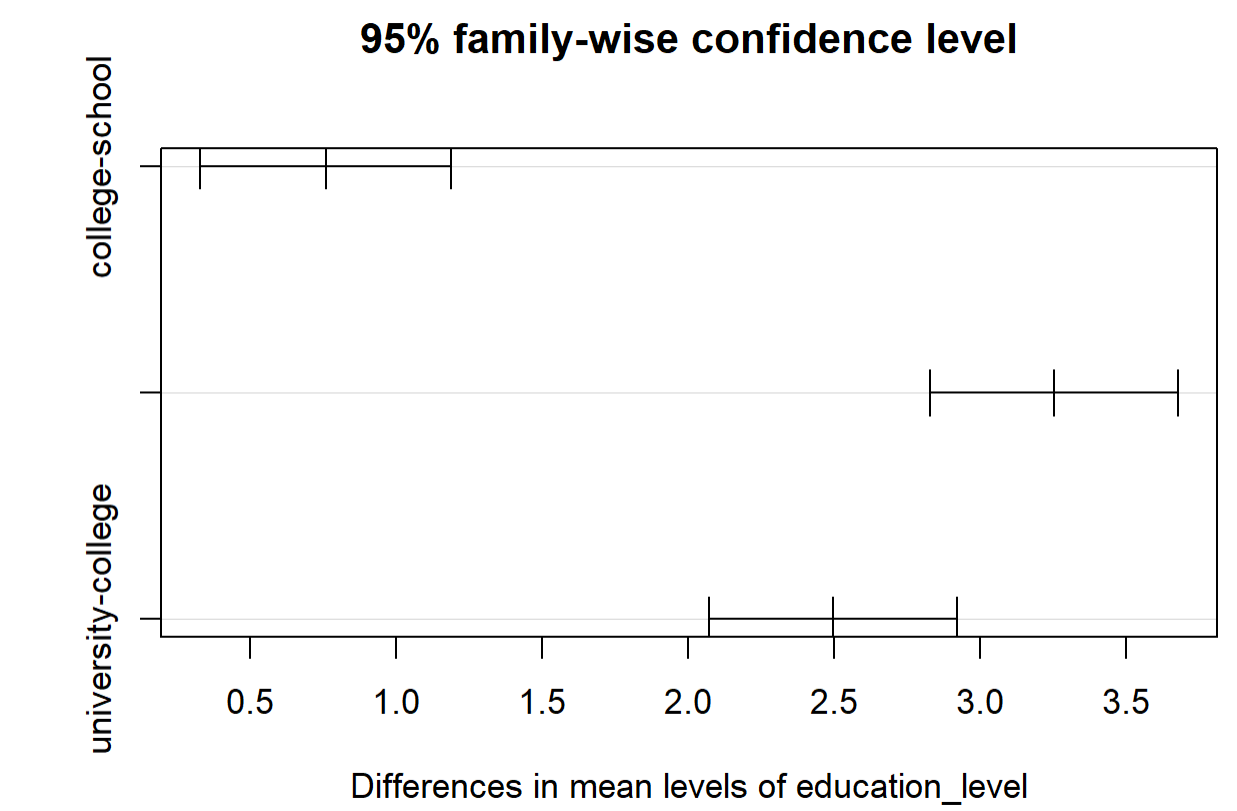
TukeyHSD的检验,education_level的显著性水平最高,所以我们画出education_level检验图。
> plot(TukeyHSD(model, "education_level"))
本文通过方差分析,实现对不同变量的影响权重的计算,可以通过统计学的方法,发现新的变量特征。
转载请注明出处:
http://blog.fens.me/r-stat-anova/