R的极客理想系列文章,涵盖了R的思想,使用,工具,创新等的一系列要点,以我个人的学习和体验去诠释R的强大。
R语言作为统计学一门语言,一直在小众领域闪耀着光芒。直到大数据的爆发,R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入,R语言的社区在迅速扩大成长。现在已不仅仅是统计领域,教育,银行,电商,互联网….都在使用R语言。
要成为有理想的极客,我们不能停留在语法上,要掌握牢固的数学,概率,统计知识,同时还要有创新精神,把R语言发挥到各个领域。让我们一起动起来吧,开始R的极客理想。
关于作者:
- 张丹,分析师/程序员/Quant: R,Java,Nodejs
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-binary-octal-hexadecimal/
在用计算机进行数据计算时,避免不少会涉及到进制的转换操作,从十进制转换到二进制,从十进制转换到十六进制等,转换的过程,其实就是数学计算的过程。本文我们就利用R语言进行进制转换的实现。
目录
- 二进制八进制十六进制
- 转换十进制
- 十进制转换非十进制
1. 二进制八进制十六进制
数制,是一种计数的方法,是用一组固定的符号和统一的规则来表示数值的方法。在计数过程中采用进位的方法称为进位计数制(进制),包括数位、基数和位权三个要素。
- 数位:指数字符号在一个数中所处的位置。
- 基数:指在某种进位计数制中数位上所能使用的数字符号的个数。例如十进制的基数为10
- 位权:数制中某一位上的1所表示数值的大小(所处位置的价值)。例如十进制的230,1的位权是100,2的位权是10,3的位权是1。
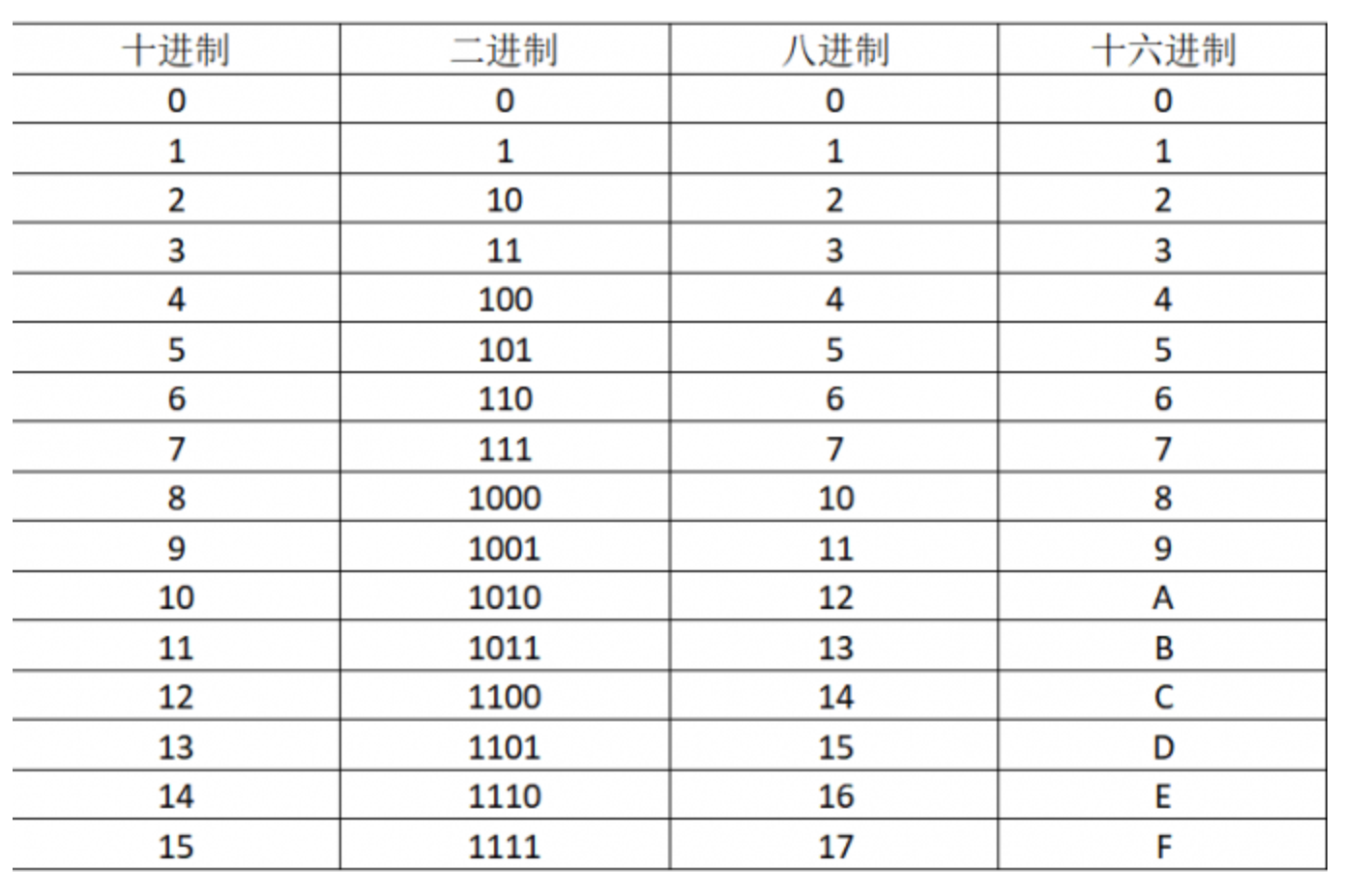
在计算机编程中,常用到的进制有二进制,八进制,十进制,十六进制。
进制数下标表示举例组成说明
| 二进制 | 2、B | (10)₂=10B | 0,1 | Binary:二进制 |
| 八进制 | 8、O、Q | (10)₈=10O=10Q | 0,1,2,3,4,5,6,7 | Octal:八进制,字母O与数学0容易混淆,常用Q替代 |
| 十进制 | 10、D | (10)₁₀=10D | 0,1,2,3,4,5,6,7,8,9 | Decimal:十进制 |
| 二进制 | 16、H | (10)₁₆=10H | 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F | Hexadeciaml:十六进制 |
2. 转十进制计算方法
2.1 二进制转十进制
二进制转为十进制要从右到左用二进制的每个数去乘以2的相应次方,小数点后则是从左往右。
计算举例:(0010)₂ 转十进制 为(2)₁₀
| 二进制 | 0 | 0 | 1 | 0 |
| 2的幂 | 2³ | 2² | 2¹ | 2⁰ |
(101)₂ = 1 * 2² + 0 * 2¹ + 1 * 2 ⁰ = 4 + 0 + 1 = (5)₁₀
(1110)₂ = 1 * 2³ + 1 * 2² + 1 * 2¹ + 0 * 2⁰ = 8 + 4 + 2 + 0 = (14)₁₀
(0010)₂ = 0 * 2³ + 0 * 2² + 1 * 2¹ + 0 * 2⁰ = 0 + 0 + 2 + 0 = (2)₁₀
R语言实现,使用strtoi()函数,可以把二进制的字符串,转为十进制的数值。
> strtoi(c("101", "1110", "0010"), 2L)
[1] 5 14 2
2.2 八进制转十进制
八进制转为十进制要从右到左用八进制的每个数去乘以8的相应次方,小数点后则是从左往右。
计算举例:
(375)₈ = 3 * 8² + 7 * 8¹ + 5 * 8 ⁰ = 192 + 56 + 5 = (253)₁₀
(1110)₈ = 1 * 8³ + 1 * 8² + 1 * 8¹ + 0 * 8⁰ = 512 + 64 + 8 + 0 = (584)₁₀
R语言实现
> strtoi(c("375", "1110"), 8L)
[1] 253 584
2.3 十六进制转十进制
十六进制转为十进制要从右到左用八进制的每个数去乘以16的相应次方,小数点后则是从左往右。
计算举例:
(10A)₁₆ = 1 * 16² + 0 * 16¹ + 10 * 16 ⁰ = 256 + 0 + 10 = (266)₁₀
(111F)₁₆ = 1 * 16³ + 1 * 16² + 1 * 16¹ + 15 * 16⁰ = 4096 + 256 + 16 + 15 = (4383)₁₀
R语言实现
> strtoi(c("10A","111F"), 16L)
[1] 266 4383
3. 十进制转换非十进制计算方法
使用辗转相除法:
- 整数部分:整数除以进制数(2,8,10,16),倒取余数,直到整数为0。
- 小数部分:小数乘以进制数(2,8,10,16),正取整数,直接小数为0。
以 十进制转二进制为例,分为整数转二进制,和小数转二进制。
3.1 整数转二进制:
采用”除2取余,逆序排列”法:
- 用2整除一个十进制整数,得到一个商和余数
- 然后再用2去除得到的商,又会得到一个商和余数
- 重复操作,一直到商为小于1时为止
- 然后将得到的所有余数全部排列起来,再将它反过来逆序排列。
计算举例:
计算(5)₁₀的二进制。
| 计算 | 商 | 余 | 位置 |
| 5/2 | 2 | 1 | 1 |
| 2/2 | 1 | 0 | 2 |
| 1/2 | 0 | 1 | 3 |
(5)₁₀ = 反转(5%2, 2%2, 1%2) = 反转(1,0,1) = (101)₂
计算(42)₁₀的二进制。
| 计算 | 商 | 余 | 位置 |
| 42/2 | 21 | 0 | 1 |
| 21/2 | 10 | 1 | 2 |
| 10/2 | 5 | 0 | 3 |
| 5/2 | 2 | 1 | 4 |
| 2/2 | 1 | 0 | 5 |
| 1/2 | 0 | 1 | 6 |
(42)₁₀ = 反转(42%2 , 21%2 , 10%2 , 5%2, 2%2, 1%2) = 反转(0,1,0,1,0,1 ) = (101010)₂
R语言实现,我们可以使用intToBits()函数,输入十进制整数,会得到二进制的结果。
> intToBits(5)
[1] 01 00 01 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
[20] 00 00 00 00 00 00 00 00 00 00 00 00 00
> intToBits(42)
[1] 00 01 00 01 00 01 00 00 00 00 00 00 00 00 00 00 00 00 00
[20] 00 00 00 00 00 00 00 00 00 00 00 00 00
因为计算机内部表示数的字节单位是定长的,如8位、16位、32位。所以位数不够时,高位补零。R语言intToBits(),int是32位的,因此出现了大量的补的位数。
intToBits()函数输出结果非常长,不太利于阅读,我们可以改造一下显示。创建一个intToBitString()函数,把二进制的intToBits()结果转为字符串进行输出,同时去掉多余的0。
> intToBitString<-function(num){
+ a<-as.integer(intToBits(num))
+ a<-a[1:max(which(a==1))] + paste(rev(a), collapse = "") + } # 输出二进制结果 > intToBitString(5)
[1] "101"
> intToBitString(42)
[1] "101010"
3.2 小数转二进制:
采用”乘2取整,顺序排列”法:
- 用2乘十进制小数,可以得到积,将积的整数部分取出
- 再用2乘余下的小数部分,又得到一个积,再将积的整数部分取出
- 重复操作,直到积中的小数部分为零,此时0或1为二进制的最后一位,或者达到所要求的精度为止
计算举例:
(0.25)₁₀ = (0.25*2, 0.5*2) = (0,1) = (0.01)₂
(0.111)₁₀ = (0.111*2 , 0.222*2 , 0.444*2 , 0.888*2, 0.776*2, 0.552*2, 0.104*2 …) = (0,0,0,1,1,1,0 … ) = (0.000110)₂ 取前7位
(5.25)₁₀ = 反转(5%2, 2%2, 1%2) . (0.25*2, 0.5*2) = (101)₂ .(0.01)₂ = (101.01)₂
用R语言实现,使用numToBits()函数,可以把带小数的数值,转换为64位的二进制数,然后可以用packBits()函数,进行数值还原来十进制数。
> a1<-numToBits(0.25);a1
[1] 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
[20] 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
[39] 00 00 00 00 00 00 00 00 00 00 00 00 00 00 01 00 01 01 01
[58] 01 01 01 01 01 00 00
> packBits(a1,type="double")
[1] 0.25
> a2<-numToBits(0.111);a2
[1] 01 00 00 00 01 00 01 01 00 01 00 00 00 01 00 00 01 01 00
[20] 01 01 00 01 01 01 00 00 01 01 01 01 01 00 01 01 01 01 01
[39] 01 00 00 01 00 01 00 01 01 00 00 00 01 01 01 01 00 01 01
[58] 01 01 01 01 01 00 00
> a3<-numToBits(5.25);a3
[1] 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
[20] 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
[39] 00 00 00 00 00 00 00 00 00 00 01 00 01 00 01 00 00 00 00
[58] 00 00 00 00 00 01 00
> packBits(a3,type="double")
[1] 5.25
本文我们进制转换的数学计算原理和R语言的函数使用,可以很方便的利用不同进制特点,构建自己的计算模型。
转载请注明出处:
http://blog.fens.me/r-binary-octal-hexadecimal/