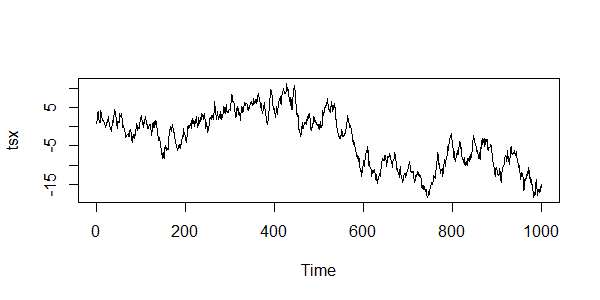R的极客理想系列文章,涵盖了R的思想,使用,工具,创新等的一系列要点,以我个人的学习和体验去诠释R的强大。
R语言作为统计学一门语言,一直在小众领域闪耀着光芒。直到大数据的爆发,R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入,R语言的社区在迅速扩大成长。现在已不仅仅是统计领域,教育,银行,电商,互联网….都在使用R语言。
要成为有理想的极客,我们不能停留在语法上,要掌握牢固的数学,概率,统计知识,同时还要有创新精神,把R语言发挥到各个领域。让我们一起动起来吧,开始R的极客理想。
关于作者:
- 张丹(Conan), 程序员R,Nodejs,Java
- weibo:@Conan_Z
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-ar
前言
时间序列是金融分析中常用到的一种数据格式,自回归模型是分析时间序列数据的一种基本的方法。通过建立自回归模型,找到数据自身周期性的规律,从而帮助我们理解金融市场的发展变化。
在时间序列分析中,有一个常用的模型包括AR,MA,ARMA,ARIMA,ARCH,GARCH,他们的主要区别是适用条件不同,且是层层递进的,后面的一个模型解决了前一个模型的某个固有问题。本文以AR模型做为开始,将对时间序列分析体系,进行完整的介绍,并用R语言进行模型实现。
由于本文为非统计的专业文章,所以当出现与教课书不符的描述,请以教课书为准。本文力求用简化的语言,来介绍自回归模型的知识,同时配合R语言的实现。
目录
- 自回归模型介绍
- 用R语言构建自回归模型
- 模型识别ACF/PACF
- 模型预测
1. 自回归模型(AR)
自回归模型(Autoregressive model),简称AR模型,是统计上一种处理时间序列的方法,用来描述当前值与历史值之间的关系,用变量自身的历史时间数据对自身进行预测,自回归模型必须满足平稳性的要求。比如,时间序列数据集X 的历史各期数据从X1至Xt-1,假设它们为线性关系,可以对当期Xt的表现进行预测。X的当期值等于一个或数个落后期的线性组合,加常数项,加随机误差。
p阶自回归过程的公式定义:
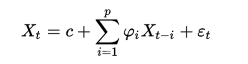
字段解释:
- Xt是当期的X的表现
- c是常数项
- p是阶数,i为从1到p的值
- φi是自相关系数
- t为时间周期
- εt是均值为0,标准差为δ 的随机误差,同时δ是独立于t的
对于一阶自回模型,用AR(1)来表示,简化后的公式为:
![]()
自回归是从线性回归分析中发展而来,只是把自变量x对因变量y的分析,变成自变量x对自身的分析。如果你需要了解线性回归的知识,请参考文章R语言解读一元线性回归模型。
自回归模型的限制
自回归模型是用自身的数据来进行预测,但是这种方法受到一定的限制:
- 必须具有平稳性,平稳性要求随机过程的随机特征不随时间变化。
- 必须具有自相关性,如果自相关系数(φi)小于0.5,则不宜采用,否则预测结果极不准确。
- 自回归只适用于预测与自身前期相关的现象,即受自身历史因素影响较大的现象。对于受其他因素影响的现象,不宜采用自回归,可以改用向量自回归模型。
平稳性时间序列的特点
平稳性要求产生时间序列Y的随机过程的随机特征不随时间变化,则称过程是平稳的;假如该随机过程的随机特征随时间变化,则称过程是非平稳的。
平稳性是由样本时间序列所得到的拟合曲线,在未来的一段期间内能顺着现有的形态能一直地延续下去;如果数据非平稳,则说明样本拟合曲线的形态不具有延续的特点,也就是说拟合出来的曲线将不符合当前曲线的形态。
- 随机变量Yt的均值和方差均与时间t无关
- 随机变量Yt和Ys的协方差只与时间差(步长)t-s有关
- 对于平稳时间序列在数学上有比较丰富的处理手段,非平稳的时间序列通过差分等手段转化为平稳时间序列处理
2. 用R语言构建自回归模型
了解了自回归模型的定义,我们就可以用R语言来模拟一下自回归模型的构建和计算过程。
生成一个随机游走的数据集,满足平稳性的要求。
# 随机游走的数据集
> set.seed(0)
> x<-w<-rnorm(1000) # 生成符合正态分布N(0,1)的数据
> for(t in 2:1000) x[t]<-x[t-1]+w[t]
> tsx<-ts(x) # 生成ts时间序列的数据集
# 查看数据集
> head(tsx,15)
[1] 1.2629543 0.9367209 2.2665202 3.5389495 3.9535909 2.4136409
[7] 1.4850739 1.1903534 1.1845862 3.5892396 4.3528331 3.5538238
[13] 2.4061668 2.1167053 1.8174901
> plot(tsx) # 生成可视化图形
> a<-ar(tsx);a # 进行自回归建模
Call:
ar(x = tsx)
Coefficients:
1
0.9879
Order selected 1 sigma^2 estimated as 1.168
自相关系数为0.9879 ,这是一个非常强的自相关性,所以上述的数列符合自相关的特性。
R语言中ar()函数提供了多种自相关系数的估计,包括"yule-walker", "burg", "ols", "mle", "yw",默认是用yule-walker方法,常用的方法还有最小二乘法(ols),极大似然法(mle)。
我们用最小二乘法,来进行参数估计。
> b<-ar(tsx,method = "ols");b
Call:
ar(x = tsx, method = "ols")
Coefficients:
1
0.9911
Intercept: -0.017 (0.03149)
Order selected 1 sigma^2 estimated as 0.9906
用最小二乘法的计算结果,则自相关系统数为0.9911,截距为-0.017。只有使用最小二乘法进行参数估计的时候,才会有截距。
我们用极大似然法,来进行参数估计。
> d<-ar(tsx,method = "mle");d
Call:
ar(x = tsx, method = "mle")
Coefficients:
1
0.9904
Order selected 1 sigma^2 estimated as 0.9902
用极大似然法计算结果,则自相关系统数为0.9904。对于上面3种估计方法,自相关系数的值都是很接近的。
3. 模型识别ACF/PACF
在上面的例子中,我们默认是用一阶的自回归模型AR(1),进行程序实现的。在实际应用中,自回归模型AR时间序列的阶数P是未知的,必须根据实际数据来决定,就要对AR模型定阶数。常的方法就是利用自相关函数(ACF)和偏自相关函数(PACF)来确定自回归模型的阶数。在ACF/PACF不能确定的情况下,还需要用AIC(Aikaike info Criterion)、BIC(Bayesian information criterion)的信息准则函数来确定阶数。
自回归模型的确立过程,是通过确定阶数,参数估计,再次确定阶数的方法进行判断。自相关函数ACF,用来确定采用自回归模型是否合适。如果自相关函数具有拖尾性,则AR模型为合适模型。偏自相关函数PACF用来确定模型的阶数,如果从某个阶数之后,偏自相关函数的值都很接近0,则取相应的阶数作为模型阶数,偏自相关函数通过截尾性确定阶数。
1. 自相关函数ACF(autocorrelation function)
将一个有序的随机变量序列与其自身相比较,这就是自相关函数在统计学中的定义。每个不存在相位差的序列,都与其自身相似,即在此情况下,自相关函数值最大。如果序列中的组成部分相互之间存在相关性(不再是随机的),则由以下相关值方程所计算的值不再为零,这样的组成部分为自相关。
自相关函数反映了同一序列在不同时序的取值之间的相关程序。
ACF的公式为:
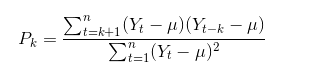
字段解释
- Pk,为ACF的标准误差
- t,为数据集的长度
- k,为滞后,取值从1到t-1,表示相距 k个时间间隔的序列值之间的相关性
- Yt,为样本在t时期的值
- Yt-k,为样本在t-k时期的值
- μ,为样本的均值
所得的自相关值Pk的取值范围为[-1,1],1为最大正相关值,-1则为最大负相关值,0为不相关。
根据上面公式,我们可以手动计算出tsx数据集的ACF值
> u<-mean(tsx) #均值
> v<-var(tsx) #方差
> # 1阶滞后
> p1<-sum((x[1:length(tsx)-1]-u)*(x[2:length(tsx)]-u))/((length(tsx)-1)*v);p1
[1] 0.9878619
> # 2阶滞后
> p2<-sum((x[1:(length(tsx)-2)]-u)*(x[3:length(tsx)]-u))/((length(tsx)-1)*v);p2
[1] 0.9760271
> # 3阶滞后
> p3<-sum((x[1:(length(tsx)-3)]-u)*(x[4:length(tsx)]-u))/((length(tsx)-1)*v);p3
[1] 0.9635961
同时,我们可以用R语言中的acf()函数来计算,会打印前30个滞后的ACF值。
> acf(tsx)$acf
, , 1
[,1]
[1,] 1.0000000
[2,] 0.9878619
[3,] 0.9760271
[4,] 0.9635961
[5,] 0.9503371
[6,] 0.9384022
[7,] 0.9263075
[8,] 0.9142540
[9,] 0.9024862
[10,] 0.8914740
[11,] 0.8809663
[12,] 0.8711005
[13,] 0.8628609
[14,] 0.8544984
[15,] 0.8462270
[16,] 0.8384758
[17,] 0.8301834
[18,] 0.8229206
[19,] 0.8161523
[20,] 0.8081941
[21,] 0.8009467
[22,] 0.7942255
[23,] 0.7886249
[24,] 0.7838154
[25,] 0.7789733
[26,] 0.7749697
[27,] 0.7709313
[28,] 0.7662547
[29,] 0.7623381
[30,] 0.7604101
[31,] 0.7577333
比较前3个值的计算结果,与我们自己的计算结果是一样的,同时可以用R语言进行可视化输出。
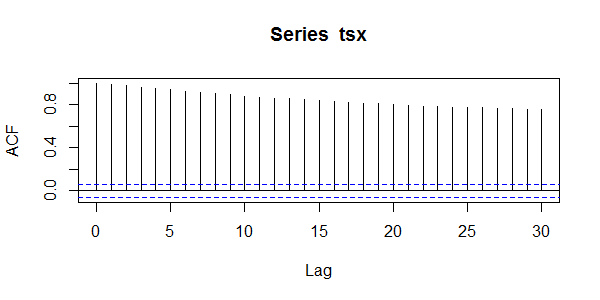
> acf(tsx)
从上图中看出,数据的ACF为拖尾,存在很严重的自相关性。接下来,这时候我们用偏自相关函数确定一下AR的阶数。
2. 偏自相关函数(PACF)(partial autocorrelation function)
偏自相关函数是有自相关函数推到而来。对于一个平稳AR(p)模型,求出滞后k自相关系数p(k)时,实际上得到并不是x(t)与x(t-k)之间单纯的相关关系。因为x(t)同时还会受到中间k-1个随机变量x(t-1)、x(t-2)、……、x(t-k+1)的影响,而这k-1个随机变量又都和x(t-k)具有相关关系,所以自相关系数p(k)里实际掺杂了其他变量对x(t)与x(t-k)的影响。
为了能单纯测度x(t-k)对x(t)的影响,引进偏自相关系数的概念。对于平稳时间序列{x(t)},所谓滞后k偏自相关系数指在给定中间k-1个随机变量x(t-1)、x(t-2)、……、x(t-k+1)的条件下,或者说,在剔除了中间k-1个随机变量x(t-1)、x(t-2)、……、x(t-k+1)的干扰之后,x(t-k)对x(t)影响的相关程度。
简单来说,就是自相关系数ACF还包含了其他变量的影响,而偏自相关系数PACF是严格这两个变量之间的相关性。在ACF中存在着线性关系和非线性关系,偏自相关函数就是把线性关系从自动关系性中消除。当PACF近似于0,表明两个时间点之间的关系性是完全由线性关系所造成的。
通过R语言的pacf()函数来进行偏自相关函数计算。
> pacf(tsx)$acf
, , 1
[,1]
[1,] 0.987861891
[2,] 0.006463542
[3,] -0.030541593
[4,] -0.041290415
[5,] 0.047921168
[6,] -0.009774246
[7,] -0.006267004
[8,] 0.002146693
[9,] 0.028782423
[10,] 0.014785187
[11,] 0.019307564
[12,] 0.060879259
[13,] -0.007254278
[14,] -0.004139848
[15,] 0.015707900
[16,] -0.018615370
[17,] 0.037067452
[18,] 0.019322565
[19,] -0.048471479
[20,] 0.023388065
[21,] 0.027640953
[22,] 0.051177900
[23,] 0.028063875
[24,] -0.003957142
[25,] 0.034030631
[26,] 0.004270416
[27,] -0.029613088
[28,] 0.033715973
[29,] 0.092337583
[30,] -0.031264028
# 可视化输出
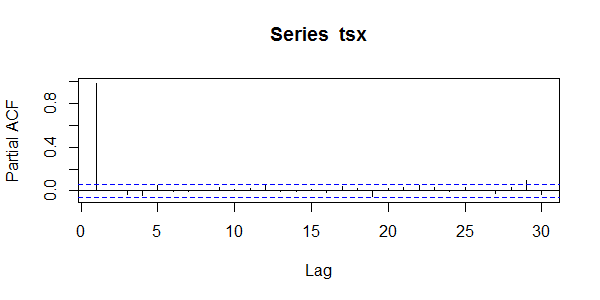
> pacf(tsx)
从上面的这个结果分析,当滞后为1时AR模型显著,滞后为其他值是PACF的值接近于0不显著。所以,对于数据集tsx来说,数据满足AR(1)的自回归模型。对于上文中参数估计出的1阶自相关系数值是可以用的。
4. 模型预测
通过模型识别,我们已经确定了数据集tsx是符合AR(1)的建模条件的,同时我们也创建了AR(1)模型。接下来,就可以利用这个自回测的模型的进行预测,通过规律发现价值。在R语言中,我们可以用predict()函数,实现预测的计算。
使用AR(1)模型进行预测,并保留前5个预测点。
> predict(a,10,n.ahead=5L)
$pred
Time Series:
Start = 2
End = 6
Frequency = 1
[1] 9.839680 9.681307 9.524855 9.370303 9.217627
$se
Time Series:
Start = 2
End = 6
Frequency = 1
[1] 1.080826 1.519271 1.849506 2.122810 2.359189
上面结果中,变量$pred表示预测值,变量$se为误差。
我可以生成可视化的图,更直观的看到预测的结果。
# 生成50个预测值
> tsp<-predict(a,n.ahead=50L)
# 把原数据画图
> plot(tsx)
# 把预测值和误差画出来
> lines(tsp$pred,col='red')
> lines(tsp$pred+tsp$se,col='blue')
> lines(tsp$pred-tsp$se,col='blue')
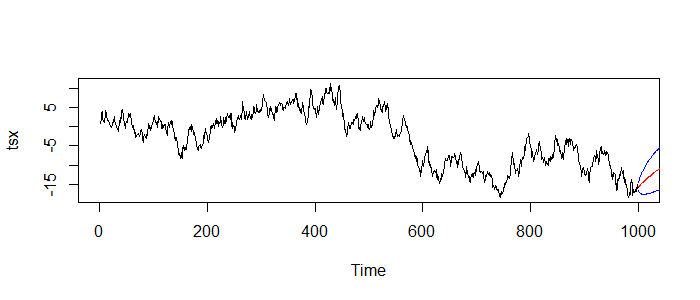
图中,黑色线为原始数据的,红色线为预测值,蓝色线为预测值的范围。这样我们就利用AR(1)模型,实现了对规律的预测计算。
上面关于预测和可视化的过程,我们是通过原生的predict()函数和plot()函数完成的。在R语言中,可以用forecast包来简化上面的操作过程,让代码更少,操作更便捷。
# 加载forecast包
> library('forecast')
# 生成模型AR(1)
> a2 <- arima(tsx, order=c(1,0,0))
> tsp2<-forecast(a2, h=50)
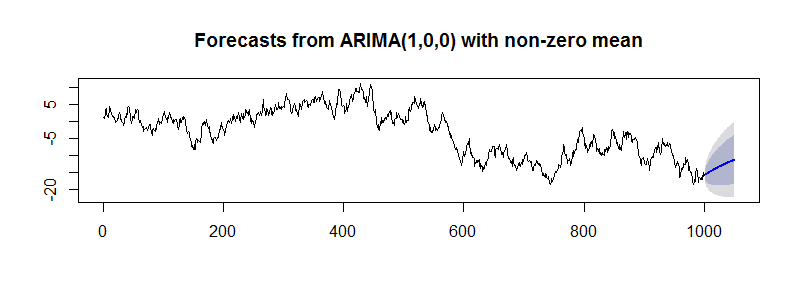
> plot(tsp2)
查看forecast()计算后的预测结果。
> tsp2
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
1001 -15.71590 -16.99118 -14.440628 -17.66627 -13.7655369
1002 -15.60332 -17.39825 -13.808389 -18.34843 -12.8582092
1003 -15.49181 -17.67972 -13.303904 -18.83792 -12.1456966
1004 -15.38136 -17.89579 -12.866932 -19.22685 -11.5358726
1005 -15.27197 -18.06994 -12.474000 -19.55110 -10.9928432
1006 -15.16362 -18.21425 -12.112996 -19.82915 -10.4980922
1007 -15.05631 -18.33593 -11.776682 -20.07206 -10.0405541
1008 -14.95001 -18.43972 -11.460312 -20.28705 -9.6129750
1009 -14.84474 -18.52891 -11.160567 -20.47919 -9.2102846
1010 -14.74046 -18.60591 -10.875013 -20.65216 -8.8287673
1011 -14.63718 -18.67257 -10.601802 -20.80877 -8.4655994
1012 -14.53489 -18.73030 -10.339486 -20.95121 -8.1185723
1013 -14.43357 -18.78024 -10.086905 -21.08123 -7.7859174
1014 -14.33322 -18.82333 -9.843112 -21.20026 -7.4661903
1015 -14.23383 -18.86034 -9.607319 -21.30947 -7.1581923
1016 -14.13538 -18.89190 -9.378864 -21.40985 -6.8609139
通过forecast()函数,直接生成了Forecast值,80%概率的预测值范围,和95%概率的预测值范围。
在明白了整个自回归模型的设计思路、建模过程、检验条件、预测计算、可视化展示的完整操作后,我们就可以真正地把自回归模型用到实际的业务中。发现规律,发现价值!!
自回归模型只是开始,下一篇继续介绍移动平均模型(MA)的建模和使用过程。
转载请注明出处:
http://blog.fens.me/r-ar