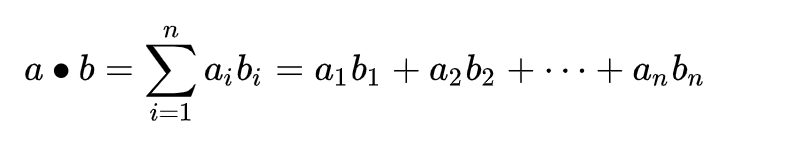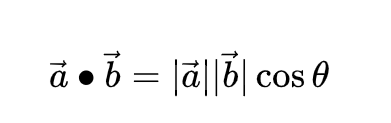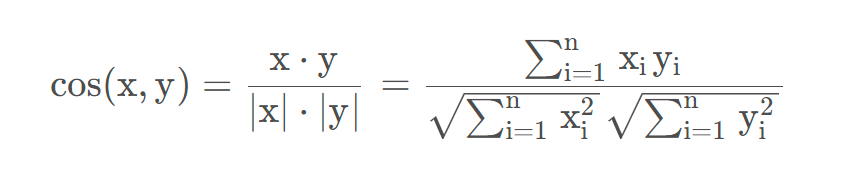R的极客理想系列文章,涵盖了R的思想,使用,工具,创新等的一系列要点,以我个人的学习和体验去诠释R的强大。
R语言作为统计学一门语言,一直在小众领域闪耀着光芒。直到大数据的爆发,R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入,R语言的社区在迅速扩大成长。现在已不仅仅是统计领域,教育,银行,电商,互联网….都在使用R语言。
要成为有理想的极客,我们不能停留在语法上,要掌握牢固的数学,概率,统计知识,同时还要有创新精神,把R语言发挥到各个领域。让我们一起动起来吧,开始R的极客理想。
关于作者:
- 张丹,分析师/程序员/Quant: R,Java,Nodejs
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/r-dot-product-similarity/
前言
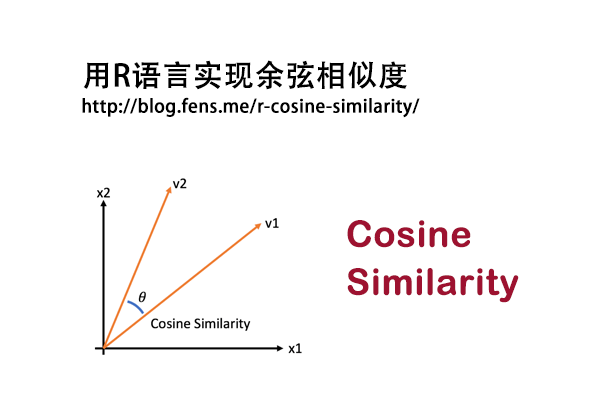
在文字处理时,我们经常需要判断两段文字是否相似,计算文本相似度有很多度种方法,文本将介绍最简单,也是计算最高效的一种方法点积相似度,与余弦相似度很像,与欧式距离相似度也很像。
目录
- 点积相似度介绍
- R语言实现点积计算
- 点积相似度应用
1. 点积相似度介绍
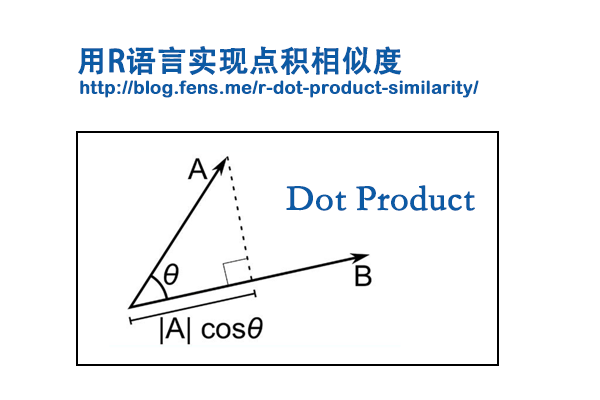
点积在数学中,又称数量积(dot product 或者 scalar product),是指接受在实数R上的两个向量并计算它们对应元素的乘机之和,也是欧几里得空间的标准内积。当两个向量进行点积操作时,结果的大小可以反映两个向量的相似性。这是因为点积操作考虑了向量的方向和大小。
点积计算
点积有两种定义方式:代数方式和几何方式。通过在欧氏空间中引入笛卡尔坐标系,向量之间的点积既可以由向量坐标的代数运算得出,也可以通过引入两个向量的长度和角度等几何概念来求解。
代数方式:
两个向量a = [a1, a2,…, an]和b = [b1, b2,…, bn]的点积定义为:
点积相似度
点积相似度,是一种计算两个向量之间相似性的方法,对于两个向量a和b,它们的点积相似度为它们对应元素的乘机之和。
假设我们有两个向量 A 和 B,它们的点积定义为:
A . B = |A| * |B| * cos(θ)
其中,|A| 和 |B| 分别是 A 和 B 的长度,θ 是 A 和 B 之间的夹角。
- 当 A 和 B 的方向相同时(即它们的夹角接近0),cos(θ) 接近 1,所以 A . B 较大。这表明 A 和 B 很相似。
- 当 A 和 B 的方向相反时(即它们的夹角接近180度),cos(θ) 接近 -1,所以 A . B 较小,甚至为负。这表明 A 和 B 不相似。
- 当 A 和 B 互相垂直时(即它们的夹角为90度),cos(θ) 为 0,所以 A . B 为 0。这表明 A 和 B 没有相似性。
因此,通过计算向量的点积,我们可以得到一个衡量两个向量相似性的标量值。在深度学习中,尤其是在自然语言处理和推荐系统中,我们经常需要衡量和比较向量(例如,单词嵌入或用户和物品的嵌入)的相似性。在这些情况下,点积是一种简单且有效的方法。
2. R语言实现点积计算
根据公式计算点积是很简单的,用R语言的基本函数,就可以完成点积的计算。
首先,定义2个向量a和b。
> a <- c(2, 5, 6)
> b <- c(4, 3, 2)
代数方式实现
> fun1<-function(a,b){
+ sum(a*b)
+ }
>
> fun1(a,b)
[1] 35
几何方式实现
> fun2<-function(a,b){
+ a %*% b
+ }
>
> fun2(a,b)
[,1]
[1,] 35
3. 点积相似度应用
接下来,我们设置一个场景,用点积相似度计算,计算不同人的简历的相似度。
假设有三个求职者A,B,C,从简历中提取了5个属性,分别是:性别、学历、籍贯、编程语言、职位。
| 姓名 | 性别 | 学历 | 籍贯 | 编程语言 | 职位 |
| A | 男 | 本科 | 浙江 | JAVA | 开发工程师 |
| B | 女 | 硕士 | 北京 | R | 算法工程师 |
| C | 男 | 本科 | 上海 | JAVA | 开发工程师 |
那么,我们可以把上面的表格转换为一个矩阵:
[
[男 本科 浙江 JAVA 开发工程师],
[女 硕士 北京 R 算法工程师],
[男 本科 上海 JAVA 开发工程师],
]
然后,我们把这个矩阵转置:
[
[男, 女, 男]
[本科, 硕士, 本科],
[浙江, 北京, 上海],
[JAVA, R, JAVA],
[开发工程师, 算法工程师, 开发工程师]
]
计算上面2个矩阵的点积,计算过程为:
[
[男 * 男 + 本科 * 本科 + 浙江 * 浙江 + JAVA * JAVA + 开发工程师*开发工程师,
男 * 女 + 本科 * 硕士 + 浙江 * 北京 + JAVA * R + 开发工程师*算法工程师,
男 * 男 + 本科 * 本科 + 浙江 * 上海 + JAVA * JAVA + 开发工程师*开发工程师],
[女 * 男 + 硕士 * 本科 + 北京 * 浙江 + R * JAVA + 算法工程师*开发工程师,
女 * 女 + 硕士 * 硕士 + 硕士 * 硕士 + R * R + 算法工程师*算法工程师,
女 * 男 + 硕士 * 本科 + 北京 * 上海 + R * JAVA + 算法工程师*开发工程师],
[男 * 男 + 本科 * 本科 + 上海 * 浙江 + JAVA * JAVA + 开发工程师*开发工程师,
男 * 女 + 本科 * 硕士 + 上海 * 北京 + JAVA * R + 开发工程师*算法工程师,
男 * 男 + 本科 * 本科 + 上海 * 上海 + JAVA * JAVA + 开发工程师*开发工程师],
]
这里为了便于计算,我们假设将值相等的点积值设为1,不相等设为0,计算结果为一个3*3的矩阵,得到计算结果为:
[
[5, 0, 4]
[0, 5, 0]
[4, 0, 5]
]
我们可以认为这个矩阵代表了,三个人之间两两的关联度,数值越大越相似。
| A | B | C | |
| A | 5 | 0 | 4 |
| B | 0 | 5 | 0 |
| C | 4 | 0 | 5 |
于是,这样我们再比较简历的时候,就可以判断谁和谁比较相似了。词向量计算,和这个计算过程是类似的。因此,在文本的的匹配过程中,每个词都可以找到与之相似度分数最高的一个关联词。
最后,我们用R语言来模拟上面的手动计算过程。
首先,用R语言来构建数据集resume。
> resume<-data.frame(
+ `姓名`=c('A','B','C'),
+ `性别`=c('男','女','男'),
+ `学历`=c('本科','硕士','本科'),
+ `籍贯`=c('浙江','北京','上海'),
+ `编程语言`=c('JAVA','R','JAVA'),
+ `职位`=c('开发工程师','算法工程师','开发工程师')
+ )
> resume
姓名 性别 学历 籍贯 编程语言 职位
1 A 男 本科 浙江 JAVA 开发工程师
2 B 女 硕士 北京 R 算法工程师
3 C 男 本科 上海 JAVA 开发工程师
把data.frame矩阵化,同时建立转置矩阵
> m1<-resume[,-1];m1
性别 学历 籍贯 编程语言 职位
1 男 本科 浙江 JAVA 开发工程师
2 女 硕士 北京 R 算法工程师
3 男 本科 上海 JAVA 开发工程师
> m2<-t(m1);m2
[,1] [,2] [,3]
性别 "男" "女" "男"
学历 "本科" "硕士" "本科"
籍贯 "浙江" "北京" "上海"
编程语言 "JAVA" "R" "JAVA"
职位 "开发工程师" "算法工程师" "开发工程师"
建立函数dot_similary(),完成点积的计算,得到点积相似度矩阵。本文的代码实现过程,没有使用矩阵的方法来实现,因此这里主要是介绍计算思路。
> dot_similary<-function(df){
+ m1<-df[,-1];m1
+ m2<-t(m1);m2
+
+ n<-nrow(m1)
+ mm<-matrix(0,nrow=n,ncol=n)
+ for(i in 1:n){
+ for(j in 1:n){
+ v<-length(which(m1[i,]==m2[,j]))
+ mm[i,j]<-v
+ }
+ }
+
+ colnames(mm)<-df[,1]
+ rownames(mm)<-df[,1] + mm + } # 运行函数,获得结果
> dot_similary(resume)
A B C
A 5 0 4
B 0 5 0
C 4 0 5
如果看看计算过程,可以打印矩阵点积计算的过程。
> row1<-paste(
+ paste(paste(m1[1,],m2[,1], sep='*'),collapse = "+"),
+ paste(paste(m1[1,],m2[,2], sep='*'),collapse = "+"),
+ paste(paste(m1[1,],m2[,3], sep='*'),collapse = "+"),
+ sep=","
+ )
> row1
[1] "男*男+本科*本科+浙江*浙江+JAVA*JAVA+开发工程师*开发工程师,男*女+本科*硕士+浙江*北京+JAVA*R+开发工程师*算法工程师,男*男+本科*本科+浙江*上海+JAVA*JAVA+开发工程师*开发工程师"
> row2<-paste(
+ paste(paste(m1[2,],m2[,1], sep='*'),collapse = "+"),
+ paste(paste(m1[2,],m2[,2], sep='*'),collapse = "+"),
+ paste(paste(m1[2,],m2[,3], sep='*'),collapse = "+"),
+ sep=","
+ )
> row2
[1] "女*男+硕士*本科+北京*浙江+R*JAVA+算法工程师*开发工程师,女*女+硕士*硕士+北京*北京+R*R+算法工程师*算法工程师,女*男+硕士*本科+北京*上海+R*JAVA+算法工程师*开发工程师"
> row3<-paste(
+ paste(paste(m1[3,],m2[,1], sep='*'),collapse = "+"),
+ paste(paste(m1[3,],m2[,2], sep='*'),collapse = "+"),
+ paste(paste(m1[3,],m2[,3], sep='*'),collapse = "+"),
+ sep=","
+ )
> row3
[1] "男*男+本科*本科+上海*浙江+JAVA*JAVA+开发工程师*开发工程师,男*女+本科*硕士+上海*北京+JAVA*R+开发工程师*算法工程师,男*男+本科*本科+上海*上海+JAVA*JAVA+开发工程师*开发工程师"
本文我们了解点积相似度的原理和实现,并且应用了点积似度,对简历中的人进行了相似度的计算,从而可以判断两个人之间的相似程度,让我们进行文本匹配时又多了一种方法。本文代码:https://github.com/bsspirit/r-string-match/blob/main/dotproduct.r
转载请注明出处:
http://blog.fens.me/r-dot-product-similarity/