用IT技术玩金融系列文章,将介绍如何使用IT技术,处理金融大数据。在互联网混迹多年,已经熟练掌握一些IT技术。单纯地在互联网做开发,总觉得使劲的方式不对。要想靠技术养活自己,就要把技术变现。通过“跨界”可以寻找新的机会,创造技术的壁垒。
金融是离钱最近的市场,也是变现的好渠道!今天就开始踏上“用IT技术玩金融”之旅!
关于作者:
- 张丹(Conan), 程序员R,Nodejs,Java
- weibo:@Conan_Z
- blog: http://blog.fens.me
- email: bsspirit@gmail.com
转载请注明出处:
http://blog.fens.me/finance-capm
前言
伴随2016年中国金融交易市场的跌宕起伏,风险越来越不确定,利率持续走低,理财等无风险资产收益持续下降的情况,唯有投资组合才能让我们的资产保值、增值。根据资本资产定价模型(CAPM),通过对金融数据的分析,构建投资组合,帮助我们在有效的市场中控制风险、稳定收益。
本文将深入浅出地介绍资本资产定价模型,从理论到建模,再到程序现实。资本资产定价模型反应的是资产的风险与期望收益之间的关系,风险越高,收益越高。当风险一样时,投资者会选择预期收益最高的资产;而预期收益一样时,投资者会选择风险最低的资产。
由于本文为非金融教材类文章,所以当出现与教课书不符的描述,请以教课书为准。本文力求用简化的语言,来介绍自资本资产定价模型的知识,同时配合R语言的实现。
目录
- 故事背景
- 资本市场线
- 资本资产定价模型
- 用R构建投资组合模型
- Beta VS Alpha
1. 故事背景
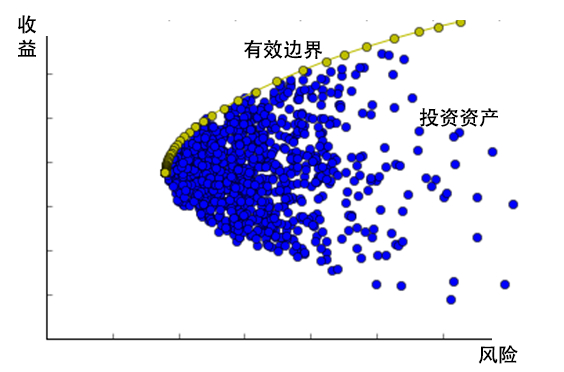
1952年,马科维茨(Markowitz)提出了投资组合选择理论,他认为最佳投资组合应当是,风险厌恶特征的投资者的无差异曲线和资产的有效边界线的交点。投资者在选择资产时会在收益和风险之间做出平衡:当风险一样时,会选择预期收益最高的资产;而预期收益一样时,会选择风险最低的资产。
图1 投资组合选择示意图
到1964年,威廉-夏普(William Sharp),约翰-林特纳(John Lintner)与简-莫森(Jan Mossin)则在马科维茨基础上提出的单指数模型,将市场组合引入均值-方差模型,极大地简化了计算,他们认为获得了市场任意资组合的收益与某个共同因素之间是有线性关系,最终将其发展为资本资产定价模型(Capital Asset Pricing Model, CAPM)。从马科维茨的投资组合选择理论,发展到资本资产定价模型经历了一个漫长的过程。
简单一句话概括,资本资产定价模型的核心思想,资产价格取决于其获得的风险价格补偿。
假设条件
资本资产定价模型,是基于一系列假设条件而成立的。但这些条件,可能并不符合现实的标准,资本资产定价模型也一度遭到质疑。
- 资产可以无限分割。
- 不存在交易成本和个人所得税。
- 可以无限卖空。
- 存在一种无风险利率,投资者在此利率水平下,可以无限制地贷出和借入任意数额的资金。
- 投资者是价格接受者,市场是完全竞争的。
- 投资者是理智的,通过比较资产的期望收益和方差来作出投资决策,在相同预期收益下会选择风险最小的资产。
- 投资者在相同的投资期限出作出决策,而市场信息是公开免费的,并可以及时获得。
- 投资者对市场中的经济变量有相同的预期,他们对任意资产的预期收益率、市场风险的看法是一致的。
资本资产定价模型的核心假设是认为市场满足完全、无摩擦和信息完会对称的条件,市场中的投资人都是Markowitz理论中的理性经济人。
2. 资本市场线
由于涉及到金融专业领域,有几个概念是我们应该提前知道的。
- 风险资产:风险资产是指具有未来收益能力的资产,但收益率不确定且可能招致损失,比如股票、债券等。
- 无风险资产:没有任何风险或者风险非常小的资产,有确定的收益率,并且不存在违约的风险。
- 收益率:指从投资开始到投资结束时,所获得的投资回报率。
- 无风险收益率:无风险资产,所产生的投资回报率。
- 投资组合:由投资人或金融机构所持有的股票、债券、基金、衍生金融产品等组成的集合,目的在于分散风险。
- 杠杆交易:就是利用小资金来进行数倍于原始金额的投资,以期望获取相对投资标的物波动的数倍收益率的盈利或亏损。
2.1 风险资产
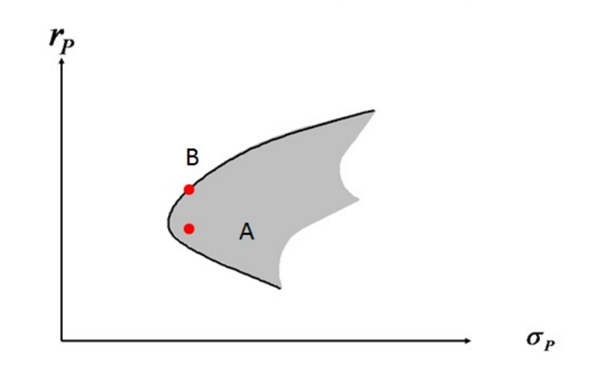
对于风险资产来说,我们可以用预期收益和风险,通过二维的坐标来进行描述。
对上图的解释:
- X轴,为风险
- y轴,为收益率
- 灰色区域,为金融资产可投资区域
- 黑色线,为有效投资边界
- A和B点,为2个风险资产
A和B有相同的x值,表示具有相同的风险。B点在A点上面,表示B的收益率高于A。对于理性的投资者来说,如果只在A点和B点之间做投资选择,那么大家都会投资到B点,而不投资于A点。
2.2 无风险资产
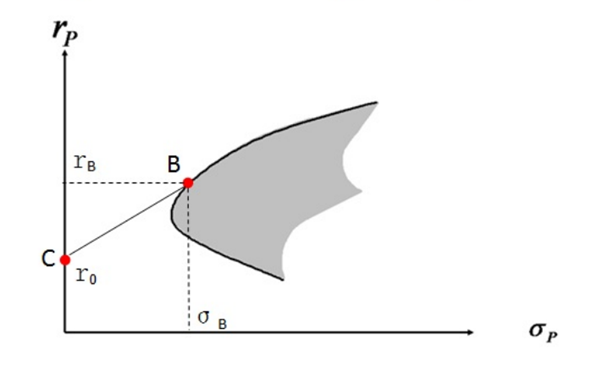
在下图中,我们加入无风险资产,来比较无风险资产和风险资产的关系。
对上图的解释:
- B点,为1个风险资产,在有效投资边界上
- C点,为无风险资产,在y轴上
- X轴,为风险
- y轴,为收益率
- 灰色区域,金融资产为可投资区域
- 黑色线,为有效投资边界
C点为无风险资产,他的位置在图示的y轴上,这时x为0,即风险为0。我们可以把投资,分配到C点或B点上。如果都投到C点,那么我们将获得的是R0部分的无风险收益;如果都投到B点,那么我们需要承担σB的风险,同时获得RB的风险收益。如果我们把资金,一部分投资到B点对应的风险资产上,另一部分投资到C点对应的无风险资产上,那么将构成一个由B和C资产组成的投资组合,而且风险和收益部分,将体现在B和C的连线上。
2.3 最优组合
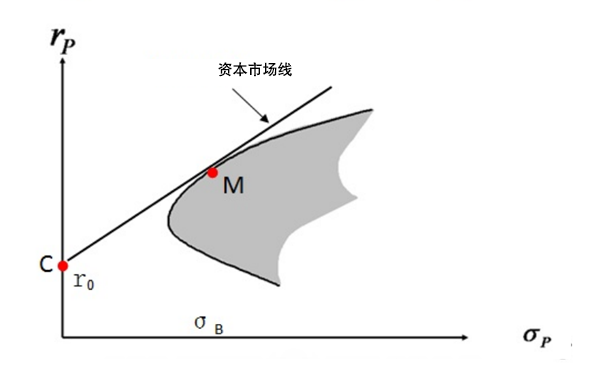
那么,有没有最优的投资组合呢?收益最大、风险最小。下面就让我们来,发现这个最优的组合M。
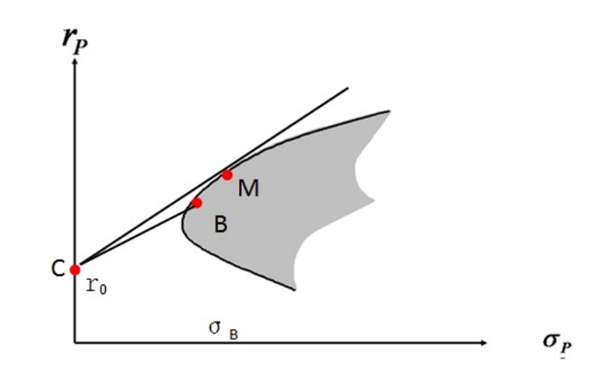
对上图的解释:
- M点,为最优组合的风险资产
- B点,为1个风险资产,在有效投资边界上
- C点,为无风险资产,在y轴上
- X轴,为风险
- y轴,为收益率
- 灰色区域,金融资产为可投资区域
- 黑色线,为有效投资边界
假设有最优的组合,在上图中M点处,当我们把C和M进行连线,使得CM的连线与灰色区域相切。从图上看,CM的连线会比任意的C与可投资区域点的连线斜率都要大,比如C和B的连线。我们取CB的连线的延长线,在CB的延长线上找到,与M具有相同x的点B’,这时M与B’风险相同,M点在B’点的上面,所以M点的收益率大。也就是说,当风险相同的时候,我们都会选择收益率最大的资产。
不论从可投资区域中怎么选取,M点都是斜率最大的点,那么我们可以认为,M点为市场上各资产的最优的投资组合.
对于最优的投资组合,其实不管投资者的收益风险的偏好是什么样子的,只要找到了最优的风险资产组合,再加上无风险的资产,就可以为投资者获得最佳的投资方案了。那么对于理性的投资者,如果发现了最优的组合,他们只会投资于这个组合,这时与收益和风险偏好无关。
M点构建的投资组合,一般是由所有可投资证券产品组成的,每种证券资产构成的比例,为证券的相对市值。无风险资产C,并没有包括在M中,人们都会选择CM的连接线进行投资,来构建最优的投资组合。
在实际的市场交易中,金融资产的价格会发生偏离,因为价格受市场的供需关系所影响,当价格发生偏离后,市场会自动修复会回均衡价格水平。
2.4 资本市场线
对于CM的连线,就是马科维茨提出了投资组合选择理论,风险厌恶特征的投资者的无差异曲线和资产的有效边界线的交点。这条线就叫,资本市场线(Capital Market Line)。
资本市场线是指表明有效组合的期望收益率和标准差之间的一种简单的线性关系。
资本市场线决定了证券的价格。因为资本市场线是证券有效组合条件下的风险与收益的均衡,如果脱离了这一均衡,则就会在资本市场线之外,形成另一种风险与收益的对应关系。
2.5 投资组合构建
资本市场线,就是我们最优的投资组合,当我们发现这个投资组合,所有资金都会投到这个组合上。通过对无风险资产C和风险资产M分配不同的投资权重,我们可以自己配置出自己想要的风险和收益来,同时可以利用金融工具来加杠杆放大风险和收益的范围。
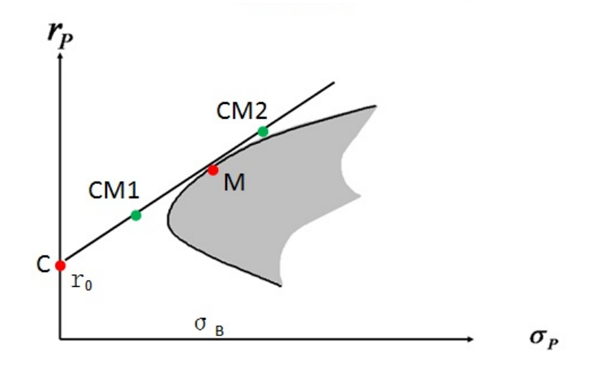
如果我们把投资者分成,风险厌恶型和风险激进型。
对于风险厌恶型,他们对于资金安全有非常高的要求,不追求高收益但求本金安全,这些资金通常都是用来生活的。那么在为这些资金做资产配置方案的时候,可以把一部分资金配置无风险资产上,同时少量资金配置到M点的最优组合上,保证低风险并获得少量收益。
如图中CM1点,如果配置50%的风险资产M和50%的无风险资产C,来实现投资组合。公式如下:
CM1 = 0.5C + 0.5M对于风险激进型,他们对于资金有非常高的收益要求,本金可以部分或全部损失,这些资金通常都是“闲钱”,就是用来进行投资活动的。那么在为这些资金做资配置方案时,可以全部都投到M上,再激进点,可以通过借钱、融资的方式,增加杠杆,把资金放大进行投资。这种操作风险会随着杠杆的放大剧增,当然同时你也会有更大的收益。
如图中CM2点,落在了CM的延长线上。我们可以配置150%的风险资产M,同时用50%的钱去抵押以无风险资产C的收益率去借钱。公式如下:
CM2 = -0.5C + 1.5M2.6 风险和收益的关系
上面我们描述风险和收益的关系,主要是从思路上定性介绍,没有进行定量描述,那么究竟风险和收益从数学上怎么进行定义呢。
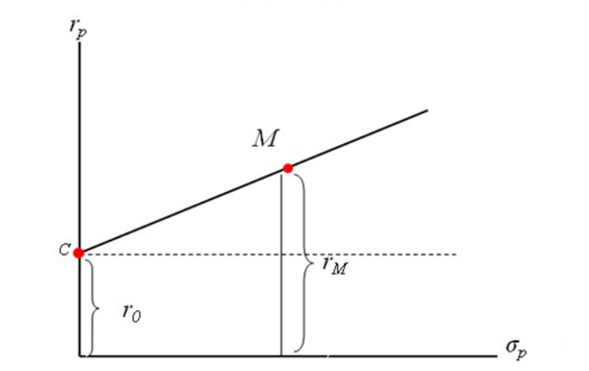
对上图的解释:
- M点,为最优组合的风险资产
- C点,为无风险资产,在y轴上
- r0,为无风险资产的收益率
- rM,为M点的收益率
- x轴,σp为风险资产的收益率的方差
- y轴,rp为收益率
根据威廉-夏普所引入的均值-方差模型,极大地简化了计算,就是解决了公式计算的问题。用方差来刻画风险,建立收益和风险的一元线性关系。可以用下面公式来表示:
公式
E(rm) – r0 = A * σM^2公式解释:
- E(rm):市场投资组合的预期收益率
- r0:无风险收益率
- E(rm)–r0, 市场投资组合的风险溢价
- σM^2: 市场投资组合方差Var(rM)
- A:风险厌恶水平
有了公式,我们就明确的知道了,风险和收益的定量关系,并且可以利用数据来进行计算。
3. 资本资产定价模型
对于市场的投资组合,风险溢价和市场投资组合的方差成线性关系。但对于单个资产来说,收益和风险是市场投资组合组成的一分部,受市场共同变化的影响。
3.1 单个资产风险溢价
对于单个资产的风险来说,在资本资产定价模型中,用β来进行表示。β是衡量单个金融资产与市场收益的共同变化程度,通过协方差来计算。单个资产的风险为,当前资产与投资组合收益率的协议差,除以投资组合收益率的方差。
单个资产的风险的计算公式:
βi = Cov(ri, rm) / Var(rm)
= Cov(ri, rm) / σm^2
单个资产的风险溢价的计算公式:
E(ri) – rf = (Cov(ri, rm) / σm^2)*[E(rm) – rf]
= βi * [E(rm) – rf]
对公式的解释:
- E(ri),为风险资产i的预期收益
- E(rm),为市场投资组合的预期收益
- rf,为无风险资产收益
- Cov(ri, rm),为风险资产收益率和市场投资组合收益率的协议差
- Var(rm),为市场投资组合的收益率的方差
从公式可以看出,单个资产的风险溢价与市场投资组合M的风险溢价成正比,受β影响。
3.2 资本资产定价模型
资本资产定价模型,是现化金融学中的基石理论。在上述假设条件下,可以推到出资本资产定价模型的具体公式。整个和推到过程,就是上面文章介绍的过程,从后人学习的角度看,这个理论比较简单的,仅用到了简单地统计学知识,但是前人却花了很长的时间研究和探索。
判断单个资产的风险时,当β=1时,则说明当前资产与整个市场的趋势是完全保持一致的;当β为2时,代表高风险,其回报的变化将大于市场大盘的变化幅度;当β为0.5时,代表是低风险的资产配置。
3.3 2种风险
在资本资产定价模型,定义了2种风险,即系统性风险和非系统性风险。
系统性风险,就是由外部因素引起的风险,比如:通货膨胀,GDP,重大政治事件等等。这一类事件对于资产收益率的影响不能通过组合本身来消除的,所以这一类风险对于投资者来说是无法回避的。
非系统性风险,就是组合内部结构引起的风险,比如:A股与B股高度相关,A股的收益率出现大幅波动的时候,B股也会出现相似幅度的波动,波峰叠加或波谷叠加,就会增加整个组合的风险;反之,如果A与B为负相关,则A与B的波动就会相互抵消。这样,风险是由组合里的资产类型决定的,所以通过多样化分散的投资策略,无论在理论还是实际上,这种风险都是可以最小化甚至消除的。而这个消除的过程中,整个投资组合的收益率是不会下降的。
3.4 2种收益
与风险相对应是收益,我们承受了2种风险的同时,也获得了风险所带来的收益。一部分是与市场完全相关收益部分,即beta(β)收益;另一部分与市场不相关的收益部分,即alpha(α)收益。
- beta收益,相对容易获得,例如,你看好一个市场,可以持有成本低廉的对应市场的指数基金,等待市场上涨。
- alpha收益,比较难获得,alpha是体现投资水平的策略收益。
alpha是,投资组合的实际期望收益与预期收益之间的差。计算alpha的公式为:
E(ri) – rf = αi + βi * [E(rm) – rf]
αi = [E(ri) – rf] - βi * [E(rm) – rf]
alpha是衡量投资人投资水平的,我们举个例来说明。比如:市场收益率为14%,A证券的β=1.2,短期国债利率6%,投资者对这只股票的进行了交易,获得的实际收益为17%,那么我们怎么判断投资人的水平呢?
首先,先求出A证券的预期收益率 = 6% + 1.2*(14-6)% = 15.6%,再用投资者实际收益减去A证券预期收益 17% – 15.6% = 1.4%。最后获得的1.4%就是alpha,表示投资者能力,可以额外获得1.4%的收益。
3.5 资本资产定价模型的应用场景
进行组合投资分散风险:投资者可以按市场组合的构成比例分散持有多种风险资产,使持有的风险资产组合最大限度地接近市场组合,以达到消除非系统风险的目的。
调整收益风险比例:将无风险资产与风险资产市场组合进行再组合,以获得所希望的个性化的风险收益组合。
指数化投资:将资产配置在与某一指数相同的权重的投资方法,通过微调权重或成分,获得比指数更好的alpha。
资产定价:资本资产定价模型可以用来判断有价证券或其他金融资产的市场价格是否处于均衡水平,是否被高估或低估,以便通过套利活动获取超额收益。
基金购买:举一个贴近市场的例子,当我们要购买基金时,也可以用到资本资产定价模型帮我们分析。比如,基金A的期望收益率12%,风险β=1,基金B期望收益率13%,β=1.5。市场期望收益率11%,无风险资产收益率r0 = 5%。 那么哪只基金更值得买?
当你每天打开支付宝,看到里面的各种基金推荐。你就会发现这是一个实际的问题。如果你懂学了本文,按照资本资产定价模型的思路,其实就是求alpha,哪个基金的alpha高,就买哪个。
求alpha,我们就直接套用公式。
αA = 12 – 5 – 1 * [11 - 5] = 1%
αB = 13 – 5 – 1.5* [11 -5 ] = -1%
基金A的alpha为1%,而基金B的alpha为-1%。结论就很明显,基金A的管理人能力很好,超额收益1%;而基金B的管理人,就差一些,盈利低于市场1%。所以,我们会投资基金A,而不会投资基金B。
4. 用R构建投资组合模型
花了大量的篇幅介绍了资本资产定价模型的原理,对于程序实现其实是相当简单地。因为R语言中,已经把资本资产定价模型相关的计算函数都封包好了,我们仅仅是调用就能完成整个的计算过程。
R语言程序实现,我们主要会用到2个包,quantmod和PerformanceAnalytics。对于为什么要用R语言,可以参考文章R语言为量化而生
- quantmod,用于下载数据。
- PerformanceAnalytics,用于进行各种评价指标计算。
我们设计一个应用场景,假如我有10万美金想投资于美国的股市,我想获得比标普好(SP500)的投资收益,那么我应该如何购买股票。
首先,我们先想清楚,我的最终的目标是“比标普好的投资收益”。其次,我们基于资本资产定价模型理论基础,从投资组合角度思考投资策略,而不是技术指标的角度。比标普好,那么我们就需要以标普指数做为理想投资组合。然后,我们去市场上选择几个股票,分别计算出收益率,beta,alpha等指标,判断是否符合的预期,反复测试,直到找到合适的股票或股票组合。
本文只是案例介绍,用于说明投资思路和方法,不购成任何的股票推荐。
本文的系统环境
- Win10 64bit
- R version 3.2.3 (2015-12-10)
从yahoo下载IBM,GE(通用电器),YHOO(Yahoo)的3只股票,从2010年01月01日的日行情数据,同时下载标普指数(SP500)的日行情数据。
下面代码并不完整,但思路已经给出,请大家不要太随意地张嘴要数据和代码,毕竟写一篇文章非常辛苦。如果你想直接用我的代码,请扫文章下面二维码,请作者喝杯咖啡吧。 :_D
执行R语言程序。
# 加载程序包
> library(quantmod)
> library(PerformanceAnalytics)
# 从yahoo下载3只股票的数据,和SP500的数据
> getSymbols(c('IBM','GE','YHOO','^GSPC'), from = '2010-01-01')
# 打印前6行和后6行数据
> head(GSPC)
open high low close volume adjusted
2010-01-04 1116.56 1133.87 1116.56 1132.99 3991400000 1132.99
2010-01-05 1132.66 1136.63 1129.66 1136.52 2491020000 1136.52
2010-01-06 1135.71 1139.19 1133.95 1137.14 4972660000 1137.14
2010-01-07 1136.27 1142.46 1131.32 1141.69 5270680000 1141.69
2010-01-08 1140.52 1145.39 1136.22 1144.98 4389590000 1144.98
2010-01-11 1145.96 1149.74 1142.02 1146.98 4255780000 1146.98
> tail(GSPC)
open high low close volume adjusted
2016-12-20 2266.50 2272.56 2266.14 2270.76 3298780000 2270.76
2016-12-21 2270.54 2271.23 2265.15 2265.18 2852230000 2265.18
2016-12-22 2262.93 2263.18 2256.08 2260.96 2876320000 2260.96
2016-12-23 2260.25 2263.79 2258.84 2263.79 2020550000 2263.79
2016-12-27 2266.23 2273.82 2266.15 2268.88 1987080000 2268.88
2016-12-28 2270.23 2271.31 2249.11 2249.92 2392360000 2249.92
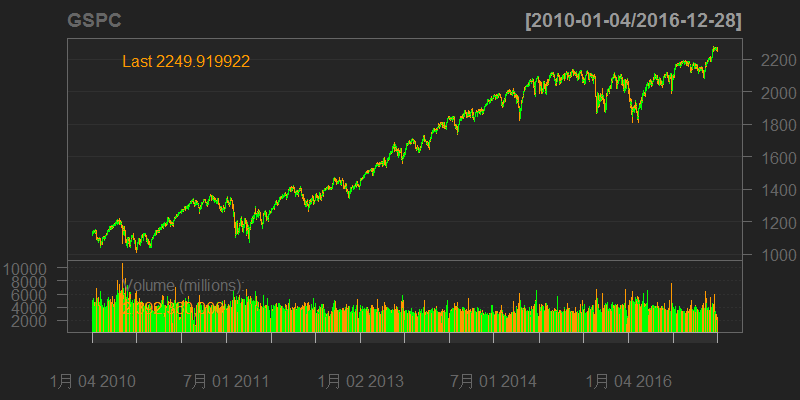
# 画出SP500的K线图
> barChart(GSPC)
把4个品种的调整后的价格进行合并。
> # 改列名
> names(IBM)<-c("open","high","low","close","volume","adjusted")
> names(GE)<-c("open","high","low","close","volume","adjusted")
> names(YHOO)<-c("open","high","low","close","volume","adjusted")
> names(GSPC)<-c("open","high","low","close","volume","adjusted")
# 数据合并
> dat=merge(IBM$adjusted,GE$adjusted,YHOO$adjusted,GSPC$adjusted)
> names(dat)<-c('IBM','GE','YHOO','SP500')
# 打印前6行
> head(dat)
IBM GE YHOO SP500
2010-01-04 112.2859 12.27367 17.10 1132.99
2010-01-05 110.9295 12.33722 17.23 1136.52
2010-01-06 110.2089 12.27367 17.17 1137.14
2010-01-07 109.8274 12.90920 16.70 1141.69
2010-01-08 110.9295 13.18724 16.70 1144.98
2010-01-11 109.7680 13.31435 16.74 1146.98
计算每日收益率,合并收益率到dat_ret
> dat_ret=merge(IBM_ret,GE_ret,YHOO_ret,SP500_ret)
> names(dat_ret)<-c('IBM','GE','YHOO','SP500')
> head(dat_ret)
IBM GE YHOO SP500
2010-01-04 0.009681385 0.015111695 0.009445041 0.0147147759
2010-01-05 -0.012079963 0.005177994 0.007602339 0.0031156762
2010-01-06 -0.006496033 -0.005151320 -0.003482298 0.0005455205
2010-01-07 -0.003461515 0.051779935 -0.027373267 0.0040012012
2010-01-08 0.010034759 0.021538462 0.000000000 0.0028817272
2010-01-11 -0.010470080 0.009638554 0.002395150 0.0017467554
定义无风险收益率为4%,计算4个资产的平均年化收益率。
# 无风险收益率
> Rf<-.04/12
# 计算平均年化收益率,平均年化标准差,平均年化Sharpe
> results<-table.AnnualizedReturns(dat_ret,Rf=Rf)
> results
IBM GE YHOO SP500
Annualized Return 0.0345 0.1108 0.1257 0.1055
Annualized Std Dev 0.1918 0.2180 0.3043 0.1555
Annualized Sharpe (Rf=84%) -2.8892 -2.3899 -1.6911 -3.3659
统计指标分析,每个资产有1760个样本点,没有NA值。日最小收益率,YHOO最小为-0.0871。日最大收益率,在GE为0.1080。算数平均,几何平均,方差,标准差都是YHOO最大。
# 计算统计指标
> stats
IBM GE YHOO SP500
Observations 1760.0000 1760.0000 1760.0000 1760.0000
NAs 0.0000 0.0000 0.0000 0.0000
Minimum -0.0828 -0.0654 -0.0871 -0.0666
Quartile 1 -0.0060 -0.0065 -0.0098 -0.0039
Median 0.0002 0.0004 0.0005 0.0005
Arithmetic Mean 0.0002 0.0005 0.0007 0.0004
Geometric Mean 0.0001 0.0004 0.0005 0.0004
Quartile 3 0.0067 0.0077 0.0112 0.0053
Maximum 0.0567 0.1080 0.1034 0.0474
SE Mean 0.0003 0.0003 0.0005 0.0002
LCL Mean (0.95) -0.0004 -0.0001 -0.0002 0.0000
UCL Mean (0.95) 0.0008 0.0012 0.0015 0.0009
Variance 0.0001 0.0002 0.0004 0.0001
Stdev 0.0121 0.0137 0.0192 0.0098
Skewness -0.5876 0.3084 0.0959 -0.3514
Kurtosis 4.6634 4.7294 2.9990 4.0151
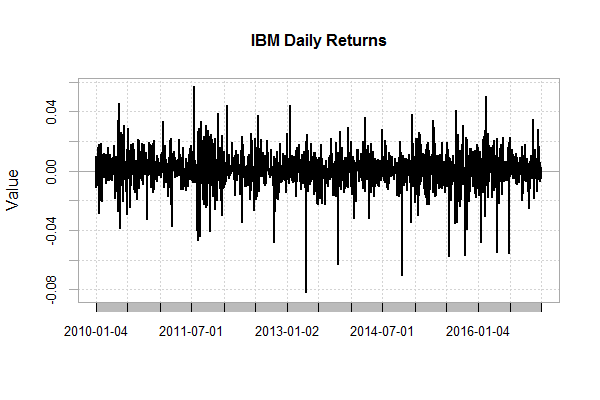
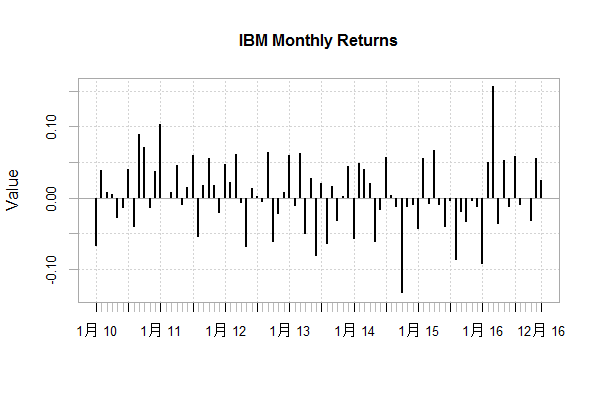
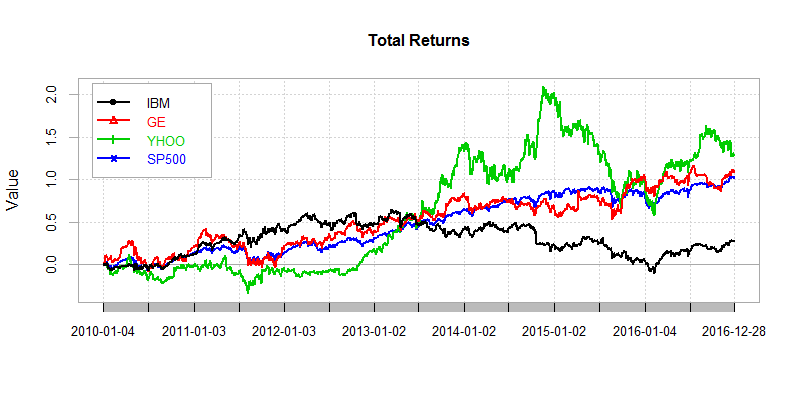
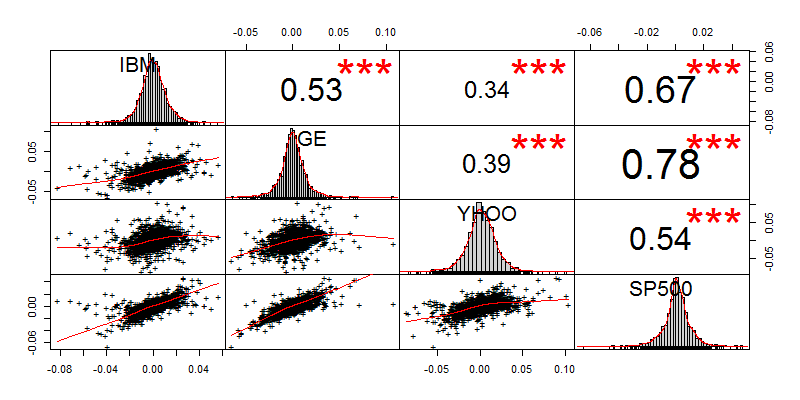
画出IBM股票,日收益和月收益的图,4个资的累积收益率图,并对4个资产做相关性分析。
从上图中可以看出,红线(GE)和蓝线(SP500)的走势基本稳合,说明GE在从2010开始在跟着美国经济持续发展。绿线(YHOO)从2013初到2015年初大幅拉升,领先于SP500很多,说明这段时期YHOO所处的互联网行业,带来了非常大的市场红利;从2015年到2016年,又下跌很大,大起大落,受市场影响非常敏感。黑线(IBM)大部分时间都处于SP500的下方,说明美国经济这几年的高速发展,并没有给IBM带来很大的发展空间。如果从我们的目标来说,”比标普好的投资收益”那么我们只能选择GE或YHOO。
对4个品种进行相关性分析,发现GE和SP500相关系数为0.78,是3只股票中最相关的。而YHOO是与其他3个品种走势最不一样的。
最后,以SP500为市场组合,分别计算出3只股票的alpha和beta。
# 计算alpha
> CAPM.alpha(dat_ret[,1:3],dat_ret[,4],Rf=Rf)
IBM GE YHOO
Alpha: SP500 -0.000752943 0.0003502332 0.0003944279
# 计算beta
> CAPM.beta(dat_ret[,1:3],dat_ret[,4],Rf=Rf)
IBM GE YHOO
Beta: SP500 0.8218135 1.098877 1.064844
3只股票中,IBM的alpha是最小的,而且是负的,说明IBM落后于市场,买IBM不如直接SP500更好。GE的Beta是最大的,在上升时期beta越大,获得的市场收益也会越大。YHOO从Alpha和Beta上看,虽然与GE接近,但由于标准差,最大回撤等指标过大,会导致波动太大。
综上分析,我们如果配置部分GE和部分YHOO,就可以获得比标普好的收益,但由于GE和YHOO的beta都高于SP500,所以风险也会高于SP500,需要增加新的股票来分散风险,具体的定量分析,将在以后的文章中再进行介绍了。
5. Beta VS Alpha
最后,补充一些Alpha和Beta的说明。Alpha和Beta的认知最早是一个股市起源的概念,是一个关于投资组合的收益率分解的问题
- Alpha:一般被认为是投资组合的超额收益,也既管理人的能力;
- Beta:市场风险,最初主要指股票市场的系统性风险
Alpha是平均实际回报和平均预期回报的差额。
- α>0,表示一基金或股票的价格可能被低估,建议买入。
- α<0,表示一基金或股票的价格可能被高估,建议卖空。
- α=0,表示一基金或股票的价格准确反映其内在价值,未被高估也未被低估。
Beta反映了单个证券与整体市场组合的联动性。
- β>1,攻击性,市场上升时涨幅大。
- β<1,防御性,市场下跌时跌幅小。
- β=1,中立性,与市场波动一致。
从资本资产定价模型开始发展到现今,已经有很长的时间了。金融理论在一直发展,继资本资产定价模型之后又一重要的理论突破是套利定价理论,我将在下一篇文章中进行介绍。
本文中,我详细地介绍了资本资产定价模型的金融理论、推到过程、以及R语言实现,用我自己的理解进行阐述。希望能给走在量化道路上的朋友带来入门的指引和帮助,也希望找到像我一样,通过IT转金融的人,让我一起用IT技术+金融的思维在金融市场抢钱吧。
转载请注明出处:
http://blog.fens.me/finance-capm