• Posts tagged "均线"

Blog Archives

Posted:
Jul 26, 2015
Tags:
Comments:
17 Comments

均值回归，逆市中的投资机会

用IT技术玩金融系列文章，将介绍如何使用IT技术，处理金融大数据。在互联网混迹多年，已经熟练掌握一些IT技术。单纯地在互联网做开发，总觉得使劲的方式不对。要想靠技术养活自己，就要把技术变现。通过“跨界”可以寻找新的机会，创造技术的壁垒。

金融是离钱最近的市场，也是变现的好渠道！今天就开始踏上“用IT技术玩金融”之旅！

关于作者：

  • 张丹(Conan), 程序员Java,R,PHP,Javascript
  • weibo：@Conan_Z
  • blog: http://blog.fens.me
  • email: bsspirit@gmail.com

转载请注明出处：
http://blog.fens.me/finance-mean-reversion/

meanReversion

前言

在股票市场中有两种典型的投资策略：趋势追踪(Trend Following) 和 均值回归(Mean Reversion)。 趋势追踪策略的特点在大行情的波动段找到有效的交易信号，不仅简单而且有效，我之前写的一篇文章 两条均线打天下 就属于趋势追踪策略。而均值回归策略则是一种反趋势策略，一波大幅上涨后容易出现下跌，而一波大幅下跌后容易出现上涨。其特点在振荡的在震荡的市场中非常有效，捕捉小的机会，本文就将介绍这种策略。

目录

  1. 均值回归原理
  2. 均值回归模型和实现
  3. 量化选股

1. 均值回归原理

在金融学中，均值回归是价格偏离均衡价格水平一定程度后向均衡价格靠拢的规律。本质上，均值回归就是哲学思想中所说的物极必反，可以简单地概括为“涨多必跌，跌多必涨”的规律。

均值回归是指股票价格无论高于或低于均值(均衡价格水平)都会以很高的概率向均值回归。根据这个理论，股票价格总是围绕其均值上下波动。一种上涨或者下跌的趋势不管其延续的时间多长都不能永远持续下去，最终均值回归的规律一定会出现：涨得太多了，就会向均值移动下跌；跌得太多了，就会向均值移动上升。如果我们认为事物总要回归常态，并且基于这样的预期来做任何决策的时候，我们就是在应用均值回归的理论。

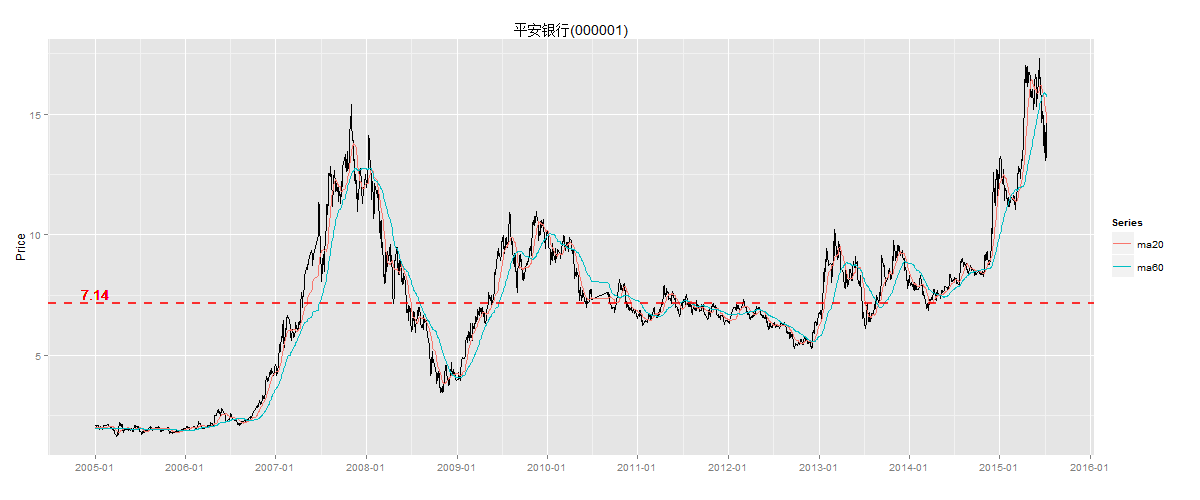
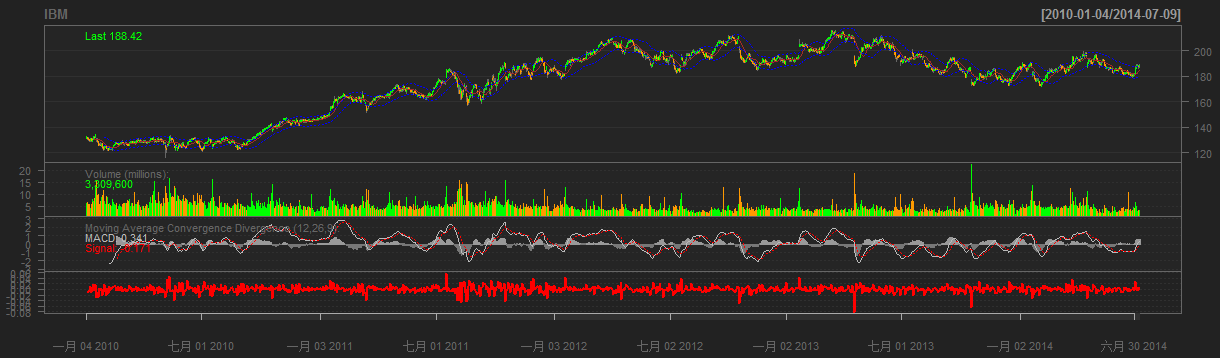
下面以平安银行(000001)股票日K线图为例，可以非常直观的了解均值回归这种现象， 截取2005年到2015年7月的股票数据，股价为向前复权的价格。

01

上图中有3条曲线，黑色线是平安银行向前复权后的每日股价，红色线为20日均线，蓝色线为60日均线。关于均线的介绍，请参考文章 两条均线打天下。图中还有一条红色的水平线虚线，是这10年的股价平均值等于7.14元。这10年间，平安银行的股价经历了几波上涨和下跌，多次穿越7.14平均值。那么这个现象就是我们要讨论的均值回归。

1.1 均值回归的3个特性

均值回归是价值投资理论成立的一个核心理论，具有3个特性：必然性、不对称性、政府调控。

必然性，股票价格不能总是上涨或下跌，一种趋势不管其持续的时间多长都不能永远持续下去。在一个趋势内，股票价格呈持续上升或下降，我们称之为均值回避(Mean Aversion)。当出现相反趋势时就呈均值回归(Mean Reversion)，但回归的周期有随机性是我们不能预测。不同的股票市场，回归的周期会不一样的，就算是相同的市场，回归的周期也是不一样的。

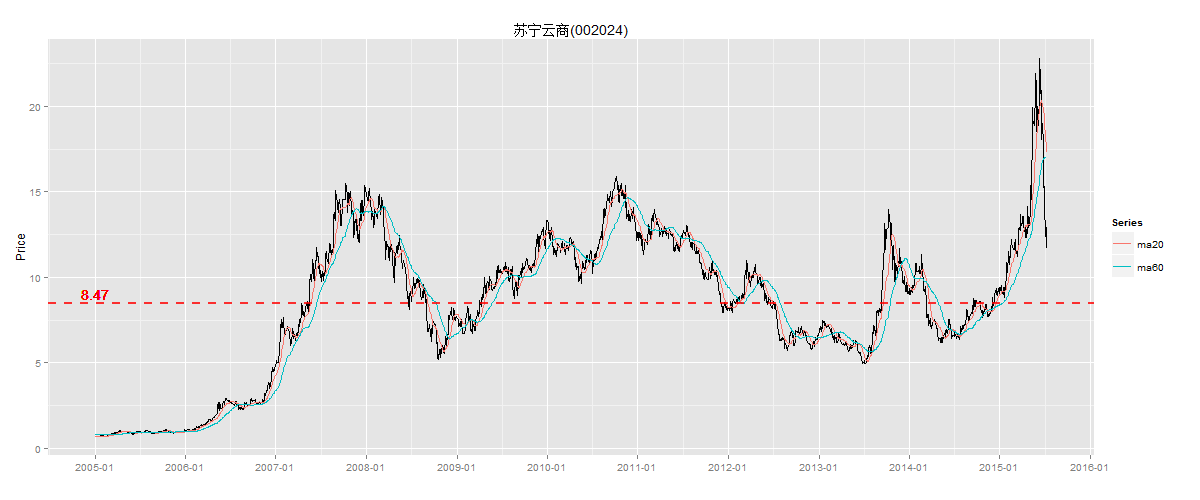
我们换支股票，以苏宁云商(002024)股票日K线图为例, 同样截取2005年到2015年7月的向前复权的股价数据，如下图所示。我们看到苏宁云商在2006年到2007年有一波大涨随后下跌；从2009到2010年时，第二波大涨；2013年下半年迎来第三波大涨；2014年下半年到2015年第四波大涨。从图形上可以直观看到，2015年这波涨的最急，波动率也是最大的；从现象中，我们可以判断一种趋势不管其持续的时间多长都不能永远持续下去。

02

不对称性，股价波动的幅度与速度是不一样的，回归时的幅度与速度具有随机性。对称的均值回归才是不正常的、偶然的，这一点也也可以从股票中所验证。

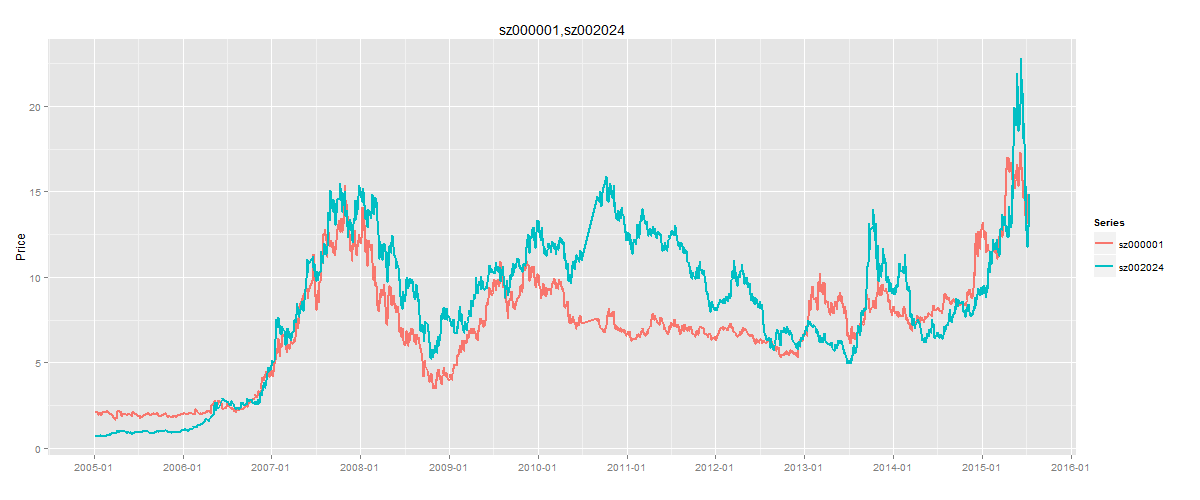
我们合并平安银行(000001)和苏宁云商(002024)股票日K线图为例,所下图所示。两支股票在2007年中，都赶上了大的上涨行情，曲线基本吻合。到2008年2支股票都遇到了大跌，但波动率和速度都是不一样的，随后在2010年到2012年出现了完成不一样的走势，无规律可寻，体现了均值回归时的随机性和不对称性。

03

政府行为，股票收益率不会偏离价值均值时间太久，市场的内在力量会促使其向内在价值回归。市场在没有政府政策的作用下，股票价格会在市场机制下自然地向均值回归。但这并不否定政府行为对促进市场有效性的作用，因为市场偏离内在价值后并不等于立即就会向内在价值回归，很可能会出现持续地均值回避。政府行为会起到抑制市场调节市场的作用，是必不可少的因素之一，市场失灵也是政府参与调控的直接的结果。

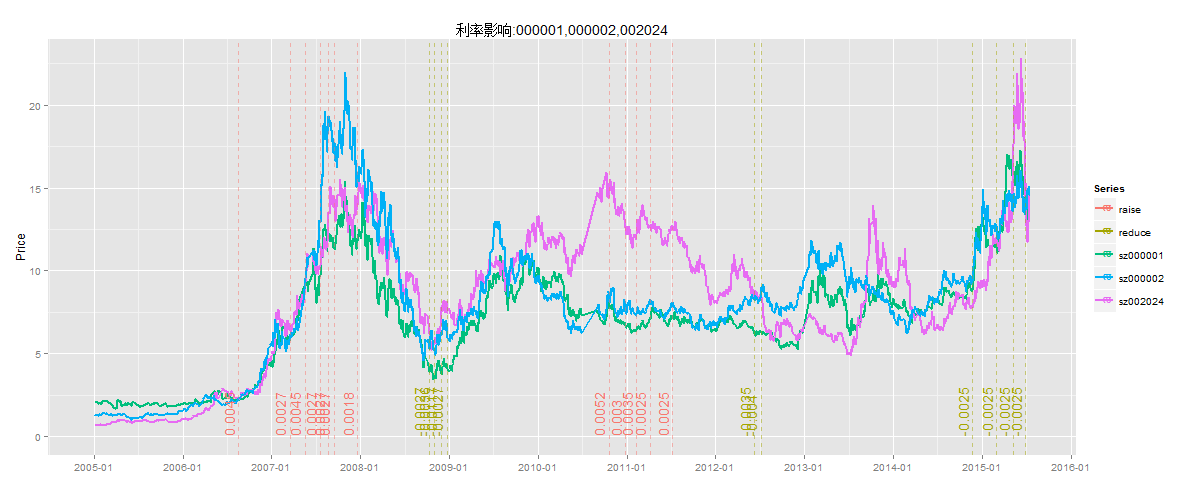
对于政府政策行为，比如升准、降准、升息、降息，在股市中都会有比如明显的体现。房地产股、银行股，都会受到国家宏观调控的直接的影响。下如所示，在图中增加万科A(0000002)的股票，图中3条线分别是平安银行，万科A，苏宁云商3支股票。我们发现地产和银行的股价走势是比较相近的，而电商的走势是不太一样的。

另外，增加2种颜色的辅助线，红色为升息的时间点和利率变动值，黄色为降息的时间点和利率变动值。当2007年股市超涨的时候，国家宏观调控通过升息鼓励存款，抑制高股价；当股票超跌的时候，通过降息推动投资和消费。2015年金融改革，政府一直都在降息拉动股市。从图中，我们看到万科A和平安银行对于升息和降息的调控是比较明显的，对于苏宁云商就不是特别的明显了。

04

通过对市场的回顾，我们基本验证了均值回归的理论是和市场的行为是一致的。那么，接下来我们应该如何应用这个理论来找到投资的切入点呢？

1.2 计算原理和公式

从价值投资的角度，我们发现股价会在平均值上下波动，但如果考虑到资金的时间成本，把钱都压在股市中，等待几年的大行情，也是很不划算的。那么我们就需要对价值均值进行重新定义，以20日均值来代替长期均值，找到短周期的一种投资方法。

计算原理：取日K线，以N日均线做为均值回归的短期均衡价格水平(均值)，计算股价到均值的差值，求出差值的N日的平均标准差，从而判断差值的对于均值的偏离，当偏离超过2倍标准差时，我们就认为股价超涨或超跌，股价会遵循均值回归的理论，向均值不停地进行修复。

计算公式:


N日平均值     =  [T日股价 + (T-1)日股价 + ... + (T-(N-1))日股价]/N
差值          =  N日平均值 - N日股价
N日差值均值   =  [T日差值 + (T-1)日差值 + ... + (T-(N-1))日差值]/N
N日差值标准差 =  sqrt([(T日差值 - T日差值均值)^2 + ... + ((T-(N-1))日差值 - (T-(N-1))日差值均值)^2 ]/N)

如果N为20日，则


20日平均值     =  [T日股价 + (T-1)日股价 + ... + (T-19)日股价]/20

计算偏离点


T日差值 > T日差值标准差 * 2

我们以偏离点作为买入信号点，以均线和股价的下一个交点做为卖出信号点。这样我们就把均值回归的投资理论，变成了一个数学模型。

2. 均值回归模型和实现

接下来，我们利用R语言对股票数据的进行操作，来实现一个均值回归模型的实例，从而验证我的们投资理论，是否能发现赚钱的机会。

2.1 数据准备

R语言本身提供了丰富的金融函数工具包，时间序列包zoo和xts，指标计算包TTR，数据处理包plyr，可视包ggplot2等，我们会一起使用这些工具包来完成建模、计算和可视化的工作。关于zoo包和xts包的详细使用可以参考文章，R语言时间序列基础库zoo，可扩展的时间序列xts。

我本次用到的数据是从 况客 直接导出的，况客 会提供各种类型的金融数据API，让开发者可以免费下载。当然，你也可以用quantmod包从Yahoo财经下载。

本文用到的数据，包括A股日K线(向前复权)数据，从2014年7月到2015年日7月，以CSV格式保存到本地文件stock.csv。

数据格式如下：


000001.SZ,2014-07-02,8.14,8.18,8.10,8.17,28604171
000002.SZ,2014-07-02,8.09,8.13,8.05,8.12,40633122
000004.SZ,2014-07-02,13.9,13.99,13.82,13.95,1081139
000005.SZ,2014-07-02,2.27,2.29,2.26,2.28,4157537
000006.SZ,2014-07-02,4.57,4.57,4.50,4.55,5137384
000010.SZ,2014-07-02,6.6,6.82,6.5,6.73,9909143

一共7列：

  • 第1列，股票代码，code，000001.SZ
  • 第2列，交易日期，date，2014-07-02
  • 第3列，开盘价，Open，8.14
  • 第4列，最高价，High，8.18
  • 第5列，最低价，Low，8.10
  • 第6列，收盘价，Close，8.17
  • 第7列，交易量，Volume，28604171

通过R语言加载股票数据，由于数据所有股票都是混合在一起的，而进行计算时又需要按每支票股计算，所以在数据加载时我就进行了转换，按股票代码进行分组，生成R语言的list对象，同时把每支股票的data.frame类型对象转成XTS时间序列类型对象，方便后续的数据处理。


#加载工具包
> library(plyr)
> library(xts)
> library(TTR)
> library(ggplot2)
> library(scales)

# 读取CSV数据文件
> read<-function(file){ 
+   df<-read.table(file=file,header=FALSE,sep = ",", na.strings = "NULL") # 读文件
+   names(df)<-c("code","date","Open","High","Low","Close","Volume")      # 设置列名
+   dl<-split(df[-1],df$code)                                             # 按ccode分组
+   
+   lapply(dl,function(row){                                              # 换成xts类型数据
+     xts(row[-1],order.by = as.Date(row$date))
+   })
+ }

# 加载数据
> data<-read("stock.csv")

# 查看数据类型
> class(data)
[1] "list"

# 查看数据的索引值
> head(names(data))
[1] "000001.SZ" "000002.SZ" "000004.SZ" "000005.SZ" "000006.SZ" "000007.SZ"

# 查看包括的股票数量
> length(data)
[1] 2782

# 查看股票000001.SZ
> head(data[['000001.SZ']])
               Open     High      Low    Close   Volume
2014-07-02 8.146949 8.180000 8.105636 8.171737 28604171
2014-07-03 8.171737 8.254364 8.122162 8.229576 44690486
2014-07-04 8.237838 8.270889 8.146949 8.188263 34231126
2014-07-07 8.188263 8.204788 8.097374 8.146949 34306164
2014-07-08 8.130424 8.204788 8.072586 8.204788 34608702
2014-07-09 8.196525 8.196525 7.915596 7.973434 58789114

把数据准备好了，我们就可以来建立模型了。

2.2 均值回归模型
为了能拉近我们对市场的了解，我们取从2015年1月1日开始的数据，来创建均值回归模型。以平安银行(000001)的为例，画出平安银行的2015年以来的日K线和均线。


# 获得时间范围
> dateArea<-function(sDate=Sys.Date()-365,eDate= Sys.Date(),before=0){  #开始日期，结束日期，提单开始时
+     if(class(sDate)=='character') sDate=as.Date(sDate)
+     if(class(eDate)=='character') eDate=as.Date(eDate)  
+     return(paste(sDate-before,eDate,sep="/"))
+ }
 
# 计算移动平均线
> ma<-function(cdata,mas=c(5,20,60)){
+     if(nrow(cdata)<=max(mas)) return(NULL)
+     ldata<-cdata
+     for(m in mas){
+         ldata<-merge(ldata,SMA(cdata,m))
+     }
+     names(ldata)<-c('Value',paste('ma',mas,sep=''))
+     return(ldata)
+ }

# 日K线和均线
> title<-'000001.SZ'
> SZ000011<-data[[title]]                             # 获得股票数据
> sDate<-as.Date("2015-01-01")                        # 开始日期
> eDate<-as.Date("2015-07-10")                        # 结束日期
> cdata<-SZ000011[dateArea(sDate,eDate,360)]$Close    # 获得收盘价
> ldata<-ma(cdata,c(5,20,60))                         # 选择移动平均指标

# 打印移动平均指标
> tail(ldata)
           Value    ma5    ma20     ma60
2015-07-03 13.07 13.768 15.2545 15.84355
2015-07-06 13.88 13.832 15.1335 15.82700
2015-07-07 14.65 13.854 15.0015 15.79850
2015-07-08 13.19 13.708 14.8120 15.74267
2015-07-09 14.26 13.810 14.6910 15.70867
2015-07-10 14.86 14.168 14.6100 15.67883

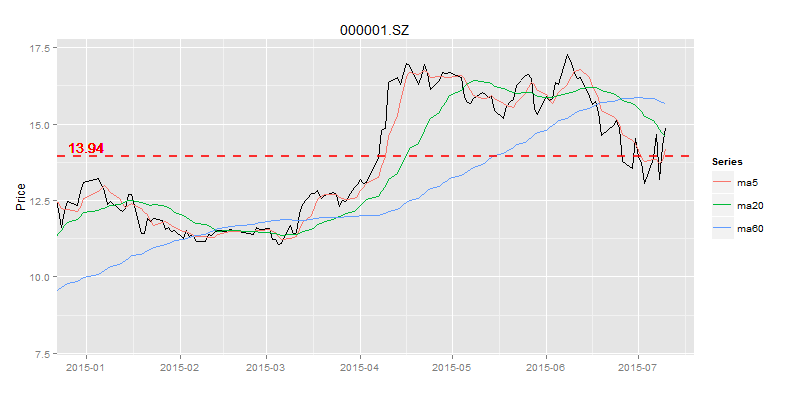
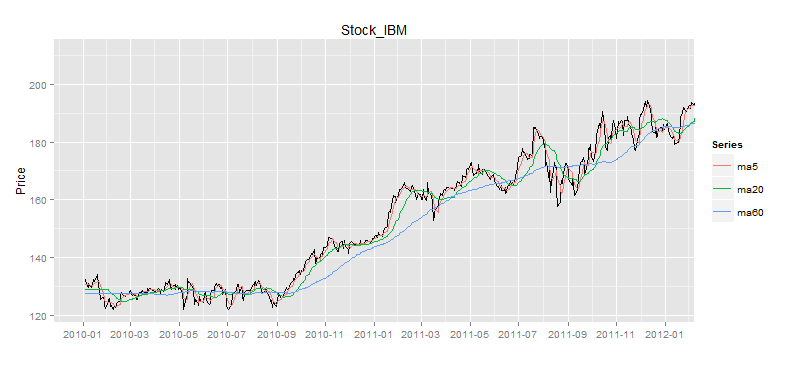
我们设置3条移动平均线，分别是5日平均线，20日平均线，60日平均线，当然也可以按照自己的个性要求设置符合自己的周期。画出日K线和均线图。


> drawLine<-function(ldata,titie="Stock_MA",sDate=min(index(ldata)),eDate=max(index(ldata)),breaks="1 year",avg=FALSE,out=FALSE){
+     if(sDate<min(index(ldata))) sDate=min(index(ldata))
+     if(eDate>max(index(ldata))) eDate=max(index(ldata))  
+     ldata<-na.omit(ldata)
+     
+     g<-ggplot(aes(x=Index, y=Value),data=fortify(ldata[,1],melt=TRUE))
+     g<-g+geom_line()
+     g<-g+geom_line(aes(colour=Series),data=fortify(ldata[,-1],melt=TRUE))
+ 
+     if(avg){
+         meanVal<<-round(mean(ldata[dateArea(sDate,eDate)]$Value),2) # 均值
+         g<-g+geom_hline(aes(yintercept=meanVal),color="red",alpha=0.8,size=1,linetype="dashed")
+         g<-g+geom_text(aes(x=sDate, y=meanVal,label=meanVal),color="red",vjust=-0.4)
+     }
+     g<-g+scale_x_date(labels=date_format("%Y-%m"),breaks=date_breaks(breaks),limits = c(sDate,eDate))
+     g<-g+ylim(min(ldata$Value), max(ldata$Value))
+     g<-g+xlab("") + ylab("Price")+ggtitle(title)
+     g
+ }

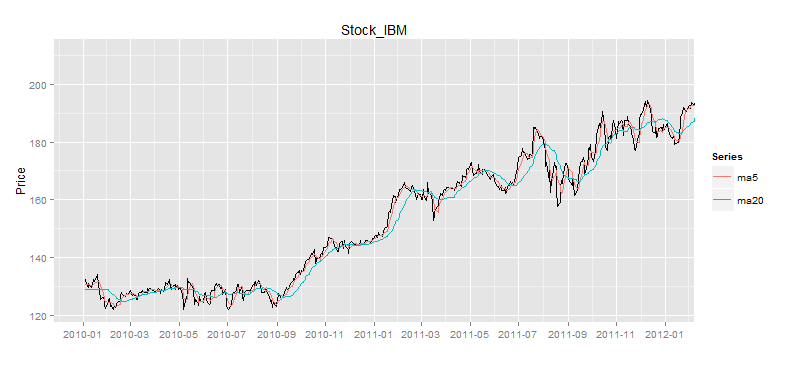
> drawLine(ldata,title,sDate,eDate,'1 month',TRUE)    # 画图

05

如图所示，60日的移动平均线是最平滑的，5日的移动平均线是波动最大的。5日平均线和股价的交叉，明显多于60日平均线和股价的交叉。那么可以说在相同的时间周期内，短周期的移动平均线，比长周期的移动平均线更具有均值回归的特点。

我们分别计算不同周期的，股价与移动平均线的差值的平均标准差。


> getMaSd<-function(ldata,mas=20,sDate,eDate){}) # ...代码省略

# 5日平均线的差值、平均标准差
> ldata5<-getMaSd(ldata,5,sDate,eDate)
> head(ldata5)
              Value      ma5        dif        sd  rate
2015-01-05 13.23673 12.78724 -0.4494869 0.1613198 -2.79
2015-01-06 13.03842 12.89961 -0.1388121 0.1909328 -0.73
2015-01-07 12.79055 12.99215  0.2016081 0.3169068  0.64
2015-01-08 12.36089 12.90292  0.5420283 0.4472248  1.21
2015-01-09 12.46004 12.77733  0.3172848 0.3910700  0.81
2015-01-12 12.20390 12.57076  0.3668606 0.2533165  1.45


# 20日平均线的差值、平均标准差
> ldata20<-getMaSd(ldata,20,sDate,eDate)
> head(ldata20)
              Value     ma20         dif        sd  rate
2015-01-05 13.23673 12.18613 -1.05059293 0.6556366 -1.60
2015-01-06 13.03842 12.23778 -0.80064848 0.6021093 -1.33
2015-01-07 12.79055 12.24810 -0.54244141 0.4754686 -1.14
2015-01-08 12.36089 12.29975 -0.06114343 0.5130410 -0.12
2015-01-09 12.46004 12.33651 -0.12352626 0.5150453 -0.24
2015-01-12 12.20390 12.37163  0.16773131 0.5531618  0.30


# 60日平均线的差值、平均标准差
> ldata60<-getMaSd(ldata,60,sDate,eDate)
> head(ldata60)
              Value     ma60       dif       sd  rate
2015-01-05 13.23673 10.06939 -3.167340 1.264792 -2.50
2015-01-06 13.03842 10.14678 -2.891644 1.271689 -2.27
2015-01-07 12.79055 10.22087 -2.569677 1.269302 -2.02
2015-01-08 12.36089 10.28752 -2.073368 1.258813 -1.65
2015-01-09 12.46004 10.35527 -2.104766 1.247967 -1.69
2015-01-12 12.20390 10.41821 -1.785691 1.233989 -1.45

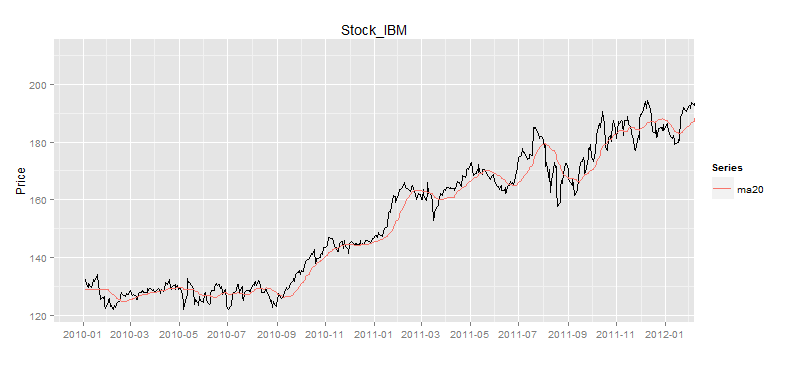
5日的平均线的差值和平均标准差是最小的，而60日的平均线的差值和平均标准差是最大的。如果我们以5日移动平均线做为均值时，会频繁进行交易，但每次收益都很小，可能都不够手续费的成本；另一方面，如果我们以60日移动平均线做为均值时，交易次数会较少，但可能会出现股票成形趋势性上涨或下跌，长时间不能回归的情况，可能会造成现金头寸的紧张。综合上面的2种情况，我们可以选择20日均线作为均值的标的。

根据模型的计算公式，当差值超过2倍的平均标准差时，我们认为股价出现了偏离，以偏离点做为模型的买入信号，当均线和股价再次相交时做为卖出信号。

上一步，我们已经计算出了偏离值，并保存在rate列中。下面我们要找到大于2倍标准化差的点，并画图。


# 差值和平均标准差，大于2倍平均标准差的点
> buyPoint<-function(ldata,x=2,dir=2){})     # ...代码省略

# 画交易信号点
> drawPoint<-function(ldata,pdata,titie,sDate,eDate,breaks="1 year"){
+     ldata<-na.omit(ldata)
+     g<-ggplot(aes(x=Index, y=Value),data=fortify(ldata[,1],melt=TRUE))
+     g<-g+geom_line()
+     g<-g+geom_line(aes(colour=Series),data=fortify(ldata[,-1],melt=TRUE))
+     
+     if(is.data.frame(pdata)){
+         g<-g+geom_point(aes(x=Index,y=Value,colour=op),data=pdata,size=4)
+     }else{
+         g<-g+geom_point(aes(x=Index,y=Value,colour=Series),data=na.omit(fortify(pdata,melt=TRUE)),size=4)  
+     }
+     g<-g+scale_x_date(labels=date_format("%Y-%m"),breaks=date_breaks(breaks),limits = c(sDate,eDate))
+     g<-g+xlab("") + ylab("Price")+ggtitle(title)
+     g
+ }
 
> buydata<-buyPoint(ldata20,2,2)                                       # 多空信号点
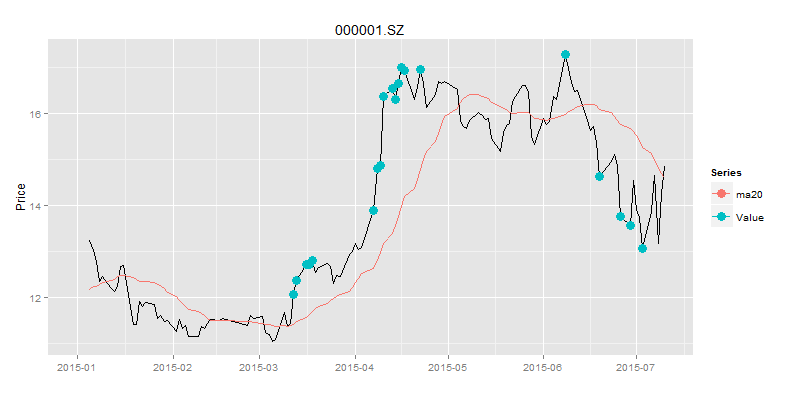
> drawPoint(ldata20[,c(1,2)],buydata$Value,title,sDate,eDate,'1 month')  # 画图

06

图中蓝色的点就是买入的信号点，由于股票我们只能进行单向交易，即低买高卖，并不能直接做空，所以我们要过滤股价高于移动平均线的点，只留下股价低于移动平均线的点，就是我们的买入信号点。

画出买入信号点，只保留股价低于移动平均线的点。


> buydata<-buyPoint(ldata20,2,1)        # 做多信号点
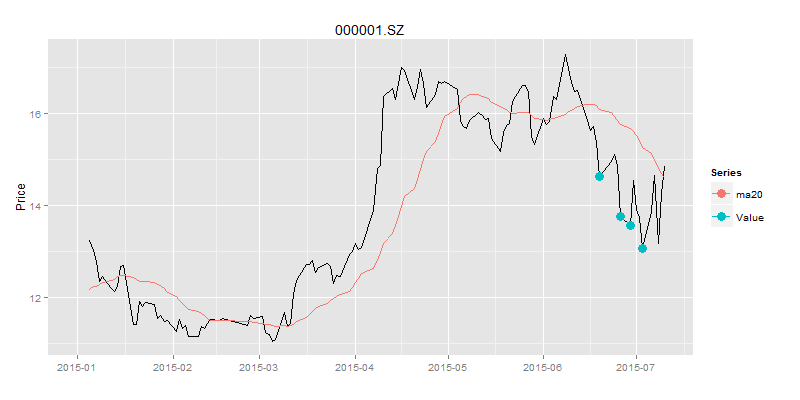
> drawPoint(ldata20[,c(1,2)],buydata$Value,title,sDate,eDate,'1 month') # 画图

07

计算卖出的信号点，当买入后，下一个股价与移动平均线的交点就是卖出的信号点，我们看一下是否可以赚到钱？！


# 计算卖出的信号点
> sellPoint<-function(ldata,buydata){})     # ...代码省略
> selldata<-sellPoint(ldata20,buydata)

# 买出信号
> selldata
           Value  ma20   dif        sd  rate
2015-07-10 14.86 14.61 -0.25 0.7384824 -0.34

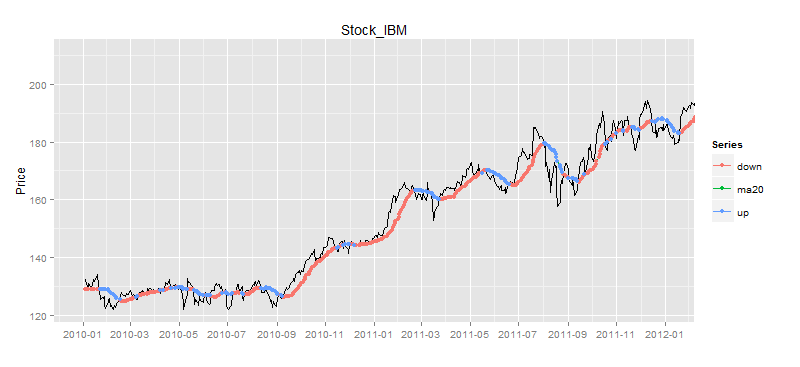
我们把买入信号和卖出信号，合并到一张图上显示，如图所示。


> bsdata<-merge(buydata$Value,selldata$Value)
> names(bsdata)<-c("buy","sell")
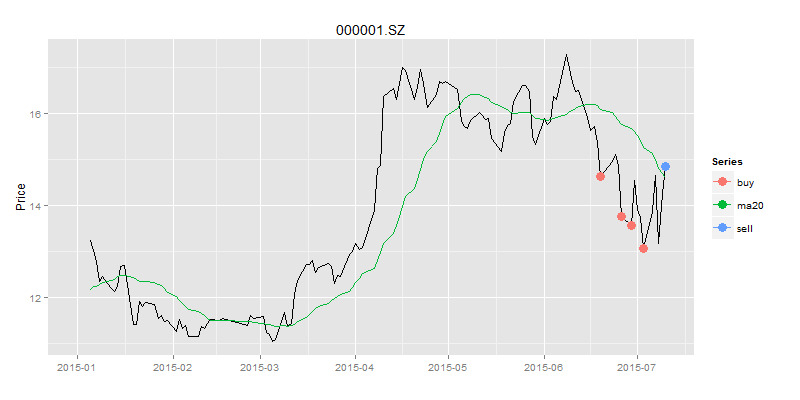
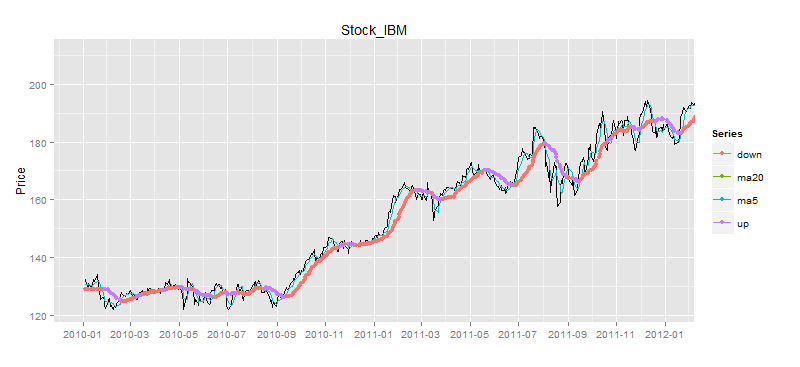
> drawPoint(ldata20[,c(1,2)],bsdata,title,sDate,eDate,'1 month') #画图

08

从图上看，我们在绿色点位置进行买入，而在蓝色点位置进行卖出，确实是赚钱的。那么究竟赚了多少钱呢？我们还需要精确的计算出来。


# 合并交易信号
> signal<-function(buy, sell){})    # ...代码省略

# 交易信号数据
> sdata<-signal(buydata,selldata)                                   
> sdata
           Value    ma20     dif        sd  rate op
2015-06-19 14.63 16.0965  1.4665 0.6620157  2.22  B
2015-06-26 13.77 15.7720  2.0020 0.8271793  2.42  B
2015-06-29 13.56 15.6840  2.1240 0.9271735  2.29  B
2015-07-03 13.07 15.2545  2.1845 1.0434926  2.09  B
2015-07-10 14.86 14.6100 -0.2500 0.7384824 -0.34  S

利用交易信号数据，进行模拟交易。我们设定交易参数和规则：

  • 以10万元人民币为本金
  • 买入信号出现时，以收盘价买入，每次买入价值1万元的股票。如果连续出现买入信号，则一直买入。若现金不足1万元时，则跳过买入信号。
  • 卖出信号出现时，以收盘价卖出，一次性平仓信号对应的股票。
  • 手续费为0元

# 模拟交易
> trade<-function(sdata,capital=100000,fixMoney=10000){})    # ...代码省略

# 交易结果
> result<-trade(sdata,100000,10000)

来看一下，每笔交易的明细。


> result$ticks
           Value    ma20     dif        sd  rate op      cash amount     asset     diff
2015-06-19 14.63 16.0965  1.4665 0.6620157  2.22  B  90007.71    683 100000.00     0.00
2015-06-26 13.77 15.7720  2.0020 0.8271793  2.42  B  80010.69   1409  99412.62  -587.38
2015-06-29 13.56 15.6840  2.1240 0.9271735  2.29  B  70016.97   2146  99116.73  -295.89
2015-07-03 13.07 15.2545  2.1845 1.0434926  2.09  B  60018.42   2911  98065.19 -1051.54
2015-07-10 14.86 14.6100 -0.2500 0.7384824 -0.34  S 103275.88      0 103275.88  5210.69

一共发生了5笔交易，其中4笔买入，1笔卖出。最后，资金剩余103275.88元，赚了3275.88元，收益率3.275%。

在卖出时，赚钱的交易有1笔。


> result$rise
           Value  ma20   dif        sd  rate op     cash amount    asset    diff
2015-07-10 14.86 14.61 -0.25 0.7384824 -0.34  S 103275.9      0 103275.9 5210.69

在卖出时，赔钱的交易，没有发生。


> result$fall
 [1] Value  ma20   dif    sd     rate   op     cash   amount asset  diff  
<0 行> (或0-长度的row.names)

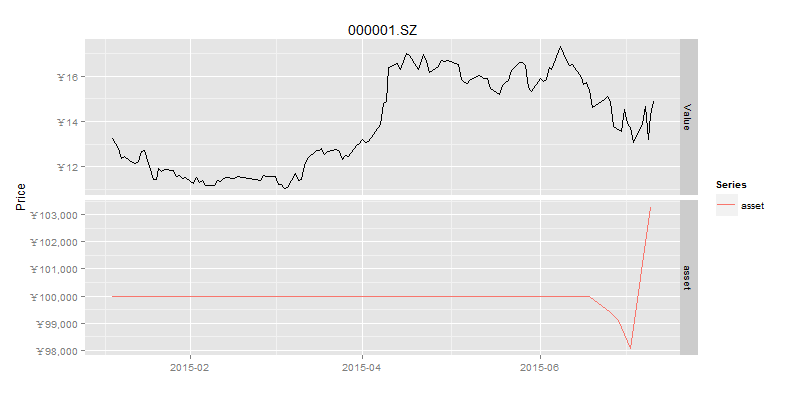
接下来，我们再对比一下，资产净值和股价。


# 资产净值曲线
> drawAsset<-function(ldata,adata,sDate=FALSE,capital=100000){
+     if(!sDate) sDate<-index(ldata)[1]
+     adata<-rbind(adata,as.xts(capital,as.Date(sDate)))
+     
+     g<-ggplot(aes(x=Index, y=Value),data=fortify(ldata[,1],melt=TRUE))
+     g<-g+geom_line()
+     g<-g+geom_line(aes(x=as.Date(Index), y=Value,colour=Series),data=fortify(adata,melt=TRUE))
+     g<-g+facet_grid(Series ~ .,scales = "free_y")
+     g<-g+scale_y_continuous(labels=dollar_format(prefix = "￥"))
+     g<-g+scale_x_date(labels=date_format("%Y-%m"),breaks=date_breaks("2 months"),limits = c(sDate,eDate))
+     g<-g+xlab("") + ylab("Price")+ggtitle(title)
+     g
+ }

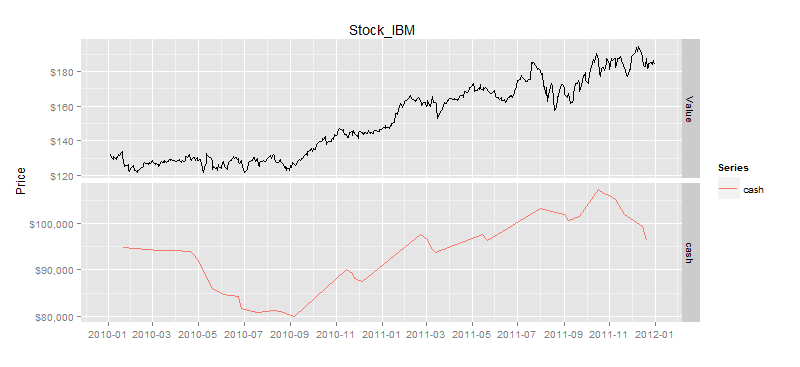
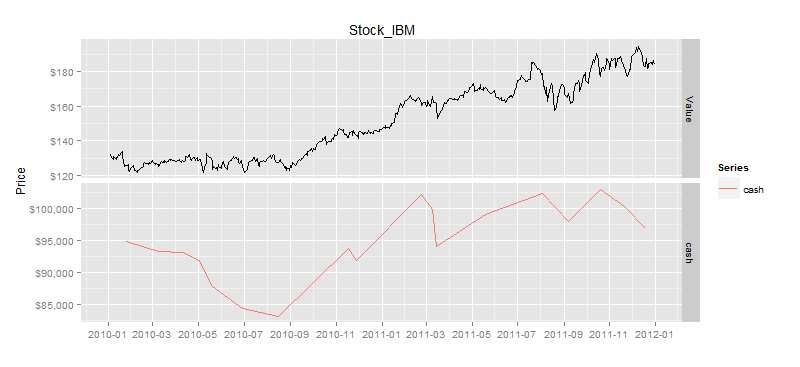
> drawAsset(ldata20,as.xts(result$ticks['asset']))  # 资产净值曲线

09

刚才我们是对一支股票进行了测试，发现是有机会的，那么我再换另外一支股票，看一下是否用同样的效果呢？我们把刚才数据操作的过程，封装到统一的quick函数，就可以快速验证均值回归在其他股票的表现情况了。


> quick<-function(title,sDate,eDate){}  # ...代码省略

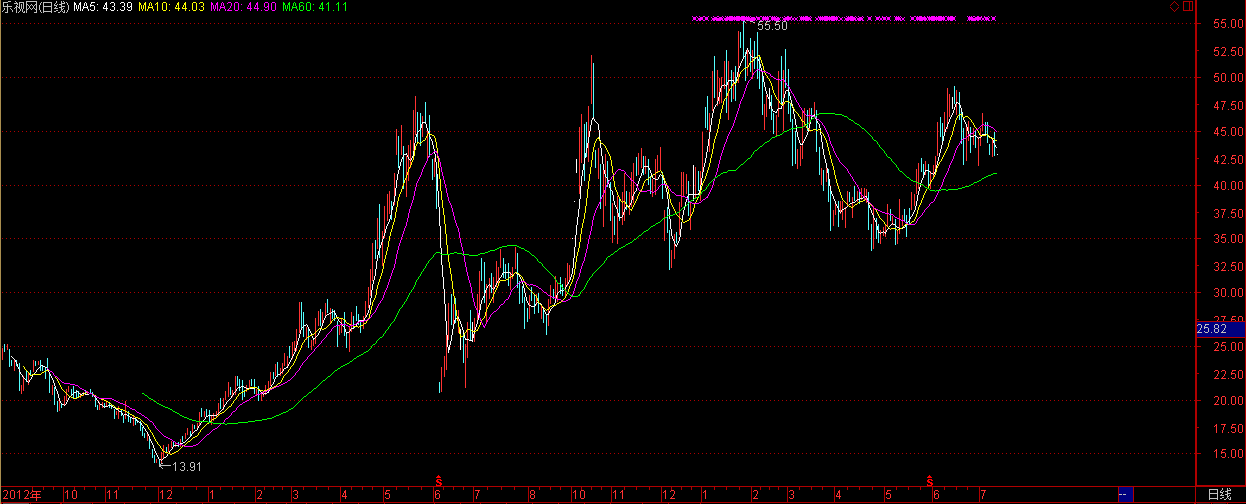
我们用乐视网(300104)试一下，看看有没有赚钱的机会！！


> title<-"300104.SZ"
> sDate<-as.Date("2015-01-01") #开始日期
> eDate<-as.Date("2015-07-10") #结束日期

> quick(title,sDate,eDate)
$ticks
           Value    ma20     dif       sd  rate op      cash amount     asset     diff
2015-06-19 55.04 69.9095 14.8695 5.347756  2.78  B  90037.76    181 100000.00     0.00
2015-06-23 54.30 68.8075 14.5075 5.477894  2.65  B  80046.56    365  99866.06  -133.94
2015-06-24 56.21 67.8735 11.6635 5.404922  2.16  B  70097.39    542 100563.21   697.15
2015-06-25 51.80 66.8775 15.0775 5.770806  2.61  B  60099.99    735  98172.99 -2390.22
2015-06-26 46.79 65.9830 19.1930 6.580622  2.92  B  50133.72    948  94490.64 -3682.35
2015-06-29 47.05 64.9445 17.8945 7.096230  2.52  B  40159.12   1160  94737.12   246.48
2015-07-07 47.86 58.8150 10.9550 5.401247  2.03  B  30204.24   1368  95676.72   939.60
2015-07-10 57.92 57.3520 -0.5680 5.625309 -0.10  S 109438.80      0 109438.80 13762.08

$rise
           Value   ma20    dif       sd rate op     cash amount    asset     diff
2015-07-10 57.92 57.352 -0.568 5.625309 -0.1  S 109438.8      0 109438.8 13762.08

$fall
 [1] Value  ma20   dif    sd     rate   op     cash   amount asset  diff  
<0 行> (或0-长度的row.names)

从数据结果看，我们又赚到了。一共发生了8笔交易，其中7笔买入，1笔卖出。最后，资金剩余109438.80元，赚了9438.80元，收益率9.43%。

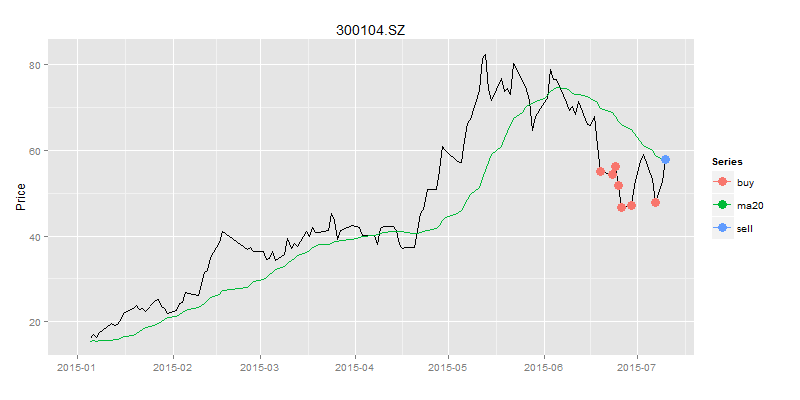
画出交易信号图


> title<-"300104.SZ"
> sDate<-as.Date("2015-01-01") #开始日期
> eDate<-as.Date("2015-07-10") #结束日期

> stock<-data[[title]]
> cdata<-stock[dateArea(sDate,eDate,360)]$Close
> ldata<-ma(cdata,c(20))
> ldata<-getMaSd(ldata,20,sDate,eDate)
> buydata<-buyPoint(ldata,2,1)  
> selldata<-sellPoint(ldata,buydata)
> bsdata<-merge(buydata$Value,selldata$Value)
> drawPoint(ldata[,c(1,2)],bsdata,title,sDate,eDate,'1 month') #画图

10

在恐慌的6月份，当别人都被套牢30%以上的情况下，我们还朿9%正收益，那么应该是多么舒心的一件事情啊！！

3. 量化选股

上文中，我们用2支股票进行了测试，发现均值回归模型是适合于股票交易的。如果我们利用模型对全市场的股票进行扫描，应用会产生更多的交易信号，找到更多的投资机会，这样我们就能如何能获得更大的收益。

那么，接下来我们就根据均值回归的理论进行量化选股。

根据我们之前的经验，当股价与平均标准差的偏离越大，有可能带来的收益就越大。那么通过量化的手段，在整个的市场2700多支股票中，把每天偏离最大股票的找出来进行交易，就可以有效地分配我们的资金，进行更有效的投资。我们要试一下，市场是否是和我们的思路是一致的。

对全市场股票进行扫描，首先计算差值、平均值和平均标准差。


> sDate<-as.Date("2015-01-01")                # 开始日期
> eDate<-as.Date("2015-07-10")                # 结束日期

# 计算差值、平均值和平均标准差
> data0<-lapply(data,function(stock){})       # 代码省略

# 去掉空数据
> data0<-data0[!sapply(data0, is.null)]      

# 全市场股票
> length(data)
[1] 2782

# 有效的股票
> length(data0)
[1] 2697

# 查看第1支股票
> head(data0[[1]])
              Value     ma20         dif        sd  rate
2015-01-05 13.23673 12.18613 -1.05059293 0.6556366 -1.60
2015-01-06 13.03842 12.23778 -0.80064848 0.6021093 -1.33
2015-01-07 12.79055 12.24810 -0.54244141 0.4754686 -1.14
2015-01-08 12.36089 12.29975 -0.06114343 0.5130410 -0.12
2015-01-09 12.46004 12.33651 -0.12352626 0.5150453 -0.24
2015-01-12 12.20390 12.37163  0.16773131 0.5531618  0.30

第一次扫描后，有2697支股票是符合条件的，有85支股票由于数据样本不足被排除。

接下来，继续对2697支股票进行筛选，找到符合要求的买入信号点。


# 计算买入信号
> buys<-lapply(data0,function(stock){})  # ...代码省略 

# 去掉空数据
> buys<-buys[!sapply(buys, is.null)] 

# 查看有买入信号的股票
> length(buys)
[1] 1819

# 查看买入信号
> head(buys)
$`000001.SZ`
           Value    ma20    dif        sd rate
2015-06-19 14.63 16.0965 1.4665 0.6620157 2.22
2015-06-26 13.77 15.7720 2.0020 0.8271793 2.42
2015-06-29 13.56 15.6840 2.1240 0.9271735 2.29
2015-07-03 13.07 15.2545 2.1845 1.0434926 2.09

$`000002.SZ`
           Value   ma20   dif        sd rate
2015-03-05 11.90 12.568 0.668 0.2644101 2.53
2015-03-06 11.94 12.509 0.569 0.2674732 2.13

$`000004.SZ`
           Value    ma20     dif        sd rate
2015-01-05 15.69 17.7210  2.0310 0.7395717 2.75
2015-07-06 26.03 39.1540 13.1240 6.3898795 2.05
2015-07-07 23.43 38.2025 14.7725 6.9421723 2.13
2015-07-08 22.22 37.2635 15.0435 7.4287088 2.03

$`000005.SZ`
           Value    ma20    dif       sd rate
2015-07-06  6.02 10.9600 4.9400 2.381665 2.07
2015-07-07  5.42 10.5655 5.1455 2.333008 2.21

$`000006.SZ`
              Value     ma20       dif      sd rate
2015-01-19 5.829283 6.519462 0.6901792 0.26929 2.56

$`000007.SZ`
           Value    ma20    dif        sd rate
2015-02-06 12.47 14.4200 1.9500 0.6182860 3.15
2015-02-09 12.52 14.3270 1.8070 0.7440473 2.43
2015-02-10 12.10 14.1845 2.0845 0.8484250 2.46

通过计算发现，有1819支股票，在这半年中产生过买入信号。每支股票产生的买入信号的时间和频率都是不同，这样我们就可以把钱分散投资到不同的股票上，同时分散风险。如果交易信号同一天出现在多支的股票上，而我们资金有限，又想让收益最大化，那么我们可以选择偏离值最大的股票进行交易。

接下来，我们用程序找到每日偏离最大的股票。


# 合并数据，从list转型到data.frame
buydf<-ldply(buys,function(e){})    # ...代码省略

# 选出同一日rate最大的股票，做为买入信号
buydatas<-ddply(buydf, .(date), function(row){}) # ...代码省略

# 查看买入信号
> nrow(buydatas)
[1] 81

# 查看买入信号细节
> head(buydatas)
         .id       date      Value       ma20        dif         sd rate
1  002551.SZ 2015-01-05  16.573846  19.565446  2.9916000 0.74591596 4.01
2  002450.SZ 2015-01-06  18.548809  19.766636  1.2178275 0.34008453 3.58
3  300143.SZ 2015-01-07  11.480000  12.603000  1.1230000 0.32028018 3.51
4  300335.SZ 2015-01-08  12.113677  13.139601  1.0259238 0.21760484 4.71
5  300335.SZ 2015-01-09  12.243288  13.043888  0.8005994 0.22940845 3.49
6  300335.SZ 2015-01-12  11.994036  12.941694  0.9476584 0.23168313 4.09

最后，我们选出81个买入信号点，基本上每个交易日都是买入信号。有了买入信号，继续找到卖出信号。


# 卖出信号
> selldatas<-data.frame()     # ...代码省略

# 卖出信号去重
> selldatas<-unique(selldatas)  
> nrow(selldatas)
[1] 33

# 查看买出信号
> head(selldatas)
                Value      ma20         dif        sd  rate       .id       date op
2015-01-12  19.232308 18.848908 -0.38340000 0.9051374 -0.42 002551.SZ 2015-01-12  S
2015-01-08  19.814257 19.729006 -0.08525126 0.3782955 -0.23 002450.SZ 2015-01-08  S
2015-01-28  11.210000 11.019500 -0.19050000 0.7781848 -0.24 300143.SZ 2015-01-28  S
2015-01-21  13.190448 12.899321 -0.29112706 0.3871871 -0.75 300335.SZ 2015-01-21  S
2015-01-213  7.140000  6.989500 -0.15050000 0.2007652 -0.75 002505.SZ 2015-01-21  S
2015-01-22   5.561561  5.490668 -0.07089242 0.2127939 -0.33 600077.SH 2015-01-22  S

通过计算，一共有33个买出信号点。最后，合并买入信号和卖出信号，并计算收益。


> buydatas$op<-'B'                              # 买入标志
> selldatas$op<-'S'                             # 卖出标志
> sdatas<-rbind(buydatas,selldatas)             # 合并数据
> row.names(sdatas)<-1:nrow(sdatas)             # 重设行号
> sdatas<-sdatas[order(sdatas$.id),]            # 按股票代码排序

# 查看合并的信号
> head(sdatas)
          .id       date Value     ma20       dif         sd  rate op
36  000002.SZ 2015-03-05 11.90 12.56800  0.668000 0.26441011  2.53  B
100 000002.SZ 2015-03-16 12.49 12.38050 -0.109500 0.23702768 -0.46  S
58  000553.SZ 2015-05-06 14.35 15.50882  1.158824 0.38429912  3.02  B
110 000553.SZ 2015-05-21 16.57 15.18903 -1.380972 0.55647152 -2.48  S
26  000725.SZ 2015-02-09  2.80  3.11400  0.314000 0.07934585  3.96  B
94  000725.SZ 2015-02-16  3.09  3.06500 -0.025000 0.08182388 -0.31  S

最后，按照股票进行分组，分别计算个股的收益。


# 计算个股的收益
> slist<-split(sdatas[-1],sdatas$.id)      # 按股票代码分组
> results<-lapply(slist,trade)

# 查看信号的股票
> names(results)
 [1] "000002.SZ" "000553.SZ" "000725.SZ" "000786.SZ" "000826.SZ" "002240.SZ" "002450.SZ"
 [8] "002496.SZ" "002505.SZ" "002544.SZ" "002551.SZ" "002646.SZ" "002652.SZ" "300143.SZ"
[15] "300335.SZ" "300359.SZ" "300380.SZ" "300397.SZ" "300439.SZ" "300440.SZ" "300444.SZ"
[22] "600030.SH" "600038.SH" "600077.SH" "600168.SH" "600199.SH" "600213.SH" "600375.SH"
[29] "600490.SH" "600536.SH" "600656.SH" "600733.SH" "600890.SH" "601179.SH" "601186.SH"
[36] "601628.SH" "601633.SH" "601939.SH" "603019.SH"

我们查看万科A(000002)的股票。


> results[['000002.SZ']]$ticks
          date Value    ma20     dif        sd  rate op     cash amount    asset  diff
36  2015-03-05 11.90 12.5680  0.6680 0.2644101  2.53  B  90004.0    840 100000.0   0.0
100 2015-03-16 12.49 12.3805 -0.1095 0.2370277 -0.46  S 100495.6      0 100495.6 495.6

通过优化的规则设计，一共有2笔交易，赚了495元。如要我们没有进行算法优化，一直交易万科A，那么会发生3笔交易，我们可以赚955.95元。


> quick('000002.SZ',sDate,eDate)$ticks
           Value    ma20     dif        sd  rate op      cash amount    asset   diff
2015-03-05 11.90 12.5680  0.6680 0.2644101  2.53  B  90004.00    840 100000.0   0.00
2015-03-06 11.94 12.5090  0.5690 0.2674732  2.13  B  80010.22   1677 100033.6  33.60
2015-03-16 12.49 12.3805 -0.1095 0.2370277 -0.46  S 100955.95      0 100955.9 922.35

本文到此就要结束了！但其实还有很多的事情要做，比如对模型参数的优化，用10日均线代替20日均线，用3倍标准差偏移代替2倍标准差偏移，对样本进行正态分布的检验，结合其他趋势类模型共同产生信号等，这些就不是一篇文章可以解决的事情了。大家可以况客金融平台的网站上，发现更多不一样的策略。

本文从均值回归的理论的介绍开始，到市场特征检验，再到数学公式，R语言建模，历史数据回测，最后找到投资机会，是一套完整的从理论到实践的学习方法。虽然困难重重，但做为有理想的极客，我们是有能力来克服这些困难的。

本文同时用到了计算机、金融、数学、统计等多学科知识的结合，我认为这是技术复合人才未来的发展方向。如果说过去10年是房地产的黄金10年，那么未来的10年将是金融的黄金10年。当我们IT人掌握了足够的金融知识，一定会有能力去金融市场抢钱的。

抓住机会！！程序员，加油！

######################################################
看文字不过瘾，作者视频讲解，请访问网站：http://onbook.me/video
######################################################

转载请注明出处：
http://blog.fens.me/finance-mean-reversion/

打赏作者

Posted:
Jul 11, 2014
Tags:
Comments:
53 Comments

二条均线打天下

用IT技术玩金融系列文章，将介绍如何使用IT技术，处理金融大数据。在互联网混迹多年，已经熟练掌握一些IT技术。单纯地在互联网做开发，总觉得使劲的方式不对。要想靠技术养活自己，就要把技术变现。通过“跨界”可以寻找新的机会，创造技术的壁垒。

金融是离钱最近的市场，也是变现的好渠道！今天就开始踏上“用IT技术玩金融”之旅！

关于作者：

  • 张丹(Conan), 程序员Java,R,PHP,Javascript
  • weibo：@Conan_Z
  • blog: http://blog.fens.me
  • email: bsspirit@gmail.com

转载请注明出处：
http://blog.fens.me/finance-stock-ma/

stock-ma

前言

移动平均线(MA)是股市中最常用的一种技术分析方法，用来在大行情的波动段找到有效的交易信号。移动平均线不仅简单，而且有效，对股市操作具有神奇的指导作用。

据金融从业人员称，均线模型能有效地打败了大部分的主观策略，是炒股、炒期货的必备基本工具。那么本文将深入研究一下均线模型，如何在股市中发挥作用。

目录

  1. 移动平均线
  2. 均线模型
  3. 用R语言实现均线模型

1. 移动平均线

移动平均线(MA,Moving average）是以道·琼斯的”平均成本概念”为理论基础，采用统计学中”移动平均”的原理，将一段时期内的股票价格平均值连成曲线，用来显示股价的历史波动情况，进而反映股价指数未来发展趋势的技术分析方法。它是道氏理论的形象化表述。

移动平均线的计算方法就是求连续若干天的收盘价的算术平均。天数就是MA的参数。在技术分析领域中，移动平均线是必不可少的指标工具。移动平均线利用统计学上的“移动平均”原理，将每天的市场价格进行移动平均计算，求出一个趋势值，用来作为价格走势的研判工具。

计算公式： MA = (C1+C2+C3+C4+C5+….+Cn)/n ,C为收盘价，n为移动平均周期数例如，5日移动平均价格计算方法为：


MA5 = （前四天收盘价+前三天收盘价+前天收盘价+昨天收盘价+今天收盘价）/5

移动平均线依时间长短可分为三种，即短期移动平均线，中期移动平均线，长期移动平均线。短期移动平均线一般以5日或10日为计算期间，中期移动平均线大多以30日、60日为计算期间；长期移动平均线大多以100天和200天为计算期间。

移动平均根据对数据的处理方法，又可分为3种：

  • 简单移动平均线(SMA)：又称“算术移动平均线”，是指对特定期间的收盘价进行简单平均化的意思。一般所提及之移动平均线即指简单移动平均线(SMA)。
  • 加权移动平均线(WMA):加权移动平均线(Weighted Moving Average 简称WMA)，是一种按时间进行加权运算的移动平均线。时间越近越近的价格，权重越大。计算方式是基于加权移动平均线日数，将每一个之前日 数比重提升。每一价格会乘以一个比重，最新的价格会有最大的比重，其之前的每一日的比重将会递减。加权移动平均线是移动平均线(MA)的改良。
  • 指数平滑移动平均线(EMA):指数平滑移动平均线EXPMA(Exponential Moving Average)，为解决一旦价格已脱离均线差值扩大，而平均线未能立即反应，EXPMA可以减少类似缺点。

2. 均线模型

在日K线图中除了标准的价格K线以外，另外还有4条线，分别是白线、黄线、紫线、绿线依次分别表示：5日、10日、20日和60日移动平均线，通过这4条线与价格K线的交叉，就可以形成不同的均线模型。

以乐视网(300104)股票日K图为例，截取2012年8月到2014年7月的股价数据。
300104

最低价是13.91，出现在2012年12月；最高价55.50，出现在2014年1月。这段时期，可以看到乐视网的股价一路震荡向上，绿色线为60日均线平滑了股价，趋势性比较明显。

利用均线平滑的特点，可以发现均线与价格K线会有叉，各均线之间也有交叉，我们可以通过这些交叉点判断交易信号。

  • 黄金交叉，当10日均线由下往上穿越30日均线，10日均线在上，30日均线在下，其交叉点就是黄金交叉，黄金交叉是多头的表现，出现黄金交叉后，后市会有一定的涨幅空间，这是进场的最佳时机。
  • 死亡交叉，当30日均线与10日平均线交叉时，30日均线由下住上穿越10日平均线，形成30日平均线在上，10日均线在下时，其交点称之为”死亡交叉”，”死亡交叉”预示空头市场来临，股市将下跌此时是出场的最佳时机。

如果很好地运用移动平均线理论，再掌握行情的真正趋势，就能实现获取可观利润。

但移动平均线理论也有局限性：

  • 移动平均线是股价定型后产生的图形，反映较慢，只适用于日间交易。
  • 移动平均线不能反映股价在当日的变化及成交量的大小，不适用于日内交易。
  • 移动平均线是趋势性模型，如果股价未形成趋势，只是频繁波动，模型不适用。

3. 用R语言实现均线模型

接下来，我们利用R语言对股票数据的进行操作，来实现一个均线模型的实例。

3.1 从互联网下载数据

R语言本身提供了丰富的金融函数工具包，quantmod包就是最常用的一个，另外还要配合时间序列包zoo和xts，指标计算包TTR，可视包ggplot2等一起使用。关于zoo包和xts包的详细使用可以参考文章R语言时间序列基础库zoo，可扩展的时间序列xts。

我们首先利用quantmod包，从互联网下载股票数据，并以CSV格式保存到本地。


#加载工具包
> library(plyr)
> library(quantmod)
> library(TTR)
> library(ggplot2)
> library(scales)

#下载数据
> download<-function(stock,from="2010-01-01"){
+ df<-getSymbols(stock,from=from,env=environment(),auto.assign=FALSE)  #下载数据
+ names(df)<-c("Open","High","Low","Close","Volume","Adjusted")
+ write.zoo(df,file=paste(stock,".csv",sep=""),sep=",",quote=FALSE) #保存到本地
+}

#本地读数据
> read<-function(stock){  
+  as.xts(read.zoo(file=paste(stock,".csv",sep=""),header = TRUE,sep=",", format="%Y-%m-%d"))
+}

> stock<-"IBM"
> download(stock,from='2010-01-01')
> IBM<-read(stock)

# 查看数据类型
> class(IBM)
[1] "xts" "zoo"

# 查看前6条数据
> head(IBM)
             Open   High    Low  Close  Volume Adjusted
2010-01-04 131.18 132.97 130.85 132.45 6155300   121.91
2010-01-05 131.68 131.85 130.10 130.85 6841400   120.44
2010-01-06 130.68 131.49 129.81 130.00 5605300   119.66
2010-01-07 129.87 130.25 128.91 129.55 5840600   119.24
2010-01-08 129.07 130.92 129.05 130.85 4197200   120.44
2010-01-11 131.06 131.06 128.67 129.48 5730400   119.18

利用quantmod包的getSymbols()函数，默认会通过Yahoo的金融开放API下载数据，我们选择IBM的股票数据，从2010-01-01到今天2014-07-09的4年多的日间交易数据。数据类型为xts格式的时间序列，数据包括7个列，以日期做索引列，其他6列分别为 开盘价(Open), 最高价(High), 最低价(Low), 收盘价(Close), 交易量(Volume), 调整价(Adjusted)。

3.2 实现简单的蜡烛图

直接使用quantmod包的chartSeries()函数，我们可以画出可视化效果还不错的蜡烛图。

简单的蜡烛图


> chartSeries(IBM)

ibm_1

带指标的蜡烛图


> chartSeries(IBM,TA = "addVo(); addSMA(); addEnvelope();addMACD(); addROC()")

ibm_2

非常简单的2个函数，就可以实现股票数据的可视化。当然，这个功能是封装好的通用的函数，如果我们要自定策略模型，就需要自己写代码来实现了，比如 自定义的支持量化机(SVM)分类器模型，不过我们今天不讲太复杂的模型，而是实现均线模型。

3.3 自定义均线图

通过自定义的方式，我们就可以脱离quantmod包了。

我们需要自定义均线指标：

  • 日期时间序列为索引
  • 收盘价做为价格指标
  • 不考虑成交量及其他维度字段
  • 取2010-01-01至2012-01-01，形成趋势的数据
  • 画出价格曲线，5日均线，20日均线，60日是均线

R语言程序实现


#移动平均
> ma<-function(cdata,mas=c(5,20,60)){ 
+     ldata<-cdata
+     for(m in mas){
+         ldata<-merge(ldata,SMA(cdata,m))
+     }
+     ldata<-na.locf(ldata, fromLast=TRUE)
+     names(ldata)<-c('Value',paste('ma',mas,sep=''))
+     return(ldata)
+ }

# 均线图
> drawLine<-function(ldata,titie="Stock_MA",sDate=min(index(ldata)),eDate=max(index(ldata)),out=FALSE){
+     g<-ggplot(aes(x=Index, y=Value),data=fortify(ldata[,1],melt=TRUE))
+     g<-g+geom_line()
+     g<-g+geom_line(aes(colour=Series),data=fortify(ldata[,-1],melt=TRUE))
+     g<-g+scale_x_date(labels=date_format("%Y-%m"),breaks=date_breaks("2 months"),limits = c(sDate,eDate))
+     g<-g+xlab("") + ylab("Price")+ggtitle(title)
+     
+     if(out) ggsave(g,file=paste(titie,".png",sep=""))
+     else g
+ }

# 运行程序
> cdata<-IBM['2010/2012']$Close
> title<-"Stock_IBM" #图片标题
> sDate<-as.Date("2010-1-1") #开始日期
> eDate<-as.Date("2012-1-1") #结束日期

> ldata<-ma(cdata,c(5,20,60))  #选择滑动平均指标
> drawLine(ldata,title,sDate,eDate) #画图

maline

通过自己封装的移动平均函数和可视化函数，就实现了与交易软件中类似的日K线图和多条均线结合的可视化输出。

3.4 一条均线的交易策略

基于上面的定义的均线函数，我们就可以设计自己的交易策略模型了。

模型设计思路：

  • 1. 以股价和20日均线的交叉，进行交易信号的判断。
  • 2. 当股价上穿20日均线则买入(红色)，下穿20日均线卖出(蓝色)。

画出股价和20日均线图


> ldata<-ma(cdata,c(20))  #选择滑动平均指标
> drawLine(ldata,title,sDate,eDate) #画图

line1_1

以散点覆盖20日均线，红色点为买入持有，蓝色点为卖出空仓。


# 均线图+散点
> drawPoint<-function(ldata,pdata,titie,sDate,eDate){
+   g<-ggplot(aes(x=Index, y=Value),data=fortify(ldata[,1],melt=TRUE))
+   g<-g+geom_line()
+   g<-g+geom_line(aes(colour=Series),data=fortify(ldata[,-1],melt=TRUE))
+   g<-g+geom_point(aes(x=Index,y=Value,colour=Series),data=fortify(pdata,melt=TRUE))
+   g<-g+scale_x_date(labels=date_format("%Y-%m"),breaks=date_breaks("2 months"),limits = c(sDate,eDate))
+   g<-g+xlab("") + ylab("Price")+ggtitle(title)
+   g
+ }

# 散点数据
> genPoint<-function(pdata,ldata){} #代码省略
> pdata<-genPoint(pdata,ldata)
> head(pdata)
       Index Series    Value
1 2010-01-04   down 128.7955
2 2010-01-05   down 128.7955
3 2010-01-06   down 128.7955
4 2010-01-07   down 128.7955
5 2010-01-08   down 128.7955
6 2010-01-11   down 128.7955

> drawPoint(ldata,pdata,title,sDate,eDate) #画图

line1_2

用股价和20日均线价格做比较，把股价大于均线的部分用蓝色表示，股价小于均线的部分用红色表示。我们看到图中，蓝色点和红色点在20日均线上交替出现，我们可以在每次红色出现的第一个点买入股票，然后在蓝色的第一个点卖出股票，直观看上去的感觉还是不错的。

我们要找出这些交易信号点，做量化的统计，看看到底能不能赚钱。


#交易信号
> Signal<-function(cdata,pdata){} #代码省略
> tdata<-Signal(cdata,pdata)
> tdata<-tdata[which(as.Date(row.names(tdata)) head(tdata)
            Value op
2010-01-04 132.45  B
2010-01-22 125.50  S
2010-02-17 126.33  B
2010-03-09 125.55  S
2010-03-11 127.60  B
2010-04-08 127.61  S

# 交易记录
> nrow(tdata)
[1] 72

一共有72条交易记录，买卖各占一半。

接下来，我们要利用交易信号数据，进行模拟交易。我们设定交易参数，以$10W为本金，满仓买入或卖出，手续为0，传入交易信号。


#模拟交易
#参数：交易信号,本金,持仓比例,手续费比例
> trade<-function(tdata,capital=100000,position=1,fee=0){} #代码省略
> result1<-trade(tdata,100000)

# 查看每笔交易
> head(result1$ticks)
            Value op     cash amount     asset     diff
2010-01-04 132.45  B     0.25    755 100000.00     0.00
2010-01-22 125.50  S 94752.75      0  94752.75 -5247.25
2010-02-17 126.33  B     5.25    750  94752.75     0.00
2010-03-09 125.55  S 94167.75      0  94167.75  -585.00
2010-03-11 127.60  B   126.55    737  94167.75     0.00
2010-04-08 127.61  S 94175.12      0  94175.12     7.37

# 盈利的交易
> head(result1$rise)
            Value op     cash amount    asset     diff
2010-03-11 127.60  B   126.55    737 94167.75     0.00
2010-04-08 127.61  S 94175.12      0 94175.12     7.37
2010-07-22 127.47  B   108.79    633 80797.30     0.00
2010-08-12 128.30  S 81322.69      0 81322.69   525.39
2010-09-09 126.36  B   120.40    632 79979.92     0.00
2010-11-16 142.24  S 90016.08      0 90016.08 10036.16

# 亏损的交易
> head(result1$fall)
            Value op     cash amount     asset     diff
2010-01-04 132.45  B     0.25    755 100000.00     0.00
2010-01-22 125.50  S 94752.75      0  94752.75 -5247.25
2010-02-17 126.33  B     5.25    750  94752.75     0.00
2010-03-09 125.55  S 94167.75      0  94167.75  -585.00
2010-04-09 128.76  B    51.56    731  94175.12     0.00
2010-04-12 128.36  S 93882.72      0  93882.72  -292.40

通过模拟交易，我们就能精确地算出每笔交易的盈利情况了。你相信么，有56笔交易其实是亏损的，16笔交易是有盈利的。

查看最后的资金情况。


> tail(result1$ticks,1)
            Value op     cash amount    asset     diff
2011-12-21 181.47  S 96363.76      0 96363.76 -3063.87

最后，资金剩余96363.76元，也就是我们亏了3636.24元。

为什么最后会亏损呢？中间的大波段应该赚到了足够多的钱。通过资金曲线我们可以找到亏损的原因。

画出资金曲线


# 股价+现金流量
> drawCash<-function(ldata,adata){
+   g<-ggplot(aes(x=Index, y=Value),data=fortify(ldata[,1],melt=TRUE))
+   g<-g+geom_line()
+   g<-g+geom_line(aes(x=as.Date(Index), y=Value,colour=Series),data=fortify(adata,melt=TRUE))
+   g<-g+facet_grid(Series ~ .,scales = "free_y")
+   g<-g+scale_y_continuous(labels = dollar)
+   g<-g+scale_x_date(labels=date_format("%Y-%m"),breaks=date_breaks("2 months"),limits = c(sDate,eDate))
+   g<-g+xlab("") + ylab("Price")+ggtitle(title)
+   g
+ }

# 现金流量
> adata<-as.xts(result1$ticks[which(result1$ticks$op=='S'),]['cash'])
> drawCash(ldata,adata)

line1_3

我们把股价和现金流量并排放置，从2010-09开始均线策略开始大幅赚钱，到2011-10到达最高点，并且超过了本金，然后开始下滑，直截到2012-01亏损3859.86元。这是由于我们把赚到利润继续投资，增大了头寸，以至于2011年底的震荡市让模型失效，从而赔了更多的钱。

这样就完成一条20日均线的交易策略模型，并用IBM的股票做了测试。

3.5 二条均线的交易策略

一条均线模型，在大的趋势下是可以稳定赚钱的，但由于一条均线对于波动非常敏感性，如果小波动过于频繁，不仅会增加交易次数，而且会让模型失效。然后，就有二条均线的策略模型，可以减低对波动的敏感性。

二条均线策略模型，与一条均线模型思路类似，以5日均线价格替换股价，是通过5日均线和20日均线交叉来进行信号交易的。

我们首先画出股价，5日均线和20日均线图。


> ldata<-ma(cdata,c(5,20))  #选择滑动平均指标
> drawLine(ldata,title,sDate,eDate) #画图

line2_1

以散点覆盖20日均线，红色点为买入持有，紫色点为卖出空仓。


# 散点数据
> pdata<-genPoint(pdata,ldata)
> head(pdata)
       Index Series    Value
1 2010-01-04   down 128.7955
2 2010-01-05   down 128.7955
3 2010-01-06   down 128.7955
4 2010-01-07   down 128.7955
5 2010-01-08   down 128.7955
6 2010-01-11   down 128.7955
> drawPoint(ldata,pdata,title,sDate,eDate) #画图

line2_2

用5日均线和20日均线价格做比较，把5日大于均线的部分用紫色表示，股价小于均线的部分用红色表示。我们看到图中，紫色点和红色点在20日均线上交替出现，同样地，我们可以在每次红色出现的第一个点买入股票，然后在紫色的第一个点卖出股票，直观看上去的与一条均线模型类似，都是赚钱的。

我们要找出这些交易信号点，做量化的统计，看看到底能不能赚钱。


> tdata<-Signal(cdata,pdata)
> tdata<-tdata[which(as.Date(row.names(tdata)) head(tdata)
            Value op
2010-01-04 132.45  B
2010-01-26 125.75  S
2010-02-18 127.81  B
2010-03-10 125.62  S
2010-03-16 128.67  B
2010-04-12 128.36  S

# 交易记录
> nrow(tdata)
[1] 36

一共有36条交易记录，买卖各占一半，比一条均线模型少了36笔交易。

利用交易信号数据，进行模拟交易。我们设定交易参数，以$10W为本金，满仓买入或卖出，手续为0，传入交易信号。


#模拟交易
> result2<-trade(tdata,100000)

# 查看每笔交易
> head(result2$ticks)
            Value op     cash amount     asset     diff
2010-01-04 132.45  B     0.25    755 100000.00     0.00
2010-01-26 125.75  S 94941.50      0  94941.50 -5058.50
2010-02-18 127.81  B   106.48    742  94941.50     0.00
2010-03-10 125.62  S 93316.52      0  93316.52 -1624.98
2010-03-16 128.67  B    30.77    725  93316.52     0.00
2010-04-12 128.36  S 93091.77      0  93091.77  -224.75

# 盈利的交易
> head(result2$rise)
            Value op      cash amount     asset     diff
2010-09-10 127.99  B     75.34    649  83140.85     0.00
2010-11-18 144.36  S  93764.98      0  93764.98 10624.13
2010-12-07 144.02  B      2.66    638  91887.42     0.00
2011-02-23 160.18  S 102197.50      0 102197.50 10310.08
2011-03-28 161.37  B    124.70    582  94042.04     0.00
2011-05-20 170.16  S  99157.82      0  99157.82  5115.78

# 亏损的交易
> head(result2$fall)
            Value op     cash amount     asset     diff
2010-01-04 132.45  B     0.25    755 100000.00     0.00
2010-01-26 125.75  S 94941.50      0  94941.50 -5058.50
2010-02-18 127.81  B   106.48    742  94941.50     0.00
2010-03-10 125.62  S 93316.52      0  93316.52 -1624.98
2010-03-16 128.67  B    30.77    725  93316.52     0.00
2010-04-12 128.36  S 93091.77      0  93091.77  -224.75

通过模拟交易，我们精确地算出每笔交易的盈利情况了,有26笔交易是亏损的，16笔交易是有盈利的。

查看最后的资金情况。


> tail(result2$ticks,1)
            Value op    cash amount   asset     diff
2011-12-19 182.89  S 96828.9      0 96828.9 -3581.33

最后，资金剩余96828.9元，亏了3171.1元。

查看资金曲线。


> adata<-as.xts(result2$ticks[which(result2$ticks$op=='S'),]['cash'])
> drawCash(ldata,adata)

line2_3

我们可以发现，虽然最后资金也是赔了3171.1，比一条均线策略模型赔的小一点，但二条均线策略模型有3次高于本金的情况，而且最差的情况也比一条均线最差的情况要好。

3.6 对比两个模型的盈利情况

我们再进一步对比两个模型的盈利情况，找出两个模型中所有赚钱的交易。


# 盈利的交易
> rise<-merge(as.xts(result1$rise[1]),as.xts(result2$rise[1]))
> names(rise)<-c("plan1","plan2")

# 查看数据情况
> rise
            plan1  plan2
2010-03-11 127.60     NA
2010-04-08 127.61     NA
2010-07-22 127.47     NA
2010-08-12 128.30     NA
2010-09-09 126.36     NA
2010-09-10     NA 127.99
2010-11-16 142.24     NA
2010-11-18     NA 144.36
2010-12-07     NA 144.02
2010-12-08 144.98     NA
2011-02-22 161.95     NA
2011-02-23     NA 160.18
2011-03-25 162.18     NA
2011-03-28     NA 161.37
2011-05-16 168.86     NA
2011-05-20     NA 170.16
2011-06-21 166.22     NA
2011-06-23     NA 166.12
2011-08-02 178.05     NA
2011-08-04     NA 171.48
2011-09-14 167.24     NA
2011-09-16     NA 172.99
2011-09-22 168.62     NA
2011-09-23 169.34     NA
2011-10-18 178.90     NA
2011-10-21     NA 181.63

plan1是一条均线模型，plan2是二条均线模型。plan1比plan2多了6次交易，显然多的这几次交易是由于对波动敏感性引起的，反而减少了趋势行情收益。

最后，我们画一下盈利部分的交易区间


> # 均线图+交易区间
> drawRange<-function(ldata,plan,titie="Stock_2014",sDate=min(index(ldata)),eDate=max(index(ldata)),out=FALSE){
+   g<-ggplot(aes(x=Index, y=Value),data=fortify(ldata[,1],melt=TRUE))
+   g<-g+geom_line()
+   g<-g+geom_line(aes(colour=Series),data=fortify(ldata[,-1],melt=TRUE))
+   g<-g+geom_rect(aes(NULL, NULL,xmin=start,xmax=end,fill=plan),ymin = yrng[1], ymax = yrng[2],data=plan)
+   g<-g+scale_fill_manual(values =alpha(c("blue", "red"), 0.2))
+   g<-g+scale_x_date(labels=date_format("%Y-%m"),breaks=date_breaks("2 months"),limits = c(sDate,eDate))
+   g<-g+xlab("") + ylab("Price")+ggtitle(title)
+   
+   if(out) ggsave(g,file=paste(titie,".png",sep=""))
+   else g
+ }

#盈利区间
> plan<-comPlan(ldata,result1,result2){} # 代码省略
> drawRange(ldata,plan,title,sDate,eDate) #画图

plan1的盈利区间。
line3_1

plan1和plan2同时存在的盈利区间。
line3_2

从盈利区间我们可以看到，印证一条均线对波动敏感性的问题，二条均线模型是对一条均线模型的优化，这样我们就一个完整均线模型的实例研发。

3.7 模型优化

如果从交易的角度讲，上面的模型还不能算完成，因为还有很多的赔钱交易，要进行更多地优化，减少最大回撤，在更确定的时机做多，反向做空等。模型优化的问题，会在后面的文章中再进行详细的介绍。

看起来均线模型是如此的简单，但实盘交易时真能在趋势行情中跑赢双均线(优化)模型，也真不是一件容易的事情。二条均线打天下，不说东方不败，也是独孤求败。

######################################################
看文字不过瘾，作者视频讲解，请访问网站：http://onbook.me/video
######################################################

转载请注明出处：
http://blog.fens.me/finance-stock-ma/

打赏作者