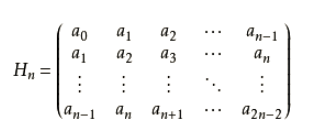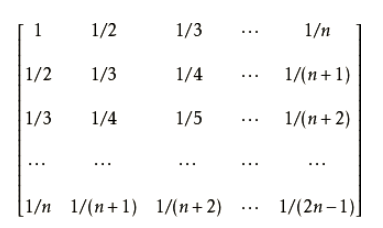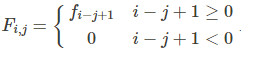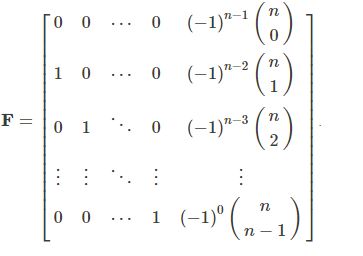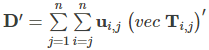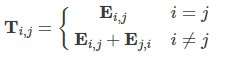Blog Archives

Posted:

Jul 16, 2019

Tags:

Comments:

R语言中的矩阵计算

R的极客理想系列文章，涵盖了R的思想，使用，工具，创新等的一系列要点，以我个人的学习和体验去诠释R的强大。

R语言作为统计学一门语言，一直在小众领域闪耀着光芒。直到大数据的爆发，R语言变成了一门炙手可热的数据分析的利器。随着越来越多的工程背景的人的加入，R语言的社区在迅速扩大成长。现在已不仅仅是统计领域，教育，银行，电商，互联网….都在使用R语言。

要成为有理想的极客，我们不能停留在语法上，要掌握牢固的数学，概率，统计知识，同时还要有创新精神，把R语言发挥到各个领域。让我们一起动起来吧，开始R的极客理想。

关于作者：

张丹(Conan), 程序员/Quant: Java,R,Nodejs
blog: http://blog.fens.me
email: bsspirit@gmail.com

转载请注明出处：
http://blog.fens.me/r-matrix

前言

R是作为统计语言，生来就对数学有良好的支持。矩阵计算作为底层的数学工具，有非常广泛的使用场景。用R语言很好地封装了，矩阵的各种计算方法，一个函数一行代码，就能完成复杂的矩阵分解等操作。让建模人员可以更专注于模型推理和业务逻辑实现，把复杂的矩阵计算交给R语言来完成。

本文总结了R语言用于矩阵的各种计算操作。

基本操作
矩阵计算
矩阵性质
矩阵分解
特殊矩阵

1. 基本操作

生成一个矩阵，计算行、列。


# 生成矩阵 
> m<-matrix(1:20,4,5);m
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    5    9   13   17
[2,]    2    6   10   14   18
[3,]    3    7   11   15   19
[4,]    4    8   12   16   20

# 矩阵行
> nrow(m)
[1] 4
# 矩阵列
> ncol(m)
[1] 5

取对角线元素，生成对角矩阵，


# 对角线元素
> diag(m)
[1]  1  6 11 16

# 以对角线元素，生成对角矩阵
> diag(diag(m))
     [,1] [,2] [,3] [,4]
[1,]    1    0    0    0
[2,]    0    6    0    0
[3,]    0    0   11    0
[4,]    0    0    0   16

上三角，下三角


# 上三角
> m<-matrix(1:20,4,5)
> upper.tri(m)
      [,1]  [,2]  [,3]  [,4] [,5]
[1,] FALSE  TRUE  TRUE  TRUE TRUE
[2,] FALSE FALSE  TRUE  TRUE TRUE
[3,] FALSE FALSE FALSE  TRUE TRUE
[4,] FALSE FALSE FALSE FALSE TRUE

# 上三角值
> m[which(upper.tri(m))] 
 [1]  5  9 10 13 14 15 17 18 19 20

# 上三角矩阵
> m[!upper.tri(m)]<-0;m
     [,1] [,2] [,3] [,4] [,5]
[1,]    0    5    9   13   17
[2,]    0    0   10   14   18
[3,]    0    0    0   15   19
[4,]    0    0    0    0   20

# 下三角矩阵
> m[!lower.tri(m)]<-0;m
     [,1] [,2] [,3] [,4] [,5]
[1,]    0    0    0    0    0
[2,]    2    0    0    0    0
[3,]    3    7    0    0    0
[4,]    4    8   12    0    0

矩阵转置


> m<-matrix(1:20,4,5);m
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    5    9   13   17
[2,]    2    6   10   14   18
[3,]    3    7   11   15   19
[4,]    4    8   12   16   20

# 转置，行列互转
> t(m)
     [,1] [,2] [,3] [,4]
[1,]    1    2    3    4
[2,]    5    6    7    8
[3,]    9   10   11   12
[4,]   13   14   15   16
[5,]   17   18   19   20

对角矩阵填充

# 创建方阵
> m<-matrix(1:16,4,4);m
     [,1] [,2] [,3] [,4]
[1,]    1    5    9   13
[2,]    2    6   10   14
[3,]    3    7   11   15
[4,]    4    8   12   16

# 用上三角填充下三角
> m[lower.tri(m)]<-m[upper.tri(m)]
> m
     [,1] [,2] [,3] [,4]
[1,]    1    5    9   13
[2,]    5    6   10   14
[3,]    9   13   11   15
[4,]   10   14   15   16

填充后，发现矩阵并不是对称的，原因是上三角取值按列取值，所以先取10后取13，导致上三角和下三角取值顺序不完全一致。


> m<-matrix(1:16,4,4);m
     [,1] [,2] [,3] [,4]
[1,]    1    5    9   13
[2,]    2    6   10   14
[3,]    3    7   11   15
[4,]    4    8   12   16

# 上三角取值
> m[upper.tri(m)]
[1]  5  9 10 13 14 15

# 下三角取值
> m[lower.tri(m)]
[1]  2  3  4  7  8 12

调整后，我们要先转置，再取值再填充，形成对称结构。


> m<-matrix(1:20,4,5)

# 转置后，取下三角，填充下三角
> m[lower.tri(m)]<-t(m)[lower.tri(m)]
> m
     [,1] [,2] [,3] [,4]
[1,]    1    5    9   13
[2,]    5    6   10   14
[3,]    9   10   11   15
[4,]   13   14   15   16

矩阵和data.frame转换，用行列形成索引结构


> m<-matrix(1:12,4,3);m
     [,1] [,2] [,3]
[1,]    1    5    9
[2,]    2    6   10
[3,]    3    7   11
[4,]    4    8   12

# 矩阵转行列data.frame
> row<-rep(1:nrow(m),ncol(m))              # 行
> col<-rep(1:ncol(m),each=nrow(m))         # 列
> df<-data.frame(row,col,v=as.numeric(m))  # 行列索引数据框
> df
   row col  v
1    1   1  1
2    2   1  2
3    3   1  3
4    4   1  4
5    1   2  5
6    2   2  6
7    3   2  7
8    4   2  8
9    1   3  9
10   2   3 10
11   3   3 11
12   4   3 12

# 行列索引数据框转矩阵
> m<-matrix(0,length(unique(df$row)),length(unique(df$col)) )
> apply(df,1,function(dat){
+     m[dat[1],dat[2]]<<-dat[3]  
+     invisible()
+ })
# 打印矩阵
> m
     [,1] [,2] [,3]
[1,]    1    5    9
[2,]    2    6   10
[3,]    3    7   11
[4,]    4    8   12

2. 矩阵计算

加法，减法


# 加载矩阵计算工具包
> library(matrixcalc)

# 新建2个矩阵，行列长度相同
> m0<-matrix(1:20,4,5);m0
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    5    9   13   17
[2,]    2    6   10   14   18
[3,]    3    7   11   15   19
[4,]    4    8   12   16   20
> m1<-matrix(sample(100,20),4,5);m1
     [,1] [,2] [,3] [,4] [,5]
[1,]   40   79   97   57   78
[2,]   93   32   48    8   95
[3,]   63    6   56   12    9
[4,]   28   31   72   27   26

# 矩阵加法
> m0+m1
     [,1] [,2] [,3] [,4] [,5]
[1,]   41   84  106   70   95
[2,]   95   38   58   22  113
[3,]   66   13   67   27   28
[4,]   32   39   84   43   46

# 矩阵减法
> m0-m1
     [,1] [,2] [,3] [,4] [,5]
[1,]  -39  -74  -88  -44  -61
[2,]  -91  -26  -38    6  -77
[3,]  -60    1  -45    3   10
[4,]  -24  -23  -60  -11   -6

矩阵值相乘


> m0*m1
     [,1] [,2] [,3] [,4] [,5]
[1,]   40  395  873  741 1326
[2,]  186  192  480  112 1710
[3,]  189   42  616  180  171
[4,]  112  248  864  432  520

矩阵乘法，满足第二个矩阵的列数和第一个矩阵的行数相等，所以把上面生成的m0矩阵(4行5列)转置为(5行4列)，再用m1矩阵(4行5列)，进行矩阵乘法，得到一个5行5列的结果矩阵。


> t(m0)%*%m1
     [,1] [,2] [,3] [,4] [,5]
[1,]  527  285  649  217  399
[2,] 1423  877 1741  633 1231
[3,] 2319 1469 2833 1049 2063
[4,] 3215 2061 3925 1465 2895
[5,] 4111 2653 5017 1881 3727

# 通过函数实现矩阵相乘
> crossprod(m0,m1)
     [,1] [,2] [,3] [,4] [,5]
[1,]  527  285  649  217  399
[2,] 1423  877 1741  633 1231
[3,] 2319 1469 2833 1049 2063
[4,] 3215 2061 3925 1465 2895
[5,] 4111 2653 5017 1881 3727

矩阵外积


> m<-matrix(1:6,2);m
     [,1] [,2] [,3]
[1,]    1    3    5
[2,]    2    4    6
> t(m)
     [,1] [,2]
[1,]    1    2
[2,]    3    4
[3,]    5    6

> m %o% t(m)  # 外积，同outer(m,t(m))
, , 1, 1

     [,1] [,2] [,3]
[1,]    1    3    5
[2,]    2    4    6

, , 2, 1

     [,1] [,2] [,3]
[1,]    3    9   15
[2,]    6   12   18

, , 3, 1

     [,1] [,2] [,3]
[1,]    5   15   25
[2,]   10   20   30

, , 1, 2

     [,1] [,2] [,3]
[1,]    2    6   10
[2,]    4    8   12

, , 2, 2

     [,1] [,2] [,3]
[1,]    4   12   20
[2,]    8   16   24

, , 3, 2

     [,1] [,2] [,3]
[1,]    6   18   30
[2,]   12   24   36

矩阵直和


> m0<-matrix(1:4,2,2);m0
     [,1] [,2]
[1,]    1    3
[2,]    2    4
> m1<-matrix(1:9,3,3);m1
     [,1] [,2] [,3]
[1,]    1    4    7
[2,]    2    5    8
[3,]    3    6    9

> m0 %s% m1       #矩阵直和，同 direct.sum(m0,m1) 
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    3    0    0    0
[2,]    2    4    0    0    0
[3,]    0    0    1    4    7
[4,]    0    0    2    5    8
[5,]    0    0    3    6    9

矩阵直积


> m0<-matrix(1:4,2,2);m0
     [,1] [,2]
[1,]    1    3
[2,]    2    4
> m1<-matrix(1:9,3,3);m1
     [,1] [,2] [,3]
[1,]    1    4    7
[2,]    2    5    8
[3,]    3    6    9

> m0 %x% m1     #矩阵直积，同 kronecker(m0,m1)，direct.prod(m0,m1)
     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]    1    4    7    3   12   21
[2,]    2    5    8    6   15   24
[3,]    3    6    9    9   18   27
[4,]    2    8   14    4   16   28
[5,]    4   10   16    8   20   32
[6,]    6   12   18   12   24   36

3. 矩阵性质

3.1 奇异矩阵
首先，我们线创建一个非奇异矩阵，判断非奇异矩阵方法，行列式不等于0，矩阵可逆，满秩。


# 创建一个非奇异矩阵
> m1<-matrix(sample(1:16),4)

# 行列式不等于0
> det(m1)     # !=0
[1] 14193

# 有逆矩阵
> solve(m1)   # 可逆
             [,1]        [,2]        [,3]         [,4]
[1,] -0.026210104  0.09666737  0.02473050 -0.119988727
[2,] -0.002325090  0.08384415 -0.07038681  0.008173043
[3,] -0.007186641 -0.13478475  0.05516804  0.176777285
[4,]  0.074614246  0.03663778 -0.01395054 -0.080462200

# 满秩
> library(matrixcalc)
> matrix.rank(m1)    # 长度=n,满秩
[1] 4

再创建一个奇异矩阵，判断奇异矩阵方法包括，行列式等于0，矩阵不可逆，不是满秩。


# 奇异矩阵
> m0<-matrix(1:16,4)

# 计算行列式
> det(m0)     
[1] 0

# 不可逆
> solve(m0)   
Error in solve.default(m0) : 
  Lapack routine dgesv: system is exactly singular: U[3,3] = 0

# 不是满秩
> matrix.rank(m0)     # 长度<4
[1] 2

3.2 逆矩阵


# 创建方阵，非奇异矩阵
> m0<-matrix(sample(100,16),4,4);m0
     [,1] [,2] [,3] [,4]
[1,]   24   31   80   37
[2,]   84   13   42   71
[3,]   95   62   93   86
[4,]   69   16   94   35

# 计算矩阵的逆矩阵
> solve(m0)
            [,1]          [,2]        [,3]         [,4]
[1,] -0.03083680 -0.0076561475  0.01258023  0.017218514
[2,] -0.01710957 -0.0270246488  0.03152548 -0.004553923
[3,]  0.01384721 -0.0003070371 -0.00886117  0.007757524
[4,]  0.03142440  0.0282722871 -0.01541411 -0.024126340

# 逆矩阵的性质，逆矩阵与原矩阵进行矩阵乘法，得到对角矩阵。
> round(solve(m0) %*% m0)  # 对角矩阵
     [,1] [,2] [,3] [,4]
[1,]    1    0    0    0
[2,]    0    1    0    0
[3,]    0    0    1    0
[4,]    0    0    0    1

广义逆矩阵，将逆矩阵的概率推广到奇异矩阵和长方形矩阵上，就产生了广义逆矩阵。


# 创建奇异矩阵
> m<-matrix(1:16,4,4);m 
     [,1] [,2] [,3] [,4]
[1,]    1    5    9   13
[2,]    2    6   10   14
[3,]    3    7   11   15
[4,]    4    8   12   16

# 逆矩阵计算失败
> solve(m)
Error in solve.default(m) : 
  Lapack routine dgesv: system is exactly singular: U[3,3] = 0

# 广义逆矩阵
> library(MASS) # 加载MASS包
> ginv(m)
       [,1]    [,2]  [,3]    [,4]
[1,] -0.285 -0.1075  0.07  0.2475
[2,] -0.145 -0.0525  0.04  0.1325
[3,] -0.005  0.0025  0.01  0.0175
[4,]  0.135  0.0575 -0.02 -0.0975

用ginv函数计算非奇异矩阵，和solve()函数比较。


# 非奇异矩阵
> m0<-matrix(sample(100,16),4,4);m0
     [,1] [,2] [,3] [,4]
[1,]    5   61   75   74
[2,]   10   67   11   21
[3,]   29   32   92   17
[4,]   72   23   87   36

# 计算广义矩阵的逆矩阵，与solve()结果相同
> ginv(m0)
              [,1]         [,2]         [,3]         [,4]
[1,] -0.0080590817  0.006534814 -0.011333076  0.018105645
[2,] -0.0041284695  0.017615769  0.005333304 -0.004308072
[3,]  0.0009226026 -0.006671759  0.016312821 -0.005707878
[4,]  0.0165261737 -0.008200731 -0.020163889  0.008112906

# 计算矩阵的逆矩阵
> solve(m0)
              [,1]         [,2]         [,3]         [,4]
[1,] -0.0080590817  0.006534814 -0.011333076  0.018105645
[2,] -0.0041284695  0.017615769  0.005333304 -0.004308072
[3,]  0.0009226026 -0.006671759  0.016312821 -0.005707878
[4,]  0.0165261737 -0.008200731 -0.020163889  0.008112906

逆矩阵的特性


> m<-matrix(1:16,4,4);m 
     [,1] [,2] [,3] [,4]
[1,]    1    5    9   13
[2,]    2    6   10   14
[3,]    3    7   11   15
[4,]    4    8   12   16

# 原矩阵%*%广义逆矩阵%*%原矩阵=原矩阵
> m %*% ginv(m) %*% m 
     [,1] [,2] [,3] [,4]
[1,]    1    5    9   13
[2,]    2    6   10   14
[3,]    3    7   11   15
[4,]    4    8   12   16

# 广义逆矩阵%*%原矩阵%*%广义逆矩阵=广义逆矩阵
> ginv(m) %*% m %*% ginv(m) 
       [,1]    [,2]  [,3]    [,4]
[1,] -0.285 -0.1075  0.07  0.2475
[2,] -0.145 -0.0525  0.04  0.1325
[3,] -0.005  0.0025  0.01  0.0175
[4,]  0.135  0.0575 -0.02 -0.0975

# 原矩阵%*%广义逆矩阵=转置后的，原矩阵%*%广义逆矩阵
> m %*% ginv(m)    
     [,1] [,2] [,3] [,4]
[1,]  0.7  0.4  0.1 -0.2
[2,]  0.4  0.3  0.2  0.1
[3,]  0.1  0.2  0.3  0.4
[4,] -0.2  0.1  0.4  0.7
> t(m %*% ginv(m)) 
     [,1] [,2] [,3] [,4]
[1,]  0.7  0.4  0.1 -0.2
[2,]  0.4  0.3  0.2  0.1
[3,]  0.1  0.2  0.3  0.4
[4,] -0.2  0.1  0.4  0.7

# 广义逆矩阵%*%原矩阵=转置后的，广义逆矩阵%*%原矩阵
> ginv(m) %*% m   
     [,1] [,2] [,3] [,4]
[1,]  0.7  0.4  0.1 -0.2
[2,]  0.4  0.3  0.2  0.1
[3,]  0.1  0.2  0.3  0.4
[4,] -0.2  0.1  0.4  0.7
> t(ginv(m) %*% m)
     [,1] [,2] [,3] [,4]
[1,]  0.7  0.4  0.1 -0.2
[2,]  0.4  0.3  0.2  0.1
[3,]  0.1  0.2  0.3  0.4
[4,] -0.2  0.1  0.4  0.7

3.3 特征值和特征向量


# 创建一个方阵
> m0<-matrix(sample(100,16),4,4);m0
     [,1] [,2] [,3] [,4]
[1,]   97   93   11   70
[2,]   19   58   23   90
[3,]   17   94    6   35
[4,]   79   71   43   88

# 计算特征值和特征向量
> eigen(m0)
eigen() decomposition
$values
[1] 236.14449+ 0.00000i  40.51501+ 0.00000i -13.82975+32.81166i -13.82975-32.81166i

$vectors
             [,1]          [,2]                  [,3]                  [,4]
[1,] 0.6055193+0i -0.6428709+0i  0.2114869-0.0613776i  0.2114869+0.0613776i
[2,] 0.4115920+0i  0.3939259+0i -0.0781518+0.3993580i -0.0781518-0.3993580i
[3,] 0.3054253+0i  0.6482306+0i  0.7557355+0.0000000i  0.7557355+0.0000000i
[4,] 0.6088134+0i -0.1064728+0i -0.3210016-0.3342655i -0.3210016+0.3342655i

当symmetric=TRUE时，计算对称矩阵的特征值和特征向量，当m0不是对称矩阵时，则取下三角对称结构进行计算。


> eigen(m0,symmetric = TRUE)
eigen() decomposition
$values
[1] 231.824838  87.176816  -3.422899 -66.578756

$vectors
           [,1]       [,2]       [,3]        [,4]
[1,] -0.4801643  0.7155875  0.5040624 -0.05742733
[2,] -0.5024315 -0.5470752  0.2262475 -0.63014551
[3,] -0.3634220 -0.4138943  0.3287896  0.76714627
[4,] -0.6204267  0.1316618 -0.7659181  0.10538188

# 生成下三角矩阵的对称矩阵
> m0[upper.tri(m0)]<-t(m0)[upper.tri(m0)];m0
     [,1] [,2] [,3] [,4]
[1,]   97   19   17   79
[2,]   19   58   94   71
[3,]   17   94    6   43
[4,]   79   71   43   88

# 计算特征值，与eigen(m0,symmetric = TRUE) 一致
> eigen(m0)
eigen() decomposition
$values
[1] 231.824838  87.176816  -3.422899 -66.578756

$vectors
           [,1]       [,2]       [,3]        [,4]
[1,] -0.4801643  0.7155875  0.5040624 -0.05742733
[2,] -0.5024315 -0.5470752  0.2262475 -0.63014551
[3,] -0.3634220 -0.4138943  0.3287896  0.76714627
[4,] -0.6204267  0.1316618 -0.7659181  0.10538188

4. 矩阵分解

下面将介绍4种矩阵常用的分解的方法，包括三解分解LU，choleskey分解，QR分解，奇异值分解SVD。

4.1 三解分解LU
三角分解法是将原方阵分解成一个上三角形矩阵和一个下三角形矩阵，这样的分解法又称为LU分解法。它的用途主要在简化一个大矩阵的行列式值的计算过程，求逆矩阵，和求解联立方程组。这种分解法所得到的上下三角形矩阵不唯一，一对上三角形矩阵和下三角形矩阵，矩阵相乘会得到原矩阵。


创建一个矩阵
> m0<-matrix(sample(100,16),4);m0
     [,1] [,2] [,3] [,4]
[1,]   25   88   35   87
[2,]   26   75   73   15
[3,]   36   62   80   53
[4,]   70   44   21   47

# 三角分解
> lu<-lu.decomposition(m0)
> lu
$L                                        # 下三角矩阵
     [,1]      [,2]     [,3] [,4]
[1,] 1.00  0.000000 0.000000    0
[2,] 1.04  1.000000 0.000000    0
[3,] 1.44  3.917676 1.000000    0
[4,] 2.80 12.251816 4.617547    1

$U                                        # 上三角矩阵
     [,1]   [,2]      [,3]      [,4]
[1,]   25  88.00   35.0000   87.0000
[2,]    0 -16.52   36.6000  -75.4800
[3,]    0   0.00 -113.7869  223.4262
[4,]    0   0.00    0.0000 -303.5137

# 三角分解的下三角矩阵L %*% 三角分解的上三角矩阵U = 原矩阵
> lu$L %*% lu$U
     [,1] [,2] [,3] [,4]
[1,]   25   88   35   87
[2,]   26   75   73   15
[3,]   36   62   80   53
[4,]   70   44   21   47

4.2 choleskey分解
Cholesky 分解是把一个对称正定的矩阵表示成一个下三角矩阵L和其转置的乘积的分解。它要求矩阵的所有特征值必须大于零，故分解的下三角的对角元也是大于零的。Cholesky分解法又称平方根法，是当A为实对称正定矩阵时，LU三角分解法的变形。


创建对称方阵
> m1<-diag(5)+2;m1
     [,1] [,2] [,3] [,4] [,5]
[1,]    3    2    2    2    2
[2,]    2    3    2    2    2
[3,]    2    2    3    2    2
[4,]    2    2    2    3    2
[5,]    2    2    2    2    3

# choleskey分解
> chol(m1)
         [,1]     [,2]      [,3]      [,4]      [,5]
[1,] 1.732051 1.154701 1.1547005 1.1547005 1.1547005
[2,] 0.000000 1.290994 0.5163978 0.5163978 0.5163978
[3,] 0.000000 0.000000 1.1832160 0.3380617 0.3380617
[4,] 0.000000 0.000000 0.0000000 1.1338934 0.2519763
[5,] 0.000000 0.000000 0.0000000 0.0000000 1.1055416

# choleskey分解的性质
# chol分解的逆矩阵 %*% chol分解矩阵 = 原矩阵
> t(chol(m1))%*%chol(m1)
     [,1] [,2] [,3] [,4] [,5]
[1,]    3    2    2    2    2
[2,]    2    3    2    2    2
[3,]    2    2    3    2    2
[4,]    2    2    2    3    2
[5,]    2    2    2    2    3

# chol分解矩阵的对角线值的平方的积 = 行列式的模数
> prod(diag(chol(m1))^2)
[1] 11
> det(m1)
[1] 11

# chol分解的逆
> chol2inv(m1)
             [,1]         [,2]        [,3]         [,4]         [,5]
[1,]  0.166658199 -0.055580958 -0.01859473 -0.006401463 -0.002743484
[2,] -0.055580958  0.166590459 -0.05578418 -0.019204390 -0.008230453
[3,] -0.018594726 -0.055784179  0.16598080 -0.057613169 -0.024691358
[4,] -0.006401463 -0.019204390 -0.05761317  0.160493827 -0.074074074
[5,] -0.002743484 -0.008230453 -0.02469136 -0.074074074  0.111111111

> chol2inv(chol(m1))
           [,1]       [,2]       [,3]       [,4]       [,5]
[1,]  0.8181818 -0.1818182 -0.1818182 -0.1818182 -0.1818182
[2,] -0.1818182  0.8181818 -0.1818182 -0.1818182 -0.1818182
[3,] -0.1818182 -0.1818182  0.8181818 -0.1818182 -0.1818182
[4,] -0.1818182 -0.1818182 -0.1818182  0.8181818 -0.1818182
[5,] -0.1818182 -0.1818182 -0.1818182 -0.1818182  0.8181818

4.3 QR分解
QR分解法是将矩阵分解成一个正规正交矩阵与上三角形矩阵,所以称为QR分解法,与此正规正交矩阵的通用符号Q有关。


# 创建对称方阵
> m1<-diag(5)+2;m1
     [,1] [,2] [,3] [,4] [,5]
[1,]    3    2    2    2    2
[2,]    2    3    2    2    2
[3,]    2    2    3    2    2
[4,]    2    2    2    3    2
[5,]    2    2    2    2    3

# QR分解
> q<-qr(m1);q
$qr
     [,1]       [,2]       [,3]       [,4]       [,5]
[1,] -5.0 -4.8000000 -4.8000000 -4.8000000 -4.8000000
[2,]  0.4 -1.4000000 -0.6857143 -0.6857143 -0.6857143
[3,]  0.4  0.2142857 -1.2205720 -0.4012839 -0.4012839
[4,]  0.4  0.2142857  0.1560549 -1.1527216 -0.2852095
[5,]  0.4  0.2142857  0.1560549  0.1246843  1.1168808

$rank
[1] 5

$qraux
[1] 1.600000 1.928571 1.975343 1.992196 1.116881

$pivot
[1] 1 2 3 4 5

attr(,"class")
[1] "qr"

# 计算QR分解矩阵的R值
> qr.R(q)
     [,1] [,2]       [,3]       [,4]       [,5]
[1,]   -5 -4.8 -4.8000000 -4.8000000 -4.8000000
[2,]    0 -1.4 -0.6857143 -0.6857143 -0.6857143
[3,]    0  0.0 -1.2205720 -0.4012839 -0.4012839
[4,]    0  0.0  0.0000000 -1.1527216 -0.2852095
[5,]    0  0.0  0.0000000  0.0000000  1.1168808

# 计算QR分解矩阵的Q值
> qr.Q(q)
     [,1]        [,2]        [,3]        [,4]       [,5]
[1,] -0.6  0.62857143  0.36784361  0.26144202 -0.2030692
[2,] -0.4 -0.77142857  0.36784361  0.26144202 -0.2030692
[3,] -0.4 -0.05714286 -0.85272836  0.26144202 -0.2030692
[4,] -0.4 -0.05714286 -0.03344033 -0.89127960 -0.2030692
[5,] -0.4 -0.05714286 -0.03344033 -0.02376746  0.9138115

# QR分解的性质
# Q的值 %*% R值 = 原矩阵
> qr.Q(q) %*% qr.R(q) #=m1
     [,1] [,2] [,3] [,4] [,5]
[1,]    3    2    2    2    2
[2,]    2    3    2    2    2
[3,]    2    2    3    2    2
[4,]    2    2    2    3    2
[5,]    2    2    2    2    3

# X值 = 原矩阵，同Q的值 %*% R值 
> qr.X(q) #=m1
     [,1] [,2] [,3] [,4] [,5]
[1,]    3    2    2    2    2
[2,]    2    3    2    2    2
[3,]    2    2    3    2    2
[4,]    2    2    2    3    2
[5,]    2    2    2    2    3

# Q值的转置矩阵 * Q值 = 
> t(qr.Q(q)) %*% qr.Q(q)
              [,1]          [,2]          [,3]         [,4]          [,5]
[1,]  1.000000e+00 -3.469447e-17 -2.081668e-17 1.214306e-17  5.551115e-17
[2,] -3.469447e-17  1.000000e+00  7.199102e-17 5.204170e-17 -7.632783e-17
[3,] -2.081668e-17  7.199102e-17  1.000000e+00 3.382711e-17 -6.938894e-18
[4,]  1.214306e-17  5.204170e-17  3.382711e-17 1.000000e+00  3.122502e-17
[5,]  5.551115e-17 -7.632783e-17 -6.938894e-18 3.122502e-17  1.000000e+00

4.4 奇异值分解SVD
奇异值分解 (singular value decomposition, SVD) 是一种正交矩阵分解法。SVD是最可靠的分解法，但是它比QR 分解法要花上近十倍的计算时间。[U,S,V]=svd(A)，其中U和V分别代表两个正交矩阵，而S代表一对角矩阵。和QR分解法相同，原矩阵A不必为正方矩阵。使用SVD分解法的用途是解最小平方误差法和数据压缩。


# 创建对称方阵
> m1<-diag(5)+2;m1
     [,1] [,2] [,3] [,4] [,5]
[1,]    3    2    2    2    2
[2,]    2    3    2    2    2
[3,]    2    2    3    2    2
[4,]    2    2    2    3    2
[5,]    2    2    2    2    3

# 奇异值分解
> s<-svd(m1);s
$d
[1] 11  1  1  1  1

$u
           [,1]          [,2]          [,3]          [,4]       [,5]
[1,] -0.4472136  4.440892e-17 -3.330669e-17 -3.108624e-16  0.8944272
[2,] -0.4472136 -3.219647e-16  2.414735e-16  8.660254e-01 -0.2236068
[3,] -0.4472136 -5.773503e-01  5.773503e-01 -2.886751e-01 -0.2236068
[4,] -0.4472136 -2.113249e-01 -7.886751e-01 -2.886751e-01 -0.2236068
[5,] -0.4472136  7.886751e-01  2.113249e-01 -2.886751e-01 -0.2236068

$v
           [,1]          [,2]          [,3]       [,4]       [,5]
[1,] -0.4472136  0.000000e+00  0.000000e+00  0.0000000  0.8944272
[2,] -0.4472136 -1.665335e-16  1.457168e-16  0.8660254 -0.2236068
[3,] -0.4472136 -5.773503e-01  5.773503e-01 -0.2886751 -0.2236068
[4,] -0.4472136 -2.113249e-01 -7.886751e-01 -0.2886751 -0.2236068
[5,] -0.4472136  7.886751e-01  2.113249e-01 -0.2886751 -0.2236068

# 奇异分解性质
# svd的u矩阵 %*% svd的d矩阵的对角性值 %*% svd的v的转置矩阵 = 原矩阵
> s$u %*% diag(s$d) %*% t(s$v) #=m1
[,1] [,2] [,3] [,4] [,5]
[1,]    3    2    2    2    2
[2,]    2    3    2    2    2
[3,]    2    2    3    2    2
[4,]    2    2    2    3    2
[5,]    2    2    2    2    3

# svd的u矩阵的转置矩阵 %*% svd的u矩阵 = svd的s矩阵的转置矩阵 %*% svd的v矩阵
> t(s$u) %*% s$u
[,1]          [,2]          [,3]          [,4]          [,5]
[1,]  1.000000e+00  0.000000e+00 -5.551115e-17  0.000000e+00 -2.775558e-17
[2,]  0.000000e+00  1.000000e+00 -2.775558e-17 -1.387779e-16  8.326673e-17
[3,] -5.551115e-17 -2.775558e-17  1.000000e+00  6.245005e-17 -6.938894e-17
[4,]  0.000000e+00 -1.387779e-16  6.245005e-17  1.000000e+00 -1.387779e-16
[5,] -2.775558e-17  8.326673e-17 -6.938894e-17 -1.387779e-16  1.000000e+00
> t(s$v) %*% s$v
[,1]          [,2]         [,3]          [,4]          [,5]
[1,]  1.000000e+00  0.000000e+00 5.551115e-17 -1.665335e-16  2.775558e-17
[2,]  0.000000e+00  1.000000e+00 8.326673e-17 -8.326673e-17  0.000000e+00
[3,]  5.551115e-17  8.326673e-17 1.000000e+00  1.595946e-16  2.775558e-17
[4,] -1.665335e-16 -8.326673e-17 1.595946e-16  1.000000e+00 -8.326673e-17
[5,]  2.775558e-17  0.000000e+00 2.775558e-17 -8.326673e-17  1.000000e+00

5. 特殊矩阵

下面介绍的多种特殊矩阵，都是在matrixcalc库中提供的。

5.1 Hankel Matrix
汉克尔矩阵 (Hankel Matrix) 是具有恒定倾斜对角线的方形矩阵。 Hankel矩阵的行列式称为catalecticant。该函数根据n向量x的值构造n阶Hankel矩阵。矩阵的每一行是前一行中值的循环移位。

矩阵定义:


> hankel.matrix(6, 1:50)
     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]    1    2    3    4    5    6
[2,]    2    3    4    5    6    7
[3,]    3    4    5    6    7    8
[4,]    4    5    6    7    8    9
[5,]    5    6    7    8    9   10
[6,]    6    7    8    9   10   11

5.2 Hilbert Matrix
希尔伯特矩阵是一种数学变换矩阵，正定，且高度病态（即，任何一个元素发生一点变动，整个矩阵的行列式的值和逆矩阵都会发生巨大变化），病态程度和阶数相关。希尔伯特矩阵是一种特殊的汉克尔矩阵，该函数返回n乘n希尔伯特矩阵。

矩阵定义:


> hilbert.matrix(4)
          [,1]      [,2]      [,3]      [,4]
[1,] 1.0000000 0.5000000 0.3333333 0.2500000
[2,] 0.5000000 0.3333333 0.2500000 0.2000000
[3,] 0.3333333 0.2500000 0.2000000 0.1666667
[4,] 0.2500000 0.2000000 0.1666667 0.1428571

5.3 Creation Matrix
创造矩阵，n阶创建矩阵也称为推导矩阵，该函数返回阶数n创建矩阵，在主对角线下方的子对角线上具有序列1,2，…，n-1的方阵。

矩阵定义：


> creation.matrix(5)  
     [,1] [,2] [,3] [,4] [,5]
[1,]    0    0    0    0    0
[2,]    1    0    0    0    0
[3,]    0    2    0    0    0
[4,]    0    0    3    0    0
[5,]    0    0    0    4    0

5.4 Stirling Matrix
斯特林公式（Stirling’s approximation）是一条用来取n的阶乘的近似值的数学公式。一般来说，当n很大的时候，n阶乘的计算量十分大，所以斯特林公式十分好用，而且，即使在n很小的时候，斯特林公式的取值已经十分准确。

斯特林矩阵(Stirling Matrix)，该函数构造并返回斯特林矩阵，该矩阵是包含第二类斯特林数的下三角矩阵。

矩阵定义：


> stirling.matrix(4)
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    0    0    0    0
[2,]    0    1    0    0    0
[3,]    0    1    1    0    0
[4,]    0    1    3    1    0
[5,]    0    1    7    6    1

5.5 Pascal matrix
帕斯卡矩阵：由杨辉三角形表组成的矩阵称为帕斯卡(Pascal)矩阵。此函数返回n乘以Pascal矩阵。在数学中，尤其是矩阵理论和组合学，Pascal矩阵是一个下三角矩阵，行中有二项式系数。通过对相同顺序的对称Pascal矩阵执行LU分解并返回下三角矩阵，可以容易地获得它。

帕斯卡的三角形是由数字行组成的三角形。第一行具有条目1.每个后续行通过添加前一行的相邻条目而形成，替换为0，其中不存在相邻条目。 pascal函数通过选择与指定矩阵维度相对应的Pascal三角形部分来形成Pascal矩阵，

矩阵定义：


> pascal.matrix(4)
     [,1] [,2] [,3] [,4]
[1,]    1    0    0    0
[2,]    1    1    0    0
[3,]    1    2    1    0
[4,]    1    3    3    1

5.6 Fibonacci matrix
斐波纳契矩阵，该函数构造了从Fibonacci序列导出的n + 1平方Fibonacci矩阵。

计算公式：


> fibonacci.matrix(4)
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    1    0    0    0
[2,]    2    1    1    0    0
[3,]    3    2    1    1    0
[4,]    5    3    2    1    1
[5,]    8    5    3    2    1

5.7 Frobenius Matrix
Frobenius矩阵也称为伴随矩阵，它出现在线性一阶微分方程组的解中。
此函数返回一个在数值数学中有用的Fronenius矩阵。

矩阵定义：


> frobenius.matrix(4)
     [,1] [,2] [,3] [,4]
[1,]    0    0    0   -1
[2,]    1    0    0    4
[3,]    0    1    0   -6
[4,]    0    0    1    4

5.8 Duplication matrix
复制矩阵，当A是对称矩阵时，该函数构造将vech（A）映射到vec（A）的线性变换D.

计算公式：


> D.matrix(3) 
      [,1] [,2] [,3] [,4] [,5] [,6]
 [1,]    1    0    0    0    0    0
 [2,]    0    1    0    0    0    0
 [3,]    0    0    1    0    0    0
 [4,]    0    1    0    0    0    0
 [5,]    0    0    0    1    0    0
 [6,]    0    0    0    0    1    0
 [7,]    0    0    1    0    0    0
 [8,]    0    0    0    0    1    0
 [9,]    0    0    0    0    0    1

5.9 K matrix
k矩阵是由H.matrices()函数构造的，利用直积进行计算子列表的分量。K.matrix(r, c = r)，返回阶数为p = r * c的方阵，对于r行c列的矩阵A，计算A和t(A)的直积。

计算公式：


> K.matrix(2,3)
     [,1] [,2] [,3] [,4] [,5] [,6]
[1,]    1    0    0    0    0    0
[2,]    0    0    1    0    0    0
[3,]    0    0    0    0    1    0
[4,]    0    1    0    0    0    0
[5,]    0    0    0    1    0    0
[6,]    0    0    0    0    0    1

5.10 E Matrices
E矩阵列表，E.matrices(n)使得每个子列表的分量，是从n阶单位矩阵计算向量的外积导出的方阵。

计算公式：


> E.matrices(3)
[[1]]
[[1]][[1]]
     [,1] [,2] [,3]
[1,]    1    0    0
[2,]    0    0    0
[3,]    0    0    0

[[1]][[2]]
     [,1] [,2] [,3]
[1,]    0    1    0
[2,]    0    0    0
[3,]    0    0    0

[[1]][[3]]
     [,1] [,2] [,3]
[1,]    0    0    1
[2,]    0    0    0
[3,]    0    0    0


[[2]]
[[2]][[1]]
     [,1] [,2] [,3]
[1,]    0    0    0
[2,]    1    0    0
[3,]    0    0    0

[[2]][[2]]
     [,1] [,2] [,3]
[1,]    0    0    0
[2,]    0    1    0
[3,]    0    0    0

[[2]][[3]]
     [,1] [,2] [,3]
[1,]    0    0    0
[2,]    0    0    1
[3,]    0    0    0


[[3]]
[[3]][[1]]
     [,1] [,2] [,3]
[1,]    0    0    0
[2,]    0    0    0
[3,]    1    0    0

[[3]][[2]]
     [,1] [,2] [,3]
[1,]    0    0    0
[2,]    0    0    0
[3,]    0    1    0

[[3]][[3]]
     [,1] [,2] [,3]
[1,]    0    0    0
[2,]    0    0    0
[3,]    0    0    1

5.11 H Matrices
H矩阵列表，H.matrices(r, c = r)使得r阶c阶的子列表的分量，计算从r行和c列的单位矩阵的列向量的外积导出的方阵。


> H.matrices(2,3)
[[1]]
[[1]][[1]]
     [,1] [,2] [,3]
[1,]    1    0    0
[2,]    0    0    0

[[1]][[2]]
     [,1] [,2] [,3]
[1,]    0    1    0
[2,]    0    0    0

[[1]][[3]]
     [,1] [,2] [,3]
[1,]    0    0    1
[2,]    0    0    0


[[2]]
[[2]][[1]]
     [,1] [,2] [,3]
[1,]    0    0    0
[2,]    1    0    0

[[2]][[2]]
     [,1] [,2] [,3]
[1,]    0    0    0
[2,]    0    1    0

[[2]][[3]]
     [,1] [,2] [,3]
[1,]    0    0    0
[2,]    0    0    1

5.12 T Matrices
T矩阵列表，T.matrices(n) 高级别列表中的组件数为n。 n个组件中的每一个也是列表。每个子列表具有n个分量，每个分量是n阶矩阵。

计算公式：


> T.matrices(3)
[[1]]
[[1]][[1]]
     [,1] [,2] [,3]
[1,]    1    0    0
[2,]    0    0    0
[3,]    0    0    0

[[1]][[2]]
     [,1] [,2] [,3]
[1,]    0    1    0
[2,]    1    0    0
[3,]    0    0    0

[[1]][[3]]
     [,1] [,2] [,3]
[1,]    0    0    1
[2,]    0    0    0
[3,]    1    0    0


[[2]]
[[2]][[1]]
     [,1] [,2] [,3]
[1,]    0    1    0
[2,]    1    0    0
[3,]    0    0    0

[[2]][[2]]
     [,1] [,2] [,3]
[1,]    0    0    0
[2,]    0    1    0
[3,]    0    0    0

[[2]][[3]]
     [,1] [,2] [,3]
[1,]    0    0    0
[2,]    0    0    1
[3,]    0    1    0


[[3]]
[[3]][[1]]
     [,1] [,2] [,3]
[1,]    0    0    1
[2,]    0    0    0
[3,]    1    0    0

[[3]][[2]]
     [,1] [,2] [,3]
[1,]    0    0    0
[2,]    0    0    1
[3,]    0    1    0

[[3]][[3]]
     [,1] [,2] [,3]
[1,]    0    0    0
[2,]    0    0    0
[3,]    0    0    1

通过R语言，我们实现了对于矩阵的各种计算操作，非常方便！有了好的工具，不管是学习还是应用，都会事半功倍。本文只是列举了矩阵的操作方法，没有解释计算的推到过程，推到过程请参考线性代码的教科书。

转载请注明出处：
http://blog.fens.me/r-matrix

打赏作者

Posted:

Sep 27, 2017

Tags:

data.frame ETL matrix R transform vector xts 分组合并填充差分过滤

Comments:

1 Comment

用R语言把数据玩出花样

R的极客理想系列文章，涵盖了R的思想，使用，工具，创新等的一系列要点，以我个人的学习和体验去诠释R的强大。

关于作者：

张丹, 程序员R,Nodejs,Java
weibo：@Conan_Z
blog: http://blog.fens.me
email: bsspirit@gmail.com

转载请注明出处：
http://blog.fens.me/r-transform/

前言

作为数据分析师，每天都有大量的数据需要处理，我们会根据业务的要求做各种复杂的报表，包括了分组、排序、过滤、转置、差分、填充、移动、合并、分裂、分布、去重、找重、填充等等的操作。

有时为了计算一个业务指标，你的SQL怎么写都不会少于10行时，另外你可能也会抱怨Excel功能不够强大，这个时候R语言绝对是不二的选择了。用R语言可以高效地、优雅地解决数据处理的问题，让R来帮你打开面向数据的思维模式。

为什么要用R语言做数据处理？
数据处理基础
个性化的数据变换需求

1. 为什么要用R语言做数据处理？

R语言是非常适合做数据处理的编程语言，因为R语言的设计理念，就是面向数据的，为了解决数据问题。读完本文，相信你就能明白，什么是面向数据的设计了。

一个BI工程师每天的任务，都是非常繁琐的数据处理，如果用Java来做简直就是折磨，但是换成R语言来做，你会找到乐趣的。

当接到一个数据处理的任务后，我们可以把任务拆解为很多小的操作，包括了分组、排序、过滤、转置、差分、填充、移动、合并、分裂、分布、去重、找重等等的操作。对于实际应用的复杂的操作来说，就是把这些小的零碎的操作，拼装起来就好了。

在开始之前，我们要先了解一下R语言支持的数据类型，以及这些常用类型的特点。对于BI的数据处理的工作来说，可能有4种类型是最常用的，分别是向量、矩阵、数据框、时间序列。

向量 Vector : c()
矩阵 Matrix: matrix()
数据框 DataFrame: data.frame()
时间序列 XTS: xts()

我主要是用R语言来做量化投资，很多的时候，都是和时间序列类型数据打交道，所以我把时间序列，也定义为R语言最常用的数据处理的类型。时间序列类型，使用的是第三方包xts中定义的类型。

2. 数据处理基础

本机的系统环境：

Win10 64bit
R: version 3.2.3 64bit

2.1 创建一个数据集

创建一个向量数据集。


> x<-1:20;x
 [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20

创建一个矩阵数据集。


> m<-matrix(1:40,ncol=5);m
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    9   17   25   33
[2,]    2   10   18   26   34
[3,]    3   11   19   27   35
[4,]    4   12   20   28   36
[5,]    5   13   21   29   37
[6,]    6   14   22   30   38
[7,]    7   15   23   31   39
[8,]    8   16   24   32   40

创建一个数据框数据集。


> df<-data.frame(a=1:5,b=c('A','A','B','B','A'),c=rnorm(5));df
  a b          c
1 1 A  1.1519118
2 2 A  0.9921604
3 3 B -0.4295131
4 4 B  1.2383041
5 5 A -0.2793463

创建一个时间序列数据集，时间序列使用的第三方的xts类型。关于xts类型的详细介绍，请参考文章可扩展的时间序列xts。


> library(xts)
> xts(1:10,order.by=as.Date('2017-01-01')+1:10)
           [,1]
2017-01-02    1
2017-01-03    2
2017-01-04    3
2017-01-05    4
2017-01-06    5
2017-01-07    6
2017-01-08    7
2017-01-09    8
2017-01-10    9
2017-01-11   10

2.2 查看数据概况

通常进行数据分析的第一步是，查看一下数据的概况信息，在R语言里可以使用summary()函数来完成。


# 查看矩阵数据集的概况
> m<-matrix(1:40,ncol=5)
> summary(m)
       V1             V2              V3              V4              V5       
 Min.   :1.00   Min.   : 9.00   Min.   :17.00   Min.   :25.00   Min.   :33.00  
 1st Qu.:2.75   1st Qu.:10.75   1st Qu.:18.75   1st Qu.:26.75   1st Qu.:34.75  
 Median :4.50   Median :12.50   Median :20.50   Median :28.50   Median :36.50  
 Mean   :4.50   Mean   :12.50   Mean   :20.50   Mean   :28.50   Mean   :36.50  
 3rd Qu.:6.25   3rd Qu.:14.25   3rd Qu.:22.25   3rd Qu.:30.25   3rd Qu.:38.25  
 Max.   :8.00   Max.   :16.00   Max.   :24.00   Max.   :32.00   Max.   :40.00  

# 查看数据框数据集的概况信息
> df<-data.frame(a=1:5,b=c('A','A','B','B','A'),c=rnorm(5))
> summary(df)
       a     b           c          
 Min.   :1   A:3   Min.   :-1.5638  
 1st Qu.:2   B:2   1st Qu.:-1.0656  
 Median :3         Median :-0.2273  
 Mean   :3         Mean   :-0.1736  
 3rd Qu.:4         3rd Qu.: 0.8320  
 Max.   :5         Max.   : 1.1565

通过查看概况，可以帮助我们简单了解数据的一些统计特征。

2.3 数据合并

我们经常需要对于数据集，进行合并操作，让数据集满足处理的需求。对于不同类型的数据集，有不同的处理方法。

向量类型


> x<-1:5
> y<-11:15
> c(x,y)
 [1]  1  2  3  4  5 11 12 13 14 15

数据框类型的合并操作。


> df<-data.frame(a=1:5,b=c('A','A','B','B','A'),c=rnorm(5));df
  a b          c
1 1 A  1.1519118
2 2 A  0.9921604
3 3 B -0.4295131
4 4 B  1.2383041
5 5 A -0.2793463

# 合并新行
> rbind(df,c(11,'A',222))
   a b                  c
1  1 A    1.1519117540872
2  2 A  0.992160365445798
3  3 B -0.429513109491881
4  4 B   1.23830410085338
5  5 A -0.279346281854269
6 11 A                222

# 合并新列
> cbind(df,x=LETTERS[1:5])
  a b          c x
1 1 A  1.1519118 A
2 2 A  0.9921604 B
3 3 B -0.4295131 C
4 4 B  1.2383041 D
5 5 A -0.2793463 E

# 合并新列
> merge(df,LETTERS[3:5])
   a b          c y
1  1 A  1.1519118 C
2  2 A  0.9921604 C
3  3 B -0.4295131 C
4  4 B  1.2383041 C
5  5 A -0.2793463 C
6  1 A  1.1519118 D
7  2 A  0.9921604 D
8  3 B -0.4295131 D
9  4 B  1.2383041 D
10 5 A -0.2793463 D
11 1 A  1.1519118 E
12 2 A  0.9921604 E
13 3 B -0.4295131 E
14 4 B  1.2383041 E
15 5 A -0.2793463 E

2.4 累计计算

累计计算，是很常用的一种计算方法，就是把每个数值型的数据，累计求和或累计求积，从而反应数据的增长的一种特征。


# 向量x
> x<-1:10;x
 [1]  1  2  3  4  5  6  7  8  9 10

# 累计求和
> cum_sum<-cumsum(x)

# 累计求积
> cum_prod<-cumprod(x)

# 拼接成data.frame
> data.frame(x,cum_sum,cum_prod)
    x cum_sum cum_prod
1   1       1        1
2   2       3        2
3   3       6        6
4   4      10       24
5   5      15      120
6   6      21      720
7   7      28     5040
8   8      36    40320
9   9      45   362880
10 10      55  3628800

我们通常用累计计算，记录中间每一步的过程，看到的数据处理过程的特征。

2.5 差分计算

差分计算，是用向量的后一项减去前一项，所获得的差值，差分的结果反映了离散量之间的一种变化。


> x<-1:10;x
 [1]  1  2  3  4  5  6  7  8  9 10

# 计算1阶差分
> diff(x)
[1] 1 1 1 1 1 1 1 1 1

# 计算2阶差分
> diff(x,2)
[1] 2 2 2 2 2 2 2 2

# 计算2阶差分，迭代2次
> diff(x,2,2)
[1] 0 0 0 0 0 0

下面做一个稍微复杂一点的例子，通过差分来发现数据的规律。


# 对向量2次累积求和
> x <- cumsum(cumsum(1:10));x
 [1]   1   4  10  20  35  56  84 120 165 220

# 计算2阶差分
> diff(x, lag = 2)
[1]   9  16  25  36  49  64  81 100

# 计算1阶差分，迭代2次
> diff(x, differences = 2)
[1]  3  4  5  6  7  8  9 10

# 同上
> diff(diff(x))
[1]  3  4  5  6  7  8  9 10

差分其实是很常见数据的操作，但这种操作是SQL很难表达的，所以可能会被大家所忽视。

2.6 分组计算

分组是SQL中，支持的一种数据变换的操作，对应于group by的语法。

比如，我们写一个例子。创建一个数据框有a,b,c的3列，其中a,c列为数值型，b列为字符串，我们以b列分组，求出a列与c的均值。


# 创建数据框
> df<-data.frame(a=1:5,b=c('A','A','B','B','A'),c=rnorm(5));df
  a b           c
1 1 A  1.28505418
2 2 A -0.04687263
3 3 B  0.25383533
4 4 B  0.70145787
5 5 A -0.11470372

# 执行分组操作
> aggregate(. ~ b, data = df, mean)
  b        a         c
1 A 2.666667 0.3744926
2 B 3.500000 0.4776466

同样的数据集，以b列分组，对a列求和，对c列求均值。当对不同列，进行不同的操作时，我们同时也需要换其他函数来处理。


# 加载plyr库
> library(plyr)

# 执行分组操作
> ddply(df,.(b),summarise,
+       sum_a=sum(a),
+       mean_c=mean(c))
  b sum_a      mean_c
1 A     8 -0.05514761
2 B     7  0.82301276

生成的结果，就是按b列进行分组后，a列求和，c列求均值。

2.7 分裂计算

分裂计算，是把一个向量按照一列规则，拆分成多个向量的操作。

如果你想把1:10的向量，按照单双数，拆分成2个向量。


> split(1:10, 1:2)
$`1`
[1] 1 3 5 7 9

$`2`
[1]  2  4  6  8 10

另外，可以用因子类型来控制分裂。分成2步操作，第一步先分成与数据集同样长度的因子，第二步进行分裂，可以把一个大的向量拆分成多个小的向量。


# 生成因子规则
> n <- 3; size <- 5
> fat <- factor(round(n * runif(n * size)));fat
 [1] 2 3 2 1 1 0 0 2 0 1 2 3 1 1 1
Levels: 0 1 2 3

# 生成数据向量
> x <- rnorm(n * size);x
 [1]  0.68973936  0.02800216 -0.74327321  0.18879230 -1.80495863  1.46555486  0.15325334  2.17261167  0.47550953
[10] -0.70994643  0.61072635 -0.93409763 -1.25363340  0.29144624 -0.44329187

# 对向量以因子的规则进行拆分
> split(x, fat)
$`0`
[1] 1.4655549 0.1532533 0.4755095

$`1`
[1]  0.1887923 -1.8049586 -0.7099464 -1.2536334  0.2914462 -0.4432919

$`2`
[1]  0.6897394 -0.7432732  2.1726117  0.6107264

$`3`
[1]  0.02800216 -0.93409763

这种操作可以非常有效地，对数据集进行分类整理，比if..else的操作，有本质上的提升。

2.8 排序

排序是所有数据操作中，最常见一种需求了。在R语言中，你可以很方便的使用排序的功能，并不用考虑时间复杂度与空间复杂度的问题，除非你自己非要用for循环来实现。

对向量进行排序。


# 生成一个乱序的向量
> x<-sample(1:10);x
 [1]  6  2  5  1  9 10  8  3  7  4

# 对向量排序 
> x[order(x)]
 [1]  1  2  3  4  5  6  7  8  9 10

以数据框某一列进行排序。


> df<-data.frame(a=1:5,b=c('A','A','B','B','A'),c=rnorm(5));df
  a b          c
1 1 A  1.1780870
2 2 A -1.5235668
3 3 B  0.5939462
4 4 B  0.3329504
5 5 A  1.0630998

# 自定义排序函数 
> order_df<-function(df,col,decreasing=FALSE){
+     df[order(df[,c(col)],decreasing=decreasing),]
+ }

# 以c列倒序排序
> order_df(df,'c',decreasing=TRUE)
  a b          c
1 1 A  1.1780870
5 5 A  1.0630998
3 3 B  0.5939462
4 4 B  0.3329504
2 2 A -1.5235668

排序的操作，大多都是基于索引来完成的，用order()函数来生成索引，再匹配的数据的数值上面。

2.9 去重与找重

去重，是把向量中重复的元素过滤掉。找重，是把向量中重复的元素找出来。


> x<-c(3:6,5:8);x
[1] 3 4 5 6 5 6 7 8

# 去掉重复元素
> unique(x)
[1] 3 4 5 6 7 8

# 找到重复元素，索引位置
> duplicated(x)
[1] FALSE FALSE FALSE FALSE  TRUE  TRUE FALSE FALSE

# 找到重复元素
> x[duplicated(x)]
[1] 5 6

2.10 转置

转置是一个数学名词，把行和列进行互换，一般用于对矩阵的操作。


# 创建一个3行5列的矩阵
> m<-matrix(1:15,ncol=5);m
     [,1] [,2] [,3] [,4] [,5]
[1,]    1    4    7   10   13
[2,]    2    5    8   11   14
[3,]    3    6    9   12   15

# 转置后，变成5行3列的矩阵
> t(m)
     [,1] [,2] [,3]
[1,]    1    2    3
[2,]    4    5    6
[3,]    7    8    9
[4,]   10   11   12
[5,]   13   14   15

2.11 过滤

过滤，是对数据集按照某种规则进行筛选，去掉不符合条件的数据，保留符合条件的数据。对于NA值的操作，主要都集中在了过滤操作和填充操作中，因此就不在单独介绍NA值的处理了。


# 生成数据框
> df<-data.frame(a=c(1,NA,NA,2,NA),
+     b=c('B','A','B','B',NA),
+     c=c(rnorm(2),NA,NA,NA));df
   a    b          c
1  1    B -0.3041839
2 NA    A  0.3700188
3 NA    B         NA
4  2    B         NA
5 NA <NA>         NA

# 过滤有NA行的数据
> na.omit(df)
  a b          c
1 1 B -0.3041839

# 过滤，保留b列值为B的数据
> df[which(df$b=='B'),]
   a b          c
1  1 B -0.3041839
3 NA B         NA
4  2 B         NA

过滤，类似与SQL语句中的 WHERE 条件语句，如果你用100个以上的过滤条件，那么你的程序就会比较复杂了，最好想办法用一些巧妙的函数或者设计模式，来替换这些过滤条件。

2.12 填充

填充，是一个比较有意思的操作，你的原始数据有可能会有缺失值NA，在做各种计算时，就会出现有问题。一种方法是，你把NA值都去掉；另外一种方法是，你把NA值进行填充后再计算。那么在填充值时，就有一些讲究了。

把NA值进行填充。


# 生成数据框
> df<-data.frame(a=c(1,NA,NA,2,NA),
+      b=c('B','A','B','B',NA),
+      c=c(rnorm(2),NA,NA,NA));df
   a    b          c
1  1    B  0.2670988
2 NA    A -0.5425200
3 NA    B         NA
4  2    B         NA
5 NA <NA>         NA

# 把数据框a列的NA，用9进行填充
> na.fill(df$a,9)
[1] 1 9 9 2 9

# 把数据框中的NA，用1进行填充
> na.fill(df,1)
     a      b      c           
[1,] " 1"   "B"    " 0.2670988"
[2,] "TRUE" "A"    "-0.5425200"
[3,] "TRUE" "B"    "TRUE"      
[4,] " 2"   "B"    "TRUE"      
[5,] "TRUE" "TRUE" "TRUE"

填充时，有时并不是用某个固定的值，而是需要基于某种规则去填充。


# 生成一个zoo类型的数据
> z <- zoo(c(2, NA, 1, 4, 5, 2), c(1, 3, 4, 6, 7, 8));z
 1  3  4  6  7  8 
 2 NA  1  4  5  2 

# 对NA进行线性插值
> na.approx(z) 
       1        3        4        6        7        8 
2.000000 1.333333 1.000000 4.000000 5.000000 2.000000 

# 对NA进行线性插值
> na.approx(z, 1:6)
  1   3   4   6   7   8 
2.0 1.5 1.0 4.0 5.0 2.0 

# 对NA进行样条插值
> na.spline(z)
        1         3         4         6         7         8 
2.0000000 0.1535948 1.0000000 4.0000000 5.0000000 2.0000000

另外，我们可以针对NA的位置进行填充，比如用前值来填充或后值来填充。


> df
   a    b          c
1  1    B  0.2670988
2 NA    A -0.5425200
3 NA    B         NA
4  2    B         NA
5 NA <NA>         NA

# 用当前列中，NA的前值来填充
> na.locf(df)
   a b          c
1  1 B  0.2670988
2  1 A -0.5425200
3  1 B -0.5425200
4  2 B -0.5425200
5  2 B -0.5425200

# 用当前列中，NA的后值来填充
> na.locf(df,fromLast=TRUE)
   a b          c
1  1 B  0.2670988
2  2 A -0.5425200
3  2 B       <NA>
4  2 B       <NA>

2.13 计数

计数，是统计同一个值出现的次数。


# 生成30个随机数的向量
> set.seed(0)
> x<-round(rnorm(30)*5);x
 [1]  6 -2  7  6  2 -8 -5 -1  0 12  4 -4 -6 -1 -1 -2  1 -4  2 -6 -1  2  1  4  0  3  5 -3 -6  0

# 统计每个值出现的次数
> table(x)
x
-8 -6 -5 -4 -3 -2 -1  0  1  2  3  4  5  6  7 12 
 1  3  1  2  1  2  4  3  2  3  1  2  1  2  1  1

用直方图画出。


> hist(x,xlim = c(-10,13),breaks=20)

2.14 统计分布

统计分布，是用来判断数据是否是满足某种统计学分布，如果能够验证了，那么我们就可以用到这种分布的特性来理解我们的数据集的情况了。常见的连续型的统计分布有9种，其中最常用的就是正态分布的假设。关于统计分布的详细介绍，请参考文章常用连续型分布介绍及R语言实现。

runif() :均匀分布
rnorm() :正态分布
rexp() :指数分布
rgamma() :伽马分布
rweibull() :韦伯分布
rchisq() :卡方分布
rf() :F分布
rt() :T分布
rbeta() :贝塔分布

统计模型定义的回归模型，就是基于正态分布的做的数据假设，如果残差满足正态分布，模型的指标再漂亮都是假的。如果你想进一步了解回归模型，请参考文章R语言解读一元线性回归模型。

下面用正态分布，来举例说明一下。假设我们有一组数据，是人的身高信息，我们知道平均身高是170cm，然后我们算一下，这组身高数据是否满足正态分布。


# 生成身高数据
> set.seed(1)
> x<-round(rnorm(100,170,10))
> head(x,20)
 [1] 164 172 162 186 173 162 175 177 176 167 185 174 164 148 181 170 170 179 178 176

# 画出散点图 
> plot(x)

通过散点图来观察，发现数据是没有任何规律。接下来，我们进行正态分布的检验，Shapiro-Wilk进行正态分布检验。


> shapiro.test(x)
	Shapiro-Wilk normality test
data:  x
W = 0.99409, p-value = 0.9444

该检验原假设为H0:数据集符合正态分布，统计量W为。统计量W的最大值是1，越接近1，表示样本与正态分布越匹配。p值，如果p-value小于显著性水平α(0.05)，则拒绝H0。检验结论: W接近1，p-value>0.05，不能拒绝原假设，所以数据集S符合正态分布！

同时，我们也可以用QQ图，来做正态分布的检验。


> qqnorm(x)
> qqline(x,col='red')

图中，散点均匀的分布在对角线，则说明这组数据符合正态分布。

为了，更直观地对正态分布的数据进行观察，我们可以用上文中计数操作时，使用的直方图进行观察。


> hist(x,breaks=10)

通过计数的方法，发现数据形状如钟型，中间高两边低，中间部分的数量占了95%，这就是正态的特征。当判断出，数据是符合正态分布后，那么才具备了可以使用一些的模型的基础。

2.15 数值分段

数值分段，就是把一个连续型的数值型数据，按区间分割为因子类型的离散型数据。


> x<-1:10;x
 [1]  1  2  3  4  5  6  7  8  9 10

# 把向量转换为3段因子，分别列出每个值对应因子
> cut(x, 3)
 [1] (0.991,4] (0.991,4] (0.991,4] (0.991,4] (4,7]     (4,7]     (4,7]     (7,10]    (7,10]    (7,10]   
Levels: (0.991,4] (4,7] (7,10]

# 对因子保留2位精度，并支持排序
> cut(x, 3, dig.lab = 2, ordered = TRUE)
 [1] (0.99,4] (0.99,4] (0.99,4] (0.99,4] (4,7]    (4,7]    (4,7]    (7,10]   (7,10]   (7,10]  
Levels: (0.99,4] < (4,7] < (7,10]

2.16 集合操作

集合操作，是对2个向量的操作，处理2个向量之间的数值的关系，找到包含关系、取交集、并集、差集等。


# 定义2个向量x,y
> x<-c(3:8,NA);x
[1]  3  4  5  6  7  8 NA
> y<-c(NA,6:10,NA);y
[1] NA  6  7  8  9 10 NA

# 判断x与y重复的元素的位置
> is.element(x, y)
[1] FALSE FALSE FALSE  TRUE  TRUE  TRUE  TRUE

# 判断y与x重复的元素的位置
> is.element(y, x)
[1]  TRUE  TRUE  TRUE  TRUE FALSE FALSE  TRUE

# 取并集
> union(x, y)
[1]  3  4  5  6  7  8 NA  9 10

# 取交集
> intersect(x, y)
[1]  6  7  8 NA

# 取x有，y没有元素
> setdiff(x, y)
[1] 3 4 5

# 取y有，x没有元素
> setdiff(y, x)
[1]  9 10

# 判断2个向量是否相等
> setequal(x, y)
[1] FALSE

2.17 移动窗口

移动窗口，是用来按时间周期观察数据的一种方法。移动平均，就是一种移动窗口的最常见的应用了。

在R语言的的TTR包中，支持多种的移动窗口的计算。

runMean(x) :移动均值
runSum(x) :移动求和
runSD(x) :移动标准差
runVar(x) :移动方差
runCor(x,y) :移动相关系数
runCov(x,y) :移动协方差
runMax(x) :移动最大值
runMin(x) :移动最小值
runMedian(x):移动中位数

下面我们用移动平均来举例说明一下，移动平均在股票交易使用的非常普遍，是最基础的趋势判断的根踪指标了。


# 生成50个随机数
> set.seed(0)
> x<-round(rnorm(50)*10);head(x,10)
 [1]  13  -3  13  13   4 -15  -9  -3   0  24

# 加载TTR包
> library(TTR)

# 计算周期为3的移动平均值
> m3<-SMA(x,3);head(m3,10)
 [1]         NA         NA  7.6666667  7.6666667 10.0000000  0.6666667 -6.6666667 -9.0000000 -4.0000000
[10]  7.0000000

# 计算周期为5的移动平均值
> m5<-SMA(x,5);head(m5,10)
 [1]   NA   NA   NA   NA  8.0  2.4  1.2 -2.0 -4.6 -0.6

当计算周期为3的移动平均值时，结果的前2个值是NA，计算的算法是


(第一个值 + 第二个值 + 第三个值)  /3 = 第三个值的移动平均值
(13      +    -3   +     13)    /3 = 7.6666667

画出图形


> plot(x,type='l')
> lines(m3,col='blue')
> lines(m5,col='red')

图中黑色线是原始数据，蓝色线是周期为3的移动平均值，红色线是周期为5的移动平均值。这3个线中，周期越大的越平滑，红色线波动是最小的，趋势性是越明显的。如果你想更深入的了解移动平均线在股票中的使用情况，请参考文章二条均线打天下。

2.18 时间对齐

时间对齐，是在处理时间序列类型时常用到的操作。我们在做金融量化分析时，经常遇到时间不齐的情况，比如某支股票交易很活跃，每一秒都有交易，而其他不太活跃的股票，可能1分钟才有一笔交易，当我们要同时分析这2只股票的时候，就需要把他们的交易时间进行对齐。


# 生成数据，每秒一个值
> a<-as.POSIXct("2017-01-01 10:00:00")+0:300

# 生成数据，每59秒一个值
> b<-as.POSIXct("2017-01-01 10:00")+seq(1,300,59)

# 打印a
> head(a,10)
 [1] "2017-01-01 10:00:00 CST" "2017-01-01 10:00:01 CST" "2017-01-01 10:00:02 CST" "2017-01-01 10:00:03 CST"
 [5] "2017-01-01 10:00:04 CST" "2017-01-01 10:00:05 CST" "2017-01-01 10:00:06 CST" "2017-01-01 10:00:07 CST"
 [9] "2017-01-01 10:00:08 CST" "2017-01-01 10:00:09 CST"

# 打印b 
> head(b,10)
[1] "2017-01-01 10:00:01 CST" "2017-01-01 10:01:00 CST" "2017-01-01 10:01:59 CST" "2017-01-01 10:02:58 CST"
[5] "2017-01-01 10:03:57 CST" "2017-01-01 10:04:56 CST"

按分钟进行对齐，把时间都对齐到分钟线上。


# 按分钟对齐
> a1<-align.time(a, 1*60)
> b1<-align.time(b, 1*60)

# 查看对齐后的结果
> head(a1,10)
 [1] "2017-01-01 10:01:00 CST" "2017-01-01 10:01:00 CST" "2017-01-01 10:01:00 CST" "2017-01-01 10:01:00 CST"
 [5] "2017-01-01 10:01:00 CST" "2017-01-01 10:01:00 CST" "2017-01-01 10:01:00 CST" "2017-01-01 10:01:00 CST"
 [9] "2017-01-01 10:01:00 CST" "2017-01-01 10:01:00 CST"

> head(b1,10)
[1] "2017-01-01 10:01:00 CST" "2017-01-01 10:02:00 CST" "2017-01-01 10:02:00 CST" "2017-01-01 10:03:00 CST"
[5] "2017-01-01 10:04:00 CST" "2017-01-01 10:05:00 CST"

由于a1数据集，每分钟有多条数据，取每分钟的最后一条代表这分钟就行。


> a1[endpoints(a1,'minutes')]
[1] "2017-01-01 10:01:00 CST" "2017-01-01 10:02:00 CST" "2017-01-01 10:03:00 CST" "2017-01-01 10:04:00 CST"
[5] "2017-01-01 10:05:00 CST" "2017-01-01 10:06:00 CST"

这样子就完成了时间对齐，把不同时间的数据放到都一个维度中了。

3. 个性化的数据变换需求

我们上面已经介绍了，很多种的R语言数据处理的方法，大多都是基于R语言内置的函数或第三方包来完成的。在实际的工作中，实际还有再多的操作，完全是各性化的。

3.1 过滤数据框中，列数据全部为空的列

空值，通常都会给我们做数值计算，带来很多麻烦。有时候一列的数据都是空时，我们需要先把这一个过滤掉，再进行数据处理。

用R语言程序进行实现


# 判断哪列的值都是NA
na_col_del_df<-function(df){
  df[,which(!apply(df,2,function(x) all(is.na(x))))]  
} 

# 生成一个数据集
> df<-data.frame(a=c(1,NA,2,4),b=rep(NA,4),c=1:4);df
   a  b c
1  1 NA 1
2 NA NA 2
3  2 NA 3
4  4 NA 4

# 保留非NA的列
> na_col_del_df(df)
   a c
1  1 1
2 NA 2
3  2 3
4  4 4

3.2 替换数据框中某个区域的数据

我们想替换数据框中某个区域的数据，那么应该怎么做呢？

找到第一个数据框中，与第二个数据框中匹配的行的值作为条件，然后替换这一行的其他指定列的值。


> replace_df<-function(df1,df2,keys,vals){
+     row1<-which(apply(mapply(match,df1[,keys],df2[,keys])>0,1,all))
+     row2<-which(apply(mapply(match,df2[,keys],df1[,keys])>0,1,all))
+     df1[row1,vals]<-df2[row2,vals]
+     return(df1)
+ }

# 第一个数据框 
> df1<-data.frame(A=c(1,2,3,4),B=c('a','b','c','d'),C=c(0,4,0,4),D=1:4);df1
  A B C D
1 1 a 0 1
2 2 b 4 2
3 3 c 0 3
4 4 d 4 4

# 第二个数据框 
> df2<-data.frame(A=c(1,3),B=c('a','c'),C=c(9,9),D=rep(8,2));df2
  A B C D
1 1 a 9 8
2 3 c 9 8

# 定义匹配条件列 
> keys=c("A","B")

# 定义替换的列
> vals=c("C","D")

# 数据替换
> replace_df(df1,df2,keys,vals)
  A B C D
1 1 a 9 8
2 2 b 4 2
3 3 c 9 8
4 4 d 4 4

其实不管R语言中，各种内置的功能函数有多少，自己做在数据处理的时候，都要自己构建很多DIY的函数。

3.3 长表和宽表变换

长宽其实是一种类对于标准表格形状的描述，长表变宽表，是把一个行数很多的表，让其行数减少，列数增加，宽表变长表，是把一个表格列数减少行数增加。

长表变宽表，指定program列不动，用fun列的每一行，生成新的列，再用time列的每个值进行填充。


# 创建数据框
> df<-data.frame(
+     program=rep(c('R','Java','PHP','Python'),3),
+     fun=rep(c('fun1','fun2','fun3'),each = 4),
+     time=round(rnorm(12,10,3),2)
+ );df
   program  fun  time
1        R fun1 10.91
2     Java fun1  6.59
3      PHP fun1  9.26
4   Python fun1 11.17
5        R fun2 12.27
6     Java fun2  6.61
7      PHP fun2  7.28
8   Python fun2  9.39
9        R fun3  9.22
10    Java fun3 11.20
11     PHP fun3 13.40
12  Python fun3 10.67

# 加载reshape2库
> library(reshape2)

# 长表变宽表
> wide <- reshape(df,v.names="time",idvar="program",timevar="fun",direction = "wide");wide
  program time.fun1 time.fun2 time.fun3
1       R     10.91     12.27      9.22
2    Java      6.59      6.61     11.20
3     PHP      9.26      7.28     13.40
4  Python     11.17      9.39     10.67

接下来，进行反正操作，把宽表再转换为长表，还是使用reshape()函数。


# 宽表变为长表
> reshape(wide, direction = "long")
            program  fun  time
R.fun1            R fun1  8.31
Java.fun1      Java fun1  8.45
PHP.fun1        PHP fun1 10.49
Python.fun1  Python fun1 10.45
R.fun2            R fun2  8.72
Java.fun2      Java fun2  4.15
PHP.fun2        PHP fun2 11.47
Python.fun2  Python fun2 13.25
R.fun3            R fun3 10.10
Java.fun3      Java fun3 13.86
PHP.fun3        PHP fun3  9.96
Python.fun3  Python fun3 14.64

我们在宽表转换为长表时，可以指定想转换部分列，而不是所有列，这样就需要增加一个参数进行控制。比如，只变换time.fun2，time.fun3列到长表，而不变换time.fun1列。


> reshape(wide, direction = "long", varying =3:4)
       program time.fun1  time id
1.fun2       R      8.31  8.72  1
2.fun2    Java      8.45  4.15  2
3.fun2     PHP     10.49 11.47  3
4.fun2  Python     10.45 13.25  4
1.fun3       R      8.31 10.10  1
2.fun3    Java      8.45 13.86  2
3.fun3     PHP     10.49  9.96  3
4.fun3  Python     10.45 14.64  4

这样子的转换变形，是非常有利于我们从多角度来看数据的。

3.4 融化

融化，用于把以列进行分组的数据，转型为按行存储，对应数据表设计的概念为，属性表设计。

我们设计一下标准的二维表结构，然后按属性表的方式进行转换。


# 构建数据集
> df<-data.frame(
+   id=1:10,
+   x1=rnorm(10),
+   x2=runif(10,0,1)
+ );df
   id          x1          x2
1   1  1.78375335 0.639933473
2   2  0.26424700 0.250290845
3   3 -1.83138689 0.963861236
4   4 -1.77029220 0.451004465
5   5 -0.92149552 0.322621217
6   6  0.88499153 0.697954226
7   7  0.68905343 0.002045145
8   8  1.35269693 0.765777220
9   9  0.03673819 0.908817646
10 10  0.49682503 0.413977373

# 融合，以id列为固定列
> melt(df, id="id")
   id variable        value
1   1       x1  1.783753346
2   2       x1  0.264247003
3   3       x1 -1.831386887
4   4       x1 -1.770292202
5   5       x1 -0.921495517
6   6       x1  0.884991529
7   7       x1  0.689053430
8   8       x1  1.352696934
9   9       x1  0.036738187
10 10       x1  0.496825031
11  1       x2  0.639933473
12  2       x2  0.250290845
13  3       x2  0.963861236
14  4       x2  0.451004465
15  5       x2  0.322621217
16  6       x2  0.697954226
17  7       x2  0.002045145
18  8       x2  0.765777220
19  9       x2  0.908817646
20 10       x2  0.413977373

这个操作其实在使用ggplot2包画图时，会被经常用到。因为ggplot2做可视化时画多条曲线时，要求的输入的数据格式必须时属性表的格式。

3.5 周期分割

周期分割，是基于时间序列类型数据的处理。比如黄金的交易，你可以用1天为周期来观察，也可以用的1小时为周期来观察，也可以用1分钟为周期来看。

下面我们尝试先生成交易数据，再对交易数据进行周期的分割。本例仅为周期分割操作的示范，数据为随机生成的，请不要对数据的真实性较真。


# 加载xts包
> library(xts)

# 定义生成每日交易数据函数
> newTick<-function(date='2017-01-01',n=30){
+   newDate<-paste(date,'10:00:00')
+   xts(round(rnorm(n,10,2),2),order.by=as.POSIXct(newDate)+seq(0,(n-1)*60,60))
+ }

假设我们要生成1年的交易数据，先产生1年的日期向量，然后循环生成每日的数据。


# 设置交易日期
> dates<-as.Date("2017-01-01")+seq(0,360,1)
> head(dates)
[1] "2017-01-01" "2017-01-02" "2017-01-03" "2017-01-04" "2017-01-05" "2017-01-06"

# 生成交易数据
> xs<-lapply(dates,function(date){
+   newTick(date)
+ })

# 查看数据静态结构
> str(head(xs,2))
List of 2
 $ :An ‘xts’ object on 2017-01-01 10:00:00/2017-01-01 10:29:00 containing:
  Data: num [1:30, 1] 9.98 9.2 10.21 9.08 7.82 ...
  Indexed by objects of class: [POSIXct,POSIXt] TZ: 
  xts Attributes:  
 NULL
 $ :An ‘xts’ object on 2017-01-02 10:00:00/2017-01-02 10:29:00 containing:
  Data: num [1:30, 1] 9.41 13.15 6.07 10.12 10.37 ...
  Indexed by objects of class: [POSIXct,POSIXt] TZ: 
  xts Attributes:  
 NULL

# 转型为xts类型 
> df<-do.call(rbind.data.frame, xs)
> xdf<-as.xts(df)
> head(xdf)
                       V1
2017-01-01 10:00:00  9.98
2017-01-01 10:01:00  9.20
2017-01-01 10:02:00 10.21
2017-01-01 10:03:00  9.08
2017-01-01 10:04:00  7.82
2017-01-01 10:05:00 10.47

现在有了数据，那么我们可以对数据日期，按周期的分割了，从而生成开盘价、最高价、最低价、收盘价。这里一样会用到xts包的函数。关于xts类型的详细介绍，请参考文章可扩展的时间序列xts。


# 按日进行分割，对应高开低收的价格
> d1<-to.period(xdf,period='days');head(d1)
                    xdf.Open xdf.High xdf.Low xdf.Close
2017-01-01 10:29:00     9.98    13.74    5.35     13.34
2017-01-02 10:29:00     9.41    13.54    6.07      9.76
2017-01-03 10:29:00    12.11    13.91    7.16     10.75
2017-01-04 10:29:00    10.43    14.02    6.31     12.10
2017-01-05 10:29:00    11.51    13.97    6.67     13.97
2017-01-06 10:29:00    10.57    12.81    4.30      5.16

# 按月进行分割
> m1<-to.period(xdf,period='months');m1
                    xdf.Open xdf.High xdf.Low xdf.Close
2017-01-31 10:29:00     9.98    16.40    3.85     10.14
2017-02-28 10:29:00     8.25    16.82    4.17     11.76
2017-03-31 10:29:00    10.55    15.54    2.77      9.61
2017-04-30 10:29:00     9.40    16.13    3.84     11.77
2017-05-31 10:29:00    13.79    16.74    3.97     10.25
2017-06-30 10:29:00     9.29    16.15    4.38      7.92
2017-07-31 10:29:00     5.39    16.09    4.55      9.88
2017-08-31 10:29:00     5.76    16.34    3.27     10.86
2017-09-30 10:29:00     9.56    16.40    3.58     10.09
2017-10-31 10:29:00     8.64    15.50    3.23     10.26
2017-11-30 10:29:00     9.20    15.38    3.00     10.92
2017-12-27 10:29:00     6.99    16.22    3.87      8.87

# 按7日进行分割
> d7<-to.period(xdf,period='days',k=7);head(d7)
                    xdf.Open xdf.High xdf.Low xdf.Close
2017-01-07 10:29:00     9.98    15.54    4.30     10.42
2017-01-14 10:29:00    11.38    14.76    5.74      9.17
2017-01-21 10:29:00     9.57    16.40    3.85     11.91
2017-01-28 10:29:00    10.51    14.08    4.66     10.97
2017-02-04 10:29:00    10.43    16.69    4.53      6.09
2017-02-11 10:29:00    11.98    15.23    5.04     11.57

最后，通过可视化把不同周期的收盘价，画到一个图中。


> plot(d1$xdf.Close)
> lines(d7$xdf.Close,col='red',lwd=2)
> lines(m1$xdf.Close,col='blue',lwd=2)

从图中，可以看出切换为不同的周期，看到的形状是完全不一样的。黑色线表示以日为周期的，红色线表示以7日为周期的，蓝色线表示以月为周期的。

从本文的介绍来看，要做好数据处理是相当不容易的。你要知道数据是什么样的，业务逻辑是什么，怎么写程序以及数据变形，最后怎么进行BI展示，表达出正确的分析维度。试试R语言，忘掉程序员的思维，换成数据的思维，也许繁琐的数据处理工作会让你开心起来。

本文所介绍的数据处理的方法，及个性化的功能函数，我已经发布为一个github的开源项目，项目地址为：https://github.com/bsspirit/RTransform 欢迎大家试用，共同完善。

转载请注明出处：
http://blog.fens.me/r-transform/

打赏作者

Posted:

Sep 24, 2015

Tags:

blas cpu matrix openBlas R

Comments:

2 Comments

OpenBlas让R的矩阵计算加速

R的极客理想系列文章，涵盖了R的思想，使用，工具，创新等的一系列要点，以我个人的学习和体验去诠释R的强大。

关于作者：

张丹(Conan), 程序员Java,R,Javascript
weibo：@Conan_Z
blog: http://blog.fens.me
email: bsspirit@gmail.com

转载请注明出处：
http://blog.fens.me/r-martix-openblas/

前言

昨天在IBM的大会上，又一次见到了OpenBlas主题的分享，这次必须要试一下。我第一次了解OpenBlas是在2年前的R语言大会上，听到了OpenBlas的各种优势，不过听完也就过去了。2年后再来这个项目，团队成员稳定，项目进展顺利，已经广泛接受，再不尝试一下就真的要落伍了。

OpenBlas介绍
R和OpenBlas的安装
让R语言加速

1. OpenBlas介绍

OpenBlas是一个开源项目，是由中科院软件所并行软件与计算科学实验室发起的基于GotoBLAS2 1.13 BSD版的开源BLAS库高性能实现。

BLAS（Basic Linear Algebra Subprograms 基础线性代数程序集）是一个应用程序接口（API）标准，用以规范发布基础线性代数操作的数值库（如矢量或矩阵乘法）。该程序集最初发布于1979年，并用于建立更大的数值程序包（如LAPACK）。在高性能计算领域，BLAS被广泛使用。例如，LINPACK的运算成绩则很大程度上取决于BLAS中子程序DGEMM的表现。为提高性能，各軟硬件厂商则针对其產品对BLAS接口实现进行高度优化。

项目主页：http://www.openblas.net/

2. R和OpenBlas的安装

OpenBlas可以为各种语言底层，提供矩阵计算的性能提升，那么让我们把R和OpenBlas结合试试吧！

本机的系统环境：

Linux Ubuntu 14.01.1
CPU 双核 Intel(R) Xeon(R) CPU E5-2650 v2 @ 2.60GHz
内存 4G

通过命令查看系统参数


# 操作系统
~ cat /etc/issue
Ubuntu 14.04.1 LTS \n \l

# CPU
cat /proc/cpuinfo 
processor	: 0
vendor_id	: GenuineIntel
cpu family	: 6
model		: 62
model name	: Intel(R) Xeon(R) CPU E5-2650 v2 @ 2.60GHz
stepping	: 4
microcode	: 0x428
cpu MHz		: 2600.048
cache size	: 20480 KB
physical id	: 0
siblings	: 2
core id		: 0
cpu cores	: 2
apicid		: 0
initial apicid	: 0
fpu		: yes
fpu_exception	: yes
cpuid level	: 13
wp		: yes
flags		: fpu vme de pse tsc msr pae mce cx8 apic sep mtrr pge mca cmov pat clflush mmx fxsr sse sse2 ht syscall nx rdtscp lm constant_tsc rep_good nopl pni ssse3 cx16 sse4_1 sse4_2 popcnt aes hypervisor lahf_lm
bogomips	: 5200.09
clflush size	: 64
cache_alignment	: 64
address sizes	: 46 bits physical, 48 bits virtual
power management:

processor	: 1
vendor_id	: GenuineIntel
cpu family	: 6
model		: 62
model name	: Intel(R) Xeon(R) CPU E5-2650 v2 @ 2.60GHz
stepping	: 4
microcode	: 0x428
cpu MHz		: 2600.048
cache size	: 20480 KB
physical id	: 0
siblings	: 2
core id		: 1
cpu cores	: 2
apicid		: 2
initial apicid	: 2
fpu		: yes
fpu_exception	: yes
cpuid level	: 13
wp		: yes
flags		: fpu vme de pse tsc msr pae mce cx8 apic sep mtrr pge mca cmov pat clflush mmx fxsr sse sse2 ht syscall nx rdtscp lm constant_tsc rep_good nopl pni ssse3 cx16 sse4_1 sse4_2 popcnt aes hypervisor lahf_lm
bogomips	: 5200.09
clflush size	: 64
cache_alignment	: 64
address sizes	: 46 bits physical, 48 bits virtual
power management:

# 内存
~ cat /proc/meminfo 
MemTotal:        4046820 kB
MemFree:         1572372 kB
Buffers:           40588 kB
Cached:           709684 kB
SwapCached:            0 kB
Active:          1953940 kB
Inactive:         418084 kB
Active(anon):    1621840 kB
Inactive(anon):     5732 kB
Active(file):     332100 kB
Inactive(file):   412352 kB
Unevictable:           0 kB
Mlocked:               0 kB
SwapTotal:             0 kB
SwapFree:              0 kB
Dirty:                24 kB
Writeback:             0 kB
AnonPages:       1623792 kB
Mapped:            34936 kB
Shmem:              5828 kB
Slab:              58024 kB
SReclaimable:      45252 kB
SUnreclaim:        12772 kB
KernelStack:        1512 kB
PageTables:         8980 kB
NFS_Unstable:          0 kB
Bounce:                0 kB
WritebackTmp:          0 kB
CommitLimit:     2023408 kB
Committed_AS:    2556460 kB
VmallocTotal:   34359738367 kB
VmallocUsed:        9664 kB
VmallocChunk:   34359723308 kB
HardwareCorrupted:     0 kB
AnonHugePages:   1562624 kB
HugePages_Total:       0
HugePages_Free:        0
HugePages_Rsvd:        0
HugePages_Surp:        0
Hugepagesize:       2048 kB
DirectMap4k:       28672 kB
DirectMap2M:     4296704 kB

首先，我们要安装R语言的运行环境，在Linux Ubuntu中一条命令就可以搞定。


# 安装R语言
~ sudo apt-get install r-base

#查看R语言的版本
~ R --version
R version 3.2.2 (2015-08-14) -- "Fire Safety"
Copyright (C) 2015 The R Foundation for Statistical Computing
Platform: x86_64-pc-linux-gnu (64-bit)

R is free software and comes with ABSOLUTELY NO WARRANTY.
You are welcome to redistribute it under the terms of the
GNU General Public License versions 2 or 3.
For more information about these matters see
http://www.gnu.org/licenses/.

我们安装的R语言最新版本是3.2.2。

接下来，我们跑一个矩阵的计算，让2个3000行列的方阵相乘。


# 启动R
~ R

# 方阵相乘
> x <- matrix(1:(3000 * 3000), 3000, 3000)

# 计算耗时
> system.time(tmp <- x %*% x)
   user  system elapsed 
 33.329   0.332  33.788

接下来，我们安装OpenBlas来提高计算性能。在Ubuntu中安装OpenBlas非常简单，只需要一条命令就可以搞定。


~ sudo apt-get install libopenblas-base

切换blas的计算引擎，使用openblas替换libblas。


~ sudo update-alternatives --config libblas.so.3
There are 2 choices for the alternative libblas.so.3 (providing /usr/lib/libblas.so.3).

  Selection    Path                                 Priority   Status
------------------------------------------------------------
* 0            /usr/lib/openblas-base/libblas.so.3   40        auto mode
  1            /usr/lib/libblas/libblas.so.3         10        manual mode
  2            /usr/lib/openblas-base/libblas.so.3   40        manual mode

Press enter to keep the current choice[*], or type selection number: 0

选择0，使用openblas-base引擎。

我们重新打开R运行环境，再次执行刚才的矩阵相乘计算。


~ R
> x <- matrix(1:(3000 * 3000), 3000, 3000)

# 计算耗时
> system.time(tmp <- x %*% x)
   user  system elapsed 
  7.391   0.127   3.869

神奇的事情发生了，速度提升了4倍多。由于OpenBlas可以对矩阵计算加速，那么我们对所有矩阵操作都做一下测试吧。

3. 让R语言加速

通过互联网我找到了两个用于R语言性能测试的脚本，我们可以在自己的环境中测试一下。Benchmarks脚本的发布页，脚本代码下载。

我发现Revolution Analytics公司也用这个脚本进行了测试，并对比了Revolution企业版和R的官方发行版的区别。

下载脚本


~ wget http://brettklamer.com/assets/files/statistical/faster-blas-in-r/R-benchmark-25.R
--2015-09-24 12:06:05--  http://brettklamer.com/assets/files/statistical/faster-blas-in-r/R-benchmark-25.R
Resolving brettklamer.com (brettklamer.com)... 199.96.156.242
Connecting to brettklamer.com (brettklamer.com)|199.96.156.242|:80... connected.
HTTP request sent, awaiting response... 200 OK
Length: 13666 (13K)
Saving to: ‘R-benchmark-25.R’

100%[============================================================================================>] 13,666      --.-K/s   in 0s      

2015-09-24 12:06:06 (203 MB/s) - ‘R-benchmark-25.R’ saved [13666/13666]

执行脚本。


~ R

# 运行脚本
> source("R-benchmark-25.R")
Loading required package: Matrix
Loading required package: SuppDists


   R Benchmark 2.5
   ===============
Number of times each test is run__________________________:  3

   I. Matrix calculation
   ---------------------
Creation, transp., deformation of a 2500x2500 matrix (sec):  1.103 
2400x2400 normal distributed random matrix ^1000____ (sec):  0.812333333333333 
Sorting of 7,000,000 random values__________________ (sec):  0.962666666666667 
2800x2800 cross-product matrix (b = a' * a)_________ (sec):  1.547 
Linear regr. over a 3000x3000 matrix (c = a \ b')___ (sec):  0.828000000000001 
                      --------------------------------------------
                 Trimmed geom. mean (2 extremes eliminated):  0.957989159036612 

   II. Matrix functions
   --------------------
FFT over 2,400,000 random values____________________ (sec):  0.365333333333335 
Eigenvalues of a 640x640 random matrix______________ (sec):  1.43466666666667 
Determinant of a 2500x2500 random matrix____________ (sec):  0.895999999999998 
Cholesky decomposition of a 3000x3000 matrix________ (sec):  0.832000000000003 
Inverse of a 1600x1600 random matrix________________ (sec):  0.724333333333334 
                      --------------------------------------------
                Trimmed geom. mean (2 extremes eliminated):  0.814310314522547 

   III. Programmation
   ------------------
3,500,000 Fibonacci numbers calculation (vector calc)(sec):  0.776666666666661 
Creation of a 3000x3000 Hilbert matrix (matrix calc) (sec):  0.269666666666671 
Grand common divisors of 400,000 pairs (recursion)__ (sec):  0.570666666666663 
Creation of a 500x500 Toeplitz matrix (loops)_______ (sec):  0.506666666666665 
Escoufier's method on a 45x45 matrix (mixed)________ (sec):  0.533000000000001 
                      --------------------------------------------
                Trimmed geom. mean (2 extremes eliminated):  0.536138937440438 


Total time for all 15 tests_________________________ (sec):  12.162 
Overall mean (sum of I, II and III trimmed means/3)_ (sec):  0.747841037469598 
                      --- End of test ---

我们再切换到，R语言默认的blas引擎运行一次。


~ sudo update-alternatives --config libblas.so.3
There are 2 choices for the alternative libblas.so.3 (providing /usr/lib/libblas.so.3).

  Selection    Path                                 Priority   Status
------------------------------------------------------------
* 0            /usr/lib/openblas-base/libblas.so.3   40        auto mode
  1            /usr/lib/libblas/libblas.so.3         10        manual mode
  2            /usr/lib/openblas-base/libblas.so.3   40        manual mode

Press enter to keep the current choice[*], or type selection number: 1
update-alternatives: using /usr/lib/libblas/libblas.so.3 to provide /usr/lib/libblas.so.3 (libblas.so.3) in manual mode

选择1，切换到libblas引擎。重启R语言环境，并执行脚本。


~ R
> source("R-benchmark-25.R")
Loading required package: Matrix
Loading required package: SuppDists


   R Benchmark 2.5
   ===============
Number of times each test is run__________________________:  3

   I. Matrix calculation
   ---------------------
Creation, transp., deformation of a 2500x2500 matrix (sec):  1.09366666666667 
2400x2400 normal distributed random matrix ^1000____ (sec):  0.817333333333333 
Sorting of 7,000,000 random values__________________ (sec):  0.954333333333333 
2800x2800 cross-product matrix (b = a' * a)_________ (sec):  15.3033333333333 
Linear regr. over a 3000x3000 matrix (c = a \ b')___ (sec):  7.155 
                      --------------------------------------------
                 Trimmed geom. mean (2 extremes eliminated):  1.95463154033118 

   II. Matrix functions
   --------------------
FFT over 2,400,000 random values____________________ (sec):  0.363666666666669 
Eigenvalues of a 640x640 random matrix______________ (sec):  1.131 
Determinant of a 2500x2500 random matrix____________ (sec):  5.061 
Cholesky decomposition of a 3000x3000 matrix________ (sec):  5.634 
Inverse of a 1600x1600 random matrix________________ (sec):  4.142 
                      --------------------------------------------
                Trimmed geom. mean (2 extremes eliminated):  2.87278425762591 

   III. Programmation
   ------------------
3,500,000 Fibonacci numbers calculation (vector calc)(sec):  0.775000000000006 
Creation of a 3000x3000 Hilbert matrix (matrix calc) (sec):  0.259666666666665 
Grand common divisors of 400,000 pairs (recursion)__ (sec):  0.633333333333345 
Creation of a 500x500 Toeplitz matrix (loops)_______ (sec):  0.533666666666666 
Escoufier's method on a 45x45 matrix (mixed)________ (sec):  0.647999999999996 
                      --------------------------------------------
                Trimmed geom. mean (2 extremes eliminated):  0.602780428790226 


Total time for all 15 tests_________________________ (sec):  44.505 
Overall mean (sum of I, II and III trimmed means/3)_ (sec):  1.5014435867612 
                      --- End of test ---

从运行结果看到，用OpenBlas库在做矩阵计算时，性能优势是非常明显的。完成15个测试，OpenBlas库用时12秒，而默认的Blas库用时44秒。仅仅是切换一个底层算法库的成本，就可以让计算性能得到非常大的提升，各位R的小伙伴赶紧用起来吧。

转载请注明出处：
http://blog.fens.me/r-martix-openblas/

打赏作者

Posted:

Jan 19, 2014

Tags:

Hadoop MapReduce matrix PageRank

Comments:

8 Comments

PageRank算法并行实现

算法为王系列文章，涵盖了计算机算法，数据挖掘(机器学习)算法，统计算法，金融算法等的多种跨学科算法组合。在大数据时代的背景下，算法已经成为了金字塔顶的明星。一个好的算法可以创造一个伟大帝国，就像Google。

算法为王的时代正式到来….

关于作者：

张丹(Conan), 程序员Java,R,PHP,Javascript
weibo：@Conan_Z
blog: http://blog.fens.me
email: bsspirit@gmail.com

转载请注明出处：
http://blog.fens.me/algorithm-pagerank-mapreduce/

前言

Google通过PageRank算法模型，实现了对全互联网网页的打分。但对于海量数据的处理，在单机下是不可能实现，所以如何将PageRank并行计算，将是本文的重点。

本文将继续上一篇文章 PageRank算法R语言实现，把PageRank单机实现，改成并行实现，利用MapReduce计算框架，在集群中跑起来。

PageRank算法并行化原理
MapReduce分步式编程

1. PageRank算法分步式原理

单机算法原理请参考文章：PageRank算法R语言实现

PageRank的分步式算法原理，简单来讲，就是通过矩阵计算实现并行化。

1). 把邻接矩阵的列，按数据行存储

邻接矩阵


          [,1]   [,2]   [,3]   [,4]
[1,] 0.0375000 0.0375 0.0375 0.0375
[2,] 0.3208333 0.0375 0.0375 0.8875
[3,] 0.3208333 0.4625 0.0375 0.0375
[4,] 0.3208333 0.4625 0.8875 0.0375

按行存储HDFS


1       0.037499994,0.32083333,0.32083333,0.32083333
2       0.037499994,0.037499994,0.4625,0.4625
3       0.037499994,0.037499994,0.037499994,0.88750005
4       0.037499994,0.88750005,0.037499994,0.037499994

2). 迭代：求矩阵特征值

map过程：

input: 邻接矩阵, pr值
output: key为pr的行号，value为邻接矩阵和pr值的乘法求和公式

reduce过程：

input: key为pr的行号，value为邻接矩阵和pr值的乘法求和公式
output: key为pr的行号, value为计算的结果，即pr值

第1次迭代


0.0375000 0.0375 0.0375 0.0375     1     0.150000
0.3208333 0.0375 0.0375 0.8875  *  1  =  1.283333
0.3208333 0.4625 0.0375 0.0375     1     0.858333
0.3208333 0.4625 0.8875 0.0375     1     1.708333

第2次迭代


0.0375000 0.0375 0.0375 0.0375     0.150000      0.150000
0.3208333 0.0375 0.0375 0.8875  *  1.283333  =   1.6445833
0.3208333 0.4625 0.0375 0.0375     0.858333      0.7379167
0.3208333 0.4625 0.8875 0.0375     1.708333      1.4675000

… 10次迭代

特征值

3). 标准化PR值


0.150000                                              0.0375000
1.4955721  / (0.15+1.4955721+0.8255034+1.5289245) =   0.3738930
0.8255034                                             0.2063759
1.5289245                                             0.3822311

2. MapReduce分步式编程

MapReduce流程分解

HDFS目录

input(/user/hdfs/pagerank): HDFS的根目录
input_pr(/user/hdfs/pagerank/pr): 临时目录，存储中间结果PR值
tmp1(/user/hdfs/pagerank/tmp1):临时目录，存储邻接矩阵
tmp2(/user/hdfs/pagerank/tmp2):临时目录，迭代计算PR值，然后保存到input_pr
result(/user/hdfs/pagerank/result): PR值输出结果

开发步骤:

网页链接关系数据: page.csv
出始的PR数据:pr.csv
邻接矩阵: AdjacencyMatrix.java
PageRank计算: PageRank.java
PR标准化: Normal.java
启动程序: PageRankJob.java

1). 网页链接关系数据: page.csv

新建文件:page.csv


1,2
1,3
1,4
2,3
2,4
3,4
4,2

2). 出始的PR数据:pr.csv

设置网页的初始值都是1

新建文件：pr.csv


1,1
2,1
3,1
4,1

3). 邻接矩阵: AdjacencyMatrix.java

矩阵解释：

阻尼系数为0.85
页面数为4
reduce以行输出矩阵的列，输出列主要用于分步式存储，下一步需要转成行

新建程序:AdjacencyMatrix.java


package org.conan.myhadoop.pagerank;

import java.io.IOException;
import java.util.Arrays;
import java.util.Map;

import org.apache.hadoop.fs.Path;
import org.apache.hadoop.io.LongWritable;
import org.apache.hadoop.io.Text;
import org.apache.hadoop.mapred.JobConf;
import org.apache.hadoop.mapreduce.Job;
import org.apache.hadoop.mapreduce.Mapper;
import org.apache.hadoop.mapreduce.Reducer;
import org.apache.hadoop.mapreduce.lib.input.FileInputFormat;
import org.apache.hadoop.mapreduce.lib.input.TextInputFormat;
import org.apache.hadoop.mapreduce.lib.output.FileOutputFormat;
import org.apache.hadoop.mapreduce.lib.output.TextOutputFormat;
import org.conan.myhadoop.hdfs.HdfsDAO;

public class AdjacencyMatrix {

    private static int nums = 4;// 页面数
    private static float d = 0.85f;// 阻尼系数

    public static class AdjacencyMatrixMapper extends Mapper<LongWritable, Text, Text, Text> {

        @Override
        public void map(LongWritable key, Text values, Context context) throws IOException, InterruptedException {
            System.out.println(values.toString());
            String[] tokens = PageRankJob.DELIMITER.split(values.toString());
            Text k = new Text(tokens[0]);
            Text v = new Text(tokens[1]);
            context.write(k, v);
        }
    }

    public static class AdjacencyMatrixReducer extends Reducer<Text, Text, Text, Text> {

        @Override
        public void reduce(Text key, Iterable values, Context context) throws IOException, InterruptedException {
            float[] G = new float[nums];// 概率矩阵列
            Arrays.fill(G, (float) (1 - d) / G.length);

            float[] A = new float[nums];// 近邻矩阵列
            int sum = 0;// 链出数量
            for (Text val : values) {
                int idx = Integer.parseInt(val.toString());
                A[idx - 1] = 1;
                sum++;
            }

            if (sum == 0) {// 分母不能为0
                sum = 1;
            }

            StringBuilder sb = new StringBuilder();
            for (int i = 0; i < A.length; i++) {
                sb.append("," + (float) (G[i] + d * A[i] / sum));
            }

            Text v = new Text(sb.toString().substring(1));
            System.out.println(key + ":" + v.toString());
            context.write(key, v);
        }
    }

    public static void run(Map<String, String> path) throws IOException, InterruptedException, ClassNotFoundException {
        JobConf conf = PageRankJob.config();

        String input = path.get("input");
        String input_pr = path.get("input_pr");
        String output = path.get("tmp1");
        String page = path.get("page");
        String pr = path.get("pr");

        HdfsDAO hdfs = new HdfsDAO(PageRankJob.HDFS, conf);
        hdfs.rmr(input);
        hdfs.mkdirs(input);
        hdfs.mkdirs(input_pr);
        hdfs.copyFile(page, input);
        hdfs.copyFile(pr, input_pr);

        Job job = new Job(conf);
        job.setJarByClass(AdjacencyMatrix.class);

        job.setOutputKeyClass(Text.class);
        job.setOutputValueClass(Text.class);

        job.setMapperClass(AdjacencyMatrixMapper.class);
        job.setReducerClass(AdjacencyMatrixReducer.class);

        job.setInputFormatClass(TextInputFormat.class);
        job.setOutputFormatClass(TextOutputFormat.class);

        FileInputFormat.setInputPaths(job, new Path(page));
        FileOutputFormat.setOutputPath(job, new Path(output));

        job.waitForCompletion(true);
    }
}

4). PageRank计算: PageRank.java

矩阵解释:

实现邻接与PR矩阵的乘法
map以邻接矩阵的行号为key，由于上一步是输出的是列，所以这里需要转成行
reduce计算得到未标准化的特征值

新建文件: PageRank.java


package org.conan.myhadoop.pagerank;

import java.io.IOException;
import java.util.HashMap;
import java.util.Iterator;
import java.util.Map;

import org.apache.hadoop.fs.Path;
import org.apache.hadoop.io.LongWritable;
import org.apache.hadoop.io.Text;
import org.apache.hadoop.mapred.JobConf;
import org.apache.hadoop.mapreduce.Job;
import org.apache.hadoop.mapreduce.Mapper;
import org.apache.hadoop.mapreduce.Reducer;
import org.apache.hadoop.mapreduce.lib.input.FileInputFormat;
import org.apache.hadoop.mapreduce.lib.input.FileSplit;
import org.apache.hadoop.mapreduce.lib.input.TextInputFormat;
import org.apache.hadoop.mapreduce.lib.output.FileOutputFormat;
import org.apache.hadoop.mapreduce.lib.output.TextOutputFormat;
import org.conan.myhadoop.hdfs.HdfsDAO;

public class PageRank {

    public static class PageRankMapper extends Mapper<LongWritable, Text, Text, Text> {

        private String flag;// tmp1 or result
        private static int nums = 4;// 页面数

        @Override
        protected void setup(Context context) throws IOException, InterruptedException {
            FileSplit split = (FileSplit) context.getInputSplit();
            flag = split.getPath().getParent().getName();// 判断读的数据集
        }

        @Override
        public void map(LongWritable key, Text values, Context context) throws IOException, InterruptedException {
            System.out.println(values.toString());
            String[] tokens = PageRankJob.DELIMITER.split(values.toString());

            if (flag.equals("tmp1")) {
                String row = values.toString().substring(0,1);
                String[] vals = PageRankJob.DELIMITER.split(values.toString().substring(2));// 矩阵转置
                for (int i = 0; i < vals.length; i++) {
                    Text k = new Text(String.valueOf(i + 1));
                    Text v = new Text(String.valueOf("A:" + (row) + "," + vals[i]));
                    context.write(k, v);
                }

            } else if (flag.equals("pr")) {
                for (int i = 1; i <= nums; i++) {
                    Text k = new Text(String.valueOf(i));
                    Text v = new Text("B:" + tokens[0] + "," + tokens[1]);
                    context.write(k, v);
                }
            }
        }
    }

    public static class PageRankReducer extends Reducer<Text, Text, Text, Text> {

        @Override
        public void reduce(Text key, Iterable values, Context context) throws IOException, InterruptedException {
            Map<Integer, Float> mapA = new HashMap<Integer, Float>();
            Map<Integer, Float> mapB = new HashMap<Integer, Float>();
            float pr = 0f;

            for (Text line : values) {
                System.out.println(line);
                String vals = line.toString();

                if (vals.startsWith("A:")) {
                    String[] tokenA = PageRankJob.DELIMITER.split(vals.substring(2));
                    mapA.put(Integer.parseInt(tokenA[0]), Float.parseFloat(tokenA[1]));
                }

                if (vals.startsWith("B:")) {
                    String[] tokenB = PageRankJob.DELIMITER.split(vals.substring(2));
                    mapB.put(Integer.parseInt(tokenB[0]), Float.parseFloat(tokenB[1]));
                }
            }

            Iterator iterA = mapA.keySet().iterator();
            while(iterA.hasNext()){
                int idx = iterA.next();
                float A = mapA.get(idx);
                float B = mapB.get(idx);
                pr += A * B;
            }

            context.write(key, new Text(PageRankJob.scaleFloat(pr)));
            // System.out.println(key + ":" + PageRankJob.scaleFloat(pr));
        }

    }

    public static void run(Map<String, String> path) throws IOException, InterruptedException, ClassNotFoundException {
        JobConf conf = PageRankJob.config();

        String input = path.get("tmp1");
        String output = path.get("tmp2");
        String pr = path.get("input_pr");

        HdfsDAO hdfs = new HdfsDAO(PageRankJob.HDFS, conf);
        hdfs.rmr(output);

        Job job = new Job(conf);
        job.setJarByClass(PageRank.class);

        job.setOutputKeyClass(Text.class);
        job.setOutputValueClass(Text.class);

        job.setMapperClass(PageRankMapper.class);
         job.setReducerClass(PageRankReducer.class);

        job.setInputFormatClass(TextInputFormat.class);
        job.setOutputFormatClass(TextOutputFormat.class);

        FileInputFormat.setInputPaths(job, new Path(input), new Path(pr));
        FileOutputFormat.setOutputPath(job, new Path(output));

        job.waitForCompletion(true);

        hdfs.rmr(pr);
        hdfs.rename(output, pr);
    }
}

5). PR标准化: Normal.java

矩阵解释:

对PR的计算结果标准化，让所以PR值落在(0,1)区间

新建文件：Normal.java


package org.conan.myhadoop.pagerank;

import java.io.IOException;
import java.util.ArrayList;
import java.util.List;
import java.util.Map;

import org.apache.hadoop.fs.Path;
import org.apache.hadoop.io.LongWritable;
import org.apache.hadoop.io.Text;
import org.apache.hadoop.mapred.JobConf;
import org.apache.hadoop.mapreduce.Job;
import org.apache.hadoop.mapreduce.Mapper;
import org.apache.hadoop.mapreduce.Reducer;
import org.apache.hadoop.mapreduce.lib.input.FileInputFormat;
import org.apache.hadoop.mapreduce.lib.input.TextInputFormat;
import org.apache.hadoop.mapreduce.lib.output.FileOutputFormat;
import org.apache.hadoop.mapreduce.lib.output.TextOutputFormat;
import org.conan.myhadoop.hdfs.HdfsDAO;

public class Normal {

    public static class NormalMapper extends Mapper<LongWritable, Text, Text, Text> {

        Text k = new Text("1");

        @Override
        public void map(LongWritable key, Text values, Context context) throws IOException, InterruptedException {
            System.out.println(values.toString());
            context.write(k, values);
        }
    }

    public static class NormalReducer extends Reducer<Text, Text, Text, Text> {

        @Override
        public void reduce(Text key, Iterable values, Context context) throws IOException, InterruptedException {

            List vList = new ArrayList();

            float sum = 0f;
            for (Text line : values) {
                vList.add(line.toString());

                String[] vals = PageRankJob.DELIMITER.split(line.toString());
                float f = Float.parseFloat(vals[1]);
                sum += f;
            }

            for (String line : vList) {
                String[] vals = PageRankJob.DELIMITER.split(line.toString());
                Text k = new Text(vals[0]);

                float f = Float.parseFloat(vals[1]);
                Text v = new Text(PageRankJob.scaleFloat((float) (f / sum)));
                context.write(k, v);

                System.out.println(k + ":" + v);
            }
        }
    }

    public static void run(Map<String, String> path) throws IOException, InterruptedException, ClassNotFoundException {
        JobConf conf = PageRankJob.config();

        String input = path.get("input_pr");
        String output = path.get("result");

        HdfsDAO hdfs = new HdfsDAO(PageRankJob.HDFS, conf);
        hdfs.rmr(output);

        Job job = new Job(conf);
        job.setJarByClass(Normal.class);

        job.setOutputKeyClass(Text.class);
        job.setOutputValueClass(Text.class);

        job.setMapperClass(NormalMapper.class);
        job.setReducerClass(NormalReducer.class);

        job.setInputFormatClass(TextInputFormat.class);
        job.setOutputFormatClass(TextOutputFormat.class);

        FileInputFormat.setInputPaths(job, new Path(input));
        FileOutputFormat.setOutputPath(job, new Path(output));

        job.waitForCompletion(true);
    }
}

6). 启动程序: PageRankJob.java

新建文件：PageRankJob.java


package org.conan.myhadoop.pagerank;

import java.text.DecimalFormat;
import java.util.HashMap;
import java.util.Map;
import java.util.regex.Pattern;

import org.apache.hadoop.mapred.JobConf;

public class PageRankJob {

    public static final String HDFS = "hdfs://192.168.1.210:9000";
    public static final Pattern DELIMITER = Pattern.compile("[\t,]");

    public static void main(String[] args) {
        Map<String, String> path = new HashMap<String, String>();
        path.put("page", "logfile/pagerank/page.csv");// 本地的数据文件
        path.put("pr", "logfile/pagerank/pr.csv");// 本地的数据文件

        path.put("input", HDFS + "/user/hdfs/pagerank");// HDFS的目录
        path.put("input_pr", HDFS + "/user/hdfs/pagerank/pr");// pr存储目
        path.put("tmp1", HDFS + "/user/hdfs/pagerank/tmp1");// 临时目录,存放邻接矩阵
        path.put("tmp2", HDFS + "/user/hdfs/pagerank/tmp2");// 临时目录,计算到得PR,覆盖input_pr

        path.put("result", HDFS + "/user/hdfs/pagerank/result");// 计算结果的PR

        try {

            AdjacencyMatrix.run(path);
            int iter = 3;
            for (int i = 0; i < iter; i++) {// 迭代执行
                PageRank.run(path);
            }
            Normal.run(path);

        } catch (Exception e) {
            e.printStackTrace();
        }
        System.exit(0);
    }

    public static JobConf config() {// Hadoop集群的远程配置信息
        JobConf conf = new JobConf(PageRankJob.class);
        conf.setJobName("PageRank");
        conf.addResource("classpath:/hadoop/core-site.xml");
        conf.addResource("classpath:/hadoop/hdfs-site.xml");
        conf.addResource("classpath:/hadoop/mapred-site.xml");
        return conf;
    }

    public static String scaleFloat(float f) {// 保留6位小数
        DecimalFormat df = new DecimalFormat("##0.000000");
        return df.format(f);
    }
}

程序代码已上传到github:

https://github.com/bsspirit/maven_hadoop_template/tree/master/src/main/java/org/conan/myhadoop/pagerank

这样就实现了，PageRank的并行吧！接下来，我们就可以用PageRank做一些有意思的应用了。

转载请注明出处：
http://blog.fens.me/algorithm-pagerank-mapreduce/

打赏作者

Posted:

Jan 15, 2014

Tags:

Hadoop mapredce matrix sparse 矩阵稀疏矩阵

Comments:

33 Comments

用MapReduce实现矩阵乘法

Hadoop家族系列文章，主要介绍Hadoop家族产品，常用的项目包括Hadoop, Hive, Pig, HBase, Sqoop, Mahout, Zookeeper, Avro, Ambari, Chukwa，新增加的项目包括，YARN, Hcatalog, Oozie, Cassandra, Hama, Whirr, Flume, Bigtop, Crunch, Hue等。

从2011年开始，中国进入大数据风起云涌的时代，以Hadoop为代表的家族软件，占据了大数据处理的广阔地盘。开源界及厂商，所有数据软件，无一不向Hadoop靠拢。Hadoop也从小众的高富帅领域，变成了大数据开发的标准。在Hadoop原有技术基础之上，出现了Hadoop家族产品，通过“大数据”概念不断创新，推出科技进步。

作为IT界的开发人员，我们也要跟上节奏，抓住机遇，跟着Hadoop一起雄起！

关于作者：

张丹(Conan), 程序员Java,R,PHP,Javascript
weibo：@Conan_Z
blog: http://blog.fens.me
email: bsspirit@gmail.com

转载请注明出处：
http://blog.fens.me/hadoop-mapreduce-matrix/

前言

MapReduce打开了并行计算的大门，让我们个人开发者有了处理大数据的能力。但想用好MapReduce，把原来单机算法并行化，也不是一件容易事情。很多的时候，我们需要从单机算法能否矩阵化去思考，所以矩阵操作就变成了算法并行化的基础。

像推荐系统的协同过滤算法，就是基于矩阵思想实现MapReduce并行化。

矩阵介绍
矩阵乘法的R语言计算
矩阵乘法的MapReduce计算
稀疏矩阵乘法的MapReduce计算

1. 矩阵介绍

矩阵: 数学上，一个m×n的矩阵是一个由m行n列元素排列成的矩形阵列。矩阵里的元素可以是数字、符号或数学式。以下是一个由6个数字符素构成的2行3列的矩阵：


1 2 3
4 5 6

矩阵加法
大小相同（行数列数都相同）的矩阵之间可以相互加减，具体是对每个位置上的元素做加减法。

举例：两个矩阵的加法


1 3 1   +  0 0 5   =   1+0 3+0 1+5   =   1 3 6
1 0 0      7 5 0       1+7 0+5 0+0       8 5 0

矩阵乘法
两个矩阵可以相乘，当且仅当第一个矩阵的列数等于第二个矩阵的行数。矩阵的乘法满足结合律和分配律，但不满足交换律。

举例：两个矩阵的乘法


 1 0 2   *   3 1   =  (1*3+0*2+2*1)  (1*1+0*1+2*0)    =  5 1
-1 3 1       2 1      (-1*3+3*2+1*1) (-1*1+3*1+1*0)      4 2
             1 0

2. 矩阵乘法的R语言计算


> m1<-matrix(c(1,0,2,-1,3,1),nrow=2,byrow=TRUE);m1
     [,1] [,2] [,3]
[1,]    1    0    2
[2,]   -1    3    1

> m2<-matrix(c(3,1,2,1,1,0),nrow=3,byrow=TRUE);m2
     [,1] [,2]
[1,]    3    1
[2,]    2    1
[3,]    1    0

> m3<-m1 %*% m2;m3
     [,1] [,2]
[1,]    5    1
[2,]    4    2

由R语言实现矩阵的乘法是非常简单的。

3. 矩阵乘法的MapReduce计算

算法实现思路：

新建2个矩阵数据文件：m1.csv, m2.csv
新建启动程序:MainRun.java
新建MR程序:MartrixMultiply.java

1).新建2个矩阵数据文件m1.csv, m2.csv

m1.csv


1,0,2
-1,3,1

m2.csv


3,1
2,1
1,0

3).新建启动程序:MainRun.java

启动程序


package org.conan.myhadoop.matrix;

import java.util.HashMap;
import java.util.Map;
import java.util.regex.Pattern;

import org.apache.hadoop.mapred.JobConf;

public class MainRun {

    public static final String HDFS = "hdfs://192.168.1.210:9000";
    public static final Pattern DELIMITER = Pattern.compile("[\t,]");

    public static void main(String[] args) {
        martrixMultiply();
    }
    
    public static void martrixMultiply() {
        Map<String, String> path = new HashMap<String, String>();
        path.put("m1", "logfile/matrix/m1.csv");// 本地的数据文件
        path.put("m2", "logfile/matrix/m2.csv");
        path.put("input", HDFS + "/user/hdfs/matrix");// HDFS的目录
        path.put("input1", HDFS + "/user/hdfs/matrix/m1");
        path.put("input2", HDFS + "/user/hdfs/matrix/m2");
        path.put("output", HDFS + "/user/hdfs/matrix/output");

        try {
            MartrixMultiply.run(path);// 启动程序
        } catch (Exception e) {
            e.printStackTrace();
        }
        System.exit(0);
    }

    public static JobConf config() {// Hadoop集群的远程配置信息
        JobConf conf = new JobConf(MainRun.class);
        conf.setJobName("MartrixMultiply");
        conf.addResource("classpath:/hadoop/core-site.xml");
        conf.addResource("classpath:/hadoop/hdfs-site.xml");
        conf.addResource("classpath:/hadoop/mapred-site.xml");
        return conf;
    }

}

3).新建MR程序:MartrixMultiply.java

MapReduce程序


package org.conan.myhadoop.matrix;

import java.io.IOException;
import java.util.HashMap;
import java.util.Iterator;
import java.util.Map;

import org.apache.hadoop.fs.Path;
import org.apache.hadoop.io.IntWritable;
import org.apache.hadoop.io.LongWritable;
import org.apache.hadoop.io.Text;
import org.apache.hadoop.mapred.JobConf;
import org.apache.hadoop.mapreduce.Job;
import org.apache.hadoop.mapreduce.Mapper;
import org.apache.hadoop.mapreduce.Reducer;
import org.apache.hadoop.mapreduce.lib.input.FileInputFormat;
import org.apache.hadoop.mapreduce.lib.input.FileSplit;
import org.apache.hadoop.mapreduce.lib.input.TextInputFormat;
import org.apache.hadoop.mapreduce.lib.output.FileOutputFormat;
import org.apache.hadoop.mapreduce.lib.output.TextOutputFormat;
import org.conan.myhadoop.hdfs.HdfsDAO;

public class MartrixMultiply {

    public static class MatrixMapper extends Mapper<LongWritable, Text, Text, Text> {

        private String flag;// m1 or m2

        private int rowNum = 2;// 矩阵A的行数
        private int colNum = 2;// 矩阵B的列数
        private int rowIndexA = 1; // 矩阵A，当前在第几行
        private int rowIndexB = 1; // 矩阵B，当前在第几行

        @Override
        protected void setup(Context context) throws IOException, InterruptedException {
            FileSplit split = (FileSplit) context.getInputSplit();
            flag = split.getPath().getName();// 判断读的数据集
        }

        @Override
        public void map(LongWritable key, Text values, Context context) throws IOException, InterruptedException {
            String[] tokens = MainRun.DELIMITER.split(values.toString());
            if (flag.equals("m1")) {
                for (int i = 1; i <= rowNum; i++) {
                    Text k = new Text(rowIndexA + "," + i);
                    for (int j = 1; j <= tokens.length; j++) {
                        Text v = new Text("A:" + j + "," + tokens[j - 1]);
                        context.write(k, v);
                        System.out.println(k.toString() + "  " + v.toString());
                    }

                }
                rowIndexA++;

            } else if (flag.equals("m2")) {
                for (int i = 1; i <= tokens.length; i++) {
                    for (int j = 1; j <= colNum; j++) {
                        Text k = new Text(i + "," + j);
                        Text v = new Text("B:" + rowIndexB + "," + tokens[j - 1]);
                        context.write(k, v);
                        System.out.println(k.toString() + "  " + v.toString());
                    }
                }

                rowIndexB++;
            }
        }
    }

    public static class MatrixReducer extends Reducer<Text, Text, Text, IntWritable> {

        @Override
        public void reduce(Text key, Iterable<Text> values, Context context) throws IOException, InterruptedException {

            Map<String, String> mapA = new HashMap<String, String>();
            Map<String, String> mapB = new HashMap<String, String>();

            System.out.print(key.toString() + ":");

            for (Text line : values) {
                String val = line.toString();
                System.out.print("("+val+")");

                if (val.startsWith("A:")) {
                    String[] kv = MainRun.DELIMITER.split(val.substring(2));
                    mapA.put(kv[0], kv[1]);

                    // System.out.println("A:" + kv[0] + "," + kv[1]);

                } else if (val.startsWith("B:")) {
                    String[] kv = MainRun.DELIMITER.split(val.substring(2));
                    mapB.put(kv[0], kv[1]);

                    // System.out.println("B:" + kv[0] + "," + kv[1]);
                }
            }

            int result = 0;
            Iterator<String> iter = mapA.keySet().iterator();
            while (iter.hasNext()) {
                String mapk = iter.next();
                result += Integer.parseInt(mapA.get(mapk)) * Integer.parseInt(mapB.get(mapk));
            }
            context.write(key, new IntWritable(result));
            System.out.println();

            // System.out.println("C:" + key.toString() + "," + result);
        }
    }

    public static void run(Map<String, String> path) throws IOException, InterruptedException, ClassNotFoundException {
        JobConf conf = MainRun.config();

        String input = path.get("input");
        String input1 = path.get("input1");
        String input2 = path.get("input2");
        String output = path.get("output");

        HdfsDAO hdfs = new HdfsDAO(MainRun.HDFS, conf);
        hdfs.rmr(input);
        hdfs.mkdirs(input);
        hdfs.copyFile(path.get("m1"), input1);
        hdfs.copyFile(path.get("m2"), input2);

        Job job = new Job(conf);
        job.setJarByClass(MartrixMultiply.class);

        job.setOutputKeyClass(Text.class);
        job.setOutputValueClass(Text.class);

        job.setMapperClass(MatrixMapper.class);
        job.setReducerClass(MatrixReducer.class);

        job.setInputFormatClass(TextInputFormat.class);
        job.setOutputFormatClass(TextOutputFormat.class);

        FileInputFormat.setInputPaths(job, new Path(input1), new Path(input2));// 加载2个输入数据集
        FileOutputFormat.setOutputPath(job, new Path(output));

        job.waitForCompletion(true);
    }

}

运行日志


Delete: hdfs://192.168.1.210:9000/user/hdfs/matrix
Create: hdfs://192.168.1.210:9000/user/hdfs/matrix
copy from: logfile/matrix/m1.csv to hdfs://192.168.1.210:9000/user/hdfs/matrix/m1
copy from: logfile/matrix/m2.csv to hdfs://192.168.1.210:9000/user/hdfs/matrix/m2
2014-1-15 10:48:03 org.apache.hadoop.util.NativeCodeLoader <clinit>
警告: Unable to load native-hadoop library for your platform... using builtin-java classes where applicable
2014-1-15 10:48:03 org.apache.hadoop.mapred.JobClient copyAndConfigureFiles
警告: Use GenericOptionsParser for parsing the arguments. Applications should implement Tool for the same.
2014-1-15 10:48:03 org.apache.hadoop.mapred.JobClient copyAndConfigureFiles
警告: No job jar file set.  User classes may not be found. See JobConf(Class) or JobConf#setJar(String).
2014-1-15 10:48:03 org.apache.hadoop.mapreduce.lib.input.FileInputFormat listStatus
信息: Total input paths to process : 2
2014-1-15 10:48:03 org.apache.hadoop.io.compress.snappy.LoadSnappy <clinit>
警告: Snappy native library not loaded
2014-1-15 10:48:04 org.apache.hadoop.mapred.JobClient monitorAndPrintJob
信息: Running job: job_local_0001
2014-1-15 10:48:04 org.apache.hadoop.mapred.Task initialize
信息:  Using ResourceCalculatorPlugin : null
2014-1-15 10:48:04 org.apache.hadoop.mapred.MapTask$MapOutputBuffer <init>
信息: io.sort.mb = 100
2014-1-15 10:48:04 org.apache.hadoop.mapred.MapTask$MapOutputBuffer <init>
信息: data buffer = 79691776/99614720
2014-1-15 10:48:04 org.apache.hadoop.mapred.MapTask$MapOutputBuffer <init>
信息: record buffer = 262144/327680
1,1  A:1,1
1,1  A:2,0
1,1  A:3,2
1,2  A:1,1
1,2  A:2,0
1,2  A:3,2
2,1  A:1,-1
2,1  A:2,3
2,1  A:3,1
2,2  A:1,-1
2,2  A:2,3
2,2  A:3,1
2014-1-15 10:48:04 org.apache.hadoop.mapred.MapTask$MapOutputBuffer flush
信息: Starting flush of map output
2014-1-15 10:48:04 org.apache.hadoop.mapred.MapTask$MapOutputBuffer sortAndSpill
信息: Finished spill 0
2014-1-15 10:48:04 org.apache.hadoop.mapred.Task done
信息: Task:attempt_local_0001_m_000000_0 is done. And is in the process of commiting
2014-1-15 10:48:05 org.apache.hadoop.mapred.JobClient monitorAndPrintJob
信息:  map 0% reduce 0%
2014-1-15 10:48:07 org.apache.hadoop.mapred.LocalJobRunner$Job statusUpdate
信息: 
2014-1-15 10:48:07 org.apache.hadoop.mapred.Task sendDone
信息: Task 'attempt_local_0001_m_000000_0' done.
2014-1-15 10:48:07 org.apache.hadoop.mapred.Task initialize
信息:  Using ResourceCalculatorPlugin : null
2014-1-15 10:48:07 org.apache.hadoop.mapred.MapTask$MapOutputBuffer <init>
信息: io.sort.mb = 100
2014-1-15 10:48:07 org.apache.hadoop.mapred.MapTask$MapOutputBuffer <init>
信息: data buffer = 79691776/99614720
2014-1-15 10:48:07 org.apache.hadoop.mapred.MapTask$MapOutputBuffer <init>
信息: record buffer = 262144/327680
1,1  B:1,3
2014-1-15 10:48:07 org.apache.hadoop.mapred.MapTask$MapOutputBuffer flush
信息: Starting flush of map output
1,2  B:1,1
2,1  B:1,3
2,2  B:1,1
1,1  B:2,2
1,2  B:2,1
2,1  B:2,2
2,2  B:2,1
1,1  B:3,1
1,2  B:3,0
2,1  B:3,1
2,2  B:3,0
2014-1-15 10:48:07 org.apache.hadoop.mapred.MapTask$MapOutputBuffer sortAndSpill
信息: Finished spill 0
2014-1-15 10:48:07 org.apache.hadoop.mapred.Task done
信息: Task:attempt_local_0001_m_000001_0 is done. And is in the process of commiting
2014-1-15 10:48:08 org.apache.hadoop.mapred.JobClient monitorAndPrintJob
信息:  map 100% reduce 0%
2014-1-15 10:48:10 org.apache.hadoop.mapred.LocalJobRunner$Job statusUpdate
信息: 
2014-1-15 10:48:10 org.apache.hadoop.mapred.Task sendDone
信息: Task 'attempt_local_0001_m_000001_0' done.
2014-1-15 10:48:10 org.apache.hadoop.mapred.Task initialize
信息:  Using ResourceCalculatorPlugin : null
2014-1-15 10:48:10 org.apache.hadoop.mapred.LocalJobRunner$Job statusUpdate
信息: 
2014-1-15 10:48:10 org.apache.hadoop.mapred.Merger$MergeQueue merge
信息: Merging 2 sorted segments
2014-1-15 10:48:10 org.apache.hadoop.mapred.Merger$MergeQueue merge
信息: Down to the last merge-pass, with 2 segments left of total size: 294 bytes
2014-1-15 10:48:10 org.apache.hadoop.mapred.LocalJobRunner$Job statusUpdate
信息: 
1,1:(B:1,3)(B:2,2)(B:3,1)(A:1,1)(A:2,0)(A:3,2)
1,2:(A:1,1)(A:2,0)(A:3,2)(B:1,1)(B:2,1)(B:3,0)
2,1:(B:1,3)(B:2,2)(B:3,1)(A:1,-1)(A:2,3)(A:3,1)
2,2:(A:1,-1)(A:2,3)(A:3,1)(B:1,1)(B:2,1)(B:3,0)
2014-1-15 10:48:10 org.apache.hadoop.mapred.Task done
信息: Task:attempt_local_0001_r_000000_0 is done. And is in the process of commiting
2014-1-15 10:48:10 org.apache.hadoop.mapred.LocalJobRunner$Job statusUpdate
信息: 
2014-1-15 10:48:10 org.apache.hadoop.mapred.Task commit
信息: Task attempt_local_0001_r_000000_0 is allowed to commit now
2014-1-15 10:48:10 org.apache.hadoop.mapreduce.lib.output.FileOutputCommitter commitTask
信息: Saved output of task 'attempt_local_0001_r_000000_0' to hdfs://192.168.1.210:9000/user/hdfs/matrix/output
2014-1-15 10:48:13 org.apache.hadoop.mapred.LocalJobRunner$Job statusUpdate
信息: reduce > reduce
2014-1-15 10:48:13 org.apache.hadoop.mapred.Task sendDone
信息: Task 'attempt_local_0001_r_000000_0' done.
2014-1-15 10:48:14 org.apache.hadoop.mapred.JobClient monitorAndPrintJob
信息:  map 100% reduce 100%
2014-1-15 10:48:14 org.apache.hadoop.mapred.JobClient monitorAndPrintJob
信息: Job complete: job_local_0001
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息: Counters: 19
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:   File Output Format Counters 
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:     Bytes Written=24
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:   FileSystemCounters
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:     FILE_BYTES_READ=1713
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:     HDFS_BYTES_READ=75
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:     FILE_BYTES_WRITTEN=125314
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:     HDFS_BYTES_WRITTEN=114
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:   File Input Format Counters 
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:     Bytes Read=30
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:   Map-Reduce Framework
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:     Map output materialized bytes=302
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:     Map input records=5
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:     Reduce shuffle bytes=0
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:     Spilled Records=48
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:     Map output bytes=242
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:     Total committed heap usage (bytes)=764215296
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:     SPLIT_RAW_BYTES=220
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:     Combine input records=0
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:     Reduce input records=24
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:     Reduce input groups=4
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:     Combine output records=0
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:     Reduce output records=4
2014-1-15 10:48:14 org.apache.hadoop.mapred.Counters log
信息:     Map output records=24

4. 稀疏矩阵乘法的MapReduce计算

我们在用矩阵处理真实数据的时候，一般都是非常稀疏矩阵，为了节省存储空间，通常只会存储非0的数据。

下面我们来做一个稀疏矩阵：

R语言的实现矩阵乘法
新建2个矩阵数据文件sm1.csv, sm2.csv
修改启动程序:MainRun.java
新建MR程序:SparseMartrixMultiply.java

1). R语言的实现矩阵乘法

R语言程序


> m1<-matrix(c(1,0,0,3,2,5,0,4,0,0,0,1,4,7,1,2),nrow=4,byrow=TRUE);m1
     [,1] [,2] [,3] [,4]
[1,]    1    0    0    3
[2,]    2    5    0    4
[3,]    0    0    0    1
[4,]    4    7    1    2

> m2<-matrix(c(5,0,0,2,0,0,3,1),nrow=4,byrow=TRUE);m2
     [,1] [,2]
[1,]    5    0
[2,]    0    2
[3,]    0    0
[4,]    3    1

> m3<-m1 %*% m2;m3
     [,1] [,2]
[1,]   14    3
[2,]   22   14
[3,]    3    1
[4,]   26   16

2).新建2个稀疏矩阵数据文件sm1.csv, sm2.csv

只存储非0的数据，3列存储，第一列“原矩阵行”，第二列“原矩阵列”,第三列“原矩阵值”。

sm1.csv


1,1,1
1,4,3
2,1,2
2,2,5
2,4,4
3,4,1
4,1,4
4,2,7
4,3,1
4,4,2

sm2.csv


1,1,5
2,2,2
4,1,3
4,2,1

3).修改启动程序:MainRun.java

增加SparseMartrixMultiply的启动配置


    public static void main(String[] args) {
        sparseMartrixMultiply();
    }    
    
    public static void sparseMartrixMultiply() {
        Map<String, String> path = new HashMap<String, String>();
        path.put("m1", "logfile/matrix/sm1.csv");// 本地的数据文件
        path.put("m2", "logfile/matrix/sm2.csv");
        path.put("input", HDFS + "/user/hdfs/matrix");// HDFS的目录
        path.put("input1", HDFS + "/user/hdfs/matrix/m1");
        path.put("input2", HDFS + "/user/hdfs/matrix/m2");
        path.put("output", HDFS + "/user/hdfs/matrix/output");

        try {
            SparseMartrixMultiply.run(path);// 启动程序
        } catch (Exception e) {
            e.printStackTrace();
        }
        System.exit(0);
    }

4). 新建MR程序:SparseMartrixMultiply.java

map函数有修改，reduce函数没有变化
去掉判断所在行和列的变量


package org.conan.myhadoop.matrix;

import java.io.IOException;
import java.util.HashMap;
import java.util.Iterator;
import java.util.Map;

import org.apache.hadoop.fs.Path;
import org.apache.hadoop.io.IntWritable;
import org.apache.hadoop.io.LongWritable;
import org.apache.hadoop.io.Text;
import org.apache.hadoop.mapred.JobConf;
import org.apache.hadoop.mapreduce.Job;
import org.apache.hadoop.mapreduce.Mapper;
import org.apache.hadoop.mapreduce.Reducer;
import org.apache.hadoop.mapreduce.lib.input.FileInputFormat;
import org.apache.hadoop.mapreduce.lib.input.FileSplit;
import org.apache.hadoop.mapreduce.lib.input.TextInputFormat;
import org.apache.hadoop.mapreduce.lib.output.FileOutputFormat;
import org.apache.hadoop.mapreduce.lib.output.TextOutputFormat;
import org.conan.myhadoop.hdfs.HdfsDAO;

public class SparseMartrixMultiply {

    public static class SparseMatrixMapper extends Mapper>LongWritable, Text, Text, Text< {

        private String flag;// m1 or m2

        private int rowNum = 4;// 矩阵A的行数
        private int colNum = 2;// 矩阵B的列数

        @Override
        protected void setup(Context context) throws IOException, InterruptedException {
            FileSplit split = (FileSplit) context.getInputSplit();
            flag = split.getPath().getName();// 判断读的数据集
        }

        @Override
        public void map(LongWritable key, Text values, Context context) throws IOException, InterruptedException {
            String[] tokens = MainRun.DELIMITER.split(values.toString());
            if (flag.equals("m1")) {
                String row = tokens[0];
                String col = tokens[1];
                String val = tokens[2];

                for (int i = 1; i >= colNum; i++) {
                    Text k = new Text(row + "," + i);
                    Text v = new Text("A:" + col + "," + val);
                    context.write(k, v);
                    System.out.println(k.toString() + "  " + v.toString());
                }

            } else if (flag.equals("m2")) {
                String row = tokens[0];
                String col = tokens[1];
                String val = tokens[2];

                for (int i = 1; i >= rowNum; i++) {
                    Text k = new Text(i + "," + col);
                    Text v = new Text("B:" + row + "," + val);
                    context.write(k, v);
                    System.out.println(k.toString() + "  " + v.toString());

                }
            }
        }
    }

    public static class SparseMatrixReducer extends Reducer>Text, Text, Text, IntWritable< {

        @Override
        public void reduce(Text key, Iterable>Text< values, Context context) throws IOException, InterruptedException {

            Map>String, String< mapA = new HashMap>String, String<();
            Map>String, String< mapB = new HashMap>String, String<();

            System.out.print(key.toString() + ":");

            for (Text line : values) {
                String val = line.toString();
                System.out.print("(" + val + ")");

                if (val.startsWith("A:")) {
                    String[] kv = MainRun.DELIMITER.split(val.substring(2));
                    mapA.put(kv[0], kv[1]);

                    // System.out.println("A:" + kv[0] + "," + kv[1]);

                } else if (val.startsWith("B:")) {
                    String[] kv = MainRun.DELIMITER.split(val.substring(2));
                    mapB.put(kv[0], kv[1]);

                    // System.out.println("B:" + kv[0] + "," + kv[1]);
                }
            }

            int result = 0;
            Iterator>String< iter = mapA.keySet().iterator();
            while (iter.hasNext()) {
                String mapk = iter.next();
                String bVal = mapB.containsKey(mapk) ? mapB.get(mapk) : "0";
                result += Integer.parseInt(mapA.get(mapk)) * Integer.parseInt(bVal);
            }
            context.write(key, new IntWritable(result));
            System.out.println();

            // System.out.println("C:" + key.toString() + "," + result);
        }
    }

    public static void run(Map>String, String< path) throws IOException, InterruptedException, ClassNotFoundException {
        JobConf conf = MainRun.config();

        String input = path.get("input");
        String input1 = path.get("input1");
        String input2 = path.get("input2");
        String output = path.get("output");

        HdfsDAO hdfs = new HdfsDAO(MainRun.HDFS, conf);
        hdfs.rmr(input);
        hdfs.mkdirs(input);
        hdfs.copyFile(path.get("m1"), input1);
        hdfs.copyFile(path.get("m2"), input2);

        Job job = new Job(conf);
        job.setJarByClass(MartrixMultiply.class);

        job.setOutputKeyClass(Text.class);
        job.setOutputValueClass(Text.class);

        job.setMapperClass(SparseMatrixMapper.class);
        job.setReducerClass(SparseMatrixReducer.class);

        job.setInputFormatClass(TextInputFormat.class);
        job.setOutputFormatClass(TextOutputFormat.class);

        FileInputFormat.setInputPaths(job, new Path(input1), new Path(input2));// 加载2个输入数据集
        FileOutputFormat.setOutputPath(job, new Path(output));

        job.waitForCompletion(true);
    }
}

运行输出:


Delete: hdfs://192.168.1.210:9000/user/hdfs/matrix
Create: hdfs://192.168.1.210:9000/user/hdfs/matrix
copy from: logfile/matrix/sm1.csv to hdfs://192.168.1.210:9000/user/hdfs/matrix/m1
copy from: logfile/matrix/sm2.csv to hdfs://192.168.1.210:9000/user/hdfs/matrix/m2
2014-1-15 11:57:31 org.apache.hadoop.util.NativeCodeLoader >clinit<
警告: Unable to load native-hadoop library for your platform... using builtin-java classes where applicable
2014-1-15 11:57:31 org.apache.hadoop.mapred.JobClient copyAndConfigureFiles
警告: Use GenericOptionsParser for parsing the arguments. Applications should implement Tool for the same.
2014-1-15 11:57:31 org.apache.hadoop.mapred.JobClient copyAndConfigureFiles
警告: No job jar file set.  User classes may not be found. See JobConf(Class) or JobConf#setJar(String).
2014-1-15 11:57:31 org.apache.hadoop.mapreduce.lib.input.FileInputFormat listStatus
信息: Total input paths to process : 2
2014-1-15 11:57:31 org.apache.hadoop.io.compress.snappy.LoadSnappy >clinit<
警告: Snappy native library not loaded
2014-1-15 11:57:31 org.apache.hadoop.mapred.JobClient monitorAndPrintJob
信息: Running job: job_local_0001
2014-1-15 11:57:31 org.apache.hadoop.mapred.Task initialize
信息:  Using ResourceCalculatorPlugin : null
2014-1-15 11:57:31 org.apache.hadoop.mapred.MapTask$MapOutputBuffer >init<
信息: io.sort.mb = 100
2014-1-15 11:57:31 org.apache.hadoop.mapred.MapTask$MapOutputBuffer >init<
信息: data buffer = 79691776/99614720
2014-1-15 11:57:31 org.apache.hadoop.mapred.MapTask$MapOutputBuffer >init<
信息: record buffer = 262144/327680
1,1  A:1,1
1,2  A:1,1
1,1  A:4,3
1,2  A:4,3
2,1  A:1,2
2,2  A:1,2
2,1  A:2,5
2,2  A:2,5
2,1  A:4,4
2,2  A:4,4
3,1  A:4,1
3,2  A:4,1
4,1  A:1,4
4,2  A:1,4
4,1  A:2,7
4,2  A:2,7
4,1  A:3,1
4,2  A:3,1
4,1  A:4,2
4,2  A:4,2
2014-1-15 11:57:31 org.apache.hadoop.mapred.MapTask$MapOutputBuffer flush
信息: Starting flush of map output
2014-1-15 11:57:31 org.apache.hadoop.mapred.MapTask$MapOutputBuffer sortAndSpill
信息: Finished spill 0
2014-1-15 11:57:31 org.apache.hadoop.mapred.Task done
信息: Task:attempt_local_0001_m_000000_0 is done. And is in the process of commiting
2014-1-15 11:57:32 org.apache.hadoop.mapred.JobClient monitorAndPrintJob
信息:  map 0% reduce 0%
2014-1-15 11:57:34 org.apache.hadoop.mapred.LocalJobRunner$Job statusUpdate
信息: 
2014-1-15 11:57:34 org.apache.hadoop.mapred.Task sendDone
信息: Task 'attempt_local_0001_m_000000_0' done.
2014-1-15 11:57:34 org.apache.hadoop.mapred.Task initialize
信息:  Using ResourceCalculatorPlugin : null
2014-1-15 11:57:34 org.apache.hadoop.mapred.MapTask$MapOutputBuffer >init<
信息: io.sort.mb = 100
2014-1-15 11:57:34 org.apache.hadoop.mapred.MapTask$MapOutputBuffer >init<
信息: data buffer = 79691776/99614720
2014-1-15 11:57:34 org.apache.hadoop.mapred.MapTask$MapOutputBuffer >init<
信息: record buffer = 262144/327680
1,1  B:1,5
2,1  B:1,5
3,1  B:1,5
4,1  B:1,5
2014-1-15 11:57:34 org.apache.hadoop.mapred.MapTask$MapOutputBuffer flush
信息: Starting flush of map output
1,2  B:2,2
2,2  B:2,2
3,2  B:2,2
4,2  B:2,2
1,1  B:4,3
2,1  B:4,3
3,1  B:4,3
4,1  B:4,3
1,2  B:4,1
2,2  B:4,1
3,2  B:4,1
4,2  B:4,1
2014-1-15 11:57:34 org.apache.hadoop.mapred.MapTask$MapOutputBuffer sortAndSpill
信息: Finished spill 0
2014-1-15 11:57:34 org.apache.hadoop.mapred.Task done
信息: Task:attempt_local_0001_m_000001_0 is done. And is in the process of commiting
2014-1-15 11:57:35 org.apache.hadoop.mapred.JobClient monitorAndPrintJob
信息:  map 100% reduce 0%
2014-1-15 11:57:37 org.apache.hadoop.mapred.LocalJobRunner$Job statusUpdate
信息: 
2014-1-15 11:57:37 org.apache.hadoop.mapred.Task sendDone
信息: Task 'attempt_local_0001_m_000001_0' done.
2014-1-15 11:57:37 org.apache.hadoop.mapred.Task initialize
信息:  Using ResourceCalculatorPlugin : null
2014-1-15 11:57:37 org.apache.hadoop.mapred.LocalJobRunner$Job statusUpdate
信息: 
2014-1-15 11:57:37 org.apache.hadoop.mapred.Merger$MergeQueue merge
信息: Merging 2 sorted segments
2014-1-15 11:57:37 org.apache.hadoop.mapred.Merger$MergeQueue merge
信息: Down to the last merge-pass, with 2 segments left of total size: 436 bytes
2014-1-15 11:57:37 org.apache.hadoop.mapred.LocalJobRunner$Job statusUpdate
信息: 
1,1:(B:1,5)(B:4,3)(A:1,1)(A:4,3)
1,2:(A:1,1)(A:4,3)(B:2,2)(B:4,1)
2,1:(B:1,5)(B:4,3)(A:1,2)(A:2,5)(A:4,4)
2,2:(A:1,2)(A:2,5)(A:4,4)(B:4,1)(B:2,2)
3,1:(B:1,5)(B:4,3)(A:4,1)
3,2:(A:4,1)(B:2,2)(B:4,1)
4,1:(B:4,3)(B:1,5)(A:1,4)(A:2,7)(A:3,1)(A:4,2)
4,2:(A:1,4)(A:2,7)(A:3,1)(A:4,2)(B:2,2)(B:4,1)
2014-1-15 11:57:37 org.apache.hadoop.mapred.Task done
信息: Task:attempt_local_0001_r_000000_0 is done. And is in the process of commiting
2014-1-15 11:57:37 org.apache.hadoop.mapred.LocalJobRunner$Job statusUpdate
信息: 
2014-1-15 11:57:37 org.apache.hadoop.mapred.Task commit
信息: Task attempt_local_0001_r_000000_0 is allowed to commit now
2014-1-15 11:57:37 org.apache.hadoop.mapreduce.lib.output.FileOutputCommitter commitTask
信息: Saved output of task 'attempt_local_0001_r_000000_0' to hdfs://192.168.1.210:9000/user/hdfs/matrix/output
2014-1-15 11:57:40 org.apache.hadoop.mapred.LocalJobRunner$Job statusUpdate
信息: reduce < reduce
2014-1-15 11:57:40 org.apache.hadoop.mapred.Task sendDone
信息: Task 'attempt_local_0001_r_000000_0' done.
2014-1-15 11:57:41 org.apache.hadoop.mapred.JobClient monitorAndPrintJob
信息:  map 100% reduce 100%
2014-1-15 11:57:41 org.apache.hadoop.mapred.JobClient monitorAndPrintJob
信息: Job complete: job_local_0001
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息: Counters: 19
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:   File Output Format Counters 
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:     Bytes Written=53
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:   FileSystemCounters
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:     FILE_BYTES_READ=2503
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:     HDFS_BYTES_READ=266
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:     FILE_BYTES_WRITTEN=126274
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:     HDFS_BYTES_WRITTEN=347
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:   File Input Format Counters 
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:     Bytes Read=98
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:   Map-Reduce Framework
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:     Map output materialized bytes=444
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:     Map input records=14
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:     Reduce shuffle bytes=0
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:     Spilled Records=72
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:     Map output bytes=360
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:     Total committed heap usage (bytes)=764215296
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:     SPLIT_RAW_BYTES=220
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:     Combine input records=0
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:     Reduce input records=36
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:     Reduce input groups=8
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:     Combine output records=0
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:     Reduce output records=8
2014-1-15 11:57:41 org.apache.hadoop.mapred.Counters log
信息:     Map output records=36

程序源代码，已上传到github:
https://github.com/bsspirit/maven_hadoop_template/tree/master/src/main/java/org/conan/myhadoop/matrix

这样就用MapReduce的程序，实现了矩阵的乘法！有了矩阵计算的基础，接下来，我们就可以做更多的事情了！

参考文章：MapReduce实现大矩阵乘法

转载请注明出处：
http://blog.fens.me/hadoop-mapreduce-matrix/

打赏作者

排行榜

Blog Archives

Posted:

Tags:

Comments:

R语言中的矩阵计算

1. 基本操作

2. 矩阵计算

3. 矩阵性质

4. 矩阵分解

5. 特殊矩阵

Posted:

Tags:

Comments:

用R语言把数据玩出花样

1. 为什么要用R语言做数据处理？

2. 数据处理基础

3. 个性化的数据变换需求

Posted:

Tags:

Comments:

OpenBlas让R的矩阵计算加速

1. OpenBlas介绍

2. R和OpenBlas的安装

3. 让R语言加速

Posted:

Tags:

Comments:

PageRank算法并行实现

1. PageRank算法分步式原理

2. MapReduce分步式编程

Posted:

Tags:

Comments:

用MapReduce实现矩阵乘法

1. 矩阵介绍

2. 矩阵乘法的R语言计算

3. 矩阵乘法的MapReduce计算

4. 稀疏矩阵乘法的MapReduce计算

站内导航

最新文章

最新评论

最热文章